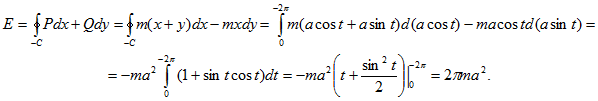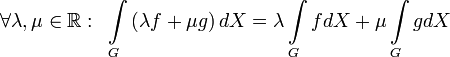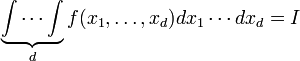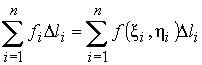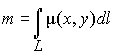Приложения криволинейных интегралов
Краткая теория
Длина дуги
Длину дуги
плоской или пространственной линии
определяют по формуле:
Масса дуги
Если
– линейная плотность вещества в точках дуги,
то массу
дуги
определяют по формуле:
Статистические моменты
Статистические
моменты
и
плоской дуги
относительно координатных осей
и
определяют по формулам:
Моменты инерции
Моменты
инерции
,
плоской дуги
относительно координатных осей
и
определяют по формулам:
Полярный момент инерции
Полярный
момент инерции
плоской дуги
относительно начала координат определяют по
формуле:
Площадь фигуры
Площадь
фигуры, расположенной в плоскости
и ограниченной замкнутой линией
, вычисляют по формуле:
Работа, приложенная к точке, при перемещении по дуге
Работу, совершаемую силой
приложенной в точке
при перемещении ее по дуге
, вычисляют по формуле:
Примеры решения задач
Задача 1
Найти
момент инерции относительно оси
четверти однородной окружности
, расположенной в первом
квадранте.
Решение
Окружность
однородна, следовательно
, следовательно искомый
момент инерции:
Для
удобства вычислений перейдем к параметрическим уравнениям окружности
Тогда:
Ответ:
Задача 2
Найти
массу дуги кривой
от точки
до
, если плотность в каждой точке
ее равна абсциссе точки;
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Плотность
дуги:
Искомая масса будет выражаться
криволинейным интегралом 1-го рода:
Производная:
Искомая масса:
Ответ:
.
Задача 3
Найти
массу дуги окружности
, лежащей в первой
четверти, если плотность в каждой ее точке равна абсциссе точки.
Решение
Плотность:
Искомая масса будет
выражаться криволинейным интегралом 1-го рода:
Параметрическое
уравнение окружности:
Окружность лежит в
первой четверти, поэтому
Ответ:
.
Задача 4
Вычислить
работу силы
при обходе точки ее приложения по границе
области
в положительном направлении, начиная от точки
.
Решение
Искомая
работа будет равна криволинейному интегралу 2-го рода:
Для
вычисления интеграла воспользуемся формулой Грина:
Ответ:
.
Задача 5
Вычислить
работу силового поля
при перемещении материальной точки вдоль пути
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Параметр
:
Перейдем к
определенному интегралу:
Искомая работа:
Ответ:
Задача 6
Вычислить
работу силы
при перемещении материальной точки вдоль линии
от точки
до точки
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Криволинейный
интеграл 2-го рода можно свести к определенному интегралу по следующей формуле:
Получаем:
Ответ:
Рабчук Александр Викторович1, Самигуллина Ракия Гареевна2
1Уфимский государственный авиационный технический университет, к.т.н.. доцент кафедры математики
2Уфимский государственный авиационный технический университет, старший преподаватель каф. математики
Аннотация
Традиционно, такие разделы высшей математики как криволинейные и поверхностные интегралы, особенно их применение, вызывают затруднения у студентов при изучении. Поэтому в данной статье кратко дана теория и приведено много разобранных примеров взятых из различных источников, в частности из [1,2,3].
Rabchuk Aleksandr Viktorovich1, Samigullina Rakiya Gareevna2
1Ufa State Aviation Technical University, PhD in Technical Science, Assistant Professor of the Mathematic Department
2Ufa State Aviation Technical University, Senior teacher of the Mathematic Department
Abstract
By tradition, devides higher mathematics by contour and surface integrals ,particularly application, is difficult by students.Therefor in this article give theori and many look into examples from [1,2,3].
Библиографическая ссылка на статью:
Рабчук А.В., Самигуллина Р.Г. Приложения криволинейных интегралов. Часть 1 // Современная педагогика. 2014. № 10 [Электронный ресурс]. URL: https://pedagogika.snauka.ru/2014/10/2675 (дата обращения: 24.02.2023).
Приложения криволинейного интеграла первого рода
1. Если подынтегральная функция равна единиц, то криволинейный интеграл
равен длине S кривой L, т.е.
2. Пусть в плоскости Оху задана гладкая кривая L, на которой определена и непрерывна функция двух переменных z=f(x,y)≥0. Тогда можно построить цилиндрическую поверхность с направляющей L и образующей, параллельной оси Оz и заключенной между L и поверхностью z=f(x,y). Площадь этой цилиндрической поверхности можно вычислить по формуле
3. Если L=AB – материальная кривая с плотностью, равной ρ=ρ(х,у), то масса этой кривой вычисляется по формуле
(физический смысл криволинейного интеграла первого рода).
4. Статистические моменты материальной кривой L относительно координатных осей Ох и Оу соответственно равны
где ρ(х,у) – плотность распределения кривой L а
— координаты центра тяжести (центра масс) кривой L.
5. Интегралы
выражают моменты инерции кривой L с линейной плотностью ρ(х,у) относительно осей Ох, Оу и начала координат соответственно.
ПРИМЕРЫ:1. Вычислить криволинейный интеграл
где L – дуга параболы у2 = 2х, заключенная между точками (2, 2) и (8, 4).
Найдем дифференциал дуги dl для кривой
. Имеем
Следовательно, данный интеграл равен
Ответ:
2. Вычислить криволинейный интеграл
где L – контур треугольника АВО с вершинами А(1,0), В(0,1), О(0,0)
Поскольку
то остается вычислить криволинейный интеграл по каждому из отрезков АВ, ВО и ОА :
1) (АВ): так как уравнение прямой АВ имеет вид у=1 – х, то . Отсюда, учитывая, что х меняется от 0 до 1, получим
2) (ВО): рассуждая аналогично, находим х=0, 0 ≤ у ≤ 1, откуда
3) (ОА):
.
4) Окончательно
Ответ:
3. Вычислить криволинейный интеграл
где L – окружность
Введем полярные координаты
Тогда, поскольку
уравнение окружности примет вид
т.е.
а дифференциал дуги
При этом Следовательно,
Ответ:
4. Вычислить криволинейный интеграл первого рода от функции с тремя переменными
где L – дуга кривой, заданной параметрически
Перейдем в подынтегральном выражении к переменной t. Имеем для подынтегральной функции:
Теперь выразим через t дифференциал dl:
Таким образом,
Ответ:
5. Вычислить площадь части боковой поверхности кругового цилиндра , ограниченной снизу плоскостью Оху, а сверху поверхностью
Искомая площадь вычисляется по формуле
где L – окружность x2+y2=R2. Поверхность цилиндра и поверхность симметричны относительно координатных плоскостей Оxz и Oyz, поэтому можно ограничиться вычислением интеграла при условиях у≥0, х≥0, т.е. вычислить четверть искомой площади и результат умножить на 4. Имеем
Следовательно,
Получили определенный интеграл, который берем подстановкой
откуда
Ответ:
6. Найти массу четверти эллипса
расположенной в первой четверти, если линейная плотность в каждой точке пропорциональна ординате этой точки с коэффициентом k.
Поскольку р(х, у)=ky, имеем
L – четверть эллипса
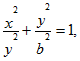
Переходим к параметрическим координатам эллипса Напомним, что
— фокусное расстояние эллипса, а
— эксцентриситет эллипса. Находим
Переходим к вычислению массы
Воспользуемся формулой
где Получаем
Учитывая, что 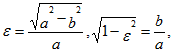
Ответ: .gif)
7. Найти координаты центра тяжести дуги окружности x2+y2=R2(0≤ x ≤R, 0≤ y ≤R).
Так как по условию задана четверть дуги окружности, то ее длина
В силу того, что биссектриса I координатного угла является осью симметрии, имеем
. Теперь находим
Ответ:
Приложения криволинейного интеграла второго рода
Интеграл
можно представить в виде скалярного произведения векторов F=Pi+Qi и ds=idx+jdy:
В таком случае
Выражает работу переменной силы F=Pi+Qj при перемещении материальной точки М=М(х,у) вдоль кривой L=AB от точки А до точки В.
При А=В кривая L замкнута, а соответствующий криволинейный интеграл по замкнутой кривой обозначается так:
В этом случае направление обхода контура иногда поясняется стрелкой на кружке, расположенном на знаке интеграла.
Предположим, что в плоскости Оху имеется односвязная область D (это значит, что в ней нет «дыр»), ограниченная кривой , (
— обозначение границы области D), а в области D и на ее границе
функции Р(х,у) и Q(х,у) непрерывны вместе со своими частными производными.
Теорема: Пусть А и В – произвольные точки области D, AmB и AnB – два произвольных пути (гладкие кривые), соединяющие эти точки (рис. 2).
Тогда следующие условия равносильны:
1. (условие Грина).
2. (криволинейный интеграл не зависит от пути интегрирования).
3. (интеграл по любому замкнутому пути равен нулю).
4. (выражение
представляет собой полный дифференциал некоторой функции
).
В случае выполнения любого из равносильных условий предыдущей теоремы криволинейный интеграл по любой кривой, соединяющей точки (хо, уо) и (х1, у1) из области D, можно вычислить при помощи формулы Ньютона-Лейбница
где U(x, y) – некоторая первообразная для P dx + Q dy.
С другой стороны, первообразная U(x, y) выражения P dx + Q dy может быть найдена при помощи криволинейного интеграла
В этих же условиях на функции Р(х,у) и Q(х,у), а также на область D, имеет место формула Грина, позволяющая свести криволинейный интеграл по замкнутому контуру к двойному интегралу
Здесь предполагается, что обход границы области D в криволинейном интеграле
совершается в положительном направлении, т.е. при таком обходе границы область D остается слева; для односвязной области это направление совпадает с направлением против часовой стрелки.
Заметим, что площадь S=S(D) области D может быть вычислена при помощи криволинейного интеграла второговрода:
(эта формула получается из формулы Грина с ).
ПРИМЕРЫ:1. Даны функции Р(х ,у) = 8х+4у+2, Q(х ,у) = 8у+2 и точки А(3, 6), В(3,0), С(0,6). Вычислить криволинейный интеграл
где:
1) L – отрезок ОА;
2) L – ломаная ОВА;
3) L – ломаная ОСА;
4) L – парабола, симметричная относительно оси Оу и проходящая через точки О и А;
5) проверить выполнимость условия Грина.
1) Отрезок ОА может быть записан в виде: у=2х, . Тогда dy=2dx и
2) Используем свойство аддитивности, вычисляя отдельно интеграл по отрезкам ОВ и ВА. Тогда:
а) ОВ: здесь у=0, 0≤х≤3, т.е. dy=0, откуда
б) ВА: х=3, 0≤у≤6, т.е. dx=0, и
Таким образом,
3) Этот интеграл вычислим аналогично предыдущему.
а) ОС: х=0, (т.е. dx=0), 0≤y≤6, откуда
б) СА: 0≤х≤3 , у=6, dy=0, следовательно,
Окончательно
4) Подставив координаты точки А(3;6) в равенство у=ах2 найдем уравнение данной параболы . При этом 0≤х≤3 и
откуда (путь ОА по параболе обозначим
)
5) Имеем
т.е. условие Грина не выполняется. Этот факт, а также вычисления в пунктах 1) – 4) этой задачи показывают, что данный криволинейный интеграл второго рода зависит от пути интегрирования.
2. Вычислить интеграл
где L – верхняя половина эллипса .gif)
Воспользуемся параметрическими уравнениями эллипса: х=a cost, y=b sin t,
т.е. dx = – a sin t dt, dy = b cos t dt. Подставляя в интеграл и учитывая направление обхода (откуда следует, что t меняется от π до 0), получаем
.gif)
3. Вычислить криволинейный интеграл
где L – отрезок, соединяющий точку С(2, 3, -1) с точкой D(3, -2, 0).
Составим параметрические уравнения отрезка СD, используя уравнения прямой, проходящей через две точки:
Отсюда . Далее, находим
подставляем все нужные выражения в данный интеграл, обозначенный через J, и вычисляем определенный интеграл:
Ответ:
4. Вычислить где К – отрезок прямой от А(0 ;0) до В (4; 3).
Уравнение прямой АВ имеет вид у=(3; 4)х. Находим у/= ¾ и, следовательно,
Ответ:
5. Вычислить если
Найдем
Тогда
Ответ:
6. Найти массу М дуги кривой x=t, y=t2/2, z=t3/3 (0≤ t ≤1), линейная плотность которой меняется по закону
Ответ:
7. Вычислить криволинейный интеграл от точки А(1, 0) до точки В(0, 2) (рис. 3):
1) по прямой 2х+у=2;
2) по дуге параболы 4х+у2=4;
3) по дуге эллипса x=cost, y=2sint.
1) Пользуясь данным уравнением линии интегрирования, преобразуем криволинейный интеграл в обыкновенный определенный интеграл с переменной х, затем вычисляем его:
у=2-2х, dy=-2dx,
2) Здесь удобно преобразовать криволинейный интеграл в обыкновенный интеграл с переменной у:
3) Преобразуем данный интеграл в обыкновенный с переменной t, затем вычисляем его: x=cost, dx=-sintdt; y=2sint; dy=2costdt:
Ответ: I1=1, I2=-1/5, I3=4/3.
8. Вычислить криволинейный интеграл между точками Е
(-1, 0) и Н (0, 1):
1) по прямой ЕН;
2) по дуге астроиды х=cos3t, y=sin3t.
1) Вначале составляем уравнение линии интегрирования – прямой ЕН, как уравнение прямой, проходящей через две известные точки: у-х=1.
Пользуясь этим уравнением и известной формулой для дифференциала дуги плоской кривой преобразуем данный криволинейный интеграл в обыкновенный интеграл с переменной х и вычисляем его:
2) Преобразуем данный интеграл в обыкновенный с переменной t, затем вычисляем:
ибо π/2≤ t ≤π;
Ответ:
9. Даны точки А(3, -6, 0) и В(-2, 4, 5). Вычислить криволинейный интеграл
1) по прямолинейному отрезку ОВ;
2) по дуге АВ окружности, заданной уравнениями x2+y2+z2=45, 2x+y=0.
1) Вначале составляем уравнения линии интегрирования – прямой ОВ.
Пользуясь общими уравнениями прямой, проходящей через две точки .gif)
Приравнивая эти равные отношения параметру t, преобразуем полученные канонические уравнения прямой ОВ к параметрическому виду: x=-2t, y=4t, z=5t.
Далее, пользуясь этими уравнениями, преобразуем данный криволинейный интеграл в обыкновенный интеграл с переменной t, затем вычисляем его
2) Преобразуем данные уравнения окружности к параметрическому виду. Полагая х=t, получим у=-2t (из второго данного уравнения), (из первого уравнения). Отсюда
.gif)
Ответ:
10. Вычислить криволинейные интегралы:
1)
2) вдоль периметра треугольника с
вершинами А(-1,0), В (0,2) и С (2,0)
Составив уравнение прямой АВ, у-2х=2, и исходя из этого уравнения, преобразуем криволинейный интеграл на отрезке АВ в обыкновенный интеграл с переменной х:
у=2х+2, dy=2dx,
Аналогичным путем вычисляя криволинейный интеграл на отрезках ВС и СА, получим
х=2-у, dx=-dy,
Следовательно,
2) Здесь подынтегральное выражение есть полный дифференциал функции двух переменных, ибо (уcosx)’y =(sinx)’x =cosx. Вследствии этого данный криволинейный интеграл, взятый по периметру данного треугольника равен нулю. Он будет равен нулю и по любому другому замкнутому контуру.
Ответ:
11. Найти длину кардиоиды x=2acost-acos2t, y=2asint-asin2t.
Применяем формулу
, исходя из данных параметрических уравнений кардиоиды и формулы для дифференциала дуги плоской кривой, преобразуем криволинейный интеграл формулы в обыкновенный интеграл с переменной t.
Ответ: L=16a.
12. Найти площадь, ограниченную замкнутой кривой:
1) эллипсом x=a cost, y=b sint;
2) петлей декартова листа х3+у3-3аху=0.
1) Применяем формулу
, исходя из данных параметрических уравнений эллипса, преобразуем криволинейный интеграл в обыкновенный интеграл с переменной t и вычисляем его:
2) Вначале преобразуем данное уравнение к параметрическому виду. Полагая у=хt, получим
Геометрический параметр t=y/x есть угловой коэффициент полярного радиуса ОМ (рис. 6), точка М(х, у) опишет всю петлю кривой при изменении t от 0 до +∞.
Преобразуя криволинейный интеграл формулы в обыкновенный интеграл с переменной t , получим
Ответ: S=3a2/2.
13. Найти массу дуги АВ кривой у=lnx, если в каждой ее точке линейная плотность пропорциональна квадрату абсциссы точки: хА=1, хВ=3.
Применяем формулу
, исходя из данного уравнения кривой, преобразуем криволинейный интеграл в обыкновенный с переменной х
Ответ:
14. Найти координаты центра тяжести дуги АВ винтовой линии х=аcost, y=asint, z=bt, если в каждой ее точке линейная плотность пропорциональна аппликате этой точки: tA=0, tB=π.
Применяя формулы
.gif)
Следовательно,
Ответ:
15. Вычислить работу, совершаемую силой тяжести при перемещении точки массы m по дуге АВ некоторой кривой.
Если выбрать прямоугольную систему координат так, чтобы направление оси Оz совпало с направлением силы тяжести, то действующая на точку сила
а ее проекции на оси координат Fx=P=O, Fy=Q=0, Fz=R=mg.
Искомая работа согласно формуле
Она зависит только от разности аппликат начала и конца пути, но не зависит от формы пути.
16. Найти работу силового поля, в каждой точке (х,у) которого напряжение (сила, действующая на единицу массы) , когда точка массы m описывает окружность x=accost, y=asint, двигаясь по ходу часовой стрелки.
Подставляя в формулу
проекции силы
действующей на точку: Fx=m(x+y), Fy= – mx, и преобразуя криволинейный интеграл в обыкновенный с переменной t, получим
Ответ: Е=2πma2.
Библиографический список
- Лунгу К.Н. Сборник задач по высшей математике. 1 курс – 7-е изд., – М.: Айрис-пресс, 2008.
- Лунгу К.Н. Сборник задач по высшей математике. 2 курс – 5-е изд., – М.: Айрис-пресс, 2007.
- Письменный Д.Т. Конспект лекций по высшей математике: полный курс – 7-е изд. – М.: Айрис-пресс, 2008.
Все статьи автора «Рабчук Александр Викторович»
Соберем в одном месте все формулы.
Масса [math]m[/math] гладкой кривой[math]L[/math], линейная плотность которой вдоль кривой [math]L[/math] равна [math]gamma(x,y,z)[/math], выражается криволинейным интегралом первого рода:
[math]m=int_{L}gamma(x,y,z);dl[/math]
Криволинейный интеграл равен обычному и совсем не опасному интегралу функции одной переменной 
* Если кривая задана параметрическими уравнениями [math]x=x(t), y=y(t), z=z(t),hspace{2mm}tin[alpha,beta][/math], то
[math]m=int_{alpha}^{beta}gamma(x(t),y(t),z(t))sqrt{x'(t)^2+y'(t)^2+z'(t)^2)};dthspace{10mm}(1)[/math]
* Если кривая лежит в плоскости [math]Oxy[/math], то [math]z(t)=0[/math] и получаем
[math]m=int_{alpha}^{beta}gamma(x(t),y(t))sqrt{x'(t)^2+y'(t)^2};dthspace{37mm}(2)[/math]
В частности, для плоской кривой, заданной уравнением [math]y=f(x), xin[a,b][/math] имеем
[math]m=int_{a}^{b}gamma(x,f(x))sqrt{1+f'(x)^2};dxhspace{47mm}(3)[/math]
* Если плоская кривая задана уравнением [math]rho=rho(phi}), hspace{3mm}phiin[alpha,beta][/math] в полярных координатах, то
[math]m=int_{alpha}^{beta}gamma(rhocosphi,rhosinphi)sqrt{rho^2+rho ‘^2};dphihspace{45mm}(4)[/math]
————————————————————————
В данной задаче надо применить формулу (3):
[math]gamma(x,y)=frac{2sqrt x-y}{sqrt{1+frac{1}{x}}},hspace{3mm}y=f(x)=2sqrt x-1, hspace{3mm}xin [0,4][/math]
[math]gamma(x,f(x))=frac{2sqrt x -(2sqrt x-1)}{sqrt{1+frac{1}{x}}}=frac{1}{{sqrt{1+frac{1}{x}}}[/math]
Так как
[math]f'(x)=frac{1}{sqrt x}[/math]
то
[math]sqrt{1+f'(x)^2}=sqrt{1+frac{1}{x}}[/math]
И получаем миленький интегральчик.
Предположим,
что кусок проволоки описывается некоторой
пространственной кривой C.
Пусть масса распределена вдоль этой
кривой с плотностью ρ (x,y,z).
Тогда общая масса
кривой выражается
через криволинейный интеграл первого
рода
Если
кривая C задана
в параметрическом виде с помощью
векторной функции
,
то ее масса описывается формулой
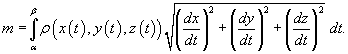
В
случае плоской кривой, заданной в
плоскости Oxy,
масса определяется как
или
в параметрической форме
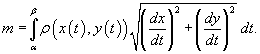
2.16
понятие момента фиксированного порядка
n>1, n=1
и соответствующегося ему центра у массы
вдоль кривой.
Центр
масс и моменты инерции кривой
Пусть
снова кусок проволоки описывается
некоторой кривой C,
а распределение массы вдоль кривой
задано непрерывной функцией
плотности ρ (x,y,z).
Тогда координаты
центра масс кривой определяются
формулами
где
−
так
называемые моменты
первого порядка.
Моменты
инерции относительно осей Ox, Oy и
Oz определяются
формулами
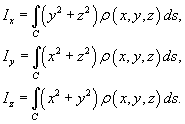
3.Вопросы потеме «кратные интыгралы»
3.2 Свойство аддитивности кратного интеграла
-
Аддитивность
по множеству интегрирования. Пусть
множества G1 и
G2 измеримы,
и
.
Пусть также функция f определена и
интегрируема на каждом из множеств
G1 и
G2.
Тогда интеграл по G существует и равен
.
.3.3. свойство
линейности для кратного интеграла
Линейность
по функции.
Пусть
измеримо,
функции
и
интегрируемы
на
,
тогда
.
3.4.Сведенья кратного интеграла к интегралам одной переменной.
Кратным
(n-кратным) интегралом функции
на
множестве
называется число
(если
оно существует), такое что, какой бы
малой
-окрестностью
числа
мы
ни задались, всегда найдется такое
разбиение множества
и
набор промежуточных точек, что сумма
произведений значения функции в
промежуточной точке разбиения на меру
разбиения будет попадать в эту окрестность.
Формально:
:
: 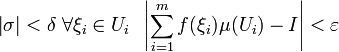
Здесь
—
мера множества
.
Это
определение можно сформулировать в
другой форме с использованием интегральных
сумм. А именно, для данного разбиения
и
множества точек
рассмотрим
интегральную сумму
Кратным
интегралом функции
называют
предел
если
он существует. Предел берётся по множеству
всех последовательностей разбиений, с
мелкостью стремящейся к 0. Разумеется,
это определение отличается от предыдущего,
по сути, лишь используемым языком.
Интеграл
обозначается следующим образом:
-
В
векторном виде:
, -
Либо
ставят значок интеграла
раз,
записывают функцию и
дифференциалов:
. -
Для
двойного и тройного интегралов
используются также
обозначения
и
соответственно.
В
современных математических и физических
статьях многократное использование
знака интеграла не применяется.
Такой
кратный интеграл называется интегралом
в собственном смысле.
4.1 два
типа криволинейногоинтеграла
Криволинейный интеграл первого типа (по длине дуги)
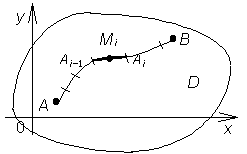
Пусть
в некоторой области D плоскости хоу (см.
рис. 1) задана непрерывная функция f(x,
y)
и гладкая незамкнутая кривая L между
точками А, В.
Рис.
1
Составим
интегральную сумму по уже известному
алгоритму. Разобьём кривую L точками
А = А0, А1,
…, Ап = В
на п произвольных
участков li, обозначив
через
длину i-го
участка кривой между точками Аi-1, Ai,
где I =
1, 2, …,п.
В
каждом i-том
участке выберем произвольно точку
и
подсчитаем в ней значение функции fi = f(Mi).
Просуммировав
произведения
по
всем i =
1, 2, …, п,
получим интегральную сумму
.
Предел
этой интегральной суммы, если он
существует и не зависит от типа разбиения
дуги L и
способа нахождения точек Mi, где i =
1, 2, …, п,
называется криволинейным интегралом первого типа от функции f(x,
y),
взятым по кривой L,
и обозначается
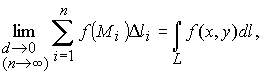
где
.
Этому
интегралу можно придать вполне
определённый физический смысл: если в
каждой точке дуги L задана
переменная плотность
—
функция точки, то можно подсчитать массу
материальной дуги АВ:
.
(1)
Сравните
с задачей о вычислении массы неоднородного
стержня, приводящей к понятию определённого
интеграла .
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пусть: 1) в точках простой (без точек самопересечения), спрямляемой (т. е. имеющей длину) кривой L из пространства определена ограниченная скалярная функция
2)
— произвольное разбиение кривой L на элементарные дуги
с длинами
; 3)
— произвольный набор точек; 4)

.
Определение. Конечный предел интегральной суммы при
, не зависящий ни от способа разбиения кривой L, ни от выбора точек
, называется Криволинейным интегралом первого рода от функции
по кривой L:
.
Вычисление КИ-1. Теорема 14.6. Если кривая l задана параметрическими уравнениями: , где
— непрерывно дифференцируемые по T функции и возрастание длины L дуги кривой соответствует возрастанию T, то в предположении существования определенного интеграла имеет место равенство

Следствия.
А) Если плоская кривая L задана Явно: , и
, то

Б) Если плоская кривая L задана в Полярных координатах: , то

Некоторые приложения КИ-1
1. Масса материальной линии. Пусть ,
— линейная плотность массы материальной линии l. Тогда масса этой линии есть:
. (5.4)
2. Длина пространственной (или плоской) кривой L есть L: .
3. Статические моменты и координаты центра тяжести.
а) Для Плоской линии c плотностью
и массой M статические моменты относительно координатных осей Oy и Ox:
,
;
Координаты центра тяжести:
,
.
Б) Для Пространственной линии L c плотностью и массой M статические моменты относительно плоскостей
и Oxy:
,
,
;
координаты центра тяжести:
,
,
.
Пример 17. Вычислить КИ-1: , где L – прямолинейный отрезок, соединяющий точки
и
.
Ñ Уравнения отрезка прямой AB в параметрической форме: 
или
. Тогда
и из (5.1) имеем
=.
Замечание. В случае явного задания отрезка прямой
следует воспользоваться формулой (5.2). #
Пример 18. Вычислить КИ-1: 
при условии
.
Ñ Для построения кривой L преобразуем уравнение ее к виду ; таким образом, L есть полуокружность с центром в точке
радиуса 1, расположенная слева от оси Oy (рис. 14.22).
Наличие комбинации в подынтегральной функции и в уравнении L наводит на мысль провести вычисления в полярных координатах, которые связаны с декартовыми координатами формулами
. Тогда: из
Рис. 14.22
получаем
– уравнение L в полярных координатах; из рис. 14.22 (или условий
,
,
следует:
;
,
= =
=
, и из (5.3)


. #
Пример 19. Найти массу одного витка материальной винтовой линии ,
,
(рис. 14.23),
Если линейная плотность в точке обратно пропорциональна квадрату расстояния этой точки от начала координат.
Ñ По условию задачи плотность +
=
, где K – коэффициент про-
Порциональности,
. Для одного витка
. Из формул (5.4) и (5.1) имеем:
=

. #
Задачи для самостоятельного решения
Вычислить криволинейные интегралы первого рода:
81. 
, заключенный между точками
и
.
82. , где L – контур прямоугольника с вершинами:
.
83. , где L – дуга параболы
, отсеченная параболой
.
84. , где L – первая арка циклоиды
.
85. , где L— половина лемнискаты
.
86. 
, заключенная внутри круга радиуса R с центром в точке
.
87. , где L – первый виток конической винтовой линии
,
,
.
88. , где L –четверть окружности
, лежащая в первом октанте.
89. , где L – дуга гиперболы
,
.
90. , где L – дуга астроиды
в первом квадранте.
91. Найти массу первого витка винтовой линии , плотность которой в каждой точке равна полярному радиусу этой точки.
92. Найти массу линии ,
, от точки, соответствующей T=0, до произвольной точки, если плотность в каждой точке обратно пропорциональна квадрату полярного радиуса и в точке
Равна единице.
93. Найти массу дуги параболы , если линейная плотность в текущей точке равна
.
Вычислить координаты центра тяжести дуги однородной кривой :
94. , от точки
До точки
.
95. .
96. .
| < Предыдущая | Следующая > |
|---|

.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
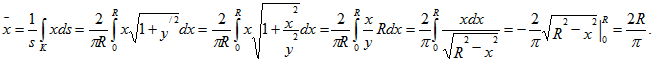
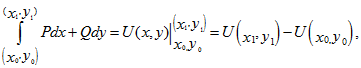
.gif)
.gif)
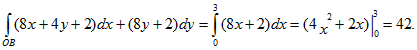
.gif)
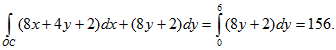
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
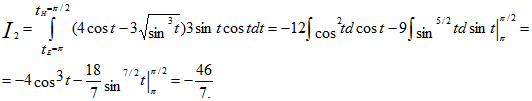
.gif)
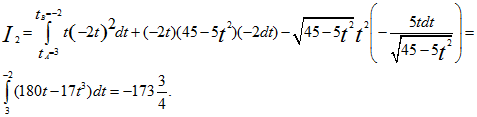
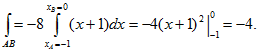
.gif)
.gif)
.gif)
.gif)
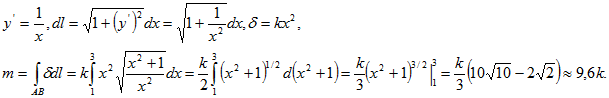
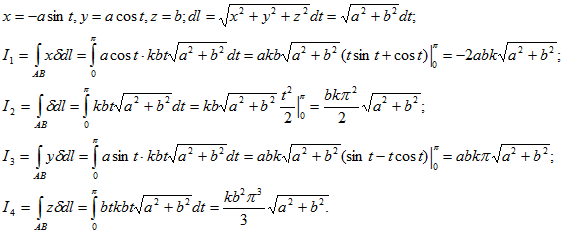
.gif)