Как найти массу фотона монохроматического света

Формула для массы фотона

(4.17)

Масса
фотона существенно отличается от массы
макроскопических тел и масс других
«элементарных» частиц. Это отличие
состоит в том, что фотон не обладает
массой покоя

.

Импульс
фотона является векторной величиной.
Направление импульса совпадает с
направлением распространения света,
харак­теризуемым волновым вектором

,
который численно равен волновому числу.
Следовательно,

(4.18)

где

Таким
образом, фотон, подобно любой движущейся
частице или телу, обладает энергией,
массой и импульсом. Все эти три
корпу­скулярные характеристики фотона
связаны с волновой характеристикой
света — его частотой v.

Квантовые свойства
света проявляются в явлении, которое
обнаружил А. Комптон (1923), наблюдая
рассеяние монохро­матических
рентгеновских лучей «легкими» веществами
(графит, парафин и др.). Схема эксперимента
Комптона изображена на рис. 4.5.

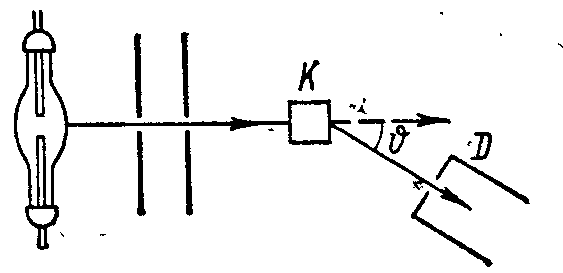
Рис. 4.5.

Схема эксперимента
Комптона

Узкий
диафрагмированный пучок монохроматических
рентгеновских лучей падает на «легкое»
рассеивающее вещество К
и после рассеяния на угол

попадает в приемник — рентгеновский
спектрограф D,
где измеряется длина волны рассеянного
излучения.

Эксперименты
Комптона показали, что длина волны ‘
рассеянного из­лучения больше длины
волны 
падающего излучения, причем раз­ность
‘
— 
зависит
только от угла рассеяния

:

(4.19)

где

— так называемая
комптоновская длина волны.
Это явление получило название
эффекта Комптона.

ВОПРОСЫ ДЛЯ
САМОПОДГОТОВКИ

4.1. Определение
теплового излучения.

4.2. Определение
испускательной способности тела.

4.3. Определение
поглощательной способности тела.

4.4. Определение
абсолютно черного тела.

4.5. Определение
спектральной плотности энергии черного
излучения.

4.6. Закон Кирхгофа
в дифференциальной форме.

4.7. Определение
абсолютно черного тела.

4.8. Определение
энергетической светимости тела.

4.9. Закон Кирхгофа
в интегральной форме для серых тел.

4.10. Закон Стефана
– Больцмана.

4.11. Закон смещения
Вина.

4.12. Формула Релея
– Джинса.

4.13. Определение
фотона.

4.14. Формула Планка.

4.15. Определение
фототока.

4.16. Определение
внешнего фотоэффекта.

4.17. Определение
фотоионизации.

4.18. Определение
фототока насыщения.

4.19. Определение
квантов электромагнитного излучения.

4.20. Законы внешнего
фотоэффекта.

4.21. Красная граница
фотоэффекта.

4.22. Уравнение
Эйнштейна для фотоэффекта.

4.23. Определение
внутреннего фотоэффекта.

4.24. Определение
вентильного фотоэффекта.

4.25. Формула для
массы фотона.

4.26. Формула импульса
фотона.

4.27. Эффект Комптона.

4.28. Комптоновская
длина волны.

4.29. Правило Прево.

АЛГОРИТМ
РЕШЕНИЯ ЗАДАЧ ПО ТЕМЕ: «ТЕПЛОВОЕ
ИЗЛУЧЕНИЕ. ФОТОЭФФЕКТ»

1. Записать формулы,
позволяющие определить неизвестную
физическую величину.

2. Решить полученную
систему уравнений относительно искомой
величины.

3. Проверить единицы
физических величин измерений справа и
слева от знака равенство.

ПРИМЕРЫ РЕШЕНИЯ
ЗАДАЧ ПО ТЕМЕ: «ТЕПЛОВОЕ ИЗЛУЧЕНИЕ.
ФОТОЭФФЕКТ»

Задача
4.1. Длина
волны, на которую приходится максимум
энергии в спектре излучения черного
тела,

= 0,58 мкм. Определить энергетическую
светимость (излучательность)

поверхности тела.

Дано: = 0,58 мкм

Найти: — ?

1. Согласно уравнениям
(4.9) и (4.10), имеем:

(1) (2)

2.
Подставив (2) в (1), можно получить:

(3)

3.
Вычисления производим в Международной
системе единиц СИ:

.

Ответ:

= 35,4

.

Задача
4.2. В результате
эффекта Комптона фотон при соударении
с электроном был рассеян на угол

.
Энергия рассеянного фотона

= 0,4 МэВ. Определить энергию фотона

до рассеяния.

Дано: = 0,4 МэВ

Найти: — ?

1.
Согласно уравнению (4.19), можно получить:

(1)

где

— изменение длины волны фотона в результате
рассеяния на свободном электроне; h
– постоянная
Планка;

— масса покоя электрона; с
– скорость света вакууме; θ
– угол рассеяния фотона.

Согласно
уравнению (4.14), имеем:

(2)

Решая
систему уравнений, имеем:

(3)

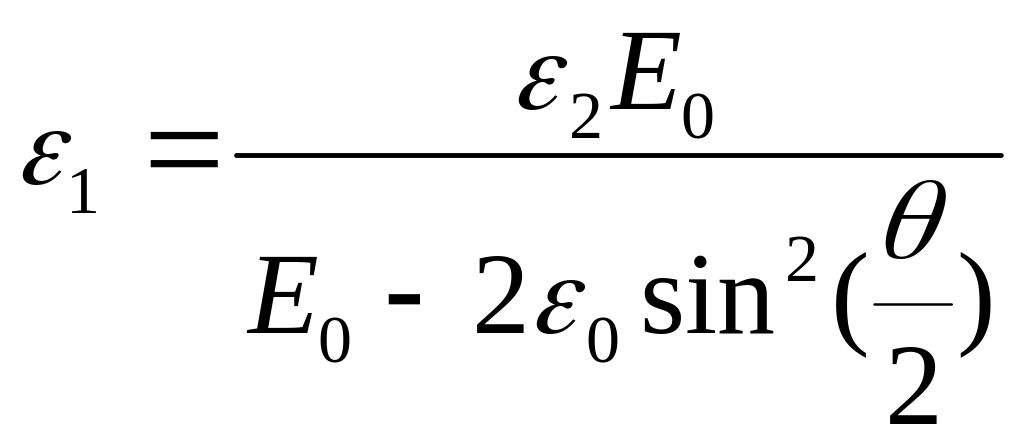
Вычисления
производим в Международной системе
единиц СИ:

МэВ.

Ответ:

= 1,85 МэВ.

ЗАДАЧИ
ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

4.1.
Определить
импульс р
и кинетическую энергию Т
электрона, движущегося со скоростью υ
= 0,9 с, где с
скорость света в вакууме.

(Ответ:
p
=

;
Т
=

Дж)

4.2.
Пучок монохроматического света с длиной
волны λ
= 663 нм падает нормально на зеркальную
плоскую поверхность. Поток излучения

=
0,6 Вт. Определить: 1) силу давления F,
испытываемую этой поверхностью; 2) число
фотонов ежесекундно падает на поверхность.

(Ответ:
F
= 4 нН;

)

4.3.
Импульс,
переносимый монохроматическим пучком
фотонов через площадку S
= 2

за
время t
= 0,5 мин равен р
=

.
Найти для этого пучка энергию Е,
падающих на единицу площади за единицу
времени.

(Ответ:
Е
= 150

)

4.4.
Какую
энергетическую светимость

имеет абсолютно черное тело, если
максимум спектральной плотности его
энергетической светимости приходится
на длину волны λ
= 484 нм.

(Ответ:

= 73,08 М
)

4.5.
Абсолютно
черное тело
имеет
температуру

= 2900 К. В результате остывания тела длина
волны, на которую приходится максимум
спектральной плотности энергетической
светимости, изменилась на Δλ
= 9 мкм. До какой температуры

охладилось тело.

(Ответ:

= 290 К)

4.6.
В работе
А.Г. Столетова «Активно – электрические
исследования» (1888 г.) впервые были
установлены основные законы фотоэффекта.
Один из результатов его экспериментов
был сформулирован так: «Разряжающим
действием обладают лучи самой высокой
преломляемости с длиной волны менее
295 нм». Найти работу выхода А
электрона из металла, с которым работал
А.Г. Столетов.

(Ответ:
А =
4,2 эВ)

4.7.
Длина волны
света, соответствующая красной границе
фотоэффекта, для некоторого металла

= 275 нм. Найти работу выхода А
электрона из металла, максимальную
скорость

электронов, вырываемых из металла светом
с длиной волны λ
= 180 нм, и максимальную кинетическую
энергию

электронов.

(Ответ:

4.8.
В каких областях спектра лежат длины
волн, соответствующие максимуму
спектральной плотности энергетической
светимости, если источником света
служит: а) спираль электрической лампочки
(Т
= 3000 К); б) поверхность Солнца (Т
= 6000 К); в) атомная бомба, в которой в
момент взрыва развивается температура

К. Излучение считать близким к излучению
абсолютно черного тела.

(Ответа:
а)

= 1,03 мкм; б)

=
483 нм; в)

пм)

4.9.
Внутренняя
корона Солнца (называемая К
– короной) представляет собственно
солнечный свет, рассеянный свободными
электронами. Кажущаяся яркость этой К
– короны на расстоянии одного солнечного
радиуса от солнечного диска составляет
около

от яркости самого диска (на единицу
площади). Вычислите число свободных
электронов в 1

пространства вблизи Солнца.

(Ответ:

)

4.10.
Межзвездное пространство заполнено
облаками из крошечных пылинок, состоящих
из углерода, льда и очень малого количества
других элементов. Какова должна быть
минимальная масса таких пылинок,
отнесенная к единице площади (1

),
способная ухудшить наши наблюдения за
звездами, скажем в 100 раз (т.е. на 5,0
звездной величины). Не забудьте, что
свет от звезд может не только рассеиваться
на пылинках, но и просто ими поглощаться.

(Ответ:

)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

19.1 Найти массу фотона красных лучей света (λ= 700 нм); рентгеновски лучей (25 нм); гамма-лучей (1,24 нм)
РЕШЕНИЕ

19.2 Найти энергию, массу и импульс фотона, если соответствующая ему длина волны λ = 1,6 нм
РЕШЕНИЕ

19.3 Ртутная дуга имеет мощность N = 125 Вт. Какое число фотонов испускается в единицу времени в излучении с длинами волн, равными: 612,1; 579,1; 546,1; 404,7; 365,5; 253,7 нм. Интенсивности этих линий составляют соответственно 2; 4; 4; 2,9; 2,5; 4% интенсивности ртутной дуги. Считать, что 80% мощности дуги идет на излучение
РЕШЕНИЕ

19.4 С какой скоростью должен двигаться электрон, чтобы его кинетическая энергия была равна энергии фотона с длиной волны λ = 521 нм
РЕШЕНИЕ

19.5 С какой скоростью v должен двигаться электрон, чтобы его импульс был равен импульсу фотона с длиной волны 520 нм
РЕШЕНИЕ

19.6 Какую энергию должен иметь фотон, чтобы его масса была равна массе покоя электрона
РЕШЕНИЕ

19.7 Импульс, переносимый монохроматическим пучком фотонов через площадку S = 2 см2 за время t = 0,5 мин, равен p = 3·10-9 кг·м/с. Найти для этого пучка энергию, падающую на единицу площади за единицу времени
РЕШЕНИЕ

19.8 При какой температуре кинетическая энергия молекулы двухатомного газа будет равна энергии фотона с длиной волны λ = 589 нм?
РЕШЕНИЕ

19.9 При высоких энергиях трудно осуществить условия для изменения экспозиционной дозы рентгеновского и гамма-излучений в рентгенах, поэтому допускается применение рентгена как единицы дозы для излучений с энергией квантов до e = 3 МэВ. До какой предельной длины волны рентгеновского излучения можно употреблять рентген
РЕШЕНИЕ

19.10 Найти массу фотона, импульс которого равен импульсу молекулы водорода при температуре t = 20° C. Скорость молекулы считать равной средней квадратичной
РЕШЕНИЕ

19.11 В работе Столетова Актино-электрические исследования впервые были установлены основные законы фотоэффекта. Один из результатов его опытов был сформулирован так: Разряжающим действием обладают лучи самой высокой преломляемости с длиной волны менее 295 нм . Найти работу выхода электрона из металла, с которым работал A. Г. Столетов
РЕШЕНИЕ

19.12 Найти длину волны света, соответствующую красной границе фотоэффекта, для лития, натрия, калия и цезия
РЕШЕНИЕ

19.13 Длина волны света, соответствующая красной границе фотоэффекта, для некоторого металла λ0 = 275 нм. Найти минимальную энергию фотона, вызывающего фотоэффект
РЕШЕНИЕ

19.14 Длина волны света, соответствующая красной границе фотоэффекта, для некоторого металла λ0 = 275 нм. Найти работу выхода электрона из металла, максимальную скорость электронов, вырываемых из металла светом с длиной волны λ = 180 нм, и максимальную кинетическую энергию электронов.
РЕШЕНИЕ

19.15 Найти частоту света, вырывающего из металла электроны, которые полностью задерживаются разностью потенциалов U = 3 B. Фотоэффект сжимается при частоте света λ0 = 6·10^14 Гц. Найти работу выхода электрона из металла
РЕШЕНИЕ

19.16 Найти задерживающую разность потенциалов для электронов, вырываемых при освещении калия светом с длиной волны λ= 330 нм.
РЕШЕНИЕ

19.17 При фотоэффекте с платиновой поверхности электроны полностью задерживаются разностью потенциалов U = 0,8 B. Найти длину волны применяемого облучения и предельную длину волны, при которой еще возможен фотоэффект.
РЕШЕНИЕ

19.18 Фотоны с энергией e = 4,9 эВ вырывают электроны из металла с работой выхода A = 4,5 эВ. Найти максимальный импульс, передаваемый поверхности металла при вылете каждого электрона.
РЕШЕНИЕ

19.19 Найти постоянную Планка h, если известно, что электроны, вырываемые из металла светом с частотой v1 = 2,2·10^5 Гц, полностью задерживаются разностью потенциалов U1 = 6,6 B, а вырываемые с частотой v2= 4,6·10^15 Гц разностью потенциалов U2 = 16,5 B
РЕШЕНИЕ

19.20 Вакуумный фотоэлемент состоит из центрального катода (вольфрамового шарика) и анода (внутренней поверхности посеребренной изнутри колбы). Контактная разность потенциалов между электродами U0 = 0,6 В ускоряет вылетающие электроны. Фотоэлемент освещается светом с длиной волны λ = 230 нм. Какую задерживающую разность потенциалов надо приложить между электродами, чтобы фототок упал до нуля? Какую скорость получат электроны, когда они долетят до анода, если не прикладывать между катодом и анодом разности потенциалов?
РЕШЕНИЕ

19.21 Между электродами фотоэлемента предыдущей задачи приложена задерживающая разность потенциалов U = 1 B. При какой предельной длине волны падающего на катод света начинается фотоэффект
РЕШЕНИЕ

19.22 На рисунке показана часть прибора, с которым Лебедев производил свои опыты по измерению светового давления. Стеклянная крестовина, подвешенная на тонкой нити заключена в откачанный сосуд и имеет на концах два легких кружка из платиновой фольги. Один кружок зачернен, другой оставлен блестящим. Направляя свет на один из кружков и измеряя угол поворота нити (для зеркального отсчета служит зеркальце S), можно определить световое давление. Найти световое давление P и световую энергию E , падающую от дуговой лампы в единицу времени на единицу площади кружков. При освещении блестящего кружка отклонение зайчика a = 76 мм по шкале, удаленной от зеркальца на расстояние b = 1200 мм. Диаметр кружков d = 5 мм. Расстояние от центра кружка до оси вращения l = 9,2 мм. Коэффициент отражения света от блестящего кружка ρ = 0,5. Постоянная момента кручения нити (M = k α ) k = 2,2·10-11 Н·м/рад.
РЕШЕНИЕ

19.23 В одном из опытов Лебедева при падении света на зачерненный кружок (ρ = 0) угол поворота нити был равен α = 10′. Найти световое давление и мощность падающего света. Данные прибора взять из условия задачи 19.22
РЕШЕНИЕ

19.24 В одном из опытов Лебедева мощность падающего на кружки монохроматического света (λ = 560 нм) была равна N = 8,33 мВт. Найти число фотонов I, падающих в единицу времени на единицу площади кружков, и импульс силы FΔt, сообщенный единице площади кружков за единицу времени, для значений ρ, равных: 0; 0,5; 1. Данные прибора взять из условия задачи 19.22
РЕШЕНИЕ

19.25 Русский астроном Бредихин объяснил форму кометных хвостов световым давлением солнечных лучей. Найти световое давление солнечных лучей на абсолютно черное тело, помешенное на таком же расстоянии от Солнца, как и Земля. Какую массу m должна иметь частица в кометном хвосте, помещенная на этом расстоянии, чтобы сила светового давления на нее уравновешивалась силой притяжения частицы Солнцем? Площадь частицы, отражающую все падающие на нее лучи, считать равной S = 0,5·10-12 м2. Солнечная постоянная K = 1,37 кВт/м2.
РЕШЕНИЕ

19.26 Найти световое давление на стенки электрической 100-ваттной лампы. Колба лампы представляет собой сферический сосуд радиусом r = 5 см. Стенки лампы отражают 4% и пропускают 6% падающего на них света. Считать, что вся потребляемая мощность идет на излучение.
РЕШЕНИЕ

19.27 На поверхность площадью S = 0,01 м2 в единицу времени падает световая энергия E = 1,05 Дж/с. Найти световое давление в случаях, когда поверхность полностью отражает и полностью поглощает падающие на нее лучи
РЕШЕНИЕ

19.28 Монохроматический пучок света (λ= 490 нм), падая по нормали к поверхности, производит световое давление P = 4,9 мкПа. Какое число фотонов падает в единицу времени на единицу площади этой поверхности? Коэффициент отражения света ρ= 0,25.
РЕШЕНИЕ

19.29 Рентгеновские лучи с длиной волны λ0 = 70,8 пм испытывают комптоновское рассеяние на парафине. Найти длину волны рентгеновских лучей, рассеянных в направлениях: φ =π/2; φ =π
РЕШЕНИЕ

19.30 Какова была длина волны рентгеновского излучения, если при комптоновском рассеянии этого излучения графитом под углом φ = 60° длина волны рассеянного излучения оказалась равной λ = 25,4 пм
РЕШЕНИЕ

19.31 Рентгеновские лучи с длиной волны λ0 = 20 пм испытывают комптоновское рассеяние под углом φ = 90°. Найти изменение длины волны рентгеновских лучей при рассеянии, а также энергию и импульс электрона отдачи.
РЕШЕНИЕ

19.32 При комптоновском рассеянии энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи. Угол рассеяния φ =π/2 . Найти энергию и импульс рассеянного фотона.
РЕШЕНИЕ

19.33 Энергия рентгеновских лучей e = 0,6 МэВ. Найти энергию электрона отдачи, если длина волны рентгеновских лучей после комптоновского рассеяния изменилась на 20%.
РЕШЕНИЕ

19.34 Найти длину волны де Бройля для электронов, прошедших разность потенциалов U1 = 1 В и U2 = 100 B.
РЕШЕНИЕ

19.35 Решить предыдущую задачу для пучка протонов.
РЕШЕНИЕ

19.36 Найти длину волны де Бройля для электрона, движущегося со скоростью v = 10^6 м/с; атома водорода, движущегося со средней квадратичной скоростью при температуре T = 300 К; шарика массой m = 1 г, движущегося с v = 1 см/с
РЕШЕНИЕ

19.37 Найти длину волны де Бройля для электрона, имеющего кинетическую энергию W1 = 10 кэВ; W2 = 1 МэВ.
РЕШЕНИЕ

19.38 Заряженная частица, ускоренная разностью потенциалов U = 200 B. имеет длину волны де Бройля λ = 2,02 пм. Найти массу частицы, если ее заряд численно равен заряду электрона.
РЕШЕНИЕ

19.39 Составить таблицу значений длин волн де Бройля для электрона, движущегося со скоростью, равной: 2·10^8; 2,2·10^8; 2,4·10^8; 2,6·10^8; 2,8·10^8 м/с.
РЕШЕНИЕ

19.40 Альфа-частица движется пo окружности радиусом r = 8,3 мм в однородном магнитном поле, напряженность которого H = 18,9 кА/м. Найти длину волны де Бройля для a-частицы.
РЕШЕНИЕ

19.41 Найти длину волны де Бройля для атома водорода, движущегося при температуре T = 293 К с наиболее вероятной скоростью.
РЕШЕНИЕ

Условие задачи:

Найти массу фотона излучения с длиной волны 1 мкм.

Задача №11.1.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(lambda=1) мкм, (m-?)

Решение задачи:

Согласно формуле Планка, энергия фотона (E) пропорциональна частоте колебаний (nu) и определяется следующим образом:

[E = hnu;;;;(1)]

В этой формуле (h) – это постоянная Планка, равная 6,62·10^-34 Дж·с.

Известно, что частоту колебаний (nu) можно выразить через скорость света (c), которая равна 3·10⁸ м/с, и длину волны (lambda) по следующей формуле:

[nu = frac{c}{lambda };;;;(2)]

Подставим выражение (2) в формулу (1), тогда получим:

[E = frac{{hc}}{lambda };;;;(3)]

Так известен тот факт, что энергия фотона (E) связана с массой (m) по такой формуле:

[E = m{c^2};;;;(4)]

Приравняем (3) и (4), тогда:

[frac{{hc}}{lambda } = m{c^2}]

[frac{h}{lambda } = mc]

Из этого равенства выразим массу фотона (m):

[m = frac{h}{{lambda c}}]

Задача решена в общем виде, посчитаем численный ответ:

[m = frac{{6,62 cdot {{10}^{ – 34}}}}{{{{10}^{ – 6}} cdot 3 cdot {{10}^8}}} = 2,21 cdot {10^{ – 36}};кг]

Ответ: 2,21·10^-36 кг.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

11.1.13 Какой массой обладает фотон с длиной волны 0,6 мкм?
11.1.15 Определить импульс фотона, соответствующего рентгеновскому излучению с частотой
11.1.16 С какой скоростью должен двигаться электрон, чтобы его импульс был равен