Так как рычаг неоднородный, то он не будет в равновесии, если его подвесить за середину. Запишем условие равновесия рычага в первом случае:
m1gl1 + mgx = m2gl2. (1)
Так, как заведомо известно, что учебник имеет большую массу, чем груз в 100 г, то равновесие возможно, когда центр масс (тяжести) находится правее точки подвеса.
Во втором случае:
m1gl1/ + mgx = m2gl2/. (2)
Из (1) уравнения вычтем (2):
m1(l1 − l1/) = m2(l2 − 12/),
тогда искомая масса учебника:
m2 = (l1 − l1/) / (l2 − 12/) m1. (3)
После вычисления:
m2 = (50 − 42) / (17 − 15) ? 100 г = 400 г.
Определить массу рычага по данным таблицы нельзя. Так как в уравнении (1) или (2) две неизвестные: масса рычага и его плечо.
Момент силы. Условия равновесия рычага
- Устройство и виды рычагов
- Момент силы
- Правило моментов для двух сил
- Правило моментов для нескольких сил
- Применение рычагов в быту и технике
- Задачи
- Лабораторная работа №9. Проверка условия равновесия рычага
п.1. Устройство и виды рычагов
 |
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.
Рычаг состоит из перекладины и опоры. Назначение рычага – получить выигрыш в силе или расстоянии. |
В зависимости от взаимного расположения точки опоры и нагрузки различают три вида рычагов.
п.2. Момент силы
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.
Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.
На рисунке (l_1) – плечо силы (F_1, l_2) — плечо силы (F_2).
Силы вращают рычаг вокруг точки опоры – по часовой или против часовой стрелки.
Ось вращения проходит через точку опоры перпендикулярно плоскости вращения.
На рисунке сила (F_1) вращает рычаг против часовой стрелки, а сила (F_2) — по часовой стрелке.
Момент силы – это произведение силы, вращающей тело, на её плечо. $$ M=Fl $$ В системе СИ единица измерения момента силы — Н·м.
Момент силы определяется не для всего тела, а для некоторой его точки, удалённой от центра (оси) вращения. Эта величина имеет смысл только для вращающихся тел.
п.3. Правило моментов для двух сил
Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.
 |
$$ F_1l_1=F_2l_2 $$ |
п.4. Правило моментов для нескольких сил
Правило моментов для нескольких сил
Рычаг находится в равновесии, если сумма моментов всех сил, вращающих его по ходу часовой стрелки, равен сумме моментов всех сил, вращающих его против хода часовой стрелки.
Например:
 |
Силы (F_1, F_2, F_3) вращают рычаг против часовой стрелки, а сила (F_4) — по часовой стрелке. Поэтому: $$ F_1l_1+F_2l_2+F_3l_3=F_4l_4 $$ |
п.5. Применение рычагов в быту и технике
Рычаги первого рода
 Весы Предмет, вес которого нужно измерить, — это нагрузка, а гиря создает усилие. Они равны, так как находятся на одном расстоянии от точки опоры. |
 Рычажные весы Точка опоры смещена относительно центра. Грузило передвигается по основанию, пока не уравновесит взвешиваемый объект. |
 Гвоздодёр Усилие ручки увеличивается плечом и вытаскивает гвоздь. Нагрузкой здесь является сопротивление гвоздя. |
 Ручная тележка Небольшое усилие, прикладываемое к ручкам тележки, позволяет поднимать тяжелый груз. |
 Плоскогубцы Составной рычаг, пара простых рычагов, соединенных в точке опоры. Нагрузка — сопротивление предмета захвату инструментом. |
 Ножницы Составной рычаг первого рода, развивают мощное режущее действие очень близко к месту крепления. Нагрузка — сопротивление материала лезвиям. |
Рычаги второго рода
Рычаги третьего рода
п.6. Задачи
Задача 1. Для каждого положения тела укажите плечо силы.
При необходимости достраиваем линию действия силы и опускаем на неё перпендикуляр из точки опоры. Этот перпендикуляр и есть искомое плечо.
Задача 2. Грузы уравновешены на рычаге. Отношение плеч рычага 1:5. Масса большего груза 2,5 кг. Найдите массу меньшего груза.
Дано:
(frac{l_1}{l_2}=frac 15)
(m_1=2,5 text{кг})
__________________
(m_2-?)
По правилу моментов begin{gather*} F_1l_1=F_2l_2 end{gather*} На обоих концах рычага действуют силы тяжести: $$ F_1=m_1g, F_2=m_2g $$ Получаем: begin{gather*} m_1gl_1=m_2gl_2\[7pt] m_2=frac{m_1l_1}{l_2} end{gather*} Подставляем: $$ m_2=2,5cdot frac 15=0,5 (text{кг}) $$ Ответ: 0,5 кг
Задача 3. На концах рычага действуют силы 15 Н и 60 Н, направленные вниз. Рычаг находится в равновесии. Расстояние между точками приложения сил 1 м. Где расположена точка опоры?
Дано:
(F_1=15 text{Н})
(F_2=60 text{Н})
(l_1+l_2=1 text{м})
__________________
(l_1, l_2-?)
По правилу моментов begin{gather*} F_1l_1=F_2l_2. end{gather*} Получаем систему уравнений begin{gather*} left{ begin{array}{l l} 15l_1=60l_2 \ l_1+l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=4l_2 \ l_1+l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=4l_2 \ 4l_2+l_2=1 end{array} right. Rightarrow \[7pt] Rightarrow left{ begin{array}{l l} l_1=4l_2 \ 5l_2=1 end{array} right. Rightarrow left{ begin{array}{l l} l_1=0,8 \ l_2=0,2 end{array} right. end{gather*} Ответ: 0,8 м от точки приложения первой силы и 0,2 м от точки приложения второй силы.
Задача 4*. К балке, расположенной на двух опорах А и В подвешен груз массой 500 кг. Расстояние от точки подвеса груза к одному из концов балки в 4 раза больше, чем к другому. С какой силой балка давит на каждую из опор? Примите (gapprox 10 text{м/с}^2). Ответ запишите в килоньютонах.
Дано:
(m=500 text{кг})
(gapprox 10 text{м/с}^2)
(OB=4OA)
__________________
(F_A, F_B-?)
Сила тяжести (F_{text{т}}=mg), направленная вниз, уравновешивается силами реакции опор (F_A) и (F_B), направленными вверх. begin{gather*} F_A+F_B=mg end{gather*} По правилу моментов при равновесии begin{gather*} F_Acdot OA=F_Bcdot OB=F_Bcdot 4OARightarrow F_A=4F_B \[7pt] F_A+F_B=5F_B=mgRightarrow F_B=frac{mg}{5} end{gather*} Получаем: begin{gather*} F_B=frac{500cdot 10}{5}=1000 text{Н}=1 text{кН}, F_A=4cdot 100=4000 text{Н}=4 text{кН} end{gather*} Ответ: 4 кН и 1 кН
п.7. Лабораторная работа №9. Проверка условия равновесия рычага
Цель работы
Исследовать условия равновесия рычага под действием двух параллельных сил.
Теоретические сведения
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.
В работе используется рычаг 1-го рода, в котором опора располагается между точками приложения сил.
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг. Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.
Момент силы – это произведение силы, вращающей тело, на её плечо: (M=Fl).
Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.
 |
begin{gather*} M_1=M_2\[7pt] F_1l_1=F_2l_2 end{gather*} |
В работе используется лабораторный рычаг с отверстиями диаметром 4 мм, находящимися на расстоянии 5 см друг от друга. Отверстий нечетное количество; центральное отверстие (центр тяжести) используется для подвеса рычага на штативе в положении равновесия. Абсолютную погрешность определения плеча на данном рычаге принимаем равной половине диаметра отверстия $$ Delta l=frac D2=2 text{мм} $$
Для измерения веса груза используется динамометр с ценой деления $$ d=0,1 text{Н}. $$
Абсолютная погрешность определения веса $$ Delta_F=frac d2=0,05 text{Н}. $$
Относительные погрешности измерений: $$ delta_l=frac{Delta_l}{l}, delta_F=frac{Delta_F}{F}, delta_M=delta_l+delta_F $$
Абсолютная погрешность определения момента силы $$ Delta_M=Mcdot delta_M $$
Погрешности определения отношений сил и плечей: begin{gather*} r_F=frac{F_1}{F_2}, delta_{rF}=frac{Delta_F}{F_1}+frac{Delta_F}{F_2}, Delta_{rF}=frac{F_1}{F_2}cdot delta_{rF}\[7pt] r_l=frac{l_2}{l_1}, delta_{rF}=delta_{rl}frac{Delta_l}{l_1}+frac{Delta_l}{l_2}, Delta_{rl}=frac{l_2}{l_1}cdot delta_{rl} end{gather*}
Приборы и материалы
Лабораторный рычаг, штатив, стержень, динамометр, набор грузов.
Ход работы
1. Закрепите стержень в штативе, наденьте на него рычаг. Если стержень проходит через центральное отверстие рычага, он находится в равновесии.
2. Подвесьте три груза на динамометре, запишите их вес (F_1).
3. Подвесьте грузы слева от оси вращения рычага на расстоянии 5 см.
4. С помощью динамометра определите, какую силу нужно приложить на расстоянии 15 см справа от оси вращения, чтобы удерживать рычаг в равновесии.
5. Как направлены в этом случае силы, действующие на рычаг? Запишите длину плеч этих сил.
6. Найдите моменты сил (M_1) и (M_2), их относительные и абсолютные погрешности.
7. Вычислите отношение сил (frac{F_1}{F_2}) и плеч (frac{l_2}{l_1}) для этого случая, погрешности их определения.
8. Сделайте выводы.
Результаты измерений и вычислений
| (F_1, text{Н}) | (l_1, text{см}) | (F_2, text{Н}) | (l_2, text{см}) | (F_1/F_2) | (l_2/l_1) |
| 2,9 | 5 | 1,0 | 15 | 2,9 | 3,0 |
Погрешности прямых измерений: $$ Delta_l=2 text{мм}=0,2 text{см}, Delta_F=0,05 text{Н} $$ Найдем моменты сил и погрешности вычислений: begin{gather*} M_1=F_1cdot l_1=2,9cdot 5=14,5 (text{Н}cdot text{м})\[7pt] delta_{M1}=frac{Delta_l}{l_1}+frac{Delta_F}{F_1}=frac{0,2}{5}+frac{0,05}{2,9}approx 0,04+0,017=0,057=5,7text{%} \[7pt] Delta_{M1}=M_1cdot delta_{M1}=14,5cdot 0,057approx 0,8 (text{Н}cdot text{м})\[7pt] M_1=(14,5pm 0,8) text{Н}cdot text{м}\[7pt] \[7pt] M_2=F_2cdot l_2=1,0cdot 15=15,0 (text{Н}cdot text{м})\[7pt] delta_{M2}=frac{Delta_l}{l_2}+frac{Delta_F}{F_2}=frac{0,2}{15}+frac{0,05}{1,0}approx 0,013+0,05=0,063=6,3 text{%} \[7pt] Delta_{M2}=M_2cdot delta_{M2}=15,0cdot 0,063approx 0,9 (text{Н}cdot text{м})\[7pt] M_2=(15,0pm 0,9) text{Н}cdot text{м} end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ M_1=M_2 $$
Погрешность вычислений для (frac{F_1}{F_2}) begin{gather*} delta_{rF}=frac{Delta_F}{F_1}+frac{Delta_F}{F_2}=frac{0,05}{2,9}+frac{0,05}{1,0}approx 0,017+0,05=0,067=6,7text{%}\[7pt] Delta_{rF}=frac{F_1}{F_2}cdot delta_{rF}=2,9cdot 0,067approx 0,2\[7pt] frac{F_1}{F_2}=2,9pm 0,2 end{gather*}
Погрешность вычислений для (frac{l_2}{l_1}) begin{gather*} delta_{rl}=frac{Delta_l}{l_1}+frac{Delta_l}{l_2}=frac{0,2}{5}+frac{0,2}{15}approx 0,04+0,013=0,053=5,3text{%}\[7pt] Delta_{rl}=frac{l_2}{l_1}cdot delta_{rl}=3,0cdot 0,053approx 0,2\[7pt] frac{l_2}{l_1}=3,0pm 0,2 end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ frac{F_2}{F_2}=frac{l_2}{l_1} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Моменты сил, приложенных слева и справа от оси вращения рычага, равны $$ M_1=(14,5pm 0,8) text{Н}cdot text{м}, M_2=(15,0pm 0,9) text{Н}cdot text{м} $$ Таким образом, с учетом вычисленных погрешностей, (M_1=M_2) — правило моментов выполняется.
Отношения сил и плечей равны begin{gather*} frac{F_1}{F_2}=2,9pm 0,2, frac{l_2}{l_1}=3,0pm 0,2 end{gather*}
Таким образом, с учетом вычисленных погрешностей (frac{F_1}{F_2}=frac{l_2}{l_1}) — правило отношений выполняется.
Эксперименты подтвердили условие равновесия рычага.
Задачи на простые механизмы с решениями
Формулы, используемые на уроках «Задачи на простые механизмы,
условия равновесия рычага, блоки, золотое правило механики».
Название величины |
Обозначение |
Единица измерения |
Формула |
Сила |
F |
Н |
F1l1 = F2l2 |
Плечо силы |
l |
м |
|
Момент силы |
M |
Нм |
M = Fl |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
С помощью рычага рабочий поднимает плиту массой 120 кг. Какую силу он прикладывает к большему плечу рычага, равному 2,4 м, если меньшее плечо 0,8 м?
Задача № 2.
На концах рычага действуют силы 20 Н и 120 Н. Расстояние от точки опоры до большей силы равно 2 см. Определите длину рычага, если рычаг находится в равновесии.
Задача № 3.
На рисунке изображен рычаг, имеющий ось вращения в точке О. Груз какой массы надо подвесить в точке В для того, чтобы рычаг был в равновесии?
Задача № 4.
На меньшее плечо рычага действует сила 300 Н, на большее — 20 Н. Длина меньшего плеча 5 см. Определите длину большего плеча.
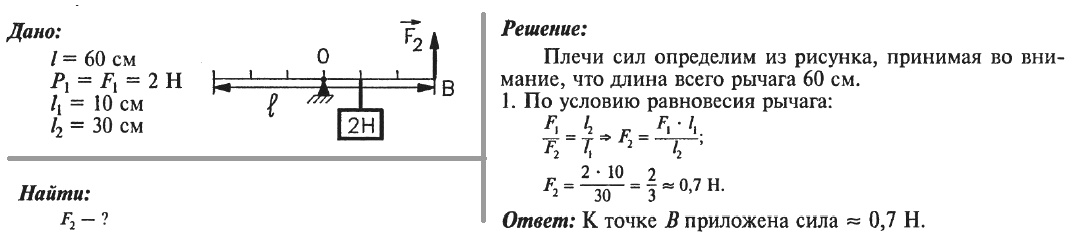
Задача № 5.
Рычаг длиной 60 см находится в равновесии. Какая сила приложена в точке В?
Задача № 6.
Момент силы действующей на рычаг, равен 20 Н*м. Найти плечо силы 5 Н, если рычаг находится в равновесии.
Задача № 7.
Какое усилие необходимо приложить, чтобы поднять груз 1000 Н с помощью подвижного блока? Какая совершится работа при подъеме груза на 1 м? (Вес блока и трение не учитывать).
Задача № 8.
Система блоков находится в равновесии. Определите вес правого груза. (Вес блоков и силу трения не учитывать).
Задача № 9.
При помощи подвижного блока поднимают груз, прилагая силу 105 Н. Определите силу трения, если вес блока равен 20 Н, а вес груза 180 Н.
Задача № 10.
ОГЭ
Стержень цилиндрической формы длиной l = 40 см состоит на половину своей длины из свинца и наполовину — из железа. Найти расстояние от центра тяжести до центра симметрии стержня. Плотность свинца p1 = 11,4 г/см3, плотность железа p2 = 7,8 г/см3.
Решение. Центр тяжести тела (центр масс) — точка приложения силы притяжения его к земле — веса тела P. У тел, имеющих какую-либо симметрию, он совпадает с центром симметрии. Например, у однородного цилиндра центр тяжести расположен на его оси в центре цилиндра. Тело, закреплённое на оси, проходящей через его центр тяжести, находится в состоянии безразличного равновесия. Мысленно закрепим стержень AB на оси, перпендикулярной стержню и проходящей через его центр тяжести C, отстоящий от его геометрического центра O на расстояние x в сторону более тяжёлой половины стержня. Центры инерций половинок размещены на расстояниях l/4 от середины стержня.
х = (11,4–7,8)/(11,4+7,8) • 0,4/4 = 0,01875 ≈ 0,019 (м)
Ответ: 1,9 см.
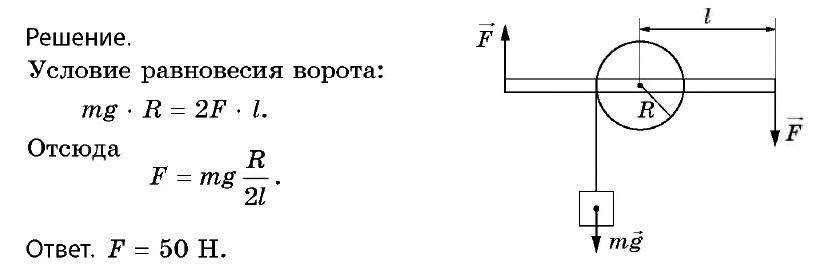
Задача № 11.
ЕГЭ
Масса якоря корабля m = 50 кг. Радиус барабана, на который наматывают якорную цепь, R = 0,2 м, длина каждой из двух ручек ворота l = 1 м. Какую силу нужно приложить к каждой из них, чтобы поднять якорь?
Краткая теория для решения задачи на простые механизмы.
Конспект урока «Задачи на простые механизмы с решениями».
Следующая тема: «Задачи на КПД простых механизмов».
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,985 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Очень надо!
И можно, пожалуйста, с объяснением
К рычагу подвесили груз и прикрепили нить так, как показано на рисунке. (см. рисунок) Сила натяжения нити равна 6 Н. Найдите массу груза. Ответ дайте в кг