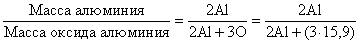Как найти массу одного атома физика - Исправление недочетов и поиск решений вместе с Examum.ru

Download Article

Atomic mass is the sum of all the protons, neutrons, and electrons in a single atom or molecule. However, the mass of an electron is so small, it is considered negligible and not included in the calculation.^[1] Though technically incorrect, the term is also often used to refer to the average atomic mass of all of the isotopes of one element. This second definition is actually the relative atomic mass, also known as the atomic weight, of an element.^[2] The atomic weight takes into account the average of the masses of naturally occurring isotopes of the same element. Chemists need to distinguish between these two types of atomic mass to guide their work — an incorrect value for atomic mass can, for instance, lead to an incorrect calculation of an experiment’s yield.

1
Understand how atomic mass is represented. Atomic mass, the mass of a given atom or molecule, can be expressed in standard SI mass units — grams, kilograms, etc. However, because atomic masses, when expressed in these terms, are incredibly small, atomic mass is often expressed in unified atomic mass units (usually shortened to «u» or «amu») or in Dalton’s (Da). The standard for one atomic mass unit is equal to 1/12th of the mass of a standard carbon-12 isotope.^[3]
- The atomic mass is the number of grams of the element in one mole of atoms of the element. This is a very useful property when it comes to practical calculations, as it allows easy conversion between the mass and moles of a given quantity of atoms or molecules of the same type.
2
Locate atomic mass on the periodic table. Most standard periodic tables list the relative atomic masses (atomic weights) of each element. This is almost always written as a number at the bottom of the element’s square on the table, under its one or two letter chemical symbol. This number is usually expressed as a decimal rather than as a whole number.
- Note that the relative atomic masses listed on the periodic table are average values for the associated element. Chemical elements have different isotopes — chemical forms that differ in mass because of the addition or subtraction of one or more neutrons to the atom’s nucleus.^[4] Thus, the relative atomic mass listed on the periodic table is suitable as an average value for atoms of a certain element, but not as the mass of a single atom of that element.
- Relative atomic masses, as listed on the periodic table, are used to calculate molar masses for atoms and molecules. Atomic masses, when expressed in amu, as on the periodic table, are technically unitless. However, by simply multiplying an atomic mass by 1 g/mol, a workable quantity is obtained for an element’s molar mass — the mass (in grams) of one mole of an element’s atoms.
- For example, the atomic mass of iron is 55.847 amu, which means one mole of iron atoms would weigh 55.847 grams.
Advertisement
3
Understand that periodic table values are an average atomic mass for an element. As has been noted, the relative atomic masses listed for each element on the periodic table are average values of all of an atom’s isotopes. This average value is valuable for many practical calculations — like, for instance, calculating the molar mass of a molecule comprised of several atoms. However, when dealing with individual atoms, this number is sometimes insufficient.
- Because it’s an average of several different types of isotopes, the value on the periodic table isn’t the exact value for any single atom’s atomic mass.
- The atomic masses for individual atoms must be calculated by taking into account the exact number of protons and neutrons in a single atom.

1
Find the atomic number of the element or isotope. The atomic number is the number of protons in an element, and never varies.^[5] For example, all hydrogen atoms, and only hydrogen atoms, have 1 proton. Sodium has an atomic number of 11 because its nucleus has 11 protons, while oxygen has an atomic number of 8 because its nucleus has 8 protons. You can find the atomic number of any element on the periodic table — in nearly all standard periodic tables: it’s the number above an element’s 1 or 2-letter chemical symbol. This number will always be a positive whole number.
- Let’s say that we’re working with the carbon atom. Carbon always has 6 protons, so we know its atomic number is 6. We can also see on the periodic table that the square for carbon (C) has a «6» at the top, signifying that carbon’s atomic number is 6.
- Note that an element’s atomic number doesn’t have any direct bearing on its relative atomic mass as listed on the periodic table. Though, especially among elements at the top of the periodic table, it may seem that an atoms’ atomic mass is about twice its atomic number, atomic mass isn’t ever calculated by doubling an element’s atomic number.
2
Find the number of neutrons in the nucleus. The number of neutrons can vary among atoms of a certain element. While 2 atoms with the same number of protons and differing numbers of neutrons are both the same element, they are different isotopes of that element. Unlike the number of protons in an element, which never changes, the number of neutrons in atoms of a certain element can vary often enough that the average atomic mass of the element must be expressed as a decimal value between two whole numbers.
- The number of neutrons can be determined by the isotope designation of the element. For example, carbon-14 is a naturally occurring radioactive isotope of carbon-12. You will often see an isotope designated with the number as a superscript before the element symbol: ¹⁴C. The number of neutrons is calculated by subtracting the number of protons from the isotope number: 14 – 6 = 8 neutrons.
- Let’s say the carbon atom we’re working with has six neutrons (¹²C). This is by far the most common isotope of carbon, accounting for nearly 99% of all carbon atoms.^[6] However, about 1% of carbon atoms have 7 neutrons (¹³C). Other types of carbon atoms with more or less than 6 or 7 neutrons exist in very small amounts.
3
Add the proton and neutron count. This is the atomic mass of that atom. Don’t worry about the number of electrons orbiting the nucleus — their combined mass is very, very small, so, in most practical cases, it won’t significantly affect your answer.^[7]
- Our carbon atom has 6 protons + 6 neutrons = 12. The atomic mass of this specific carbon atom is 12. If it was a carbon-13 isotope, on the other hand, we would know that it has 6 protons + 7 neutrons = an atomic weight of 13.
- The actual atomic weight of carbon-13 is 13.003355^[8], and is more precise because it was determined experimentally.
- Atomic mass is very close to the isotope number of an element. For basic calculation purposes, isotope number is equal to atomic mass. When determined experimentally, the atomic mass is slightly higher than the isotope number due to the very small mass contribution from electrons.

1
Determine which isotopes are in the sample. Chemists often determine the relative proportions of isotopes in a given sample by using a special tool called a mass spectrometer. However, at student-level chemistry, this information is often provided for you on school tests, etc., in the form of established values from scientific literature.
- For our purposes, let’s say we’re working with the isotopes carbon-12 and carbon-13.
2
Determine the relative abundance of each isotope in the sample. Within a given element, different isotopes appear in different proportions. These proportions are almost always expressed as percentages. Some isotopes will be very common, while others will be very rare — at times, so rare that they can barely be detected. This information can be determined through mass spectrometry or from a reference book.
- Let’s say that the abundance of carbon-12 is 99% and the abundance of carbon-13 is 1%. Other carbon isotopes do exist, but they exist in quantities so small that, for this example problem, they can be ignored.
3
Multiply the atomic mass of each isotope by its proportion in the sample. Multiply the atomic mass of each isotope by its percent abundance (written as a decimal). To convert a percentage to a decimal, simply divide it by 100. The converted percentages should always add up to 1.
- Our sample contains carbon-12 and carbon-13. If carbon-12 makes up 99% of the sample and carbon-13 makes up 1% of the sample, multiply 12 (the atomic mass of carbon-12) by 0.99 and 13 (the atomic mass of carbon-13) by 0.01.
- A reference book will give percent proportions based on all the known amounts of an element’s isotopes. Most chemistry textbooks include this information in a table at the end of the book. A mass spectrometer can also yield the proportions for the sample being tested.
4
Add the results. Sum the products of the multiplications you performed in the previous step. The result of this addition is the relative atomic mass of your element — the average value of the atomic masses of your element’s isotopes. When discussing an element in general, and not specific isotopes of that element, this value is used.
- In our example, 12 x 0.99 = 11.88 for carbon-12, while 13 x 0.01 = 0.13 for carbon-13. The relative atomic mass of our example is 11.88 + 0.13 = 12.01.

Add New Question

Question

How do I find the mass number of an atom?

Add the protons and neutrons together to find the mass, or add the masses of the isotopes multiplied by the atom’s natural abundance.
Question

If 1 amu is 1/12 of a carbon 12 atom, why is it that when I add the masses of the individual parts of a carbon 12 atom, I get more than 12 amu?

1 u = 1/12 the mass of carbon 12 by definition. You’re adding the masses of uncombined protons and neutrons, 1.0073 u and 1.0087 u respectively. But when those particles fuse together to form an atom, some of the mass is converted into energy according to E=mc^2. The lost mass is called the «mass defect», and the equivalent amount of energy is the «binding energy.»
Question

How can I find the mass of any atom to convert it in a.m.u.?

We can find the mass of any atom by adding the electrons, protons and neutrons.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Things You’ll Need

Chemistry reference book
Calculator

References

About This Article

Article SummaryX

To calculate atomic mass, start by finding the atomic number of the element, which is the number above the element on the periodic table. Next, find the number of neutrons in the nucleus by subtracting the atomic number from the isotope number. Finally, add the atomic number and the number of neutrons to get the atomic mass. To learn how to locate an element’s atomic mass on the periodic table, keep reading!

Did this summary help you?

Thanks to all authors for creating a page that has been read 954,091 times.

Reader Success Stories

«I couldn’t do my homework for my science teacher without this article, it has helped me understand the topic…» more

Did this article help you?

Источник

Загрузить PDF

Атомной массой называется сумма масс всех протонов, нейтронов и электронов, из которых состоит тот или иной атом или молекула.^[1] По сравнению с протонами и нейтронами масса электронов очень мала, поэтому она не учитывается в расчетах.^[2] Хотя это и некорректно с формальной точки зрения, нередко данный термин используется для обозначения средней атомной массы всех изотопов элемента. На самом деле это относительная атомная масса, называемая также атомным весом элемента.^[3] Атомный вес – это среднее значение атомных масс всех изотопов элемента, встречающихся в природе. Химики должны различать эти два типа атомной массы при выполнении своей работы – неправильное значение атомной массы может, к примеру, привести к неправильному результату для выхода продукта реакции.

1
Изучите как записывается атомная масса. Атомная масса, то есть масса данного атома или молекулы, может быть выражена в стандартных единицах системы СИ – граммах, килограммах и так далее. Однако в связи с тем, что атомные массы, выраженные в этих единицах, чрезвычайно малы, их часто записывают в унифицированных атомных единицах массы, или сокращенно а.е.м. – атомные единицы массы. Одна атомная единица массы равна 1/12 массы стандартного изотопа углерод-12.^[4]
- Атомная единица массы характеризует массу одного моля данного элемента в граммах. Эта величина очень полезна при практических расчетах, поскольку с ее помощью можно легко перевести массу заданного количества атомов или молекул данного вещества в моли, и наоборот.
2
Найдите атомную массу в периодической таблице Менделеева. В большинстве стандартных таблиц Менделеева содержатся атомные массы (атомные веса) каждого элемента. Как правило, они приведены в виде числа в нижней части ячейки с элементом, под буквами, обозначающими химический элемент. Обычно это не целое число, а десятичная дробь.
- Обратите внимание, что все относительные атомные массы, указанные в таблице Менделеева, для каждого элемента являются средними значениями. У химических элементов есть различные изотопы – химические разновидности, имеющие разные массы из-за дополнительных или отсутствующих нейтронов в атомном ядре.^[5] Следовательно, относительные атомные массы, перечисленные в периодической таблице, могут использоваться как среднее значение для атомов определенного элемента, но не как масса одного атома данного элемента.
- Относительные атомные массы, приведенные в периодической таблице, используются для расчета молярных масс атомов и молекул. Атомные массы, выраженные в а.е.м. (как в таблице Менделеева), по существу безразмерны. Однако просто умножив атомную массу на 1 г/моль, мы получаем полезную характеристику элемента – массу (в граммах) одного моля атомов этого элемента.
3
Помните о том, что в периодической таблице приведены средние атомные массы элементов. Как было отмечено ранее, относительные атомные массы, указанные для каждого элемента в периодической системе, являются средними значениями масс всех изотопов атома. Это среднее значение ценно для многих практических целей: к примеру, оно используется при расчете молярной массы молекул, состоящих из нескольких атомов. Однако когда вы имеете дело с отдельными атомами, этого значения, как правило, бывает недостаточно.
- Поскольку средняя атомная масса представляет собой усредненное значение для нескольких изотопов, величина, указанная в таблице Менделеева не является точным значением атомной массы любого единичного атома.
- Атомные массы отдельных атомов необходимо рассчитывать с учетом точного числа протонов и нейтронов в единичном атоме.
Реклама

1
Найдите атомный номер данного элемента или его изотопа. Атомный номер – это количество протонов в атомах элемента, оно никогда не изменяется.^[6] Например, все атомы водорода, причем только они, имеют один протон. Атомный номер натрия равен 11, поскольку в его ядре одиннадцать протонов, тогда как атомный номер кислорода составляет восемь, так как в его ядре восемь протонов. Вы можете найти атомный номер любого элемента в периодической таблице Менделеева – практически во всех ее стандартных вариантах этот номер указан над буквенным обозначением химического элемента. Атомный номер всегда является положительным целым числом.
- Предположим, нас интересует атом углерода. В атомах углерода всегда шесть протонов, поэтому мы знаем, что его атомный номер равен 6. Кроме того, мы видим, что в периодической системе, в верхней части ячейки с углеродом (C) находится цифра «6», указывающая на то, что атомный номер углерода равен шести.
- Обратите внимание, что атомный номер элемента не связан однозначно с его относительной атомной массой в периодической системе. Хотя, особенно для элементов в верхней части таблицы, может показаться, что атомная масса элемента вдвое больше его атомного номера, она никогда не рассчитывается умножением атомного номера на два.
2
Найдите число нейтронов в ядре. Количество нейтронов может быть различным для разных атомов одного и того же элемента. Когда два атома одного элемента с одинаковым количеством протонов имеют разное количество нейтронов, они являются разными изотопами этого элемента. В отличие от количества протонов, которое никогда не меняется, число нейтронов в атомах определенного элемента может зачастую меняться, поэтому средняя атомная масса элемента записывается в виде десятичной дроби со значением, лежащим между двумя соседними целыми числами.
- Количество нейтронов можно определить по обозначению изотопа элемента. Например, углерод-14 представляет собой радиоактивный изотоп углерода-12, встречающийся в природе. Часто номер изотопа указывается в виде надстрочного числа, стоящего перед символом элемента: ¹⁴C. Количество нейтронов находится путем вычитания числа протонов из номера изотопа: 14 – 6 = 8 нейтронов.
- Допустим, что интересующий нас атом углерода имеет шесть нейтронов (¹²C). Это наиболее распространенный изотоп углерода, насчитывающий около 99% всех атомов данного элемента.^[7] Однако около 1% атомов углерода имеют 7 нейтронов (¹³C). Другие виды атомов углерода имеют больше 7 или меньше 6 нейтронов и существуют в очень малых количествах.
3
Сложите количество протонов и нейтронов. Это и будет атомной массой данного атома. Не обращайте внимания на количество электронов, которые окружают ядро – их суммарная масса чрезвычайно мала, поэтому они практически не влияют на ваши расчеты.
- Наш атом углерода имеет 6 протонов + 6 нейтронов = 12. Таким образом, атомная масса данного атома углерода равна 12. Если бы это был изотоп «углерод-13», то мы бы знали, что у него есть 6 протонов + 7 нейтронов = атомная масса 13.
- В действительности атомная масса углерода-13 составляет 13,003355^[8], причем это значение является более точным, поскольку было определено экспериментальным путем.
- Атомная масса очень близка к номеру изотопа. Для удобства вычислений номер изотопа часто полагают равным атомной массе. Экспериментально определенные значения атомной массы немного превышают номер изотопа из-за очень малого вклада со стороны электронов.
Реклама

1
Определите, какие изотопы содержатся в образце. Химики часто определяют соотношение изотопов в конкретном образце с помощью специального прибора под названием масс-спектрометр. Однако при обучении эти данные будут предоставлены вам в условиях заданий, контрольных и так далее в виде значений, взятых из научной литературы.
- В нашем случае допустим, что мы имеем дело с двумя изотопами: углеродом-12 и углеродом-13.
2
Определите относительное содержание каждого изотопа в образце. Для каждого элемента различные изотопы встречаются в разных соотношениях. Эти соотношения почти всегда выражают в процентах. Некоторые изотопы встречаются очень часто, тогда как другие очень редки – временами настолько, что их с трудом можно обнаружить. Эти величины можно определить с помощью масс-спектрометрии или найти в справочнике.
- Допустим, что концентрация углерода-12 равна 99%, а углерода-13 – 1%. Другие изотопы углерода действительно существуют, но в количествах настолько малых, что в данном случае ими можно пренебречь.
3
Умножьте атомную массу каждого изотопа на его концентрацию в образце. Умножьте атомную массу каждого изотопа на его процентное содержание (выраженное в виде десятичной дроби). Чтобы перевести проценты в десятичную дробь, просто разделите их на 100. Полученные концентрации в сумме всегда должны давать 1.
- Наш образец содержит углерод-12 и углерод-13. Если углерод-12 составляет 99% образца, а углерод-13 – 1%, то необходимо умножить 12 (атомная масса углерода-12) на 0,99 и 13 (атомная масса углерода-13) на 0,01.
- В справочниках даются процентные соотношения, основанные на известных количествах всех изотопов того или иного элемента. Большинство учебников по химии содержат эту информацию в виде таблицы в конце книги. Для изучаемого образца относительные концентрации изотопов можно также определить с помощью масс-спектрометра.
4
Сложите полученные результаты. Просуммируйте результаты умножения, которые вы получили в предыдущем шаге. В результате этой операции вы найдете относительную атомную массу вашего элемента – среднее значение атомных масс изотопов рассматриваемого элемента. Когда рассматривается элемент в целом, а не конкретный изотоп данного элемента, используется именно эта величина.
- В нашем примере 12 x 0,99 = 11,88 для углерода-12, и 13 x 0,01 = 0,13 для углерода-13. Относительная атомная масса в нашем случае составляет 11,88 + 0,13 = 12,01.
Реклама

Советы

Некоторые изотопы менее стабильны, чем другие: они распадаются на атомы элементов с меньшим количеством протонов и нейтронов в ядре с выделением частиц, входящих в состав атомного ядра. Такие изотопы называют радиоактивными.

Что вам понадобится

Справочник по химии
Калькулятор

Об этой статье

Эту страницу просматривали 136 679 раз.

Была ли эта статья полезной?

Источник

Как определить массу атома

Для того чтобы определить массу атома, найдите молярную массу одноатомного вещества, используя таблицу Менделеева. Затем эту массу поделите на число Авогадро (6,022•10^(23)). Это и будет масса атома, в тех единицах, в которых измерялась молярная масса. Масса атома газа находится через его объем, который легко измерить.

Вам понадобится

Для определения массы атома вещества возьмите таблицу Менделеева, рулетку или линейку, манометр, термометр.

Инструкция

Определение массы атома твердого тела или жидкости Для определения массы атома вещества, определите его природу (из каких атомов оно состоит). В таблице Менделеева найдите ячейку, в которой описывается соответствующий элемент. Найдите массу одного моля этого вещества в граммах на моль, которая находится в этой ячейке (это число соответствует массе атома в атомных единицах массы). Поделите молярную массу вещества на 6,022•10^(23) (число Авогадро), результатом будет масса атома данного вещества в граммах. Можно определить массу атома и другим способом. Для этого атомную массу вещества в атомных единицах массы взятую в таблице Менделеева умножьте на число 1,66•10^(-24). Получите массу одного атома в граммах.

Определение массы атома газа В том случае, если в сосуде есть газ неизвестной природы, определите его массу в граммах, взвесив пустой сосуд и сосуд с газом, и найдите разность их масс. После этого измерьте объем сосуда с помощью линейки или рулетки, с последующим произведением расчетов или другими методами. Результат выразите в кубических метрах. Манометром измерьте давление газа внутри сосуда в паскалях, и измерьте его температуру термометром. Если шкала термометра проградуирована в градусах Цельсия, определите значение температуры в Кельвинах. Для этого к значению температуры на шкале термометра прибавьте число 273.

Для определения массы молекулы газа массу данного объема газа умножьте на его температуру и число 8,31. Результат поделите на произведение давления газа, его объема и числа Авогадро 6,022•10^(23) (m0=m•8,31•T/(P•V•NА)). Результатом будет масса молекулы газа в граммах. В том случае, если известно, что молекула газа двухатомная (газ не инертный) получившееся число поделите на 2. Помножив результат на 1,66•10^(-24) можно получить его атомную массу в атомных единицах массы, и определить химическую формулу газа.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Бронштейн М.П. Как был взвешен атом //Квант. — 1970. — № 2. — С. 26-35.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Предисловие

К концу прошлого века в физике и химии утвердилась, как тогда говорили, гипотеза об атомах и молекулах — мельчайших частицах, из которых составлены все тела окружающего нас мира. В химии атомная гипотеза позволила понять и очень удобно описывать химические реакции: всякая реакция — это просто соединение атомов в молекулы или, наоборот, разложение молекул на атомы или группы атомов. Из анализа состава различных молекул химики сумели выяснить, что атомы разных элементов обладают различными массами. Им даже удалось узнать, во сколько раз один атом тяжелее или легче другого; уже к началу второй половины XIX столетия были известны так называемые атомные веса всех открытых к тому времени химических элементов, то есть числа, показывающие, во сколько раз атом данного химического элемента тяжелее самого легкого из атомов — водорода. Знаменитый русский химик Д. И. Менделеев, расположив химические элементы в порядке возрастания атомных весов, показал в 1869 году, что они образуют определенную систему, в которой свойства элементов периодически повторяются (периодическая система). В физике гипотеза об атомах и молекулах играла не менее важную роль. Она позволила физикам составить себе ясное представление о множестве самых различных явлений. Она помогла понять, что такое тепло и холод, почему тела при нагревании расширяются, почему всякое вещество может быть твердым, жидким и газообразным и многое другое. Чтобы все это понять, нужно было только дополнительно предположить, что атомы и молекулы непрерывно и беспорядочно движутся и что между ними действуют силы притяжения и отталкивания. Но при всем этом атомы оставались только некоторым представлением в головах людей. Их не только никто не видел, потому что они очень малы, но никто не знал, насколько они малы, каковы массы атомов, сколько атомов в том или ином теле. Нельзя сказать, чтобы не делались попытки все это как-то узнать. Но эти попытки не приводили к убедительным результатам. У некоторых ученых появилась даже уверенность в том, что об атомах и молекулах ничего и нельзя будет узнать, потому что их на самом деле не существует. Эти ученые полагали, что атомы — это нечто вроде меридианов и параллелей на географической карте: ими удобно пользоваться, но реально в природе их нет. Физики, однако, не теряли надежду доказать реальность атомов и молекул, взвесить их, сосчитать их число, определить их размеры.

В предлагаемом отрывке из книги выдающегося советского физика-теоретика Матвея Петровича Бронштейна «Атомы, электроны, ядра» рассказывается о том, как впервые удалось измерить массу атомов и даже сосчитать их. Эта книга, изданная в 1935 году небольшим тиражом (всего 10 000 экземпляров), давно уже стала библиографической редкостью.

Публикацию подготовил профессор А.К. Кикоин. Сделанные им добавления взяты в прямые скобки.

Как был взвешен атом

… И в конце концов атом действительно удалось взвесить. Этому помогло одно очень странное явление, открытое еще в первой половине XIX века и на которое физики в свое время не обратили должного внимания. Это явление называется брауновским движением.

В 1828 году знаменитый английский ботаник Роберт Браун проделал одно в высшей степени интересное наблюдение. Испытывая только что присланный ему новый усовершенствованный микроскоп с ахроматическим объективом, Роберт Браун вздумал рассмотреть с помощью этого микроскопа ничтожную каплю жидкости, содержащуюся в крохотных зернышках пыльцы растений. В такой жидкости всегда имеется большее количество микроскопических твердых частиц. Как удивлен был Браун, когда увидел, что эти частицы не остаются на месте, а движутся, движутся непрерывно, точно исполняя какой-то фантастический танец! Когда в поле зрения микроскопа было видно много таких частиц, то получалось такое же впечатление, как от тучи каких-то мельчайших мошек. Твердые частицы микроскопических размеров, находящиеся в жидкости, движутся, как если бы они были живыми… Но уже Роберт Браун, который первым наблюдал это хаотическое движение микроскопических частиц, получившее свое название от его имени, пришел к другому заключению: частицы движутся не потому, что они живые… Так утверждал Браун, и это было подтверждено многочисленными последующими наблюдениями.

Можно было бы думать, что брауновское движение микроскопических частиц вызывается какими-то потоками в самой жидкости, связанными с разностью давлений в различных точках жидкости. Всякому приходилось наблюдать движение пылинок в воздухе, освещенном падающими сбоку солнечными лучами. Это движение действительно связано с такими токами воздуха, но брауновское движение имеет совершенно другой характер. В самом деле, если внимательно наблюдать за движением пылинок в солнечном луче, то легко заметить, что соседние пылинки, попавшие в одну и ту же небольшую струю воздуха, движутся в одну и ту же сторону. А если наблюдать за брауновским движением микроскопических частиц, то оказывается, что между направлением движения соседних частиц нет решительно ничего общего: частицы движутся совершенно независимо друг от друга, даже если им случается подойти друг к другу на самое крохотное расстояние, равное диаметру отдельной частички. Значит, совсем не от токов жидкости происходит это непостижимое и фантастическое движение микроскопических твердых частичек.

Во второй половине XIX века брауновское движение подробно исследовал французский физик Гуи. Он проделал целый ряд опытов, которые убедили его в том, что причина брауновского движения скрыта в самой жидкости. Не от внутренних токов жидкости, вызванных ничтожными разностями температур, и не от внешних толчков и сотрясений происходит брауновское движение. Гуи пробовал сравнивать брауновское движение в лаборатории, расположенной на шумной улице, цо которой проезжают тяжелые экипажи, с тем же брауновским движением, наблюдаемым ночью в глухом подвале в деревне. Разницы не получалось никакой. Толчки от экипажей заметны, но они сказываются не на хаотическом движении брауновских частиц, а на движении всей капельки, жидкости в целом: двигаясь, как целое, капелька увлекает за собой все частицы в одном и том же направлении, и это движение очень легко отличить от накладывающегося на него хаотического движения брауновских частиц, происходящего по всем возможным направлениям.

Гуи убедительно доказал, что брауновское движение, как уже предполагал и сам Браун, нисколько не связано с тем, что жидкость, в которой оно наблюдается, взята из живого существа — из растения: искусственно приготовленные жидкости с взвешенными в них микроскопическими частицами, в которых нет ничего живого, тоже обнаруживают брауновское движение. В 1881 году польский физик Бодашевский показал, что брауновское движение происходит и в газах, а не только в жидкостях.

Для того чтобы наблюдать брауновское движение, он рассматривал при боковом освещении микроскопические частички, образующие табачный дым. Крохотные частички угля, из которых состоит дым, плясали во все стороны совершенно таким же образом, как плясали твердые частички, наблюдавшиеся Робертом Брауном в жидкости.

Настоящую причину брауновского движения угадал в 70-х годах прошлого столетия бельгиец Карбонель. Его объяснение, гениальное по своей простоте, состоит в следующем: микроскопические частицы движутся потому, что они испытывают толчки со стороны невидимых молекул и атомов окружающей их жидкости. Рассматривая движение брауновских частичек, мы получаем некоторое представление о том, как движутся невидимые молекулы жидкости, совершенно таким же образом, как мы угадываем о волнении на море, когда, стоя далеко от берега, видим качание лодки, швыряемой волнами во все стороны. Брауновское движение является поэтому мостом, соединяющим невидимый мир атомов и молекул с миром, доступным восприятию при помощи наших органов чувств.

Почему брауновское движение можно наблюдать только в том случае, когда частички очень малы? Очень просто, отвечает на этот вопрос Карбонель; если поверхность частицы велика, то количество толчков, получаемых ею справа, всегда окажется приблизительно равным количеству толчков, получаемых ею же слева, и ничтожное различие в количестве толчков будет совершенно недостаточно для того, чтобы сдвинуть с места большую и тяжелую частицу. Если же частица имеет ничтожную массу и ничтожные размеры, то в хаосе молекулярных движений жидкости всегда может случиться, что с одной стороны частицы будет в данный момент случайно больше толчков, чем с другой, а поэтому легкоподвижная частица двинется в ту сторону, куда ее толкнут молекулы. Через какой-то очень короткий промежуток времени избыток молекулярных толчков будет сдвигать брауновскую частицу уже по другому направлению, еще через какой-то короткий промежуток времени — по третьему и т. д.

Если это предложенное Карбонелем объяснение правильно, то чем частицы легче и мельче, тем брауновское движение должно быть интенсивнее. Так и есть в действительности — уже Браун сумел это заметить. Кроме того, ведь мы знаем, что движение молекул жидкости происходит тем быстрее, чем выше температура; и в самом деле, Гуи нашел, что при повышении температуры брауновское движение делается все интенсивнее и интенсивнее. Когда Жигмонди изобрел ультрамикроскоп и смог наблюдать ничтожнейшие частицы золота в коллоидном растворе (диаметр частиц меньше миллионной доли сантиметра), то брауновское движение этих частиц оказалось таким быстрым, что получилось какое-то сплошное мелькание. Жигмонди описывает свое первое впечатление так: «Это какое-то непрерывное прыганье, пляска, скакание, столкновения и разлетания, так что трудно разобраться в этой путанице»…

Распределение зернышек по высоте в гуммигутовой эмульсии

Мы переходим теперь к рассказу о классических работах, которые сделал французский физик Жан Перрен (1908 г.). В этих работах было окончательно проверено и установлено,что брауновское движение в жидкостях вызвано движением молекул и тем самым дано решающее доказательство действительного существования молекул и атомов.

Перрен брал кусочки резиновой смолы «гуммигута» и растирал их рукой в воде, пока она не становилась ярко-желтого цвета. После этого Перрен брал немножко такой жидкости под микроскоп. Под микроскопом оказывалась, что гуммигут на самом деле не растворился в воде, а распался на множество шаровидных мелких зернышек, которые разбрелись по всему объему воды. Зернышки эти очень различны по размерам. А Перрену хотелось иметь такую жидкость, в которой были бы совершенно одинаковые по размерам частицы гуммигута. Для этого он воспользовался «центрифугой» (центробежной машиной), такой же самой, какой пользуются на крупных молочных фермах для отделения сливок от молока или же в медицинских лабораториях для удаления кровяных шариков из крови, после чего остается однородная жидкость — кровяная плазма. Центрифуга Перрена делала 2500 оборотов в минуту, и возникающая при этом центробежная сила выбрасывала из жидкости зернышки гуммигута. Перпендикулярно к оси центрифуги были расположены стеклянные пробирки, в которых содержалась эмульсия гуммигута (так называется вода с взвешенными в ней частичками гуммигута).

Первыми выпадали тяжелые частицы, а вслед за ними и легкие. Это давало возможность отделить частицы друг от друга по весу (а значит, и по размерам, потому что все частицы сделаны из одного и того же материала, и поэтому, чем больше их масса, тем больше и размеры).

Это очень кропотливая и тяжелая работа: приходится работать целый месяц для того, чтобы из одного килограмма гуммигута получить несколько десятых или даже сотых долей грамма круглых зерен нужной величины. Таким образом, Перрен сумел получить несколько порций эмульсии с диаметром зерен в 0,5, 0,46, 0,37, 0,21 и 0,14 микрона (микрон — это тысячная доля миллиметра).

С помощью таких эмульсий Жан Перрен произвел множество замечательных опытов, о которых мы здесь и расскажем. Он поместил каплю эмульсии с определенным диаметром зерен в плоскую ванночку (кюветку) с глубиной 0,1 мм. Кюветка была затем покрыта тонким покровным стеклышком, края которого были залиты парафином: таким образом, капля оказалась размазанной в сосуде, в котором она герметически заперта, так что никакое испарение уже невозможно.

Перрен сперва поставил свою кюветку набок и стал смотреть на нее в микроскоп. В поле зрения микроскопа оказалась тонкая вертикальная водяная стенка, внутри которой распределялись участвующие в брауновском движении зернышки гуммигута. Распределение зернышек сперва было однородным, но потом, с течением времени, распределение изменилось и в конце концов стало таким: очень много зернышек внизу, а по мере продвижения вверх их становится все меньше и меньше (см. рисунок). Число зернышек в одном кубическом микроне уменьшается с увеличением высоты и притом по некоторому вполне определенному закону.

Этот закон уменьшения плотности эмульсии с высотой Перрен захотел исследовать. Для этого он положил кюветку на дно, и после того как частицы расположились по высоте подобно тому, как в кювете, стоящей вертикально, стал смотреть на кюветку сверху в микроскоп, имевший очень маленькую глубину поля зрения: в микроскоп было видно все, что происходит в тонком слое глубиной в один микрон. Передвигая микроскоп вверх и вниз, можно было помещать этот слой то выше, то ниже. Перрен стал работать так: поставил микроскоп на какой-то высоте и начал считать, сколько зернышек виднеется в поле зрения на этой высоте, затем передвинул микроскоп на новую высоту и снова сосчитал число зернышек и т. д. Заметим, что при этом числом зернышек считается среднее из нескольких наблюдений, потому что зернышки движутся совершенно хаотически и, следовательно, их число в поле зрения микроскопа бывает то больше, то меньше в зависимости от случая. Поэтому на одной и той же высоте Перрен производил подсчет зернышек много раз и затем уже вычислял значение, характерное для каждой такой высоты.

Фотографии гуммигутовой эмульсии, сделанные Ж. Перреном через микроскоп

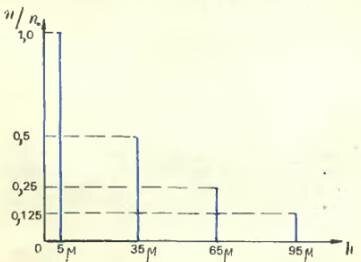
Приведем результаты одного из опытов Перрена. Глубина кюветки была, как мы уже говорили, 100 микрон (то есть 0,1 мм). Отсчеты производились на высотах 5, 35, 65 и 95 микрон над уровнем донышка кюветки. Оказалось, что среднее число частиц на высоте 35 микрон составляет половину того, которое было на высоте 5 микрон, число частиц на высоте 65 микрон было равно половине числа частиц на высоте 35 микрон, а число частиц на высоте 95 микрон равнялось половине числа частиц на высоте 65 микрон. Иными словами, при поднятии вверх на каждые 30 микрон число частиц в данном объеме (соответствующем глубине и ширине выбранного поля зрения) уменьшалось вдвое. Поэтому математический закон убывания плотности (числа частиц в данном объеме, а значит, и в каждой единице объема) с высотой может быть словами выражен так: если высоты образуют арифметическую прогрессию, то числа зерен образуют геометрическую прогрессию.

Результаты опытов Перрена

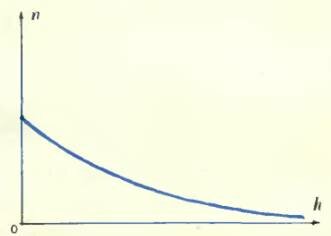
Такой закон убывания плотности зерен с высотой должен был сильно поразить и заинтересовать Перрена: ведь по такому же самому закону спадает плотность при поднятии в нашей атмосфере. Блэз Паскаль, знаменитый французский ученый, живший в XVII столетии и впервые применивший к изучению атмосферы барометр, изобретенный итальянцем Торричелли, обнаружил закон, по которому спадает с увеличением высоты плотность атмосферного воздуха. Этот закон, получивший название барометрической формулы, гласит то же самое: плотность каждого из газов, составляющих атмосферу, убывает вместе с увеличением высоты в геометрической прогрессии.

Так изменяется количество молекул воздуха с высотой

[Закон этот можно выразить и математически, в виде формулы.

Предположим, что на какой-то высоте h₀ над Землей в каждом кубическом сантиметре содержится n₀ молекул какого-то газа. На какой-то другой, большей высоте h таких же молекул в одном кубическом сантиметре будет, конечно, меньше, например n. Тогда барометрическая формула может быть записана в таком виде:

(~lg frac{n_0}{n} = Amg (h — h_0)) ^[1]. (1)

Здесь А — это некоторая постоянная величина, одинаковая для всех газов (при данной температуре), а m — масса молекулы того газа, о котором идет речь, g — ускорение силы тяжести.

Сразу видно, что в левой части равенства стоит отношение чисел частиц в единице объема (правда, под знаком логарифма), а в правой — разность высот. Это и означает, что если высоты образуют арифметическую прогрессию, то числа частиц образуют прогрессию геометрическую.

Выберем такую разность высот h — h₀, чтобы число частиц n на высоте h было вдвое меньше числа частиц n₀ на высоте h₀. Тогда формула (1) примет вид

(~lg 2 = Amg (h — h_0)) . (2)

В таблице логарифмов легко найти, что lg 2 = 0,30103, так что

(~0,30103 = Amg (h — h_0)) . (3)

Если бы было известно численное значение постоянной А, то, подсчитав число частиц в единице объема n и n₀ на высотах h и h₀, легко было бы вычислить и массу молекулы m, то есть взвесить ее. Правда, сосчитать молекулы мы тоже не можем, но ведь нам и не надо знать каждое из чисел n и n₀ в отдельности. Нужно знать только их отношение. А его легко найти, если измерить барометром давления на высотах h и h₀: отношение давлений как раз и равно отношению чисел частиц в единице объема. Но дело в том, что величина А во времена Перрена не была известна (именно опыты Перрена и позволили определить ее). Поэтому Перрен мог рассуждать так: известно, например, что] при поднятии на 5 км количество кислорода, находящегося в кубическом сантиметре, уменьшается вдвое; при поднятии на следующие 5 км оно уменьшается еще вдвое и т. д. и т. д. Это — тот же закон, по которому уменьшается с высотой число зернышек гуммигута в кубическом сантиметре эмульсии, но только здесь иные масштабы — вместо 30 микрон здесь мы имеем 5 км. Отчего же здесь получаются другие масштабы?

Слой гуммигутовой эмульсии в 100 микрон — это, в сущности, такая .же атмосфера, но только состоящая не из молекул кислорода или азота, а из зернышек гуммигута, которые уже достаточно велики, чтобы их можно было видеть в микроскоп. Вследствие большей массы этих зернышек (по сравнению с молекулами газа) уменьшение плотности с высотой происходит быстрее, чем в обыкновенной атмосфере, окружающей нашу Землю, а именно (в случае гуммигутовых зернышек диаметром 0,21 микрона) плотность уменьшается вдвое при поднятии на 30 микрон. «Эмульсия,— говорит Перрен, — это атмосфера в миниатюре, тяготеющая к Земле. В масштабе такой атмосферы высота Альп представилась бы несколькими микронами, а отдельные холмы стали бы равны молекулам». Для нас всего важнее, что молекулы этой миниатюрной «атмосферы» — зернышки гуммигута — могут быть взвешены, а это . позволяет вычислить и массу молекул обыкновенного газа. Так Перрен сумел сделать то, что казалось совершенно невозможным, — взвесить молекулы и атомы.

[Из формулы (3) видно, что произведение массы молекулы m на разность высот, между которыми число молекул в единице объема изменяется вдвое, во всех случаях (то есть для любых частиц) равно одной и той же величине (~frac{0,30103}{A}).

Поэтому, если для гуммигутовых зерен разность высот меньше, чем для кислорода в атмосфере, то это потому, что масса гуммигутового зернышка больше массы молекулы кислорода и как раз во столько раз, во сколько раз 5 км больше, чем 30 микрон.]

Проделаем нехитрый расчет… 5 км в 166 миллионов раз больше, чем 30 микрон. Значит, масса гуммигутового зернышка с диаметром 0,21 микрона превышает массу кислородной молекулы в 166 миллионов раз.

Сколько же весит такой гуммигутовый шарик? Это нетрудно рассчитать, если измерить предварительно массу кубического сантиметра гуммигута. При этом расчете не следует забывать, что в опытах Перрена зернышки гуммигута находились в воде, а значит, по закону Архимеда каждый кубический сантиметр гуммигута терял в весе ровно столько, сколько весит кубический сантиметр воды, то есть 1 г. Значит, каждый кубический сантиметр гуммигута был в воде на один грамм легче, чем в воздухе. В результате всех расчетов (которые мы пропускаем) получается, что масса зернышка (с поправкой на закон Архимеда) была равна 8,5·10^-15 г. И она в 166 миллионов раз больше массы молекулы кислорода. Значит, масса молекулы кислорода равна 5,1·10^-23 г. А так как молекула кислорода в 32 раза тяжелее атома водорода (молекулярный вес кислорода равен 32), то масса атома водорода — этого самого легкого из всех атомов — равна 1,6·10^-24 г. В грамме водорода содержится, следовательно, 6·10²³ атомов.

[Так атомы и молекулы были не только взвешены, но и сосчитаны!]

Эти цифры, найденные Перреном, позволили связать употреблявшуюся в то время единицу атомного веса — массу атома водорода — с граммом. Масса атома водорода, выраженная в граммах, получилась настолько ничтожной, что ее никак невозможно себе представить, тем не менее она получилась вполне определенной. Атом был взвешен. Важнейшая задача атомной физики была решена.

[Заметим здесь, что цифры, полученные Перреном, конечно, не очень точны. Впоследствии были найдены другие способы определения масс атомов и молекул, и теперь мы располагаем более правильными значениями масс. По современным данным масса атома водорода, например, равна 1,673·10^-24 г, а молекулы кислорода — 5,314·10^-23 г. Как видите, эти цифры не так уж сильно отличаются от тех, что впервые были получены Перреном.]

Вот какой результат получил Перрен, изучая распределение зернышек гуммигута в гуммигутовой эмульсии в зависимости от высоты. Но всего любопытнее то обстоятельство, что точно такой же результат был выведен с помощью тех же гуммигутовых шариков, но совершенно иным путем, о котором мы также скажем несколько слов.

Брауновское движение

Брауновское движение в гуммигутовой эмульсии совершается необыкновенно быстро. Нет никакой возможности проследить за движением отдельного гуммигутового зернышка. Поэтому Перрен и не пытался этого делать, а поступал следующим образом: он отмечал на чертеже положение гуммигутового зернышка через определенные промежутки времени, например через каждые 30 секунд, и полученные точки соединял прямыми линиями (хотя на самом деле гуммигутовое зернышко за это время двигалось не по прямой, а по причудливой ломаной линии). Полученные рисунки дают возможность судить о беспорядочности, хаотичности брауновского движения вообще. Но Перрен делал эти рисунки не только для того, чтобы получить наглядную иллюстрацию к брауновскому движению. Его интересовала количественная сторона дела. Знаменитый Альберт Эйнштейн, который был тогда еще молодым человеком, написал (в 1905 — 1906 годах) замечательные работы, где он вывел формулу, определяющую для заданного промежутка времени среднее смещение гуммигутового зернышка относительно его первоначального положения в жидкости. Мы не станем здесь приводить эту замечательную формулу, заметим только, что в эту формулу входит величина, равная числу атомов водорода в одном грамме. Поэтому, сравнивая формулу Эйнштейна с рисунками Перрена, определяющими перемещение частицы за 30 секунд, можно вычислить эту величину. Так и сделал Перрен, и у него получилось, что число атомов водорода в одном грамме равно 6·10²³, то есть получилось такое же число, как и раньше.

Совпадение двух чисел, которые были получены совершенно различными способами, является лучшим доказательством правильности всех сделанных предположений. Значит; молекулы и атомы действительно существуют, а не только являются удобной для химиков выдумкой. Такое заключение вынуждены были сделать даже те, которые долго и упорно не хотели признавать существования атомов.

… Вековой спор между сторонниками и противниками атомов закончился, таким образом, победой сторонников атомной теории. И в настоящее время мы можем с уверенностью утверждать, что все вещи на свете — и вода, и камни, и растения, и животные, и воздух, и железо и т. д. и т. д.— все это состоит из мельчайших невидимых глазу атомов.

Задачи к статье

Пользуясь приведенными в статье данными, найдите, на какой высоте давление уменьшается вдвое. Воздух легче кислорода в отношении 28,8 : 32.
P₀ — давление воздуха на уровне моря, P₁ — на высоте h. Каково давление воздуха на высотах: 2h, 3h, nh? Считать, что температура воздуха и ускорение свободного падения не меняются с высотой, и поэтому постоянная А не зависит от высоты.
Найдите высоту над поверхностью Земли, где давление воздуха равно 0,25 и 0,125 атмосферного. Постройте кривую зависимости давления воздуха от высоты.

Ответы

5,55 км.
(~P_2 = P_1 left( frac{P_1}{P_0} right)) ,

(~P_3 = P_2 left( frac{P_1}{P_0} right) P_1 left( frac{P_1}{P_0} right)^2) ,

(~P_n = P_1 left( frac{P_1}{P_0} right)^{n — 1}) .
11,1 км; 16,65 км. Удобно воспользоваться результатом задачи 1. Давление пропорционально плотности воздуха.

Примечания

↑ Если k — это число «шагов», за которое мы поднимаемся на высоту h, а Δh — высота «шага», то (~h = h_0 + (k — 1) Delta h), а (~n = n_0 left( frac 1q right)^{k — 1}), где (~frac 1q) — знаменатель прогрессии, которую составляет плотность газа (q > 1). Из этих двух формул, исключив k, мы найдем, что

(~lg frac{n_0}{n} = frac{lg q}{Delta h} (h — h_0)) . (*)

Аналогичную формулу можно записать и для другого газа; величины, относящиеся к нему, мы снабдим штрихом:

(~lg frac{n’_0}{n’} = frac{lg q’}{Delta h’} (h’ — h’_0)) . (**)

Очень важным оказывается то обстоятельство, что, если плотности первого и второго газов уменьшились в одно и то же число раз, то есть (~frac{n_0}{n} = frac{n’_0}{n’}), то отношение разностей высот, при которых это произошло, (~frac{h — h_0}{h’ — h’_0}) в точности равно обратному отношению масс молекул этих газов:

(~frac{h — h_0}{h’ — h’_0} = frac{m’}{m}) .

Разделим почленно уравнение (*) на уравнение (**):

(~1 = frac{lg q (h — h_0)Delta h’}{lg q’ (h’ — h’_0)Delta h} ) , или

(~frac{lg q}{lg q’} = frac{Delta h m}{Delta h’ m’} ) .

Таким образом, (~lg q sim Delta h m). Это дает возможность записать, что

(~lg q = A_1 Delta h m) .

где A₁ — это некоторая постоянная величина, не зависящая от величины шага и одинаковая для всех газов (при данной температуре).

Теперь барометрическую формулу (*) мы можем записать в таком виде:

(~lg frac{n_0}{n} = A_1mg (h — h_0)) .

Источник

АТОМНАЯ МАССА. Понятие об этой величине претерпевало длительные изменения в соответствии с изменением представления об атомах. Согласно теории Дальтона (1803), все атомы одного и того же химического элемента идентичны и его атомная масса – это число, равное отношению их массы к массе атома некоего стандартного элемента. Однако примерно к 1920 стало ясно, что элементы, встречающиеся в природе, бывают двух типов: одни действительно представлены идентичными атомами, а у других атомы имеют одинаковый заряд ядра, но разную массу; такие разновидности атомов были названы изотопами. Определение Дальтона, таким образом, справедливо только для элементов первого типа. Атомная масса элемента, представленного несколькими изотопами, есть средняя величина из массовых чисел всех его изотопов, взятых в процентном отношении, отвечающем их распространенности в природе.

В 19 в. в качестве стандарта при определении атомных масс химики использовали водород или кислород. В 1904 за стандарт была принята 1/16 средней массы атома природного кислорода (кислородная единица) и соответствующая шкала получила название химической. Масс-спектрографическое определение атомных масс проводилось на основе 1/16 массы изотопа ¹⁶О, и соответствующая шкала называлась физической. В 1920-х годах было установлено, что природный кислород состоит из смеси трех изотопов: ¹⁶О, ¹⁷О и ¹⁸О. В связи с этим возникли две проблемы. Во-первых, оказалось, что относительная распространенность природных изотопов кислорода немного варьирует, а значит, в основе химической шкалы лежит величина, не являющаяся абсолютной константой. Во-вторых, у физиков и химиков получались разные значения таких производных констант, как молярные объемы, число Авогадро и др. Решение вопроса было найдено в 1961, когда за атомную единицу массы (а.е.м.) была принята 1/12 массы изотопа углерода ¹²С (углеродная единица). (1 а.е.м., или 1D (дальтон), в СИ-единицах массы составляет 1,66057Ч10^–27 кг.) Природный углерод также состоит из двух изотопов: ¹²С – 99% и ¹³С – 1%, но новые величины атомных масс элементов связаны только с первым из них. В результате была получена универсальная таблица относительных атомных масс. Изотоп ¹²С оказался удобным и для физических измерений.

МЕТОДЫ ОПРЕДЕЛЕНИЯ

Атомную массу можно определить либо физическими, либо химическими методами. Химические методы отличаются тем, что на одном из этапов в них фигурируют не сами атомы, а их комбинации.

Химические методы.

Согласно атомной теории, числа атомов элементов в соединениях относятся между собой как небольшие целые числа (закон кратных отношений, который открыт Дальтоном). Поэтому для соединения известного состава можно определить массу одного из элементов, зная массы всех других. В некоторых случаях массу соединения можно измерить непосредственно, но обычно ее находят косвенными методами. Рассмотрим оба этих подхода.

Атомную массу Al недавно определили следующим образом. Известные количества Al были превращены в нитрат, сульфат или гидроксид и затем прокалены до оксида алюминия (Al₂O₃), количество которого точно определяли. Из соотношения между двумя известными массами и атомными массами алюминия и кислорода (15,9)

нашли атомную массу Al. Однако прямым сравнением с атомной массой кислорода можно определить атомные массы лишь немногих элементов. Для большинства элементов их определяли косвенным путем, анализируя хлориды и бромиды. Во-первых, эти соединения для многих элементов можно получить в чистом виде, во-вторых, для их точных количественных определений в распоряжении химиков имеется чувствительный аналитический метод, основанный на сравнении их масс с массой серебра. Для этого точно определяют массу анализируемых соединений и массу серебра, необходимого для взаимодействия с ними. Атомную массу нужного элемента рассчитывают исходя из атомной массы серебра – эталонной величины в подобных определениях. Атомную массу серебра (107,870) в углеродных единицах определяли косвенным химическим методом.

Физические методы.

В середине 20 в. существовал только один физический метод определения атомных масс, сегодня наиболее широко применяют четыре.

Плотность газа.

Самый первый физический метод основывался на определении плотности газа и на том, что в соответствии с законом Авогадро равные объемы газов при одинаковых температуре и давлении содержат одинаковое число молекул. Следовательно, если определенный объем чистого СО₂ имеет массу, в 1,3753 большую, чем такой же объем кислорода в тех же условиях, то молекула СО₂ должна быть в 1,3753 раза тяжелее молекулы кислорода (мол. масса О₂ = 31,998), т.е. масса молекулы СО₂ по химической шкале равна 44,008. Если из этой величины вычесть массу двух атомов кислорода, равную 31,998, мы получим атомную массу углерода – 12,01. Чтобы получить более точное значение, необходимо ввести ряд поправок, что усложняет этот метод. Тем не менее с его помощью были получены некоторые весьма ценные данные. Так, после открытия благородных газов (He, Ne, Ar, Kr, Xe) метод, основанный на измерении плотности, оказался единственно пригодным для определения их атомных масс.

Масс-спектроскопия.

Вскоре после Первой мировой войны Ф.Астон создал первый масс-спектроскоп для точного определения массовых чисел различных изотопов и тем самым открыл новую эру в истории определения атомных масс. Сегодня существует два основных типа масс-спектроскопов: масс-спектрометры и масс-спектрографы (последним является, например, прибор Астона). Масс-спектрограф предназначен для изучения поведения потока электрически заряженных атомов или молекул в сильном магнитном поле. Отклонение заряженных частиц в этом поле пропорционально отношению их масс к заряду, а регистрируют их в виде линий на фотопластинке. Сравнивая положения линий, отвечающих определенным частицам, с положением линии для элемента с известной атомной массой, можно с достаточной точностью определить атомную массу нужного элемента. Хорошей иллюстрацией метода является сравнение массы молекулы СН₄ (метана) с массовым числом самого легкого изотопа кислорода ¹⁶О. Одинаково заряженные ионы метана и ¹⁶О одновременно впускают в камеру масс-спектрографа и регистрируют их положение на фотопластинке. Различие в положении их линий отвечает разности масс 0,036406 (по физической шкале). Это значительно более высокая точность, чем может дать любой химический метод.

Если исследуемый элемент не имеет изотопов, то определение его атомной массы не составляет особого труда. В противном случае необходимо определить не только массу каждого изотопа, но и их относительное содержание в смеси. Эту величину не удается определить с достаточной точностью, что ограничивает применение масс-спектрографического метода для нахождения атомных масс изотопических элементов, особенно тяжелых. Недавно с помощью масс-спектрометрии удалось установить с высокой точностью относительное содержание двух изотопов серебра, ¹⁰⁷Ag и ¹⁰⁹Ag. Измерения были выполнены в Национальном бюро стандартов США. Используя эти новые данные и более ранние измерения масс изотопов серебра, уточнили значение атомной массы природного серебра. Теперь эта величина считается равной 107,8731 (химическая шкала).

Ядерные реакции.

Для определения атомных масс некоторых элементов можно использовать соотношение между массой и энергией, полученное Эйнштейном. Рассмотрим реакцию бомбардировки ядер ¹⁴N быстрыми ядрами дейтерия с образованием изотопа ¹⁵N и обычного водорода ¹Н:

¹⁴N + ²H = ¹⁵N + ¹H + Q

В результате реакции выделяется энергия Q = 8 615 000 эВ, которая в соответствии с уравнением Эйнштейна эквивалентна 0,00948 а.е.м. Значит, масса ¹⁴N + ²H превышает массу ¹⁵N + ¹H на 0,00948 а.е.м., и если мы знаем массовые числа трех любых изотопов – участников реакции, то можем найти массу четвертого. Метод позволяет определить разность массовых чисел двух изотопов с большей точностью, чем масс-спектрографический.

Рентгенография.

Этим физическим методом можно определять атомные массы веществ, которые при обычной температуре образуют регулярную кристаллическую решетку. Метод основан на связи между атомной (или молекулярной) массой кристаллического вещества, его плотностью, числом Авогадро и неким коэффициентом, который определяют из расстояний между атомами в кристаллической решетке. Необходимо провести прецизионные измерения двух величин: постоянной решетки рентгенографическими методами и плотности методом пикнометрии. Применение метода ограничивается трудностями получения чистых совершенных кристаллов (без вакансий и дефектов любого рода).

Уточнение атомных масс.

Все измерения атомных масс, которые были выполнены более 20 лет назад, проводились химическими методами или методом, основанным на определении плотности газов. В последнее же время данные, получаемые масс-спектрометрическими и изотопными методами, совпадают с такой высокой точностью, что Международная комиссия по атомным массам решила скорректировать атомные массы 36 элементов, причем 18 из них не имеют изотопов.
См. также АВОГАДРО ЧИСЛО.

Источник