Масса сплошной детали
Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем 

Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой 
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
1. Масса параллелепипеда (бруска)





Тогда масса:
2. Масса цилиндра




Тогда масса:
3. Масса шара



Тогда масса:
4. Масса сегмента шара




Тогда масса:
5. Масса конуса




Для круглого конуса: 


Масса круглого конуса:
6. Масса усеченного конуса










Отсюда масса:
7. Масса пирамиды




Для пирамиды с прямоугольным основанием: 



Тогда масса пирамиды:
8. Масса усеченной пирамиды






Исчеркав половину тетрадного листа, получаем: 





И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: 
Тогда масса усеченной прямоугольной пирамиды:
или
Для пирамиды с квадратным основанием (

Для того чтобы определить плотность вещества, надо массу тела разделить на его объем:
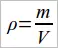
Массу тела можно определить с помощью весов. А как найти объем тела?
Если тело имеет форму прямоугольного параллелепипеда (рис. 24), то его объем находится по формуле
V = аbс.
Если же у него какая-то другая форма, то его объем можно найти методом, который был открыт древнегреческим ученым Архимедом в III в. до н. э.
Архимед родился в Сиракузах на острове Сицилия. Его отец, астроном Фидий, был родственником Гиерона, ставшего в 270 г. до н. э. царем города, в котором они жили.
До нас дошли не все сочинения Архимеда. О многих его открытиях стало известно благодаря более поздним авторам, в сохранившихся трудах которых описываются его изобретения. Так, например, римский архитектор Витрувий (I в. до н. э.) в одном из своих сочинений рассказал следующую историю:
«Что касается Архимеда, то изо всех его многочисленных и разнообразных открытий то открытие, о котором я расскажу, представляется мне сделанным с безграничным остроумием.
Во время своего царствования в Сиракузах Гиерон после благополучного окончания всех своих мероприятий дал обет пожертвовать в какой-то храм золотую корону бессмертным богам. Он условился с мастером о большой цене за работу и дал ему нужное по весу количество золота. В назначенный день мастер принес свою работу царю, который нашел ее отлично исполненной; после взвешивания вес короны оказался соответствующим выданному весу золота.
После этого был сделан донос, что из короны была взята часть золота и вместо него примешано такое же количество серебра. Гиерон разгневался на то, что его провели, и, не находя способа уличить это воровство, попросил Архимеда хорошенько подумать об этом. Тот, погруженный в думы по этому вопросу, как-то случайно пришел в баню и там, опустившись в ванну, заметил, что из нее вытекает такое количество воды, каков объем его тела, погруженного в ванну. Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)».
Затем, пишет Витрувий, Архимед взял сосуд, доверху наполненный водой, и опустил в него золотой слиток, равный по весу короне. Измерив объем вытесненной воды, он снова наполнил сосуд водой и опустил в него корону. Объем воды, вытесненной короной, оказался больше объема воды, вытесненной золотым слитком. Больший объем короны означал, что в ней присутствует менее плотное, чем золото, вещество. Поэтому опыт, проделанный Архимедом, показал, что часть золота была похищена.
Итак, для определения объема тела, имеющего неправильную форму, достаточно измерить объем воды, вытесняемой данным телом. Располагая измерительным цилиндром (мензуркой), это сделать несложно.
В тех случаях, когда известны масса и плотность тела, его объем можно найти по формуле, вытекающей из формулы (10.1):
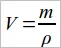
Отсюда видно, что для определения объема тела надо массу этого тела разделить на его плотность.
Если, наоборот, объем тела известен, то, зная, из какого вещества оно состоит, можно найти его массу:
m = ρV. (10.3)
Чтобы определить массу тела, надо плотность тела умножить на его объем.
1. Какие способы определения объема вы знаете? 2. Что вам известно об Архимеде? 3. Как можно найти массу тела по его плотности и объему?
Экспериментальное задание. Возьмите кусок мыла, имеющий форму прямоугольного параллелепипеда, на котором обозначена его масса. Проделав необходимые измерения, определите плотность мыла.
Масса прямоугольного параллелепипеда Калькулятор
| Search | ||
| Дом | физика ↺ | |
| физика | Инженерная механика ↺ | |
| Инженерная механика | Свойства поверхностей и тел ↺ | |
| Свойства поверхностей и тел | Массовый момент инерции ↺ |
|
✖Плотность материала показывает плотность этого материала в определенной заданной области. Это берется как масса на единицу объема данного объекта.ⓘ Плотность [ρ] |
+10% -10% |
||
|
✖Длина — это измерение или протяженность чего-либо от конца до конца.ⓘ Длина [L] |
+10% -10% |
||
|
✖Высота — это расстояние между самой низкой и самой высокой точками человека/фигуры/объекта, стоящего прямо.ⓘ Высота [H] |
+10% -10% |
||
|
✖Ширина — это измерение или протяженность чего-либо из стороны в сторону.ⓘ Ширина [w] |
+10% -10% |
|
✖Масса – это количество вещества в теле независимо от его объема или действующих на него сил.ⓘ Масса прямоугольного параллелепипеда [M] |
⎘ копия |
Масса прямоугольного параллелепипеда Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Плотность: 997 Килограмм на кубический метр —> 997 Килограмм на кубический метр Конверсия не требуется
Длина: 3 метр —> 3 метр Конверсия не требуется
Высота: 1.05 метр —> 1.05 метр Конверсия не требуется
Ширина: 0.7 метр —> 0.7 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
2198.385 Килограмм —> Конверсия не требуется
7 Массовый момент инерции Калькуляторы
Масса прямоугольного параллелепипеда формула
масса = Плотность*Длина*Высота*Ширина
M = ρ*L*H*w
Что такое масса?
Масса — одна из фундаментальных величин в физике. Масса — это мера количества вещества в теле. Чем больше масса тела, тем меньше изменение, вызванное приложенной силой.
Онлайн-калькулятор плотности, который поможет вам определить соотношение между плотностью, массой и весом объекта с помощью формулы плотности. В этом калькуляторе есть небольшая, но очень важная опция, где вы можете легко определить плотность объекта по категории и названию материала. Если вы хотите получить краткие сведения о том, как рассчитать плотность по формуле, продолжайте читать!
Кроме того, вы можете попробовать наш онлайн-калькулятор импульса, который поможет вам найти импульс движущегося объекта, а также определить массу объекта.
Читать дальше!
Что такое формула плотности?
Расчеты не слишком сложные, а очень простые. Просто введите значения в следующее уравнение плотности, чтобы легко вычислить любую из требуемых переменных:
р = м / В
Где,
V – объем & m – масса объекта.
Если вы хотите найти объем с помощью плотности и массы, калькулятор плотности использует формулу:
V = м / п
Чтобы найти массу с плотностью и объемом, рассмотрите следующую формулу:
т = р * V
Плотность можно определить как массу на единицу объема объекта. Со значениями введите единицы измерения, и этот калькулятор выполнит преобразование единиц измерения.
§ 2 Решение задач Какова масса подсолнечного масла в бутылке объемом 3 л, если плотность масла равна 930 кг/м3?
Запишем условие задачи. Нам известны объем бутылки (обозначается буквой V) 3 л, и плотность подсолнечного масла (обозначается буквой ρ) 930 кг/м3. Выразим объем бутылки в Международной системе единиц. 1 л = 0,001 м3, следовательно, 3 л составляют 0,003 м3.
Решение: Чтобы найти массу тела, нужно плотность умножить на объем: m = ρ · V. Подставим числовые значения величин: 930 кг/м3 · 0,003 м3 = 2,79 кг.
Сколько штук строительного кирпича размером 250 мм х 120 мм х 65 мм допускается перевозить на автомашине грузоподъемностью 4 т? Плотность кирпича 1800 кг/м3.
Запишем условие задачи и выразим данные в Международной системе единиц. Известны размеры кирпича: длина а = 250 мм = 0,25 м, ширина b= 120 мм = 0,12 м, высота с = 60 мм = 0,06 м, плотность кирпича ρ = 1800 кг/м3, грузоподъемность – наибольшая масса груза, которую может перевезти автомобиль – m = 4 т = 4000 кг. Найти количество кирпичей – обозначим латинской буквой N.
Решение: Количество кирпичей можно найти, поделив общую массу всех кирпичей на массу одного кирпича: N = m/m1. Чтобы найти массу одного кирпича, нужно плотность умножить на его объем: m1 = ρ · V. Кирпич имеет форму прямоугольного параллелепипеда, следовательно, его объем равен произведению длины, ширины и высоты кирпича. Подставим числовые значения известных величин и вычислим. Объем кирпича равен 0,0018 м3. Масса одного кирпича m1 равна 1800 кг/м3 , умножим на 0,0018 м3 , равно 3,24 кг. Тогда число кирпичей равно N 4000 кг, разделим на 3,24 кг и получим 1234, 567 штук или число целых кирпичей 1234 штуки.
Медный шар имеет массу 840 г при объеме 120 см3. Сплошной этот шар или полый? Плотность меди 8900 кг/м3.
Запишем условие задачи. Известна масса шара m 840 г, что в системе СИ составляет 0,84 кг, объем шара V=120 см3, в СИ 0,00 012 м3, плотность меди ρ = 8900 кг/м3. Определить, сплошной шар или содержит внутри пустое пространство?
Решение. Представим, что на рычажных весах лежат два медных шара, один сплошной, второй содержит внутри пустое пространство, то есть полый шар. Если у них массы одинаковы, то объем полого шара должен быть больше, чем объем сплошного шара (рис 1).
Определим, каков объем шара, состоящего полностью из меди. Если объем окажется равным 120 см3, то шар сплошной и пустот не содержит. Если же вычисленный объем окажется меньше 120 см3, значит, внутри есть полость.
Чтобы найти объем сплошного медного шара, массу шара разделим на его плотность. Для упрощения проведем вычисления в граммах и кубических сантиметрах.
Какая плотность воды?
Плотность воды между 0 ° C и 4 ° C обычно составляет 100 кг / м3, но она меняется в зависимости от температуры. При повышении температуры объем материала увеличивается. Согласно формуле, объем и плотность обратно пропорциональны друг другу, в конечном итоге плотность материала уменьшается. Плотность воды при различных температурах приведена в следующей таблице:
Стол
Ниже приведена таблица единиц, в которой плотность обычно выражается плотностями некоторых материалов.
Столы
Понятие объема тела
Объем является физическим свойством материи, которое определяет занимаемое ею пространство. В Международной системе единиц он измеряется в метрах кубических, но также часто используют другие единицы измерения: кубические сантиметры и литры.
В зависимости от состояния вещества применяют различные методы измерения объема:
- Для жидких тел используют специальные градуированные прозрачные емкости (цилиндры, пробирки, пипетки и другие).
- Для твердых тел, которые сохраняют свою форму, объем измеряется исходя из их линейных размеров с применением соответствующей математической формулы. Например, параллелепипеда объем равен произведению его длины, ширины и высоты.
- Газообразные тела не сохраняют свой объем, в отличие от жидкостей и твердых тел, поэтому он для газов всегда равен объему сосуда, в котором находится газ.
Как пользоваться калькулятором плотности:
Следуйте данным инструкциям по расчету с помощью этого онлайн-инструмента. С помощью этого калькулятора вы можете производить расчеты в простом и продвинутом режимах. Давайте взглянем!
Входы:
- Прежде всего, выберите во вкладке то, что вам нужно найти.
- Затем введите значения во все обозначенные поля в соответствии с выбранной опцией.
- Наконец, нажмите кнопку “Рассчитать”.
Выходы:
Как только вы заполните все поля, калькулятор покажет:
- Плотность объекта
- Масса объекта
- Объем объекта
- Корень кубический из объема
Заметка:
Есть дополнительное поле, где вы можете ввести категорию материала и название материала, этот калькулятор найдет плотность выбранного материала. Если вы не знаете значение объема, используйте предварительный вариант этого калькулятора для расчета объема, в противном случае используйте простой режим.
Масса сплошной детали
Главная > Вычисление масс > Масса сплошной детали
9.05.2013 // Владимир Трунов
Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей): Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр. Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
Масса параллелепипеда (бруска)
Объем параллелепипеда: , где — длина, — ширина, — высота. Тогда масса:
Масса цилиндра
Объем цилиндра: , где — диаметр основания, — высота цилиндра. Тогда масса:
Масса шара
Объем шара: , где — диаметр шара. Тогда масса:
Масса сегмента шара
Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента. Тогда масса:
Масса конуса
Объем любого конуса: , где — площадь основания, — высота конуса. Для круглого конуса: , где — диаметр основания, — высота конуса. Масса круглого конуса:
Масса усеченного конуса
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем: , где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса. Отсюда масса:
Масса пирамиды
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды. Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды. Тогда масса пирамиды:
Масса усеченной пирамиды
Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , . Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды. И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: . Тогда масса усеченной прямоугольной пирамиды:
или
Для пирамиды с квадратным основанием (, ) формула выглядит проще:
вычисление массы
-
Масса проволоки, прутка, проката
-
Масса кольца, звена
-
Масса полой детали
Похожие записи
Связь между объемом и массой для воды
Чтобы объем воды перевести в массу, следует воспользоваться приведенной выше формулой. Однако для чистой воды значение плотности составляет 1000 кг/м3, или 1 г/см3, или 1 кг/л. Это означает, что объем в массу и наоборот для этой субстанции легко переводить, для этого нужно лишь знать соответствие между единицами измерений этих физических величин. Например, 2 л воды имеют массу 2 кг, а 3,5 тонны воды занимают объем 3,5 м3.
Отметим, что плотность 1000 кг/м3 характерна только для чистой воды. Любые примеси и соли могут значительно изменить этот показатель, например плотность морской воды составляет 1027 кг/м3, то есть морская вода на 2,7 % плотнее пресной.
Физическая величина плотность
Наконец, прежде чем переходить к вопросу о том, как перевести объем в массу, рассмотрим плотность — величину, которая непосредственно касается указанного вопроса.
В таких науках, как химия и физика, под плотностью некоторой субстанции понимают количество массы, которая заключена в определенном объеме. Поскольку объем и масса являются скалярными величинами, то и плотность также — скаляр. Обычно плотность обозначают греческой буквой ρ (ро).
Согласно приведенному определению, математически можно записать: ρ = m/V, где m — масса тела в килограммах, V — объем в кубических метрах, который занимает это тело. Это означает, что плотность измеряется в единицах кг/м3.
Как найти массу в физике через объем и плотность?
Перейдем теперь непосредственно к решению поставленной задачи. Допустим необходимо измерить массу имеющегося алмаза. Сначала нужно измерить его объем, допустим, он равен 5000 см3. Разбираясь в том, как найти массу через объем, следует также определить плотность вещества. В данном случае можно обратиться к табличным данным и посмотреть, какая плотность характерна для алмаза. В таблице находим, что она равна 3,52 г/см3.
После того как все необходимые величины определены, следует использовать известную формулу, как найти массу через объем и плотность: m = V*ρ, где V — объем тела, ρ — плотность. Подставляя полученные значения для алмаза, получаем: m = 5000 (см3)*3,52 (г/см3) = 17600.0 г = 17,6 кг. Следует обратить внимание, что при умножении объема на плотность единицы измерения объема (см3 в примере) сокращаются и остаются только единицы измерения массы.
Плотность вещества
Наконец, отвечая на вопрос о том, как найти массу через объем и плотность, следует разобраться с последней характеристикой — плотностью тел. Плотность является неотъемлемой физической характеристикой материи, которая связывает массу и объем, то есть она определяет, какое количество массы вещества содержится в единице объема. В Международной системе единиц она выражается в виде килограммов на метр кубический, но часто используется и в граммах на сантиметр кубический.
Любое вещество обладает конкретным значением плотности, например, в одном литре воды содержится один килограмм массы, то есть ее плотность равна 1 кг/л или 1000 кг/м3.
Понятие плотности играет важную роль в природе. Так, вопрос плавучести тел в воде является исключительно вопросом сравнения плотности тела и воды. Тела, имеющие большую плотность, чем вода, тонут в ней, например, яйцо или камень.
Считаем вес листового проката
Самый простой вариант – листовой стальной прокат.
Определение! Во всех наших расчётах базовой величиной является усреднённая плотность стали – 7 850 кг/м3 по системе СИ.
Проведём для начала несложное действие – узнаем массу квадратного метра стального листа толщиной 1 мм. Выглядит это так – 1 м х 1 м х 0,001 м х 7850 кг/м3. То есть, мы перемножили длину, ширину и толщину листа (все величины взяли в метрах), и получили объём изделия. Произведение объёма и плотности даёт массу – 7,85 кг. Таким образом, мы выяснили, что метр квадратный стального листа толщиной 1 мм весит 7,85 кг.
А далее все вычисления производят умножением величины 7,85 кг на площадь и толщину реального листа. Например, вам надо купить лист толщиной 4 мм и площадью 2 м2. Массу такого изделия определяют по формуле 7,85х4х2= 62,8 кг. Лист такого же размера, но толщиной 2 мм весит 7,85х2х2=31,4 кг.
Если вас устраивает приблизительный расчёт – округлите значение 7,85 кг до 8 кг. Тогда вычисления можно проводить даже в уме без калькулятора, а погрешность составит менее 2%.
Приведём веса стальных листов наиболее популярных размеров.
| Толщина листа, мм | Размеры листа, м | Вес листа, кг | Вес 1 м2, кг |
| 0,35 | 1,0х2,0 | 5,5 | 2,75 |
| 0,35 | 1,25х2,5 | 8,59 | |
| 0,5 | 1,0х2,0 | 7,85 | 3,93 |
| 0,5 | 1,25х2,5 | 12,27 | |
| 0,8 | 1,0х2,0 | 12,56 | 6,28 |
| 0,8 | 1,25х2,5 | 19,63 | |
| 1,0 | 1,0х2,0 | 15,7 | 7,85 |
| 1,0 | 1,25х2,5 | 24,53 | |
| 1,5 | 1,0х2,0 | 23,55 | 11,78 |
| 1,5 | 1,25х2,5 | 36,8 | |
| 2,0 | 1,0х2,0 | 31,4 | 15,7 |
| 2,0 | 1,25х2,5 | 49,06 | |
| 2,5 | 1,0х2,0 | 39,25 | 19,63 |
| 2,5 | 1,25х2,5 | 61,33 | |
| 3,0 | 1,0х2,0 | 47,1 | 23,55 |
| 3,0 | 1,25х2,5 | 73,59 | |
| 3,5 | 1,25х2,5 | 85,86 | 27,48 |
| 4,0 | 1,5х6,0 | 282,6 | 31,4 |
| 5,0 | 1,5х6,0 | 353,25 | 39,25 |
Масса сплошной детали
Главная > Вычисление масс > Масса сплошной детали
9.05.2013 // Владимир Трунов
Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей): Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр. Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
Масса параллелепипеда (бруска)
Объем параллелепипеда: , где — длина, — ширина, — высота. Тогда масса:
Масса цилиндра
Объем цилиндра: , где — диаметр основания, — высота цилиндра. Тогда масса:
Масса шара
Объем шара: , где — диаметр шара. Тогда масса:
Масса сегмента шара
Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента. Тогда масса:
Масса конуса
Объем любого конуса: , где — площадь основания, — высота конуса. Для круглого конуса: , где — диаметр основания, — высота конуса. Масса круглого конуса:
Масса усеченного конуса
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем: , где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса. Отсюда масса:
Масса пирамиды
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды. Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды. Тогда масса пирамиды:
Масса усеченной пирамиды
Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , . Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды. И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: . Тогда масса усеченной прямоугольной пирамиды:
или
Для пирамиды с квадратным основанием (, ) формула выглядит проще:
вычисление массы
-
Масса обручального кольца
-
Масса полой детали
-
Масса пластины
Похожие записи
Что такое переводной коэффициент
Усложним задачу. Предположим, вам надо купить лист из цветного металла. Воспользуемся переводным коэффициентом, который представляет собой отношение плотности конкретного металла или сплава к усреднённому значению плотности стали. Путём умножения веса стального изделия определённого сортамента и размера на коэффициент нужного металла или сплава получаем вес детали.
| Наименование металла или сплава | Коэффициент |
| Алюминий | 0,34 |
| Медь | 1,14 |
| Латунь ЛС59 | 1,08 |
| Бронза ОЦС 5-5-5 | 1,12 |
| Чугун серый | 0,9 |
Пример – рассчитаем массу бронзового листа толщиной 2 мм и площадью 2 м2.
7,85х2х2х1,12 = 35,2 кг
Внимание! Этот же простой алгоритм можно применять и для неметаллических листовых материалов, для которых также существуют переводные коэффициенты. Например, для резины – 0,17-0,23, органического стекла – 0,15, капролона – 0,15, текстолита – 0,18, резины – 0,17-0,23.
Как узнать массу трубы
Для определения массы труб оптимально воспользоваться таблицами.
| Условный проход, дюйм/мм | Толщина стенки, мм | Вес, кг | Условный проход, дюйм/мм | Толщина стенки, мм | Вес, кг |
| 1/4 (8) | 2,35 | 0,65 | 11/4 (32) | 3,25 | 3,14 |
| 1/2 (15) | 2,65 | 1,22 | 11/2 (40) | 3,25 | 3,61 |
| 3/4 (20) | 2,65 | 1,58 | 2 (50) | 3,65 | 5,1 |
| 1 (25) | 3,25 | 2,44 | 21/2 (65) | 3,65 | 6,51 |
Если же доступа к справочным материалам нет, а несложные геометрические формулы не являются для вас препятствием, вычислите вес самостоятельно. Для этого находим разницу площади круга по внешнему радиусу и площади по внутреннему радиусу. Полученную разность умножаем на длину трубы и плотность стали – 7 850 кг/м3.
Для труб из цветных металлов применяют переводные коэффициенты, о которых мы говорили выше.
Плотность и объем
Как было отмечено, масса — это неотъемлемое свойство материи, поэтому ее можно вычислить с помощью других физических характеристик тел. Этими характеристиками являются объем и плотность.
Объем представляет собой некоторую часть пространства, которая ограничена поверхностью тела. Измеряется он в кубических единицах длины, например, в м3.
Плотность — это свойство вещества, которое отражает количество материи, помещенной в единице объема.
Формула массы вещества через объем и плотность записывается так:
m = ρ * V
Чем больше объем тела и чем выше его плотность, тем большей массой оно обладает. В связи с этим фактом полезно вспомнить знаменитую загадку про то, что имеет большую массу: 1 тонна пуха или 1 тонна железа. В отсутствии выталкивающей архимедовой силы массы обоих веществ равны. Пух имеет гораздо меньшую плотность, чем железо, однако разница в плотности компенсируется аналогичной разницей в объеме.
Как рассчитать массу равнополочного уголка, швеллера, двутавра
Масса метра погонного углового металлопроката зависит от ширины и толщины полок.
Внимание! Рассчитанный по геометрической формуле или определённый по таблице вес уголка может сильно отличаться от фактического. Это связано с тем, что некоторые производители в целях удешевления продукции снижают толщину полки уголка в местах, где не предусматриваются проверочные замеры. Такая разница может значительно превышать допуски, предусмотренные ГОСТом.
Вес погонного метра наиболее распространённого сортамента равнополочного уголка
| Ширина полки, мм | Толщина полки, мм | Вес 1 м уголка, кг | Ширина полки, мм | Толщина полки, мм | Вес 1 м уголка, кг |
| 20 | 3 | 0,89 | 40 | 3 | 1,85 |
| 20 | 4 | 1,15 | 40 | 4 | 2,42 |
| 25 | 3 | 1,12 | 45 | 3 | 2,08 |
| 25 | 4 | 1,46 | 45 | 4 | 2,73 |
| 32 | 3 | 1,46 | 50 | 3 | 2,32 |
| 32 | 4 | 1,91 | 50 | 4 | 3,05 |
| 36 | 3 | 1,65 | 63 | 4 | 3,9 |
| 36 | 4 | 2,16 | 63 | 5 | 4,81 |
Самостоятельно просчитать массу швеллера и двутавра затруднительно из-за сложной формы сечения. В данном случае пользуются таблицами.
Таблица весов швеллера
| Номер профиля | Вес 1 м, кг | Номер профиля | Вес 1 м, кг | Номер профиля | Вес 1 м, кг |
| 5 | 4,84 | 12 | 10,4 | 20 | 18,4 |
| 6,5 | 5,9 | 14 | 12,3 | 22 | 21,0 |
| 8 | 7,05 | 16 | 14,2 | 24 | 24 ,0 |
| 10 | 8,59 | 18 | 16,3 | 27 | 27,7 |
Таблица весов двутавра
| Номер профиля | Вес 1 м, кг | Номер профиля | Вес 1 м, кг | Номер профиля | Вес 1 м, кг |
| 10 | 9,46 | 18 | 18,4 | 27 | 31,5 |
| 12 | 11,5 | 20 | 21,0 | 30 | 36,5 |
| 14 | 13,7 | 22 | 24,0 | 33 | 42,2 |
| 16 | 15,9 | 24 | 27,3 | 36 | 48,6 |
Весы для измерения массы
Весы напольные, электронные, ручные, используемые для измерения массы тела в физике, откалиброваны специальным образом. Они показывают сразу килограммы. То есть, пересчитывают вес в массу по формуле, представленной в пункте выше. Вот так устроены эти приборы.
Другим способом измерения массы являются весы с двумя плечами рычага. Для определения рассматриваемой величины с помощью таких устройств используют набор эталонных гирь. Ими стараются уравновесить измеряемое тело.
Калькуляторы расчёта веса металла
Если у вас есть доступ к интернету – расчёты массы металлопроката не составляют никакого труда. Калькулятором металла можно пользоваться в режиме он-лайн или скачать его на компьютер.
Как выполняется расчёт:
- В списке выбирают тип металлопроката.
- Заполняют данные в размерности, указанной в программе.
- Нажимают кнопку расчёта.
- В калькуляторах также обычно указывают массу погонного метра конкретного сортамента и количество метров в тонне.
Внимание! Все данные, предоставляемые металлокалькуляторами, основаны на ГОСТ. При отсутствии табличных величин масса рассчитывается по геометрическим формулам с поправкой на особенности изготовления данных изделий. При стандартных подсчётах плотность стали принимается равной 7 850 кг/м3.
Реальная масса металлопроката практически всегда отличается от теоретической.
Формула для гравитации
Математическое описание явления гравитации стало возможным благодаря многочисленным наблюдениям за движением космических тел. Результаты всех этих наблюдений в XVII веке обобщил Исаак Ньютон в рамках закона всемирного тяготения. Согласно этому закону, два тела, которые имеют массы m1 и m2, друг к другу притягиваются с такой силой F:
F = G * m1 * m2 / r2
Где r — расстояние между телами, G — некоторая постоянная.
Если в данное выражение подставить значение массы нашей планеты и ее радиус, тогда мы получим следующую формулу массы в физике:
m = F / g
Здесь F — сила тяжести, g — ускорение, с которым тела падают на землю вблизи ее поверхности.
Как известно, наличие силы тяжести обуславливает то, что все тела имеют вес. Многие путают вес и массу, полагая, что это одна и та же величина. Обе величины действительно связаны через коэффициент g, однако вес — величина изменчивая (она зависит от ускорения, с которым движется система). Кроме того, вес измеряется в ньютонах, а масса в килограммах.
Весы, которыми человек пользуется в быту (механические, электронные), показывают массу тела, однако измеряют его вес. Перевод между этими величинами является лишь вопросом калибровки прибора.
Как пользоваться справочниками
Удобным справочным материалом является сборник авторов Поливанова П.М. и Поливановой Е.П. «Таблицы для подсчёта массы деталей и материалов». В справочнике представлены таблицы, позволяющие легко и быстро определить массу проката круглого, прямоугольного, шестиугольного сечений, листа и полосы, равнополочной и неравнополочной угловой стали, двутавра, швеллера, круглых и профильных труб.
В сборнике даны формулы, по которым можно рассчитать площади и объёмы геометрических фигур. Подробная таблица переводных коэффициентов позволяет точно подсчитать массу цветного металла или его сплава.
Приближёнными методиками расчётов можно воспользоваться только для предварительного определения массы материалов, изделий и конструкций. Для составления проектной документации применяют только точные данные, полностью соответствующие ГОСТ.
Определение и формула массы тела
В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и источником гравитационного взаимодействия. В классической физике масса всегда является положительной величиной.
Масса
– аддитивная величина, что означает: масса каждой совокупности материальных точек (m) равна сумме масс всех отдельных частей системы (mi):
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.