Содержание:
- § 1 Расчет массы и объема вещества по его плотности
- § 2 Решение задач
- § 3 Важно запомнить
§ 1 Расчет массы и объема вещества по его плотности
В этом уроке мы изучим, как можно определить массу и объем тела, если известна плотность вещества.
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Из формулы плотности следует, что масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: v = m : p.
Для правильного решения задач нужно уметь верно переводить единицы измерения величин в Международную систему единиц: 1 г = 0,001 кг, 1 л = 1 дм3 = 0,001 м3, 1 см3 = 0,000 001 м3, 1 г/см3 = 1000 кг/м3.
§ 2 Решение задач
Какова масса подсолнечного масла в бутылке объемом 3 л, если плотность масла равна 930 кг/м3?
Запишем условие задачи. Нам известны объем бутылки (обозначается буквой V) 3 л, и плотность подсолнечного масла (обозначается буквой ρ) 930 кг/м3. Выразим объем бутылки в Международной системе единиц. 1 л = 0,001 м3, следовательно, 3 л составляют 0,003 м3.
Решение: Чтобы найти массу тела, нужно плотность умножить на объем: m = ρ · V. Подставим числовые значения величин: 930 кг/м3 · 0,003 м3 = 2,79 кг.
Сколько штук строительного кирпича размером 250 мм х 120 мм х 65 мм допускается перевозить на автомашине грузоподъемностью 4 т? Плотность кирпича 1800 кг/м3.
Запишем условие задачи и выразим данные в Международной системе единиц. Известны размеры кирпича: длина а = 250 мм = 0,25 м, ширина b= 120 мм = 0,12 м, высота с = 60 мм = 0,06 м, плотность кирпича ρ = 1800 кг/м3, грузоподъемность – наибольшая масса груза, которую может перевезти автомобиль – m = 4 т = 4000 кг. Найти количество кирпичей – обозначим латинской буквой N.
Решение: Количество кирпичей можно найти, поделив общую массу всех кирпичей на массу одного кирпича: N = m/m1. Чтобы найти массу одного кирпича, нужно плотность умножить на его объем: m1 = ρ · V. Кирпич имеет форму прямоугольного параллелепипеда, следовательно, его объем равен произведению длины, ширины и высоты кирпича. Подставим числовые значения известных величин и вычислим. Объем кирпича равен 0,0018 м3. Масса одного кирпича m1 равна 1800 кг/м3 , умножим на 0,0018 м3 , равно 3,24 кг. Тогда число кирпичей равно N 4000 кг, разделим на 3,24 кг и получим 1234, 567 штук или число целых кирпичей 1234 штуки.
Медный шар имеет массу 840 г при объеме 120 см3. Сплошной этот шар или полый? Плотность меди 8900 кг/м3.
Запишем условие задачи. Известна масса шара m 840 г, что в системе СИ составляет 0,84 кг, объем шара V=120 см3, в СИ 0,00 012 м3, плотность меди ρ = 8900 кг/м3. Определить, сплошной шар или содержит внутри пустое пространство?
Решение. Представим, что на рычажных весах лежат два медных шара, один сплошной, второй содержит внутри пустое пространство, то есть полый шар. Если у них массы одинаковы, то объем полого шара должен быть больше, чем объем сплошного шара (рис 1).
Определим, каков объем шара, состоящего полностью из меди. Если объем окажется равным 120 см3, то шар сплошной и пустот не содержит. Если же вычисленный объем окажется меньше 120 см3, значит, внутри есть полость.
Чтобы найти объем сплошного медного шара, массу шара разделим на его плотность. Для упрощения проведем вычисления в граммах и кубических сантиметрах.
§ 3 Важно запомнить
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: V = m : p.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. — М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс — М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
Использованные изображения:
На прошлом уроке мы познакомились с определением плотности тела, узнали формулу, по которой можно ее рассчитать: $rho = frac{m}{V}$.
Сейчас нам предстоит взглянуть на эту формулу с других сторон. Мы научимся находить объем и массу по известной плотности материала тела, решать задачи, используя полученные знания.
Расчет массы тела по его плотности
Знание плотности веществ очень важно для многих практических целей. Для инженеров и строителей, например, знание плотности имеет колоссальное значение — так они могут рассчитать массу будущего механизма или строения.
Как вычисляется масса тела по его плотности и объему?
Плотность определяется по формуле $rho = frac{m}{V}$. Выразим отсюда массу:
$m = rho V$.
Чтобы рассчитать массу тела, если известны его объем и плотность, нужно плотность умножить на объем.
Задача на расчет массы
Рассмотрим пример задачи на расчет массы.
Рассчитайте массу детали, изготовленной из латуни, объемом $0.15 space м^3$.
Из таблицы 1 предыдущего урока берем значение плотности латуни. Она равна $8500 frac{кг}{м^3}$.
Дано:
$rho = 8500 frac{кг}{м^3}$
$V = 0.15 space м^3$
$m -?$
Показать решение и ответ
Скрыть
Решение:
$m = rho cdot V$,
$m = 8500 frac{кг}{м^3} cdot 0.15 space м^3 = 1275 space кг approx 1.3 space т$.
Ответ: $m = 1275 space кг approx 1.3 space т$.
Расчет объема тела по его плотности
По какой формуле можно определить объем тела?
Подобным образом выразим из формулы плотности объем:
$V = frac{m}{rho}$.
Чтобы рассчитать объем тела, если известны его масса и плотность, нужно массу разделить на плотность.
Данной формулой для определения объема часто пользуются в тех случаях, когда тела имеют сложную неправильную форму.
Задача на расчет объема
Рассмотрим пример задачи на расчет объема.
Молоко в бутылке имеет массу $1.03 space кг$. Рассчитайте объем бутылки.
В таблице 2 прошлого параграфа находим молоко: его плотность равна $1030 frac{кг}{м^3}$.
Дано:
$rho = 1030 frac{кг}{м^3}$
$m = 1.03 space кг$
$V -?$
Решение:
$V = frac{m}{rho}$,
$V = frac{1.03 space кг}{1030 frac{кг}{м^3}} = 0.001 space м^3 = 1 space л$.
Ответ: $V = 1 space л$.
Дополнительные задачи
Задача №1
На рисунке 1 изображен кусок хозяйственного мыла в упаковке. По данным производителя размеры размеры его полиэтиленовой упаковки составляют 6 см x 9 см x 5,5 см.
Масса одного куска 200 г. Масса брутто (масса товара вместе с упаковкой) указан 211 г. Найдите объем куска мыла без упаковки. Выразите ответ в СИ.
Обозначим стороны упаковки как $a, b space и space с$, массу куска была $m_м$, массу куска мыла в упаковке — $m$, а общую массу мыла в упаковке — $m_{уп}$.
Объем куска мыла будем обозначать как $V_м$, а вместе с упаковкой — $V$.
Дано:
$a = 6 space см$
$b = 9 space см$
$c = 5.5 space см$
$m_м = 200 space г$
$m = 211 space г$
$V_м -?$
Показать решение и ответ
Срыть
Решение:
Найдем массу упаковки:
$m_{уп} = m — m_м$,
$m_{уп} = 211 space г — 200 space г = 11 space г$.
Общий объем упаковки и мыла:
$V = a cdot b cdot c$,
$V = 6 space см cdot 9 space см cdot 5.5 space см = 297 space см^3$.
Указано, что упаковка изготовлена из полиэтилена (из таблицы 1 предыдущего параграфа его плотность $rho_п$ равна $0.92 frac{г}{см^3}$).
Найдем объем упаковки $V_{уп}$:
$V_{уп} = frac{m_{уп}}{rho_{уп}}$,
$V_{уп} = frac{11 space г}{0.92 frac{г}{см^3}} approx 12 space см^3$.
Общий объем куска мыла в упаковке складывается из объема самого куска и объема упаковки. Так мы можем найти объем куска мыла:
$V_м = V — V_{уп}$,
$V_м = 297 space см^3 — 12 space см^3 = 285 space см^3$.
Выразим в СИ:
$285 space см^3 = 285 cdot 1 space см cdot 1 space см cdot 1 space см = 285 cdot 0.01 space м cdot 0.01 space м cdot 0.01 space м = 285 cdot 0.000001 space м^3 = 0.000285 space м^3$.
Ответ: $V_м = 0.000285 space м^3$
Задача №2
Масса чугунного шара составляет 800 г. Его объем — $125 space см^3$. Будет ли этот шар сплошным (отлитым полностью из одного материала) или полым (иметь пространство внутри, заполненное, например, воздухом)?
Показать решение
Скрыть
Проверить это достаточно просто: рассчитаем плотность этого шара:
$rho = frac{m}{V}$,
$rho = frac{800 г}{125 space см^3} = 6.4 frac{г}{см^3}$.
Сравним полученное значение с табличной плотностью чугуна:
$rho = 7 frac{г}{см^3}$
Сколько бы тогда весил сплошной шар?
$m = rho V$,
$m = 7 frac{г}{см^3} cdot 125 space см^3 = 875 space г$.
Разница между массами реального и предполагаемого сплошного шара составляет 75 г.
Следовательно, реальный шар имеет внутри какую-то полость, он не полностью выполнен из чугуна.
Задача №3
В грузовой автомобиль загрузили 48 сосновых бревен. Масса каждого соснового бревна составляет $20 space дм^3$. На сколько увеличилась масса автомобиля после загрузки?
Из таблицы 1 предыдущего параграфа возьмем плотность сухой сосны ($400 frac{кг}{м^3}$). Переведем $20 space дм^3$ в $м^3$:
$20 space дм^3 = 20 cdot 0.1 space м cdot 0.1 space м cdot 0.1 space м = 20 cdot 0.001 space м^3 = 0.02 space м^3$.
Количество брусков — $n$.
Дано:
$V = 20 space дм^3$
$rho = 400 frac{кг}{м^3}$
$n = 48$
СИ:
$V = 0.02 space м^3$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем массу одного соснового бревна:
$m = rho cdot V$,
$m = 400 frac{кг}{м^3} cdot 0.02 space м^3 = 8 space кг$.
Масса всех сосновых бревен (M) будет равна:
$M = n cdot m$,
$M = 48 cdot 8 space кг = 384 space кг$
Ответ: масса автомобиля после загрузки увеличится на 384 кг.
Упражнения
Упражнение №1
Какова масса $0.5 space л$ спирта, молока, ртути?
Дано:
$V = 0.5 space л$
$rho_1 = 800 frac{кг}{м^3}$
$rho_2 = 1030 frac{кг}{м^3}$
$rho_3 = 13600 frac{кг}{м^3}$
СИ:
$V = 5 cdot 10^{-4} space м^3$
$m_1 — ?$
$m_2 — ?$
$m_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Зная объем и плотность тела, мы может рассчитать его массу по формуле: $m = rho V$.
Рассчитаем массу спирта:
$m_1 = rho_1 V$,
$m_1 = 800 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 0.4 space кг$.
Рассчитаем массу молока:
$m_2 = rho_2 V$,
$m_2 = 1030 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 0.515 space кг$.
Рассчитаем массу ртути:
$m_3 = rho_3 V$,
$m_3 = 13600 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 6.8 space кг$.
Ответ: $m_1 = 0.4 space кг$, $m_2 = 0.515 space кг$, $m_3 = 6.8 space кг$.
Упражнение №2
Определите объем льдинки, масса которой $108 space г$.
Дано:
$m = 108 space г$
$rho = 900 frac{кг}{м^3}$
СИ:
$m = 0.108 space кг$
$V — ?$
Показать решение и ответ
Скрыть
Решение:
Зная массу и плотность льда, рассчитаем его объем:
$V = frac{m}{rho}$,
$V = frac{0.108 space кг}{900 frac{кг}{м^3}} = 0.00012 space м^3 = 120 space см^3$.
Ответ: $V = 120 space см^3$.
Упражнение №3
Сколько килограммов керосина входит в пятилитровую бутыль?
Дано:
$V = 5 space л$
$rho = 800 frac{кг}{м^3}$
СИ:
$V = 5 cdot 10^{-3} space м^3$
$m — ?$
Показать решение и ответ
Скрыть
Решение:
Зная плотность и объем, найдем массу керосина:
$m = rho V$,
$m = 800 frac{кг}{м^3} cdot 5 cdot 10^{-3} space м^3 = 4 space кг$.
Ответ: $m = 4 space кг$.
Упражнение №4
Грузоподъемность лифта составляет $3 space т$. Сколько листов железа можно погрузить в лифт, если длина каждого листа равна $3 space м$, ширина — $60 space см$ и толщина — $4 space мм$?
Дано:
$M = 3 space т$
$a = 60 space см$
$b = 4 space мм$
$c = 3 space м$
$rho = 7800 frac{кг}{м^3}$
СИ:
$M = 3000 space кг$
$a = 0.6 space м$
$b = 0.004 space м$
$n — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем массу одного железного листа. Для этого нам нужно знать его объем (плотность мы взяли из таблицы). Объем мы может вычислить, перемножив друг на друга ширину, высоту и длину: $V = a cdot b cdot c$.
Масса железного листа:
$m = rho V = rho cdot a cdot b cdot c$,
$m = 7800 frac{кг}{м^3} cdot 0.6 space м cdot 0.004 space м cdot 3 space м = 56.16 space кг$.
Теперь разделим грузоподъемность лифта на массу одного лифта. Полученное целое число и будет ответом на вопрос задачи:
$n = frac{M}{m}$,
$n = frac{3000 space кг}{56.16 space кг} approx 53$.
Ответ: $n = 53$.
Упражнение №5
Кружка доверху наполнена молоком. Определите объем кружки, если масса молока в кружке $515 space г$, плотность молока найдите в таблице.
Дано:
$m = 515 space г$
$rho = 1030 frac{кг}{м^3}$
СИ:
$m = 0.515 space кг$
$V — ?$
Показать решение и ответ
Скрыть
Решение:
Зная массу и плотность молока, найдем объем, который оно занимает в кружке:
$V = frac{m}{rho}$,
$V = frac{0.515 space кг}{1030 frac{кг}{м^3}} = 0.0005 space м^3 = 0.5 space л$.
Ответ: $V = 0.5 space л$.
Задание
Возьмите баночку из-под меда. Рассмотрите внимательно этикетку. Найдите на ней, какова масса меда и объем баночки. Затем рассчитайте плотность меда. Полученный результат проверьте по таблице.
Дано:
$m = 800 space г$
$V = 500 space мл$
СИ:
$m = 0.8 space кг$
$V = 0.0005 space м^3$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем плотность меда:
$rho = frac{m}{V}$,
$rho = frac{0.8 space кг}{0.0005 space м^3} = 1600 frac{кг}{м^3}$.
По таблице плотность меда составляет $1350 frac{кг}{м^3}$. Существует множество различных сортов меда, плотность которых отличается друг от друга. Наше значение плотности не сильно отличается от табличного, поэтому можно сказать, что результат получен правильный.
Ответ: $rho = 1600 frac{кг}{м^3}$.
Для того чтобы определить плотность вещества, надо массу тела разделить на его объем:
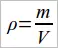
Массу тела можно определить с помощью весов. А как найти объем тела?
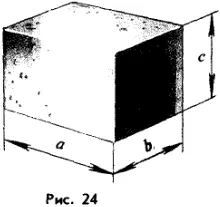
Если тело имеет форму прямоугольного параллелепипеда (рис. 24), то его объем находится по формуле
V = аbс.
Если же у него какая-то другая форма, то его объем можно найти методом, который был открыт древнегреческим ученым Архимедом в III в. до н. э.
Архимед родился в Сиракузах на острове Сицилия. Его отец, астроном Фидий, был родственником Гиерона, ставшего в 270 г. до н. э. царем города, в котором они жили.
До нас дошли не все сочинения Архимеда. О многих его открытиях стало известно благодаря более поздним авторам, в сохранившихся трудах которых описываются его изобретения. Так, например, римский архитектор Витрувий (I в. до н. э.) в одном из своих сочинений рассказал следующую историю:
«Что касается Архимеда, то изо всех его многочисленных и разнообразных открытий то открытие, о котором я расскажу, представляется мне сделанным с безграничным остроумием.
Во время своего царствования в Сиракузах Гиерон после благополучного окончания всех своих мероприятий дал обет пожертвовать в какой-то храм золотую корону бессмертным богам. Он условился с мастером о большой цене за работу и дал ему нужное по весу количество золота. В назначенный день мастер принес свою работу царю, который нашел ее отлично исполненной; после взвешивания вес короны оказался соответствующим выданному весу золота.
После этого был сделан донос, что из короны была взята часть золота и вместо него примешано такое же количество серебра. Гиерон разгневался на то, что его провели, и, не находя способа уличить это воровство, попросил Архимеда хорошенько подумать об этом. Тот, погруженный в думы по этому вопросу, как-то случайно пришел в баню и там, опустившись в ванну, заметил, что из нее вытекает такое количество воды, каков объем его тела, погруженного в ванну. Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)».
Затем, пишет Витрувий, Архимед взял сосуд, доверху наполненный водой, и опустил в него золотой слиток, равный по весу короне. Измерив объем вытесненной воды, он снова наполнил сосуд водой и опустил в него корону. Объем воды, вытесненной короной, оказался больше объема воды, вытесненной золотым слитком. Больший объем короны означал, что в ней присутствует менее плотное, чем золото, вещество. Поэтому опыт, проделанный Архимедом, показал, что часть золота была похищена.
Итак, для определения объема тела, имеющего неправильную форму, достаточно измерить объем воды, вытесняемой данным телом. Располагая измерительным цилиндром (мензуркой), это сделать несложно.
В тех случаях, когда известны масса и плотность тела, его объем можно найти по формуле, вытекающей из формулы (10.1):
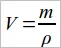
Отсюда видно, что для определения объема тела надо массу этого тела разделить на его плотность.
Если, наоборот, объем тела известен, то, зная, из какого вещества оно состоит, можно найти его массу:
m = ρV. (10.3)
Чтобы определить массу тела, надо плотность тела умножить на его объем.
1. Какие способы определения объема вы знаете? 2. Что вам известно об Архимеде? 3. Как можно найти массу тела по его плотности и объему?
Экспериментальное задание. Возьмите кусок мыла, имеющий форму прямоугольного параллелепипеда, на котором обозначена его масса. Проделав необходимые измерения, определите плотность мыла.
Масса тела

4.8
Средняя оценка: 4.8
Всего получено оценок: 70.
Обновлено 15 Июля, 2021
4.8
Средняя оценка: 4.8
Всего получено оценок: 70.
Обновлено 15 Июля, 2021
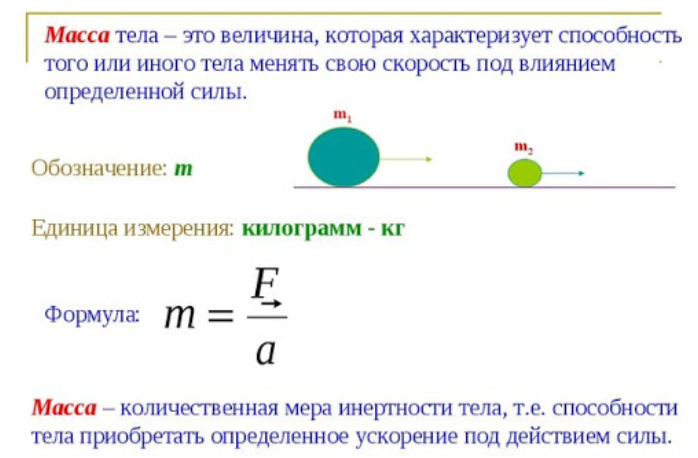
Одной из важнейших характеристик любого тела является его масса. Во многих физических законах и уравнениях масса тела играет одну из важнейших ролей, иногда совершенно меняя результат физического явления. Например, при равном объёме всплывание тела в одной и той же жидкости определяется исключительно массой. Поговорим о том, что это за величина, какие у неё свойства и особенности, на что влияет масса тела.
Масса тела
Для знакомства с физической природой массы проще всего провести опыт с телами одинаковой формы и размеров, но различной массы. Например, можно взять небольшой воздушный шарик, футбольный мяч и чугунное ядро тех же размеров (20—25 см диаметром).
Несмотря на одинаковые размеры, эти три тела при броске поведут себя совершенно по-разному. Воздушный шарик после удара по нему сразу приобретёт скорость, практически равную скорости руки. Но далее его скорость будет очень быстро уменьшаться из-за воздушного сопротивления. Футбольный мяч после удара пролетит гораздо дальше — на десятки метров. Но сообщить ему ту же начальную скорость, как воздушному шарику, будет труднее. Если же взять чугунное ядро, то силы мускулов хватит лишь на то, чтобы бросить его на пару метров.
Почему же в приведённых трёх примерах получается совершенно разный результат? Ответ заключается в разнице масс используемых предметов.
Данный опыт показывает, что для того, чтобы сообщить телу некоторую скорость, необходимо затратить усилия, и во время разгона тело будет «сопротивляться» разгону. Это «сопротивление разгону» называется инертностью тела. Физическая величина, характеризующая инертность, называется массой.
Свойства массы
Масса — это свойство любого материального объекта. Из-за наличия массы телам невозможно сообщить скорость мгновенно. Потребуется некоторое время, за которое тело наберёт скорость — тем большее, чем больше инертность тела, то есть чем большей массой оно обладает.
Масса также участвует в гравитационных взаимодействиях, она входит в формулу закона всемирного тяготения, учитывается в расчётах движения небесных тел. Неоднократные опыты доказывают эквивалентность инертной и гравитационной массы. Однако причина этого равенства — вопрос, открытый в современной физике.
Некоторые элементарные частицы не имеют массы. Это означает, что понятие «инертности» к ним неприменимо — их невозможно разогнать или замедлить. Сразу при рождении они движутся со скоростью света и двигаются без изменения скорости до поглощения или распада.
Единица измерения массы в СИ — килограмм (кг). Это базовая единица, то есть она не выводится из других, а сравнивается с некоторым эталоном. Изначально эталоном килограмма был вес воды объёмом 1 литр. Позже за эталон был принят специально изготовленный цилиндр диаметром и высотой 39,17 мм, сделанным из платино-иридиевого сплава. Сейчас килограмм определяется из фундаментальных физических констант (таких, как постоянная Планка, постоянная Больцмана).
Что мы узнали?
Любой материальный объект обладает инертностью, то есть для того чтобы изменить его скорость, требуется некоторое время и силы. Мера инертности — это масса. Масса также участвует в гравитационном взаимодействии. Измеряется масса в килограммах.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.8
Средняя оценка: 4.8
Всего получено оценок: 70.
А какая ваша оценка?