1. Запись
величин с учетом погрешности: ,
где А – измеряемая величина, а — результат измерений, (читается
«дельта а»)– погрешность измерений.
2.
Формула скорости:
, где
–
скорость (м/с), – путь (м),
–
время(с).
3.
Формула пути и времени: , где
–
скорость(м/с), – путь (м),
–
время (с).
4.
Формула плотности: , где m
– масса (кг), (читается «ро»)–
плотность тела(кг/м3), V
— объём тела (м3).
5.
Формула для определения массы тела и
объёма: , где m
– масса (кг), (читается «ро») –
плотность тела (кг/м3), V
— объём тела (м3).
6.
Сила тяжести: , где m
– масса тела (кг), g – ускорение
свободного падения (м/с2).
7.
Вес тела: ,
где m
– масса тела (кг), g – ускорение
свободного падения (м/с2).
8.
Закон Гука: , где
– сила
упругости (Н), k – жесткость
пружины (Н/м), – удлинение (м).
9.
Равнодействующая двух сил,
направленных в одну сторону: ,
где R
— равнодействующая сила (Н), ,
– силы, действующие на
тело (Н).
10. равнодействующая
двух сил, направленных в разные стороны: , где R
— равнодействующая сила (Н), ,
– силы, действующие на
тело (Н).
11. Формула
для расчета давления: , где p
– давление (Па), F – сила,
действующая перпендикулярно (Н), S
– площадь поверхности (м2).
12. Давление
жидкости или газа на дно сосуда: , где p
– давление (Па), g – ускорение
свободного падения (м/с2), – плотность жидкости или
газа (кг/м3), h – высота столба
жидкости или газа (м).
13. Сила
Архимеда: , где
– сила Архимеда (Н),
– ускорение свободного
падения (м/с2), – плотность жидкости
(кг/м3), – объём, погруженной
части тела (м3).
14. механическая
работа: , где
А – механическая работа (Дж), F
– сила (Н), s – путь (м).
15. Мощность:
, где А – механическая
работа (Дж), – время (с).
16. Момент
сил:
, где F
– сила (Н), – плече силы (м).
17. Коэффициент
полезного действия (КПД): , где
(читается «эта») – КПД
(%), – полезная
работа (Дж), – затраченная
работа (Дж).
18. Потенциальная
энергия: , где
—
потенциальная энергия (Дж), – высота, на которую
поднято тело (м), – ускорение свободного
падения (м/с2), m
– масса тела (кг).
19. Кинетическая
энергия: , где
– кинетическая энергия
(Дж), – скорость (м/с), m
– масса тела (кг).
Копирование и распространение материалов сайта разрешается и очень приветствуется при
наличии ссылки на сайт и автора.
«Если у тебя есть яблоко, и у меня есть яблоко, и мы обменяемся этими яблоками, то у каждого
из
нас так и будет одно яблоко… Если у тебя есть идея, и у меня есть идея, и мы обменяемся
этими идеями,
то у каждого из нас будет по две идеи!«
Бернард Шоу
Массу человека, если известен его вес, можно найти, используя формулу m=Pg, где g≈10Нкг. Масса человека равна 76010 = 76 кг.
Как определить массу тела по его весу?
Получится m = P/g. Подставьте известные значения: m = 549/9,8 = 56 кг. Вы решили задачу. Ответ: масса тела, которое весит 549 Н (на поверхности Земли) равна 56 кг, или m = 56 кг.
Как найти массу тела 7 класс?
Решение: Чтобы найти массу тела, нужно плотность умножить на объем: m = ρ · V. Подставим числовые значения величин: 930 кг/м3 · 0,003 м3 = 2,79 кг.
Как найти массу?
Масса тела выражается через плотность и объем следующей формулой: Масса тела — есть произведение плотности вещества из которого состоит тело на его объем. Здесь: … m — масса тела, (килограмм), ρ — плотность вещества, (кг/м³).
Чему равен вес тела при свободном падении?
Вес, сила, с которой тело, покоящееся в поле сил тяжести, действует на подвес или горизонтальную опору, препятствующую свободному падению тела. Численно В. тела Р равен действующей на него силе тяжести, то есть Р = mg, где m — масса тела, g — ускорение свободного падения (или ускорение силы тяжести).
Как найти массу тела в физике формула?
Масса тела зависит от его объема и плотности вещества, из которого состоит данное тело. — Как найти объем тела, если известна его масса и вещество, из которого состоит тело? Чтобы найти массу тела нежно его плотность умножить на объем. Чтобы найти объем тела, нужно его массу разделить на плотность.
Как узнать массу вещества в растворе?
Масса раствора определяется по формуле m (раствора)= m (масса растворенного вещества)/ w (массовая доля растворенного вещества). Или m = r (плотность раствора — г/см3) * V (объем раствора).
Как найти плотность в физике 7 класс формула?
Плотность равна отношению массы тела к его объёму. В физике плотность обозначают греческой буквой ρ (ро). плотность = масса объём ρ = m V , где m — масса, V — объём. Основной единицей плотности вещества является кг м 3 .
Как найти массу силу тяжести?
Формула силы тяжести Fт=m*g, где m-масса тела, g-ускорение свободного падения. Для тела массой m=400 г =0.4 кг сила тяжести составит Fт=0.4*10=4 Н. Формула силы тяжести: F=mg, где m- масса тела, g-Н/кг.
Что такое масса 7 класс?
Масса тела – это физическая величина, которая является мерой инертности тела. Чем больше масса тела, тем больше его инертность.
Какой прибор измеряет массу?
В Международной системе единиц (СИ) масса измеряется в килограммах. Единицей измерения массы в системе СГС является грамм (1⁄1000 килограмма).
Чему равна масса?
Масса – характеристика, которая определяет интенсивность воздействия на него гравитационного поля. Масса тела (m) равна его плотности (p) умноженной на объём (V). Единица измерения массы – килограмм (кг).
Как найти массу цилиндра?
V = π·r²·h
- через высоту цилиндра и радиус основания;
- через высоту цилиндра и площадь основания.
21.01.2020
Что такое сила тяжести и вес тела?
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
В чем измеряется вес тела в физике?
Вес — сила, с которой тело действует на опору (или подвес, или другой вид крепления), препятствующую падению, возникающая в поле сил тяжести. Единица измерения веса в Международной системе единиц (СИ) — ньютон, иногда используется единица СГС — дина.
Почему в состоянии невесомости вес космонавта равен нулю а сила тяжести нет?
На космонавта действует сила тяжести , где — ускорение свободного падения на высоте h. … То есть сила реакции опоры равна нулю, а значит, по третьему закону Ньютона равен нулю и вес космонавта.
Для того чтобы определить плотность вещества, надо массу тела разделить на его объем:
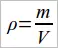
Массу тела можно определить с помощью весов. А как найти объем тела?
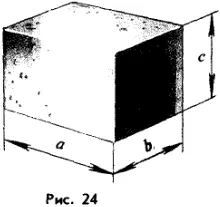
Если тело имеет форму прямоугольного параллелепипеда (рис. 24), то его объем находится по формуле
V = аbс.
Если же у него какая-то другая форма, то его объем можно найти методом, который был открыт древнегреческим ученым Архимедом в III в. до н. э.
Архимед родился в Сиракузах на острове Сицилия. Его отец, астроном Фидий, был родственником Гиерона, ставшего в 270 г. до н. э. царем города, в котором они жили.
До нас дошли не все сочинения Архимеда. О многих его открытиях стало известно благодаря более поздним авторам, в сохранившихся трудах которых описываются его изобретения. Так, например, римский архитектор Витрувий (I в. до н. э.) в одном из своих сочинений рассказал следующую историю:
«Что касается Архимеда, то изо всех его многочисленных и разнообразных открытий то открытие, о котором я расскажу, представляется мне сделанным с безграничным остроумием.
Во время своего царствования в Сиракузах Гиерон после благополучного окончания всех своих мероприятий дал обет пожертвовать в какой-то храм золотую корону бессмертным богам. Он условился с мастером о большой цене за работу и дал ему нужное по весу количество золота. В назначенный день мастер принес свою работу царю, который нашел ее отлично исполненной; после взвешивания вес короны оказался соответствующим выданному весу золота.
После этого был сделан донос, что из короны была взята часть золота и вместо него примешано такое же количество серебра. Гиерон разгневался на то, что его провели, и, не находя способа уличить это воровство, попросил Архимеда хорошенько подумать об этом. Тот, погруженный в думы по этому вопросу, как-то случайно пришел в баню и там, опустившись в ванну, заметил, что из нее вытекает такое количество воды, каков объем его тела, погруженного в ванну. Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)».
Затем, пишет Витрувий, Архимед взял сосуд, доверху наполненный водой, и опустил в него золотой слиток, равный по весу короне. Измерив объем вытесненной воды, он снова наполнил сосуд водой и опустил в него корону. Объем воды, вытесненной короной, оказался больше объема воды, вытесненной золотым слитком. Больший объем короны означал, что в ней присутствует менее плотное, чем золото, вещество. Поэтому опыт, проделанный Архимедом, показал, что часть золота была похищена.
Итак, для определения объема тела, имеющего неправильную форму, достаточно измерить объем воды, вытесняемой данным телом. Располагая измерительным цилиндром (мензуркой), это сделать несложно.
В тех случаях, когда известны масса и плотность тела, его объем можно найти по формуле, вытекающей из формулы (10.1):
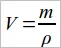
Отсюда видно, что для определения объема тела надо массу этого тела разделить на его плотность.
Если, наоборот, объем тела известен, то, зная, из какого вещества оно состоит, можно найти его массу:
m = ρV. (10.3)
Чтобы определить массу тела, надо плотность тела умножить на его объем.
1. Какие способы определения объема вы знаете? 2. Что вам известно об Архимеде? 3. Как можно найти массу тела по его плотности и объему?
Экспериментальное задание. Возьмите кусок мыла, имеющий форму прямоугольного параллелепипеда, на котором обозначена его масса. Проделав необходимые измерения, определите плотность мыла.
На прошлом уроке мы познакомились с определением плотности тела, узнали формулу, по которой можно ее рассчитать: $rho = frac{m}{V}$.
Сейчас нам предстоит взглянуть на эту формулу с других сторон. Мы научимся находить объем и массу по известной плотности материала тела, решать задачи, используя полученные знания.
Расчет массы тела по его плотности
Знание плотности веществ очень важно для многих практических целей. Для инженеров и строителей, например, знание плотности имеет колоссальное значение — так они могут рассчитать массу будущего механизма или строения.
Как вычисляется масса тела по его плотности и объему?
Плотность определяется по формуле $rho = frac{m}{V}$. Выразим отсюда массу:
$m = rho V$.
Чтобы рассчитать массу тела, если известны его объем и плотность, нужно плотность умножить на объем.
Задача на расчет массы
Рассмотрим пример задачи на расчет массы.
Рассчитайте массу детали, изготовленной из латуни, объемом $0.15 space м^3$.
Из таблицы 1 предыдущего урока берем значение плотности латуни. Она равна $8500 frac{кг}{м^3}$.
Дано:
$rho = 8500 frac{кг}{м^3}$
$V = 0.15 space м^3$
$m -?$
Показать решение и ответ
Скрыть
Решение:
$m = rho cdot V$,
$m = 8500 frac{кг}{м^3} cdot 0.15 space м^3 = 1275 space кг approx 1.3 space т$.
Ответ: $m = 1275 space кг approx 1.3 space т$.
Расчет объема тела по его плотности
По какой формуле можно определить объем тела?
Подобным образом выразим из формулы плотности объем:
$V = frac{m}{rho}$.
Чтобы рассчитать объем тела, если известны его масса и плотность, нужно массу разделить на плотность.
Данной формулой для определения объема часто пользуются в тех случаях, когда тела имеют сложную неправильную форму.
Задача на расчет объема
Рассмотрим пример задачи на расчет объема.
Молоко в бутылке имеет массу $1.03 space кг$. Рассчитайте объем бутылки.
В таблице 2 прошлого параграфа находим молоко: его плотность равна $1030 frac{кг}{м^3}$.
Дано:
$rho = 1030 frac{кг}{м^3}$
$m = 1.03 space кг$
$V -?$
Решение:
$V = frac{m}{rho}$,
$V = frac{1.03 space кг}{1030 frac{кг}{м^3}} = 0.001 space м^3 = 1 space л$.
Ответ: $V = 1 space л$.
Дополнительные задачи
Задача №1
На рисунке 1 изображен кусок хозяйственного мыла в упаковке. По данным производителя размеры размеры его полиэтиленовой упаковки составляют 6 см x 9 см x 5,5 см.
Масса одного куска 200 г. Масса брутто (масса товара вместе с упаковкой) указан 211 г. Найдите объем куска мыла без упаковки. Выразите ответ в СИ.
Обозначим стороны упаковки как $a, b space и space с$, массу куска была $m_м$, массу куска мыла в упаковке — $m$, а общую массу мыла в упаковке — $m_{уп}$.
Объем куска мыла будем обозначать как $V_м$, а вместе с упаковкой — $V$.
Дано:
$a = 6 space см$
$b = 9 space см$
$c = 5.5 space см$
$m_м = 200 space г$
$m = 211 space г$
$V_м -?$
Показать решение и ответ
Срыть
Решение:
Найдем массу упаковки:
$m_{уп} = m — m_м$,
$m_{уп} = 211 space г — 200 space г = 11 space г$.
Общий объем упаковки и мыла:
$V = a cdot b cdot c$,
$V = 6 space см cdot 9 space см cdot 5.5 space см = 297 space см^3$.
Указано, что упаковка изготовлена из полиэтилена (из таблицы 1 предыдущего параграфа его плотность $rho_п$ равна $0.92 frac{г}{см^3}$).
Найдем объем упаковки $V_{уп}$:
$V_{уп} = frac{m_{уп}}{rho_{уп}}$,
$V_{уп} = frac{11 space г}{0.92 frac{г}{см^3}} approx 12 space см^3$.
Общий объем куска мыла в упаковке складывается из объема самого куска и объема упаковки. Так мы можем найти объем куска мыла:
$V_м = V — V_{уп}$,
$V_м = 297 space см^3 — 12 space см^3 = 285 space см^3$.
Выразим в СИ:
$285 space см^3 = 285 cdot 1 space см cdot 1 space см cdot 1 space см = 285 cdot 0.01 space м cdot 0.01 space м cdot 0.01 space м = 285 cdot 0.000001 space м^3 = 0.000285 space м^3$.
Ответ: $V_м = 0.000285 space м^3$
Задача №2
Масса чугунного шара составляет 800 г. Его объем — $125 space см^3$. Будет ли этот шар сплошным (отлитым полностью из одного материала) или полым (иметь пространство внутри, заполненное, например, воздухом)?
Показать решение
Скрыть
Проверить это достаточно просто: рассчитаем плотность этого шара:
$rho = frac{m}{V}$,
$rho = frac{800 г}{125 space см^3} = 6.4 frac{г}{см^3}$.
Сравним полученное значение с табличной плотностью чугуна:
$rho = 7 frac{г}{см^3}$
Сколько бы тогда весил сплошной шар?
$m = rho V$,
$m = 7 frac{г}{см^3} cdot 125 space см^3 = 875 space г$.
Разница между массами реального и предполагаемого сплошного шара составляет 75 г.
Следовательно, реальный шар имеет внутри какую-то полость, он не полностью выполнен из чугуна.
Задача №3
В грузовой автомобиль загрузили 48 сосновых бревен. Масса каждого соснового бревна составляет $20 space дм^3$. На сколько увеличилась масса автомобиля после загрузки?
Из таблицы 1 предыдущего параграфа возьмем плотность сухой сосны ($400 frac{кг}{м^3}$). Переведем $20 space дм^3$ в $м^3$:
$20 space дм^3 = 20 cdot 0.1 space м cdot 0.1 space м cdot 0.1 space м = 20 cdot 0.001 space м^3 = 0.02 space м^3$.
Количество брусков — $n$.
Дано:
$V = 20 space дм^3$
$rho = 400 frac{кг}{м^3}$
$n = 48$
СИ:
$V = 0.02 space м^3$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем массу одного соснового бревна:
$m = rho cdot V$,
$m = 400 frac{кг}{м^3} cdot 0.02 space м^3 = 8 space кг$.
Масса всех сосновых бревен (M) будет равна:
$M = n cdot m$,
$M = 48 cdot 8 space кг = 384 space кг$
Ответ: масса автомобиля после загрузки увеличится на 384 кг.
Упражнения
Упражнение №1
Какова масса $0.5 space л$ спирта, молока, ртути?
Дано:
$V = 0.5 space л$
$rho_1 = 800 frac{кг}{м^3}$
$rho_2 = 1030 frac{кг}{м^3}$
$rho_3 = 13600 frac{кг}{м^3}$
СИ:
$V = 5 cdot 10^{-4} space м^3$
$m_1 — ?$
$m_2 — ?$
$m_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Зная объем и плотность тела, мы может рассчитать его массу по формуле: $m = rho V$.
Рассчитаем массу спирта:
$m_1 = rho_1 V$,
$m_1 = 800 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 0.4 space кг$.
Рассчитаем массу молока:
$m_2 = rho_2 V$,
$m_2 = 1030 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 0.515 space кг$.
Рассчитаем массу ртути:
$m_3 = rho_3 V$,
$m_3 = 13600 frac{кг}{м^3} cdot 5 cdot 10^{-4} space м^3 = 6.8 space кг$.
Ответ: $m_1 = 0.4 space кг$, $m_2 = 0.515 space кг$, $m_3 = 6.8 space кг$.
Упражнение №2
Определите объем льдинки, масса которой $108 space г$.
Дано:
$m = 108 space г$
$rho = 900 frac{кг}{м^3}$
СИ:
$m = 0.108 space кг$
$V — ?$
Показать решение и ответ
Скрыть
Решение:
Зная массу и плотность льда, рассчитаем его объем:
$V = frac{m}{rho}$,
$V = frac{0.108 space кг}{900 frac{кг}{м^3}} = 0.00012 space м^3 = 120 space см^3$.
Ответ: $V = 120 space см^3$.
Упражнение №3
Сколько килограммов керосина входит в пятилитровую бутыль?
Дано:
$V = 5 space л$
$rho = 800 frac{кг}{м^3}$
СИ:
$V = 5 cdot 10^{-3} space м^3$
$m — ?$
Показать решение и ответ
Скрыть
Решение:
Зная плотность и объем, найдем массу керосина:
$m = rho V$,
$m = 800 frac{кг}{м^3} cdot 5 cdot 10^{-3} space м^3 = 4 space кг$.
Ответ: $m = 4 space кг$.
Упражнение №4
Грузоподъемность лифта составляет $3 space т$. Сколько листов железа можно погрузить в лифт, если длина каждого листа равна $3 space м$, ширина — $60 space см$ и толщина — $4 space мм$?
Дано:
$M = 3 space т$
$a = 60 space см$
$b = 4 space мм$
$c = 3 space м$
$rho = 7800 frac{кг}{м^3}$
СИ:
$M = 3000 space кг$
$a = 0.6 space м$
$b = 0.004 space м$
$n — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем массу одного железного листа. Для этого нам нужно знать его объем (плотность мы взяли из таблицы). Объем мы может вычислить, перемножив друг на друга ширину, высоту и длину: $V = a cdot b cdot c$.
Масса железного листа:
$m = rho V = rho cdot a cdot b cdot c$,
$m = 7800 frac{кг}{м^3} cdot 0.6 space м cdot 0.004 space м cdot 3 space м = 56.16 space кг$.
Теперь разделим грузоподъемность лифта на массу одного лифта. Полученное целое число и будет ответом на вопрос задачи:
$n = frac{M}{m}$,
$n = frac{3000 space кг}{56.16 space кг} approx 53$.
Ответ: $n = 53$.
Упражнение №5
Кружка доверху наполнена молоком. Определите объем кружки, если масса молока в кружке $515 space г$, плотность молока найдите в таблице.
Дано:
$m = 515 space г$
$rho = 1030 frac{кг}{м^3}$
СИ:
$m = 0.515 space кг$
$V — ?$
Показать решение и ответ
Скрыть
Решение:
Зная массу и плотность молока, найдем объем, который оно занимает в кружке:
$V = frac{m}{rho}$,
$V = frac{0.515 space кг}{1030 frac{кг}{м^3}} = 0.0005 space м^3 = 0.5 space л$.
Ответ: $V = 0.5 space л$.
Задание
Возьмите баночку из-под меда. Рассмотрите внимательно этикетку. Найдите на ней, какова масса меда и объем баночки. Затем рассчитайте плотность меда. Полученный результат проверьте по таблице.
Дано:
$m = 800 space г$
$V = 500 space мл$
СИ:
$m = 0.8 space кг$
$V = 0.0005 space м^3$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Рассчитаем плотность меда:
$rho = frac{m}{V}$,
$rho = frac{0.8 space кг}{0.0005 space м^3} = 1600 frac{кг}{м^3}$.
По таблице плотность меда составляет $1350 frac{кг}{м^3}$. Существует множество различных сортов меда, плотность которых отличается друг от друга. Наше значение плотности не сильно отличается от табличного, поэтому можно сказать, что результат получен правильный.
Ответ: $rho = 1600 frac{кг}{м^3}$.