2.6. Физические приложения тройного интеграла
Сначала разомнёмся физически (давно пора), тело – в дело :). Пожалуйста, встаньте и найдите какой-нибудь пакет или мешок.
Можно коробку. Теперь походите по квартире, ну или по улице и наведём порядок. А именно, наполним тару мусором.
…Очень хорошо, молодцы! В результате ваших трудов получено ограниченное тело неоднородной плотности. Как
говорится, есть бумажка, а есть жестяная крышка. Воздух, кстати, тоже обладает вполне определённой плотностью. Напоминаю, что
физическая плотность – есть отношение единицы массы к единице объёма, например, 100 грамм на
кубический метр (средняя плотность хлопка) или 19,32 грамма на кубический сантиметр (да, всего лишь на сантиметр – это
плотность чистого золота).
Ставим мешок рядышком и читаем дальше:
2.6.1. Масса тела
Рассмотрим неоднородное (переменной плотности) тело . Если известна непрерывная в области
функция
плотности тела, то его масса равна следующему тройному интегралу:
Возможно, не всем до конца понятен смысл функции плотности. Поясняю: если взять произвольную точку , принадлежащую телу
, то значение функции
будет равно плотности тела в данной точке. В частности, если эта функция равна
константе: , то речь идёт об однородном
теле («мешок» хлопка или золота, например).
Но на практике не всё так легко:
Пример 50
Вычислить массу неоднородного тела, ограниченного поверхностями , если известна функция его плотности
.
Решение: искомое тело ограничено цилиндром сбоку, эллиптическим параболоидом
– сверху и плоскостью
– снизу. Дополнительные условия
«загоняют нас» в 1-й октант, и проекция тела на плоскость
представляет собой соответствующую «четвертинку»
единичного круга:
Аналитическим методом уточним высоту, на которой параболоид пересекает цилиндр: 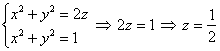
Проекция тела на плоскость сразу же наводит
на мысль о переходе к цилиндрической системе координат . Найдём уравнения поверхностей в этой системе:
– цилиндр;
– и параболоид.
Порядок обхода тела очевиден:
(не забываем, что у нас только
«четвертинка» круга!)
Осталось преобразовать подынтегральную функцию:
и осуществить переход:
Вычисления элементарны:
Ответ: ед. массы, то
есть, в предложенном теле (см. чертёж выше) содержится одна единица (грамм, килограмм или другая) массы.
Пример 51
Вычислить массу неоднородного тела, ограниченного поверхностями , если известна функция его плотности
.
Краткое решение в конце книги. И старая песня о главном:


| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
ЗАМЕЧАНИЕ.
При решении следующих задач будут
использованы термины, которые мы сейчас
введем.
Область
(D)
плоскости
будем
называть y—трапецией,
если она может быть задана системой
неравенств вида a
x
b,
y1(x)
y
y2(x).
Такая
область допускает удобную штриховку
вертикальными отрезками: все их нижние
концы лежат на кривой y
= y1(x),
все верхние на
кривой y
y2(x)
(рис.71).
Аналогично
введем понятие x—трапеции:
c
y
d,
x1(y)
x
x2(y).
(рис.71).
Для
x-трапеции
удобна горизонтальная штриховка.
Рис.71
В
случае y-трапеции
=

в
случае x-трапеции
=
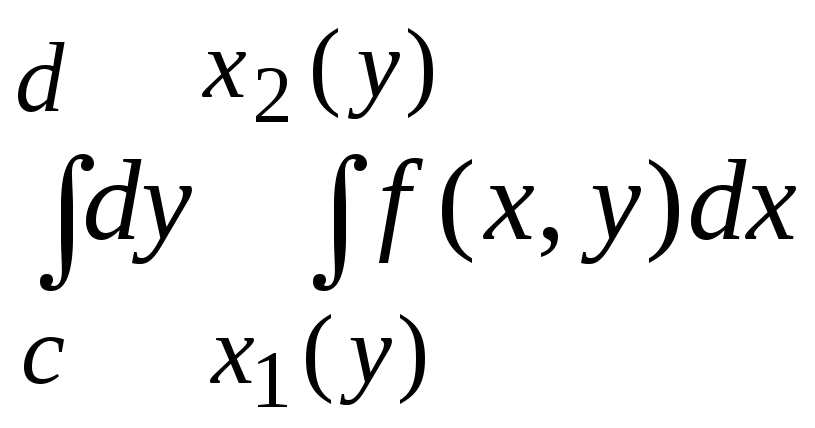
Тело
(T)
в пространстве
назовем z—брусом,
если оно может быть задано следующим
образом: (x,
y)D
длянекоторой
области D
в плоскости
,
ограниченной замкнутой кусочно-гладкой
кривой, z1(x,y)
z
z2(x,y).
Каждый z-брус
может быть “заполнен” отрезками
,параллельными оси
,
нижние концы которых лежат на поверхности
z
z1(x,y)
”дне”,
а верхние
на поверхности z
z2(x,y)
”крышке”.
Аналогично введем понятия y—бруса
и x—бруса
(рис.72).
В
случае z-бруса

Рис.72
ЗАДАНИЕ
5. Изменить
порядок интегрирования в интеграле
.
РЕШЕНИЕ.
Восстановим
область интегрирования ()
по пределам повторных интегралов:
=
1
2,
(1):
;
(2):
Изобразим
область интегрирования на чертеже.
Найдем точки пересечения параболы
и прямой
:
т.е. точкам пересечения кривых соответствуют
точки, для которых
и
.
Вертикальной штриховкой покажем порядок
интегрирования: сначала по
y
при фиксированном x.
Сменим
штриховку на горизонтальную. Из рисунка
видно, что данная область является
-трапецией.
Рис.73
Уравнение
“нижней” кривой есть
,
“верхней” — прямая
.
Поэтому ():
и в
результате подстановки пределов получим
следующий повторный интеграл:
Ответ.
ЗАДАНИЕ
6.
Найти объем
тела, ограниченного поверхностями
;
.
РЕШЕНИЕ.
Тело
ограничено с “боков” плоскостью
и цилиндром (цилиндрической поверхностью)
.
“Снизу” тело “накрыто” плоскостью
,
сверху – плоскостью
.
Изобразим на чертеже заданное тело
(рис.74).
Рис.74
Очевидно,
тело
есть
—
цилиндрический брус. Область (),
являющуюся ортогональной проекцией
тела
на плоскость
,
изобразим на отдельном рисунке. Для
этого найдем точки пересечения параболы
с прямой
.
Опуская подробности вычислений, получим,
что прямая и “положительная” ветвь
параболы пересекаются в точке, в которой
.
Объем цилиндрического бруса может
быть найден с помощью двойного интеграла.
Учитывая, что тело “стоит” на плоскости
,
для объема запишем формулу
и перейдем к повторному интегралу.
Область (),
изображенная на рисунке, очевидно не
является
—
трапецией, но является
—
трапецией:
():
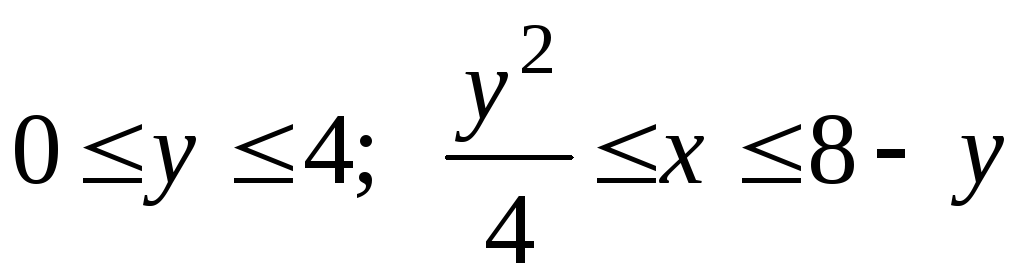
Записав объем через
повторный интеграл и производя вычисления,
последовательно получим
V=
Ответ.
Объем тела равен 80.
ЗАДАНИЕ
7.
Найти объем
тела, ограниченного указанными
поверхностями.
Приведем
решение двух задач на вычисление объемов
тел, рассматривая тела с различной
геометрией поверхности.
1)

2)
.
РЕШЕНИЕ.
1).
Тело
ограничено двумя поверхностями:
параболоидом
и плоскостью
.
Изобразим это тело на чертеже (рис.75).
Рис.75
Данное
тело является
-цилиндрическим
брусом (рис.72); боковая поверхность
выродилась в линию пересечения заданных
поверхностей. Найдем область, в которую
тело проектируется на плоскость
,
для чего из уравнений поверхностей,
ограничивающих тело, следует исключить
переменную
(т.е. совершить ортогональное
проектирование):
и
.
Таким
образом, областью ()
является круг с центром в точке (0; 1)
радиуса
=1
(см. рис.75).
Объем
тела может быть вычислен с помощью
тройного интеграла по формуле
.
В декартовой системе координат тройной
интеграл записывается через повторный
следующим образом:

откуда
видно, что его вычисление сопряжено со
значительными трудностями (на завершающей
стадии вычисления повторного интеграла).
Запишем
интеграл в цилиндрической системе
координат
,
с которой
декартова система связана формулами
.
Якобиан
преобразования
.
Формула перехода (в интеграле) имеет
вид
.
В
нашем случае
.
Запишем
уравнения параболоида и плоскости в
цилиндрической системе координат:
;
.
Для
окружности
имеем
;
угол
,
очевидно, необходимо менять в пределах
от 0 до
.
Таким образом ,

==
=
.
Ответ.
=
.
2)
Изобразим тело
,
ограниченное поверхностями цилиндра
,
параболоида
и плоскостью
(рис.76).
Рис.76
Замечание.
При построении следует преобразовать
уравнение направляющей цилиндра
,
лежащей в плоскости
к каноническому виду (прибавляя и
вычитая 2):
,
откуда получим
,
то есть направляющей цилиндра в плоскости
служит окружность с центром в точке
радиуса
.
Кроме того, при построении следует
учесть, что поверхность параболоида
пересекается с плоскостью
по окружности
.
Тело
является z-цилиндрическим брусом,
проектирующимся на плоскость
в область (),
являющуюся
-трапецией.
Нетрудно
убедиться, что и здесь, как и в предыдущем
случае, повторный интеграл, записанный
в декартовой системе координат, при
вычислении требует значительных усилий;
поэтому и в этом случае перейдем к
цилиндрической системе координат (см.
предыдущую задачу):
.
Найдем
уравнения поверхностей, ограничивающих
тело, в цилиндрической системе координат:
уравнение цилиндра
перейдет в
,
уравнение параболоида
– в
,
плоскости
– в
.
Область (),
являющаяся проекцией тела на плоскость
,
ограничена окружностью
и окружностью
(так как
).
Найдем значения параметра
,
соответствующие точкам пересечения
этих окружностей:
,
откуда
и для
получим два значения:
.
Учитывая симметрию тела
относительно плоскости
,
объем
запишем в виде следующего повторного
интеграла:

Приведем
вычисление объема:
=
=
=
Ответ.
.
ЗАДАНИЕ
8.
Найти объем тела
,
ограниченного поверхностями
а)
;
б)
;
в)
.
РЕШЕНИЕ.
Изобразим
тело, ограниченное двумя концентрическими
сферами с центрами в начале координат
и радиусами 8 и 12 и (“снизу”)
конусом
;
от полученного таким образом тела
плоскостями
и
“отрезается” заданное условием задачи
тело (V) (рис.77) .
Рис.77
Объем
тела может быть вычислен по формуле
.
Рассматривая тело в декартовой системе
координат, видим, что оно не является
ни
-,
ни
-,
ни
-цилиндрическими
брусами (см. рис.72); разбиение тела на
z—
цилиндрические бруски является само
по себе не простой задачей, не говоря
уже о вычислении повторных интегралов.
“Конструкция” тела
такова, что вычисление тройного интеграла
удобнее провести в сферической системе
координат r,,
связанной с декартовой системой
координат формулами:
;
;
.
Якобиан
такого преобразования
.
Для объема получим:
.
Чтобы тройной интеграл
записать в виде повторного, перейдем в
уравнениях ограничивающих тело
поверхностей к сферическим координатам.
Следует использовать соотношения
.
Уравнение
переходит в
,
уравнение
в
;
для уравнения конуса
получим последовательно:
,
и
,
откуда
и
;
уравнение плоскости
переходит в уравнение
,
уравнение плоскости
в
,
т.е. в
.
Таким образом,

Так
как подынтегральная функция представляет
собой произведение функций, каждая из
которых зависит только от одной
переменной, а пределы интегрирования
постоянны, то повторный интеграл
представляет собой просто произведение
трех интегралов

==
;
.
Для
объема тела получим
.
Ответ.
.
ЗАДАНИЕ
9.
Найти массу
пластинки
():
,
Плотность
массы пластинки
|
РЕШЕНИЕ. Область
Подставляя
|
|
Очевидно,
что область ()
не является ни
-,
ни
—
трапецией; при вычислении двойного
интеграла в декартовой системе координат
область ()
пришлось бы разбить на три области. Как
для областей, заключенных между
концентрическими окружностями с центром
в начале координат “родной” является
полярная система координат, так и для
эллиптических колец “своей “ является
эллиптическая система координат
(обобщенная полярная система координат)
;
.
Выбор
обусловлен соображениями удобства при
вычислении интегралов. Положим для
заданной области
:
;
.
Якобиан
преобразования вычисляется по формуле
.
Совершим
преобразование области ():
уравнение эллипса
перейдет в
,
т.е.
эллипс преобразуется в
окружность
радиуса 1; эллипс
переходит в окружность
;
прямая
в луч
,
прямая
в луч
(действительно,
и
).
Запишем двойной интеграл в обобщенной
полярной системе координат:
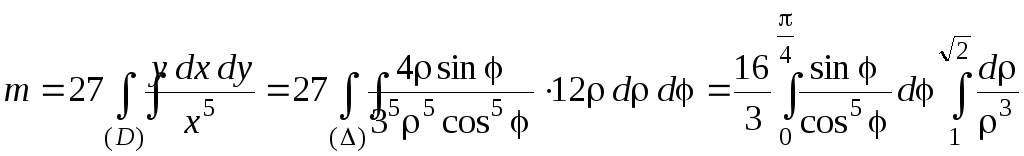
В
данном случае повторный интеграл есть
произведение двух определенных
интегралов, так как внутренний интеграл
по
есть скаляр. Вычислим их:
;
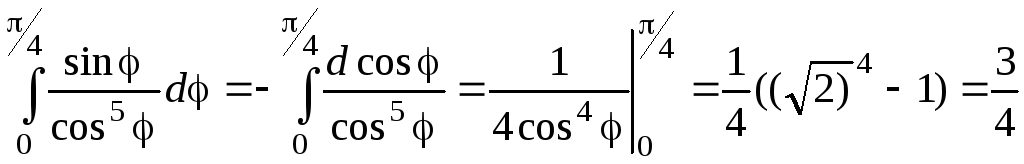
Таким
образом,
.
Ответ.
Масса пластинки равна 1.
ЗАДАНИЕ
10. Найти
массу тела
,
ограниченного
поверхностями:
;
;
;
;
плотность массы тела
.
РЕШЕНИЕ.
Область
ограничена с боков координатными
плоскостями
и цилиндрической поверхностью
.
Снизу она “накрыта” плоскостью
,
сверху
поверхностью параболоида
(рис.79).
Рис.79
Область
является
-цилиндрическим
брусом. Масса тела может быть вычислена
по формуле:
.
Цилиндрический
брус проектируется на плоскость
в криволинейную трапецию (D):
0
x
1,
0
y
.
Преобразуем
тройной интеграл в повторный и вычислим
его:
=
=[
замена переменных
;
;
;
]=
(схема 41)
Для функции трех переменных имеет место обобщение определенного интеграла — тройной интеграл (также кратный интеграл). Его теория аналогична теории двойного интеграла.
Пусть непрерывная функция u=f (x,y,z) задана в
некоторой ограниченной замкнутой пространственной области V (рис. 6.4). Разобьем эту область на пространственные
ячейки 
В каждой ячейке 
точку 
функции f в этой точке на объем ∆νi ячейки Vi. Сумма таких произведений по всем ячейкам
интегральной
суммой. Обозначим через d(Vi) диаметр ячейки Vi, то есть расстояние между наиболее удаленными точками
этой ячейки, и max d(Vi)
– наибольший из диаметров всех ячеек данного разбиения.
Тройным интегралом 
то есть при неограниченном увеличении числа ячеек, когда все ячейки стягиваются
в точку:

Если такой предел существует, то функция f(M)
называется интегрируемой в области V; всякая непрерывная в ограниченной замкнутой области V функция f(M)
интегрируема в ней. В дальнейшем мы будем рассматривать только непрерывные
функции.
В декартовых координатах элемент объема обычно
записывают в виде dν=dxdydz, а
тройной интеграл обозначают

Тройной интеграл (6.9) выражает массу неоднородного тела объема V, с плотностью в каждой точке γ=f (x,y,z) посредством формулы:

Координаты
центра тяжести тела
вычисляются по формулам:

Если плотность γ=1,
то тройной интеграл (6.9) будет выражать собой объем области V, а формулы
(6.11) будут представлять координаты центра тяжести однородного тела.
1.
Вычисление тройного интеграла в декартовой системе координат
Пусть V проектируется в область D на плоскости x0y так, что всякая прямая, параллельная оси 0z и
проходящая внутри области D, пересекает границу области V ровно в
двух точках. В общем случае такая область ограничена сверху поверхностью z=ψ2(x,y), снизу –
поверхностью z=ψ1(x,y) и с боков – цилиндрической поверхностью с
образующими, параллельными оси 0z (рис. 52). Такая область V называется правильной. В частных случаях
боковая поверхность цилиндра может превратиться в линию. Функции ψ1(x,y) и ψ2(x,y) мы будем считать непрерывными. Тройной интеграл по
такой области вычисляется по формуле

Здесь
внутренний интеграл 
произвольных в D значениях x и y, от нижней границы области V до ее
верхней границы, то есть по отрезку KL (рис. 6.4). В
результате получается некоторая функция двух переменных x и y, которая
интегрируется затем по области D с помощью формул (6.5) или (6.6). Таким образом,
вычисление тройного интеграла сводится к трехкратному интегрированию.
Наиболее простой вид формула (6.12) принимает в
случае, когда V есть прямоугольный параллелепипед, ограниченный
плоскостями 

Если область V имеет более сложную форму, то ее разбивают на
конечное число областей 
Примечание. Аналогичные определения и формулы могут быть
получены и тогда, когда область V проектируется в область D, лежащую или в плоскости x0z, или в плоскости
y0z
Пример 6.4. Вычислить тройной интеграл 
Решение. Область V – треугольная пирамида – ограничена снизу плоскостью z=0, сверху –
плоскостью z=1–x–y. Область V проектируется на плоскость x0y в виде
прямоугольного треугольника, который определяется неравенствами 
Пример 6.5. Найти объём тела ограниченного параболоидом z=x2+y2+2 и
плоскостями z=1, x=0, y=0, x+y=2 (рис. 6.6).
Решение. По условию область V задана
неравенствами:

Следовательно,
(единиц
объема)
Пример 6.6. Найти массу тела ограниченного координатными
плоскостями и плоскостью x+y+z=1, если плотность в каждой его точке равна
произведению координат этой точки, то есть γ = f(x,y,z) = x y z.
Решение. По условию область V совпадает с той областью, которая была рассмотрена в
примере 6.4 (см. рис. 6.5). Искомая масса M согласно
формуле (6.11) равна интегралу 

Чтобы
вычислить полученный интеграл, положим 1–x=t; тогда dx= – dt; при этом t=1 при x=0 и t=0 при x=1.
(единиц массы)
Пример 6.7. Вычислить координаты центра тяжести куба 
координат этой точки.
Решение. По условию плотность γ=x y z. Вычислим массу M куба по (6.10):

Из соображений симметрии следует xc = yc = zc. Поэтому достаточно найти только одну координату xc.
Вычислим числитель для xc в формуле (6.11).
2. Вычисление
тройного интеграла в цилиндрических координатах
Для упрощения вычисления тройного интеграла часто
бывает целесообразным перейти к цилиндрическим координатам. Точка M(x;y;z) в
пространстве 0xyz может быть определена заданием трех величин r; φ; z, где
r – длина
радиус-вектора проекции точки M на плоскость x0y, φ – угол, образованный этим радиус-вектором с осью 0x, z –
аппликата точки M (рис. 6.7). Эти
числа (r; φ; z) называются цилиндрическими координатами точки M. Эти
координаты связаны с ее декартовыми координатами соотношениями:



интеграл вычисляется по формуле

После применения (6.15)
вычисление тройного интеграла сводится к
трехкратному по r, по φ и по z
согласно формуле (6.12).
Пример
6.8. Вычислить 

Решение. Заданная область V – часть конуса, вершина которого расположена в начале
координат. Его уравнение в цилиндрических координатах (6.14) имеет вид

как r=2. Новые переменные изменяются в следующих пределах:

оси 0z, пересекающая область D, входит в конус z=r и выходит
из него на высоте z=2).
С учетом формулы замены (6.15) можем вычислить
заданный тройной интеграл:
Обратим внимание на то, что, не переходя к
цилиндрическим координатам, мы получили бы достаточно сложное трехкратное
интегрирование согласно формуле (6.12)
Примечание. Переход
к цилиндрическим координатам рационален, когда область интегрирования
образована цилиндрической или конической поверхностью
3.
Вычисление тройного интеграла в сферических
координатах
Если область интегрирования V представляет собой шар или
его часть (граница шара x2+y2+z2=R2 в сферических координатах имеет очень простой вид ρ=R), то удобно переходить к сферическим
координатам.
Сферическими координатами точки M(x;y;z) пространства 0xyz называется тройка чисел ρ; φ; θ (рис.
6.8), где ρ – длина радиус-вектора точки
M, φ – угол, образованный проекцией радиус-вектора

точки M соотношениями:

В этом случае тройной
интеграл вычисляется по формуле

Примечание. Переход к
сферическим координатам целесообразен также в том случае, когда подынтегральная
функция имеет вид f(x2+y2+z2)
Приложения кратных интегралов в механике
Краткая теория
Масса и статистические моменты пластики
Если
– область плоскости
, занятая пластинкой, и
– поверхностная плотность пластики в точке
, то масса
пластинки и ее статистические моменты
и
относительно осей
и
выражаются двойными интегралами:
Если
пластика однородна, то
Координаты центра тяжести пластики
Если
– центр тяжести пластики, то
где
– масса пластинки и
– ее статистические моменты относительно осей
координат.
Моменты инерции пластики
Моменты
инерции пластинки относительно осей
и
соответственно равны:
Момент инерции пластики относительно
начала координат:
Полагая
, получаем геометрические моменты инерции плоской
фигуры.
Масса тела, занимающего область
![]() и статистические моменты тела относительно
и статистические моменты тела относительно
координатных плоскостей
где
– плоскость тела в точке
Координаты центра тяжести
Если тело
однородно, то формулах для координат центра тяжести можно положить
.
Моменты инерции относительно
осей координат
Полагая в
этих формулах
, получаем геометрические
моменты инерции тела.
Примеры решения задач
Задача 1
Вычислить
массу материальной пластины, занимающей область
плоскости
, если поверхностная
плотность
и границы области
заданы уравнениями.
Решение
Сделаем
чертеж области
:
Искомая
масса материальной пластины:
Ответ:
Задача 2
Найти
статистический момент фигуры, ограниченной линиями
и
относительно оси абсцисс.
Решение
Сделаем
чертеж:
Статистический
момент относительно оси
:
Ответ:
Задача 3
Вычислить
координаты центра масс однородной
материальной пластины
, ограниченной данными
линиями:
Решение
Сделаем
чертеж:
Масса
пластинки:
Статистические
моменты:
Искомые
координаты центра масс:
Ответ:
.
Задача 4
Вычислить массу тела
, ограниченного заданными поверхностями
-плотность в
точке
.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Изобразим
тело на рисунке:
С боков
тело будет ограничено цилиндром
и плоскостями
. Сверху плоскостью
Проекция на плоскость
:
Ответ:
Задача 5
Найти
момент инерции однородного шара
с массой
относительно оси
.
Решение
Момент
инерции относительно оси
можно найти по формуле:
Шар
однородный, поэтому плотность:
Перейдем
к сферическим координатам:
Получаем:
Ответ:

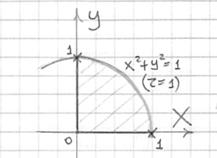
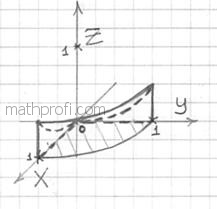
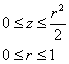
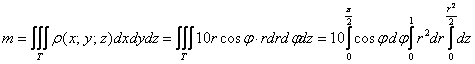

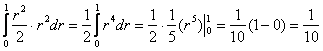
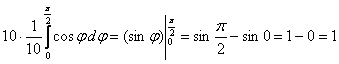











 Рис.78
Рис.78










