На прошлом уроке мы доказали с помощью опытов существование силы, действующей на тела, погруженные в жидкость или газ — выталкивающей силы. Также мы теперь знаем, что ее можно рассчитать по формуле: $F_{выт} = gm_ж = P_ж$. Но какое еще есть значение у этой силы? На этом уроке мы более подробно рассмотрим выталкивающую силу.
Выталкивающая сила и вес тела
Как можно на опыте определить, с какой силой тело, погруженное целиком в жидкость, выталкивается из жидкости?
Давайте познакомимся с таким опытом. Он представлен на рисунке 1.
Подвесим на пружину небольшую емкость для жидкости и тело цилиндрической формы ниже. На конце пружины у нас расположена стрелка-указатель. Она отмечает растяжение пружины на штативе (рисунок 1, а). Таким образом, мы видим вес тела в воздухе.
Теперь опустим наше тело в большой сосуд. Сосуд имеет трубку для слива и наполнен жидкостью до уровня этой трубки (рисунок 1, б).
Когда мы полностью опустим тело в сосуд, часть жидкости из него выльется через трубку для слива в стакан. Объем этой жидкости будет равен объему тела. Мы уже знаем, что на тело действует выталкивающая сила: пружина сокращается, стрелка-указатель поднимается, вес тела в жидкости становится меньше.
А теперь возьмем жидкость, которая вылилась в стакан. Зальем ее в емкость, которая также подвешена к пружине (рисунок 1, в). Теперь стрелка-указатель вернулась к своему изначальному положению.
Так чему равна эта сила? Сделаем вывод из данного опыта.
Сила, выталкивающая целиком погруженное в жидкость тело, равна весу жидкости в объеме этого тела.
Если провести подобный опыт с газом, а не с жидкостью, то мы получим, что сила, выталкивающая тело из газа, равна весу газа, взятого в объеме тела.
Сила Архимеда
Как называют силу, которая выталкивает тела, погруженные в жидкости и газы?
Теперь мы добавим, что эту выталкивающую силу называют архимедовой силой. Архимед (рисунок 2) — древнегреческий ученый и инженер, сделавший множество открытий и в математике, и в физике. Именно он первый обнаружил наличие выталкивающей силы и рассчитал ее значение.
Как подсчитать архимедову силу?
В прошлом уроке мы получили формулу $F_{выт} = P_ж = g m_ж$. Теперь мы будем называть эту силу архимедовой $F_A$.
Из выше рассмотренных опытов мы можем выразить массу вытесненной жидкости через ее плотность и объем тела, который эту жидкость вытеснил (они одинаковы): $m_ж = rho_ж cdot V_т$. Получим формулу для архимедовой силы.
$F_A = g rho_ж V_т$.
От чего зависит архимедова сила?
Взгляните еще раз на формулу: $F_A = g rho_ж V_т$.
Ясно видно, что архимедова сила зависит только от плотности жидкости и от объема тела, которое мы погружаем в эту жидкость.
Если мы будем погружать в одну и ту же жидкость тела разной плотности и разной формы (рисунок 3), то значение силы меняться не будет (при условии, что эти тела будут обладать одинаковым объемом).
Определение веса тела, погруженного в жидкость или газ
На тело, погруженное в жидкость (или в газ), действуют две силы: сила тяжести и архимедова сила. Направлены они в противоположные стороны. Вес тела в жидкости $P_1$ будет меньше веса тела в вакууме $P$ на архимедову силу $F_A$. То есть:
$P_1 = P space − space F_A = gm space − space gm_ж$.
Если тело погружено в жидкость или газ, то его вес уменьшается на вес вытесненной им жидкости или газа.
Пример задачи
Определите выталкивающую силу, которая будет действовать на камень объемом $2.6 space м^3$, лежащий на морском дне.
Дано:
$V_т = 2.6 space м^3$
$rho_ж = 1030 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$F_A — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Сила Архимеда рассчитывается по формуле:
$F_A = g rho_ж V_т$.
Подставим численные значения величин и рассчитаем эту силу:
$F_A = 9.8 frac {Н}{кг} cdot 1030 frac{кг}{ м^3} cdot 2.6 space м^3 approx 26 244 space Н approx 26.2 space кН$.
Ответ: $F_A approx 26,2 space кН$.
Забавное дополнение: легенда об Архимеде
Архимед, великий изобретатель, шокировал своих современников гениальными открытиями. Его имя упоминается во множестве легенд, но одна из них стала наиболее известной: легенда о том, как Архимед пришел к открытию выталкивающей силы.
Царь Гиерон поручил Архимеду проверить работу мастера, который изготовил для него золотую корону.
Долгое время ученый не мог найти ответ: как определить количество некачественных примесей? Проблема заключалась в том, что определить ее объем — сложная задача. По легенде озарение настигло Архимеда, когда он принимал ванну.
Ученый заметил, что из ванны вылилась вода, когда он залез в нее. И здесь его посетила гениальная мысль. Все вы слышали его известную цитату: «Эврика! Эврика!» (в переводе означает: «Нашел! Нашел!»).
Так Архимед победно выкрикивал свою фразу, потрясенный своим открытием, что она дошла в виде легенды и до наших времен.
Упражнения
Упражнение №1
К коромыслу весов подвешены два цилиндра одинаковой массы: свинцовый и алюминиевый (рисунок 4). Весы находятся в равновесии. Нарушится ли равновесие весов, если оба цилиндра одновременно погрузить в воду; в спирт? Ответ обоснуйте. Проверьте его на опыте. Как зависит выталкивающая сила от объема тела?
Посмотреть ответ
Скрыть
Ответ:
Когда мы погрузим цилиндры в жидкость, на каждый их них будет действовать сила Архимеда. Если эти силы будут равны, то весы останутся в равновесии.
Запишем формулы архимедовой силы для каждого цилиндра.
Для свинцового цилиндра:
$F_{A1} = g rho_ж V_1$.
Для алюминиевого цилиндра:
$F_{A2} = g rho_ж V_2$.
Мы видим, что равенство этих сил зависит от объемов цилиндров. Они равны? Нет, они имеют одинаковые массы, но разные плотности. Цилиндр из алюминия будет обладать большим объемом, чем свинцовый цилиндр ($V = frac{m}{rho}$). Значит, на алюминиевый цилиндр будет действовать большая выталкивающая сила, чем на свинцовый.
Если мы проверим это на опыте, то увидим подтверждение нашим выводам (рисунок 5).
При этом весы выйдут из равновесия в случае и с водой (рисунок 5, а), и со спиртом (рисунок 5, б). Так как мы опускаем цилиндры одновременно в один и тот же тип жидкости, значение архимедовой силы, действующей на цилиндры, будет различаться только в зависимости от объемов этих цилиндров — свинцовый перевесит алюминиевый в любой жидкости.
Заметим, что в случае погружения в воду, архимедова сила будет больше, чем в случае погружения в спирт. Это объясняется тем, что вода имеет большую плотность, чем спирт.
Упражнение №2
К коромыслу весов подвешены два алюминиевых цилиндра одинакового объема. Нарушится ли равновесие весов, если один цилиндр погрузить в воду, а другой — в спирт? Ответ обоснуйте. Зависит ли выталкивающая сила от плотности жидкости?
Посмотреть ответ
Скрыть
Ответ:
Если один цилиндр погрузить в воду, а другой — в спирт, то равновесие весов нарушится (рисунок 6). На цилиндр, находящийся в воде, будет действовать большая архимедова сила.
Так происходит, потому что архимедова сила зависит от объема погруженного тела (а они у нас одинаковые: $V_1 = V_2 = V$) и от плотности жидкости:
$F_А = g rho_ж V$.
Плотность спирта ($800 frac{кг}{м^3}$) меньше плотности воды ($1000 frac{кг}{м^3}$). Значит, на цилиндр, погруженный в воду, будет действовать большая архимедова сила, чем на тот, что погружен в спирт.
Упражнение №3
Объем куска железа равен $0.1 space дм^3$. Какая выталкивающая сила будет на него действовать при полном его погружении в воду; в керосин?
Дано:
$V = 0.1 space дм^3$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 800 frac{кг}{м^3}$
СИ:
$V = 0.1 cdot 10^{-3} space м^3$
$F_{А1} — ?$
$F_{А2} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Рассчитаем архимедову силу, которая будет действовать на кусок железа в воде:
$F_{А1} = g rho_1 V$,
$F_{А1} = 9.8 frac{Н}{кг} cdot 1000 frac{кг}{м^3} cdot 0.1 cdot 10^{-3} space м^3 = 0.98 space Н approx 1 space Н$.
Теперь рассчитаем архимедову силу, которая будет действовать на кусок железа в керосине:
$F_{А2} = g rho_2 V$,
$F_{А2} = 9.8 frac{Н}{кг} cdot 800 frac{кг}{м^3} cdot 0.1 cdot 10^{-3} space м^3 = 0.784 space Н approx 0.8 space Н$.
Ответ: $F_{А1} approx 1 space Н$, $F_{А2} approx 0.8 space Н$.
Упражнение №4
Бетонная плита объемом $2 space м^3$ погружена в воду. Какую силу необходимо приложить, чтобы удержать ее в воде; в воздухе?
Дано:
$V = 2 space м^3$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1000 frac{кг}{м^3}$
$rho_2 = 1.29 frac{кг}{м^3}$
$rho_б = 2300 frac{кг}{м^3}$
$F_1 — ?$
$F_2 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Бетонная плита находится в воде. На нее действует сила тяжести и архимедова сила. Они направлены противоположно друг другу и будут иметь разные величины. Разность этих сил — и будет искомая сила $F_1$, которую нужно приложить, чтобы удержать бетонную плиту в воде (чтобы она не опускалась на дно и не всплывала):
$F_1 = F_{тяж} space − space F_{А1}$.
Сила тяжести рассчитывается по формуле:
$F_{тяж} = gm$.
Массу бетонной плиты мы можем выразить через ее плотность и объем:
$m = rho_б V$,
$F_{тяж} = g rho_б V$.
Архимедова сила, действующая на бетонную плиту в воде:
$F_{А1} = g rho_1 V$.
Подставим силу тяжести и архимедову силу в формулу и рассчитаем $F_1$:
$F_1 = F_{тяж} space − space F_{А1} = g rho_б V space − space g rho_1 V = gV cdot (rho_б space − space rho_1)$,
$F_1 = 9.8 frac {Н}{кг} cdot 2 space м^3 cdot (2300 frac{кг}{м^3} space − space 1000 frac{кг}{м^3}) = 25 space 480 space Н approx 25 space кН$.
Используем ту же формулу для того, чтобы рассчитать силу $F_2$, которую нужно приложить, чтобы удержать бетонную плиту в воздухе:
$F_2 = gV cdot (rho_б space − space rho_2)$,
$F_2 = 9.8 frac {Н}{кг} cdot 2 space м^3 cdot (2300 frac{кг}{м^3} space − space 1.29 frac{кг}{м^3}) approx 45 space 054 space Н approx 45 space кН$.
Ответ: $F_1 approx 25 space кН$, $F_2 approx 45 space Н$.
Упражнение №5
Предположив, что корона царя Гиерона в воздухе весит $20 space Н$, а в воде — $18.75 space Н$, вычислите плотность вещества короны. Полагая, что к золоту было подмешано только серебро, определите, сколько в короне было золота и сколько серебра. При решении задачи плотность золота считайте равной $20 space 000 frac{кг}{м^3}$, плотность серебра — $10 space 000 frac{кг}{м^3}$. Каков был бы объем короны из чистого золота?
Дано:
$P_1 = 20 space Н$
$P_2 = 18.75 space Н$
$rho_з = 20 space 000 frac{кг}{м^3}$
$rho_с = 10 space 000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
$rho_1 = 1.29 frac{кг}{м^3}$
$rho_2 = 1000 frac{кг}{м^3}$
$rho — ?$
$m_з — ?$
$m_с — ?$
$V_1 — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Вес короны в воздухе $P_1$ будет меньше веса тела в вакууме $P$ на архимедову силу $F_{A1}$. То есть:
$P_1 = P space − space F_{A1}$.
Значит, вес короны в вакууме будет равен сумме ее веса в воздухе и архимедовой силы:
$P = P_1 space + space F_{А1}$,
$gm = P_1 space + space g rho_1 V$.
Теперь запишем такое же уравнение для веса короны в воде:
$gm = P_2 space + space g rho_2 V$.
Левые части уравнений у нас равны, поэтому мы можем приравнять правые части друг к другу:
$P_1 space + space g rho_1 V = P_2 space + space g rho_2 V$.
Перенесем элементы, содержащие неизвестный объем вправо:
$P_1 space − space P_2 = g rho_2 V space − space g rho_1 V$,
$P_1 space − space P_2 = gV (rho_2 space − space rho_1)$.
Выразим отсюда объем короны и рассчитаем его:
$V = frac{P_1 space − space P_2}{g (rho_2 space − space rho_1)}$,
$V = frac{20 space Н space − space 18.75 space Н}{9.8 frac{Н}{кг} (1000 frac{кг}{м^3} space − space 1.29 frac{кг}{м^3})} = frac{1.25}{9787} space м^3 = 12.8 cdot 10^{-5} space м^3$.
Используем одно из первых уравнений для веса короны в вакууме и в воздухе:
$gm = P_1 space + space g rho_1 V$.
Выразим отсюда массу короны и рассчитаем ее:
$m = frac{P_1 space + space g rho_1 V}{g}$,
$m = frac{20 space Н space + space 9.8 frac{Н}{кг} cdot 1.29 frac{кг}{м^3} cdot 12.8 cdot 10^{-5} space м^3}{9.8 frac{Н}{кг}} approx 2.04 space кг$.
Теперь мы знаем массу и объем короны. Рассчитаем ее плотность:
$rho = frac{m}{V}$,
$rho = frac{2.04 space кг}{12.8 cdot 10^{-5} space м^3} approx 16 space 000 frac{кг}{м^3}$.
Корона состоит из серебра и золота. Это означает, что ее общий объем мы можем записать в виде суммы объемов серебра и золота, ее составляющих:
$V = V_с space + space V_з$.
То же самое с общей массой короны:
$m = m_с space + space m_з$.
Запишем объемы через массы и плотности (а также выразим массу золота через общую массу короны и массу серебра):
$V_с = frac{m_с}{rho_с}$,
$V_з = frac{m_з}{rho_з} = frac{m space − space m_с}{rho_з}$.
Подставим эти объемы в формулу для общего объема короны и выразим из нее массу серебра:
$V = frac{m_с}{rho_с} space + space frac{m space − space m_с}{rho_з} = frac{m_с (rho_з space − space rho_с) space + space rho_с m}{rho_с rho_з} = m_с cdot frac{rho_з space − space rho_с}{rho_с rho_з} space + space frac{m}{rho_з}$,
$m_с = frac{V space − space frac{m}{rho_з}}{frac{rho_з space − space rho_с}{rho_с rho_з}} = frac{rho_с (V rho_з space − space m)}{rho_з space − space rho_с}$.
Рассчитаем массу серебра, содержащегося в короне:
$m_с = frac{10 space 000 frac{кг}{м^3} (12.8 cdot 10^{-5} space м^3 cdot 20 space 000 frac{кг}{м^3} space − space 2.04 space кг)}{20 space 000 frac{кг}{м^3} space − space 10 space 000 frac{кг}{м^3}} = frac{5200 frac{кг^2}{м^3}}{10 space 000 frac{кг}{м^3}} = 0.52 space кг$.
Теперь мы можем вычислить и количество золота в короне:
$m_з = m space − space m_с$,
$m_з = 2.04 space кг space − space 0.52 space кг = 1.52 space кг$.
Если бы вся корона была из золота, то ее объем был бы равен:
$V_1 = frac{m}{rho_з}$,
$V_1 = frac{2.04 space кг}{20 space 000 frac{кг}{м^3}} = 10.2 cdot 10^{-5} space м^3$.
Ответ: $rho approx 16 space 000 frac{кг}{м^3}$, $m_з = 1.52 space кг$, $m_с = 0.52 space кг$, $V_1 = 10.2 cdot 10^{-5} space м^3$.
Упражнение №6
По мелким камешкам ходить босыми ногами больно. Почему человек не испытывает боли, если ходит по таким же камням в воде?
Посмотреть ответ
Скрыть
Ответ:
Что означает фраза «ходить по камням»? Со стороны физики, когда мы наступаем на камни, мы давим на них своим весом: $p = frac{F}{S} = frac{P}{S}$.
Когда мы оказываемся в воде, наш вес уменьшается. Это следствие действия на нас архимедовой силы. Уменьшается вес — уменьшается и давление наших стоп на камни.
Добрый день !
С большим опозданием подключаюсь к теме.
За рубежом-то есть практика применения «массы в воздухе» и «массы в вакууме». Если ваша компания отгружает н/п на экспорт, в накладной вы увидите две массы в тоннах: «MT in AIR» и «MT in VAC» (налог платится с массы в вакууме). Импортные tank- и flow-компьютеры имеют функции вычислений «массы в воздухе» для сопоставления результатов измерения в резервуарах и с помощью расходомеров с весами. Например в руководстве на систему учёта резервуарных запасов Entis указано следующее:
«IX.1 РАСЧЕТ ПЛОТНОСТИ (СТАНДАРТНОЙ)
Вы можете выбрать расчет массы в атмосфере или закрытом объеме. Этот
выбор производится в экране <F4> Данных продукта в Глобальной
Установке (смотри страницу 18).
Если вы выберите ~In Air~, ENTIS получит фактор коррекции, так что
расчет может быть сравнен с весом продукта на весах — он компенсируется
стандартной медной гирькой в воздухе.
Если вы выберите ~In Vacuo~, ENTIS применит следующую формулу:
Mass (in vacuo) = Final Vol x Ref Dens
Final Vol — это G.S.V. если нет коррекции чистого объема, T.G.S.V.
если есть коррекция паров ы свободном объеме, N.S.V. если есть
коррекция на содержание осадка и воды.
Ref Dens берет значение, которое вы ввели на экране <F4> Данных
продукта в Глобальной Установке (смотри страницу 18), или измерение
плотности погружением от 854, если вы имеете эту функцию.
Для преобразования Массы рассчитанной в закрытом объеме для атмосферы,
ENTIS прибегает к следующей формуле:
Mass (in vacuo) x (Ref Dens — Air Density)
Mass (in air) = ——————————————
Ref Dens
В этом расчете Air Density — это значение, которое вы вводите на
экране Данных системы в Глобальной Установке (смотри руководство
Технолога).»
Хочу уточнить, что при взвешивании СУГ и т.п. поправку на потерю веса в воздухе применять не нужно — в отличие от нефтепродуктов, порожняя цистерна с СУГ герметично закрыта под избыточным давлением и налив тоже производится герметично. Выталкивающая сила, равная произведению объёма закрытой цистерны на плотность воздуха, одинакова для наполненной и для порожней цистерны (для цистерн с СУГ есть небольшая тонкость- неизвестно, какая масса газовой фазы была в порожней цистерне и какая стала в наполненной. Чтобы точно знать, какую массу углеводородов продали, нужно бы знать и изменение массы газовой фазы).
Если вы работаете в нефтеперерабатывающей компании, вы наверное, знаете зарубежную компанию HSB Solomon Associates LLC, которая занимается различными вопросами НПЗ — исследованиями,анализом деятельности,эффективностью, потерями и пр. Solomon обращает внимание на потерю веса в воздухе и учитывает «массу в вакууме» при расчёте потерь НПЗ, если продукты отгружаются по весам.
Измерение массы (точное взвешивание)
Цель работы:
изучить методы измерения массы и
приобрести умение работы с аналитическими
весами.
Приборы и
принадлежности: весы аналитические,
разновес, взвешиваемое тело с известной
плотностью.
Теория метода
Масса
тела m
есть физическая величина, являющаяся
мерой инертности тела в поступательном
движении. Отношение масс двух тел равно
отношению их весов. На этом основано
сравнение масс тел с помощью рычажных
весов.
Рычажные весы
представляют собой равноплечный или
неравноплечный рычаг, свободно качающийся
на опоре или подвесе. Основным соотношением,
которое позволяет найти неизвестную
массу тела, является условие равенства
нулю моментов сил, действующих на рычаг
в положении равновесия.
Если
на одном плече рычага подвешен груз с
неизвестной массой m,
а на другом – уравновешивающий его
эталонный груз m1,
то в положении равновесия
(1)
где
Р
– вес тела неизвестной массы; Р1
– вес разновеса; FA
и
— архимедовы силы, действующие
соответственно на груз и разновес в
воздухе;
— длины плеч коромысла.
Подставляя выражение для веса в формулу (1), получаем
.
(2)
Если
плечи рычага весов равны
,
то выражение (2) упрощается:
.
(3)
Вес тела в этом
случае будет равен
.
(4)
Так
как идеально равноплечные весы изготовить
технически невозможно, то неравноплечность
всегда вносит в результат некоторую
ошибку. Устранение этой ошибки при
точном взвешивании достигается
применением специальных способов
взвешивания.
Как
уже отмечалось выше, равновесие рычага
весов наступает не при равенстве масс
тела и разновеса, а при условии равенства
разностей веса и архимедовой силы для
тела и разновеса. Величину поправки,
которая устраняет ошибку в определении
массы, вызванную потерей веса тела в
воздухе, легко найти из следующих
вычислений:
,
(5)
где
Р
– вес тела в вакууме; Р1
– вес разновеса в вакууме; V
и V1
– объемы
тела и разновеса;
— плотность
воздуха.
Для объемов тела
и разновеса можем написать
V=;V1=
;
где
m и— соответственно масса и плотность тела;m1и
— масса и плотность разновеса.
Подставив выражения
для объемов тел в формулу (5), получим
,
(6)
или
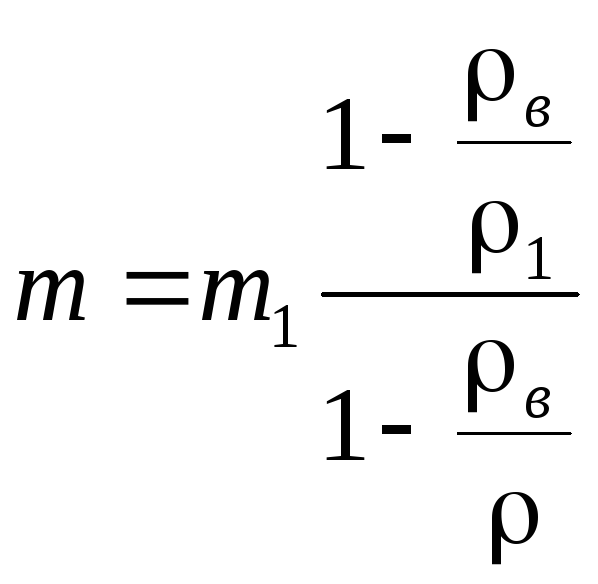
(7)
Учитывая,
что
и
,
получаем окончательную формулу:

(8)
Откуда следует,
что поправка на действие архимедовой
силы равна
.
(9)
Для
взвешивания небольших тел с высокой
точностью (до десятых долей миллиграмма)
применяются аналитические весы (рис.1).
Основной частью аналитических весов
является равноплечный рычаг ВВ,
называемый коромыслом, опорой которого
служит ребро закаленной призмы а,
находящейся в середине коромысла и
опирающейся на агатовую полированную
пластинку, укрепленную наверху колонки
А.
На концах коромысла имеются призмы bb,
служащие для подвешивания чашек СС.
Если на чашках нет грузов, то коромысло
должно устанавливаться горизонтально.
Для определения положения кор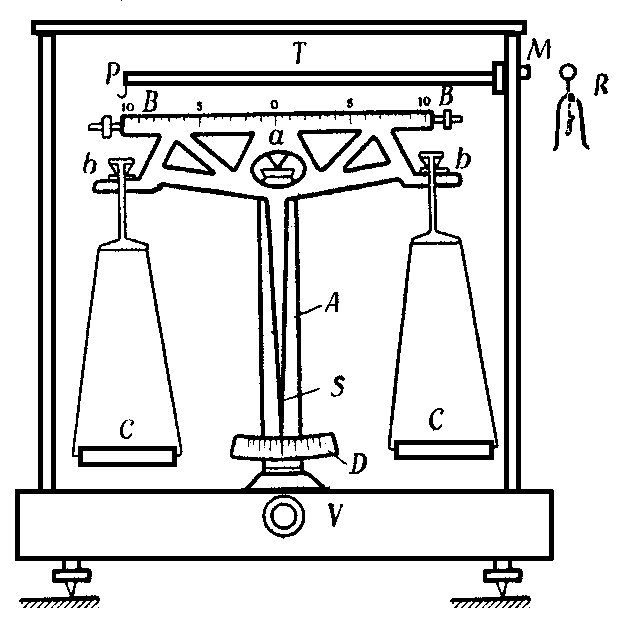
служит длинная стрелкаS,
прикрепленная к его середине.
Рис.1
Конец
стрелки S
движется перед шкалой D,
находящейся у основания колонки А.
При горизонтальном положении коромысла
стрелка должна указывать на среднее
деление шкалы.
Когда
весы не находятся в работе, их необходимо
арретировать. Это производится действием
особого приспособления внутри колонки
весов, при помощи которого коромысло и
чашки несколько приподнимаются вверх,
вследствие чего их призмы освобождаются
от давления. Арретирование производится
посредством вращения головки V
в ту или иную сторону.
При
взвешивании используются специальные
разновески, масса которых известна и
указана на них. Чтобы не употреблять
разновесок меньше 10 шт, пользуются так
называемым рейтером R,
представляющим собой тонкую проволоку,
согнутую в виде крючка (с ушком). Рейтер
помещается на одно из плеч коромысла,
разделенное обычно на 10 равных частей.
Помещение и снятие рейтера производятся
особым приспособлением. Оно состоит из
стержня Т,
проходящего сквозь правую боковую
стенку ящика весов и перемещающегося
параллельно коромыслу. Стержень может
вращаться вокруг своей оси; на внешнем
конце он снабжен головкой М,
а на внутреннем – боковым рычажком Р
и выступающим штифтом; этот последний
вводится в ушко рейтера и подхватывает
его. Помещение рейтера на первое, второе,
третье и т.д. деления плеча коромысла,
считая от середины, равносильно действию
положенного на чашку груза 1, 2, 3 и т.д.
шт.
При обращении с
аналитическими весами необходимо
соблюдать следующие правила:
1. Пока весы не
арретированы, нельзя класть на чашки
или снимать с них груз (не следует даже
прикасаться к чашкам), нельзя производить
остановку рейтера на коромысле весов.
2. Грузы следует
накладывать на чашку весов так, чтобы
общий центр тяжести грузов проходил по
середине чашки.
3. Разновески брать
и укладывать на чашки весов только при
помощи пинцета.
4. Снимая разновески
с весов, следует их класть непременно
в ящик каждую на определенное ей место.
5. Не следует
полностью освобождать коромысло, пока
чашки весов еще мало уравновешены, его
освобождают лишь на столько, чтобы можно
было судить, которая из чашек легче,
замечая при этом, куда отклоняется
стрелка; после этого тотчас следует
арретировать коромысло и прибавлять
или убавлять разновески. При малой
разнице между весами взвешиваемого
тела и разновесок коромысло начинает
уже маятникообразно качаться.
6. Освобождать и
арретировать коромысло следует всегда
медленно и плавно; если весы качаются,
то арретировать надо весьма осторожно,
в то время когда стрелки проходят через
положение равновесия, иначе коромысло
получит толчок.
7. Если чашки
качаются маятникообразно, то прежде
следует успокоить прикосновением листка
бумаги к их краю и уже только после этого
полностью освободить коромысло.
8. При наблюдении
качания весов дверцы их должны быть
непременно закрыты.
9. Если по освобождении
коромысла окажется, что амплитуда
колебаний слишком мала (менее 3-4 деления
в ту или другую сторону), то, притворив
слегка дверцу, можно махнуть перед
весами рукой, тогда струя воздуха
обыкновенно сообщает коромыслу
достаточную амплитуду.
10. Не следует
оставлять надолго груз на чашках,
особенно когда весы не арретированы;
когда взвешивание окончено, весы надо
арретировать, нагрузки снять и закрыть
дверцы.
Для того, чтобы
произвести взвешивание на аналитических
весах, необходимо:
-
определить нулевую
точку весов; -
определить
чувствительность весов; -
произвести
взвешивание; -
ввести поправку
на потерю веса в воздухе; -
ввести поправку
на неравенство плеч коромысла.
Определение
нулевой точки весов.
Нулевой точкой (точкой равновесия) весов
называется то деление, на котором при
отсутствии трения останавливается
указатель стрелки, когда коромысло
перестает колебаться.
Н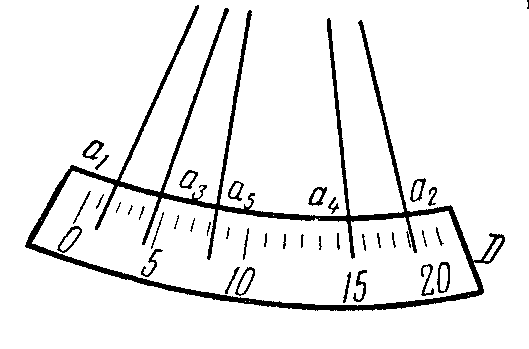
точку весов определяют по методу качаний.
Осторожно освободив коромысло и пропустив
несколько колебаний, замечают положение
конца стрелки в моменты наибольших
отклонений по шкалеD
(рис.2).
Рис.2
Вследствие
трения колебания постепенно затухают.
Обычно нулевая точка ненагруженных
весов определяется из пяти колебаний:
берутся три отсчета в одну и другую
сторону. Если а1,
а2,……а5
– последовательные
отсчеты влево, и а1,
а2,……а5
– последовательные
отсчеты вправо, то нулевая точка N0
находится из формулы

(10)
Определение
чувствительности весов.
Отношение числа делений шкалы n,
на которое смещается стрелка весов, к
весу перегрузка, вызвавшего его смещение,
называется чувствительностью весов.
Для
того, чтобы определить чувствительность
весов, помещают рейтер на первое деление
шкалы коромысла, что соответствует
нагрузке в 1 мг и находят, как и для
ненагруженных весов, новое положение
равновесия
Тогда
чувствительность весов найдется как
разность между
и N0
n=—N0
. (11)
Взвешивание.
При взвешивании тело помещают на левую
чашу весов, а на правую — гирьку из
разновеса. Сначала нужно попытаться
уравновесить тело граммовыми гирями;
если вес тела не выражается целыми
граммами, то необходимо продолжать
уравновешивать с помощью дециграммов
и сантиграммов. Если не удается
уравновесить тело и с помощью сантиметровых
гирек, то необходимо использовать
рейтер, догружая весы миллиграммами.
Перемещая рейтер по шкале на коромысле,
можно найти два таких его положения, в
одном из которых вес разновеса и рейтера
будет больше веса тела, а в другом —
меньше.
Пусть
значение отклонения стрелки N1
соответствует недогрузке правой чаши
весов. Следовательно, значение N1
лежит правее ранее найденного значения
N0
(нулевой точки), а N2
(значение отклонения стрелки при
перегрузке правой чаши весов) будет
лежать левее N0.
Пусть
значение N1
соответствует весу Р
мг. Тогда значение N2
будет соответствовать весу (Р+1)
мг. Таким
образом, для приведения весов к нулевой
точке веса Р
мг недостаточно, а (Р+1)
мг много.
Необходимо добавить к весу Р
мг добавочный груз
мг,
чтобы уравновесить весы.
Так
как разновесу в 1 мг соответствует
отклонение (N1-N2),
то вес Х
вызовет отклонение: N1-N0.
Из пропорции находим
или
.
(12)
Таким
образом, искомый вес тела Р1
будет складываться из веса разновесок
на
правой чашке весов, веса рейтерадля
значенияN1
и добавочной нагрузки Х,
вычисляемой по формуле (12):
Р1=(+
+
)
мг. (13)
Поправку
на кажущуюся потерю веса
в воздухе определяют из формулы (9). Но,
учитывая, что разница между кажущимся
и истинным весом не превышает 0,2%, на
практике часто ограничиваются определением
только кажущегося веса.
Неточность
определения массы, вызванная неравенством
плеч коромысла, можно устранить методом
двойного взвешивания (методом Гаусса).
Суть метода состоит в том, что производят
два взвешивания: при первом взвешивании
испытуемое тело помещают на левую чашу
весов, а при втором – на правую.
При первом
взвешивании для веса тела Ри веса
разновесокР1по теореме
моментов справедливо равенство
,
(14)
где
—
длина левого плеча;— длина правого плеча. Для второго
взвешивания-
.
(15)
Из (14) и (15) находим,
что
,
(16)
или
,
(17)
т.е.
масса тела равна среднему геометрическому
из произведения масс разновесок при
первом и втором взвешивании.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
