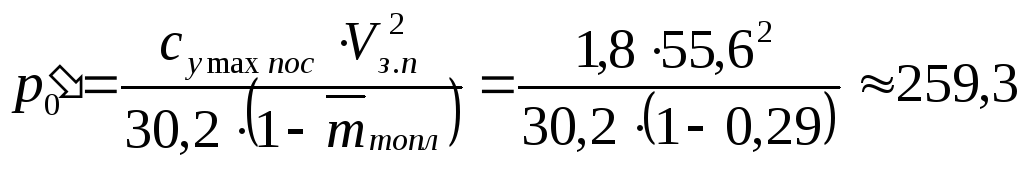Как найти массу в полете

Для расчёта воспользуемся методом
последовательных приближений (итераций),
применять вначале приближенные, а затем
все более уточненные методы и формулы
для расчетов.

3.1. Исходные данные для расчета основных параметров самолета

В ходе расчета основных параметров
проектируемого самолета понадобятся
некоторые его данные.

В качестве исходных данных будут:

L_расч –
расчетная дальность полета самолета,
L_расч = 2000
км (ТЗ);

М_крейс – крейсерское
число Маха полета, М_крейс
= 0,8…0,85 (ТЗ);

К_крейс – качество самолета
на крейсерском режиме, К_крейс
≈ 10 (статистика);

с_Р – удельный расход
топлива, с_Р ≈ 0,71 кг/(кгс·ч)
(данные двигателя);

V_з.п –
скорость захода на посадку, V_з.п
= 200…230 км/ч (ТТТ и по статистике);

Н_крейс – крейсерская
высота полета, Н_крейс =
11000 м (ТТТ);

V_крейс –
крейсерская скорость полета, V_крейс
= 850 км/ч (ТТТ);

с_{у крейс} – коэффициент
подъемной силы на крейсерском режиме,
с_{у крейс} = 0,4 (статистика);

с_{у тах пос} – максимальный
коэффициент подъемной силы при посадке,
с_{у тах пос} = 1,8 (статистика);

с_{у тах взл} – максимальный
коэффициент подъемной силы при взлете,
с_{у тах взл} = 1,3 (статистика);

l_разб –
длина разбега, l_разб
= 500 м (ТТТ);

К_тах – максимальное
качество самолета, К_тах
≈ 10…12 (статистика);

V_пос –
посадочная скорость, V_пос
= 180…200 км/ч (ТТТ);

с_удоп – допустимый
коэффициент подъемной силы, с_удоп
= 0,9 (статистика);

f_разб –
коэффициент трения о ВПП при разбеге,
берется по статистике в зависимости от
поверхности ВПП;

– эксплуатационная перегрузка,

(ТТТ).

3.2. Первое приближение

Последовательность определения
параметров самолета в процессе
проектирования диктуется их
взаимозависимостью, поэтому расчет
будем осуществлять в следующем
нижеприведенном порядке.

3.2.1. Расчет массы самолета т₀
в первом приближении

Перед тем как приступить к определению
основных параметров самолета, рассчитаем
его массу в 1-м приближении.

Взлетная масса представляет собой
сумму:

, (3.1)

где m_констр
= f₁ (m₀,
параметры крыла) – масса конструкции;
m_с.у = f₂
(m₀, параметры
силовой установки) – масса силовой
установки; m_об.упр
= f₃ (m₀,
параметры оборудования управления и
всего самолета) – масса оборудования
и управления; m_топл
= f₄ (m₀,
V, L,
H, c_P,
K=c_y/c_x,
режим полета) – масса топлива; m_ц.н
= const – заданная
целевая нагрузка; m_сл
= const – известная
служебная нагрузка и снаряжение.

Зависимость т_констр,
т_с.у, т_об.упр
от т₀ весьма сильная и
сложная, зависимость т_топл
от т₀ практически линейная.
В результате получается сложное
трансцендентное уравнение, которое
невозможно решить относительно т₀
в явном (конечном) виде. Выход из этого
затруднения при расчете взлетной массы
первого приближения следующий.

Чтобы уменьшить влияние т₀
на т_констр, т_с.у,
т_об.упр, т_топл,
разделим обе части (3.1) на т₀,
получим:

. (3.2)

Относительные величины
,
,

слабее зависят от т₀, чем
абсолютные их значения;

не зависит от т₀.

Если принять (,
,
,)
= const по статистике,
то из (3.2) получим взлетную массу в первом
приближении:

. (3.3)

Таким образом, зададимся значениями
величин
,
,
,

по статистике (см., например, [1,
табл. 6.1 на стр.]).
Примем:

;

;

;

.

Значение т_ц.н и т_сл
берутся из ТЗ. Здесь следует отметить,
что проектируемый самолет является
учебно-тренировочным, и этот самолет
из принятой нами концепции никакой
целевой нагрузки (пушки, ракеты, бомбы,
подвесные топливные баки) не несет
(если, конечно, в качестве целевой
нагрузки не рассматривать обучаемого
курсанта). Таким образом, примем в
расчетах, что:

т_ц.н + т_сл
= 200 кг (берется по 100 кг на каждого
летчика).

Тогда

кг.

3.2.2. Расчет относительной массы
расходуемого в полете топлива

где L – дальность
крейсерского полета, км; с_Ркр
– удельный расход топлива в крейсерском
полете, кг/(кгс·ч); К_кр –
аэродинамическое качество самолета в
крейсерском полете, V_кр
– заданная крейсерская скорость, км/ч;
k_топл –
статистический коэффициент, учитывающий
навигационный запас топлива и топлива
на планирование (снижение) самолета с
крейсерской высоты полета, k_топл
= 0,22…0,18 для L ≤ 3500 км.

Относительная масса топлива
,
необходимого на набор крейсерской
высоты и скорости полета, определяется
по формуле:

,

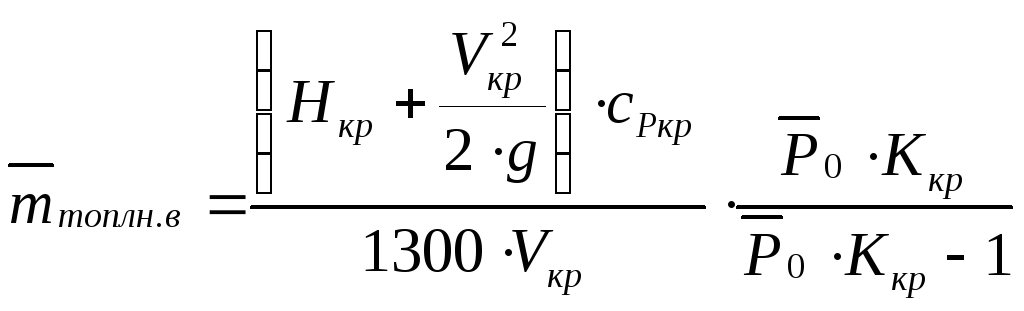
где Н_кр и V_кр
– крейсерская высота и скорость, м и
м/с соответственно; g
= 9,81 м/с² – ускорение свободного
падения;

– стартовая тяговооруженность
(принимается из ТЗ или по самолетам
прототипам).

Примем: L = 2000 км; с_Ркр
= 0,91 кг/(кгс·ч) (для крейсерского полета);
К_кр = 10, V_кр
= 850 км/ч ≈ 236,1 м/с; k_топл
= 0,2; Н_кр = 11000 м,
.
Тогда:

;

.

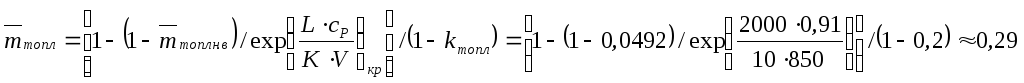
3.2.3. Расчет величины стартовой удельной
нагрузки на крыло р₀

Расчет р₀ определяется из
следующих условий:

а) из условия посадки самолета:

.

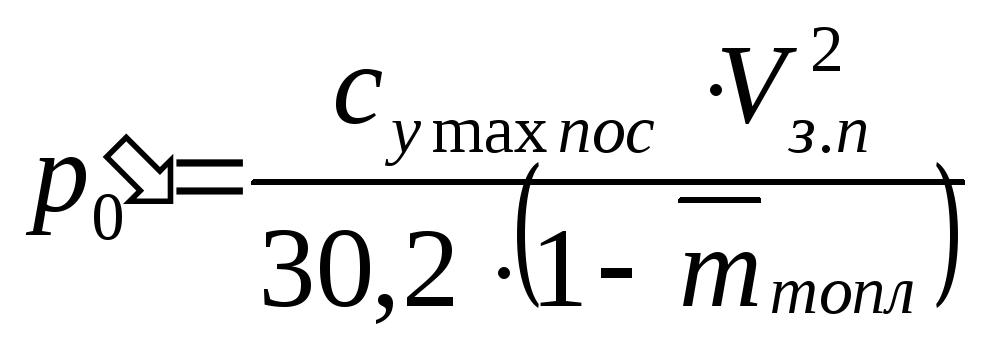
Здесь V_з.п
в м/с, а величина с_{у тах пос}
берется по статистике в зависимости от
механизации крыла. Значение

рассчитано выше в п. 3.2.2.

Примем: V_з.п
= 200 км/ч ≈ 55,6 м/с, с_{у тах пос}
= 1,8 (для слабой механизации). Тогда:

даН/м².

б) из условия обеспечения заданной
крейсерской скорости полета:

.

Здесь

– скоростной напор, который берется
для скорости, соответствующей числу М
= 1 на заданной высоте полета (или
соответствует величине а – скорости
звука на этой высоте); с_{у крейс}
– коэффициент подъемной силы в крейсерском
полете, берется по статистике. Значение


рассчитано выше в п. 3.2.2.

Имеем высоту полета Н = 11000 м, на
которой плотность воздуха ρ = 0,365
кг/м³, скорость звука а = 295,2
м/с. Тогда:

Н/м²;

.

Также примем, что с_{у крейс}
≈ 0,4, тогда:

Н/м².

Или

даН/м².

в) из условия заданной маневренности:

Для маневренного самолета нагрузка на
крыло определяется и с учетом полета
на допускаемых коэффициентах подъемной
силы и эксплуатационной перегрузки:

.

Здесь с_удоп определяется
либо по срыву обтекания, либо по тряске,
либо по бафтингу. Берется по статистике.
Величина n_удоп
определяется либо прочностью самолета
(),
либо физиологическими возможностями
летчика. Значение

рассчитано выше в п. 3.2.2.

Примем с_{у доп} ≈ 0,9, п_у
доп = 6.

Величина q_маневр
– скоростной напор на «рабочих»
скорости и высоте полета. Считаем, что
проектируемый самолет «работает»
на высоте Н = 6000 м (давление на этой
высоте р_Н = 47210 Па) на числах
Маха М =0,65, тогда

даН/м².

В итоге

даН/м².

Для проектируемого самолета принимается
минимальная из найденных величин
стартовая удельная нагрузка на крыло:

Имеем в итоге:

даН/м².

3.2.4. Расчет стартовой тяговооруженности
самолета

Расчет

осуществляется из следующих условий:

а) из условия набора высоты при одном
отказавшем двигателе по формуле:

.

Так как на самолете один двигатель, то
данный пункт не рассматриваем

б) из условия обеспечения горизонтального
полета на высотах Н ≥ 11000 м:

.

Величина К_крейс берется
по статистике, К_крейс ≈
(0,85…0,95) К_тах.

Коэффициент φ_руд учитывает
степень дросселирования двигателя в
крейсерском полете до режима,
соответствующего неограниченному
времени работы двигателя, или до режима,
соответствующего оптимальному расходу
топлива. Обычно он принимается равным
0,8…0,9.

Δ – относительная плотность воздуха,
для высоты Н = 11000 м Δ = 0,297.

Коэффициент ξ учитывает изменение
тяги по скорости полета, и для М<1
можно принять ξ = 1.

Имеем К_крейс = 10, ξ = 1,
φ_руд = 0,85, Δ = 0,297, тогда

.

в) из условия обеспечения заданной длины
разбега самолета при взлете

.

Значение стартовой удельной нагрузки
на крыло р₀ было найдено
в п. 3.2.3. Остальные величины берутся из
статистики и даны в п. 3.1.

Имеем: l_разб
= 500 м – длина разбега; с_{у тах
взл} ≈ 1,3 (по статистике); К_разб
≈ 6 – аэродинамическое качество при
разбеге; f_разб
= 0,03 – коэффициент трения колес шасси
при разбеге (см. [1, стр.,
взято для мокрого бетонного покрытия);
р₀ = 253,7 даН/м². Тогда

г) из условия заданной скороподъемности

,

где V_у –
заданная вертикальная скорость; V
– заданная или наивыгоднейшая скорость
полета.

Примем V_y
= 100 м/с у земли, V = 700
км/ч ≈ 195 м/с, К_тах ≈ 11; ξ
= 1 для М<1; φ_руд = 1,
если полет идет на бесфорсажном режиме.
Коэффициент φ_Н для высоты
Н < 11000 м равен:
.
Для высоты Н = 0 м Δ = 1. Тогда

.

д) из условия заданной максимальной
скорости полета на заданной высоте

.

Значение с_х0 берется по
статистике и примем с_х0 ≈
0,04; значение стартовой удельной нагрузки
на крыло р₀ было найдено
в п. 3.2.3. Значение q_max
берем для высоты полета Н = 6000 м и
скорости полета V =
900 км/ч ≈ 250 м/с, тогда

даН/м².

Значение коэффициентов ξ, φ_Н
и φ_руд такие же, как и
ранее, (Δ = 0,537 для Н = 6 км) тогда

.

е) из условия полета с заданной
установившейся эксплуатационной
перегрузкой

при заданных V и Н

По статистике примем

(см. [1, стр.]). Также примем,
что К_тах ≈ 11. Высоту берем
Н = 11000 м. Коэффициент φ_Н
для высоты Н ≥ 11000 м равен:
.
Для высоты Н = 11000 м Δ = 0,297. Значения
коэффициентов ξ и φ_руд
такие же, как и ранее, тогда

Для проектируемого самолета принимается
максимальная из найденных величин
стартовая тяговооруженность:

В итоге получим:

.

3.2.5. Расчет основных параметров самолета
в абсолютных величинах

Из выше приведенных расчетов получили:

кг;

даН/м²;
.

Зная эти величины, получим основные
абсолютные параметры самолета.

Площадь крыла будет:

,

где удельная нагрузка на крыло р₀
имеет размерность даН/м². Тогда

м².

Взлетная тяга двигателей будет:

даН.

Таким образом, заканчивается первая
итерация выбора основных параметров
самолета. Далее производится расчет
массы самолета во втором приближении,
и весь процесс выбора основных параметров
повторяется вновь.

Соседние файлы в папке Текст

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Масса

Масса обозначается символом (m ), является скалярной величиной и в СИ измеряется в килограммах.

Иногда массу в условии некоторых задач задают в граммах или, например, в тоннах. Чтобы перевести массу в килограммы, используют такие формулы:

[ large boxed{ begin{matrix} m = left( text{тонны} right) cdot 10^{3} left( text{кг}right) \ m = left( text{центнеры} right) cdot 10^{2} left( text{кг}right) \ m = left( text{граммы} right) cdot 10^{-3} left( text{кг}right) \ m = left( text{миллиграммы} right) cdot 10^{-6} left( text{кг}right) \ end{matrix}} ]

• ( large text{(тонны)} ) – подставьте количество тонн вместо этой скобки;
• ( large text{(центнеры)} ) – вместо этой скобки подставьте количество сотен килограммов;
• ( large text{(граммы)} ) – подставьте количество граммов вместо этой скобки;
• ( large text{(миллиграммы)} ) – вместо этой скобки подставьте количество миллиграммов;

От массы зависят инерционные и гравитационные свойства физических тел.

Масса в природе проявляет себя двумя способами. Поэтому, выделяют:

1. массу инертную и
2. массу гравитационную.

Инертная масса

Масса инертная влияет на способность тела двигаться по инерции. Такая масса используется в формуле второго закона Ньютона.

Пусть два тела находятся в инерциальной системе отсчета. Если какая-либо сила одинаково ускоряет эти тела, то они обладают одинаковой инертной массой. Здесь «одинаково ускоряет» следует понимать, как «сообщает одинаковые ускорения».

Гравитационная масса

Гравитационная масса определяет силу, с которой тело притягивается к другим телам. Эта масса используется в формуле закона всемирного тяготения.

Различные эксперименты показали, что инертная и гравитационная массы равны с высокой степенью точности. Поэтому, при изучении школьной физики можно просто говорить «масса», не уточняя, о какой именно массе идет речь.

Так же, масса входит в формулы для расчета импульса и механической энергии.

Массой обладают все макроскопические тела, а, так же, такие элементарные частицы, как протоны, нейтроны, электроны и т. д. Однако, существуют и частицы, у которых нет массы покоя, например – фотоны.

Примечание: Фотон – элементарная частица, переносчик электромагнитного взаимодействия, движется со скоростью света, часто проявляет волновые свойства. Подробнее о фотонах вы узнаете в основах квантовой физики.

Сила тяжести

Сила тяжести — это сила, с которой Земля притягивает к себе тело.

(large vec{F_{text{тяж}}} left(Hright) ) — сила тяжести, она действует на тело со стороны планеты (или другого крупного небесного тела, например, астероида, или звезды).

[large vec{F_{text{тяж}}} = m cdot vec{g}]

(large m left(text{кг}right) ) — масса тела;

(large vec{g} left(frac{text{м}}{c^{2}}right) ) — ускорение свободного падения, это не постоянная величина, она может меняться. Читайте подробнее о ускорении свободного падения .

Вес

Вес – это сила. Этой силой тело давит на опору, когда опирается на нее, или растягивает подвес, когда на нем висит.

Является векторной величиной и обозначается символом (vec{P} ).

(vec{P} left(Hright) ) – вес тела, как любая сила в СИ измеряется в Ньютонах.

Вес отличается от массы. Вес, как и любая сила, измеряется в Ньютонах, а масса измеряется в килограммах.

Когда тело опирается о горизонтальную поверхность, его вес равен по модулю силе реакции опоры по третьему закону Ньютона. Поэтому, в задачах для нахождения веса удобно вычислять силу (large vec{N}). Как только мы найдем реакцию опоры (large vec{N}), мы найдем вес тела, давящего на эту опору.

Примечание: Векторы равны по модулю, когда обладают одинаковыми длинами. Так как длина вектора обозначается числом, то физики о равных по модулю векторах сил могут сказать: силы численно равны.

Чем вес отличается от силы тяжести

Вес — это сила, принадлежащая телу. А сила тяжести — это сила, действующая на тело со стороны планеты, или любого другого (крупного) тела.

Что такое невесомость

Подбросим мяч вверх и рассмотрим свободный полет мяча. Пока он в полете, он не давит на опору и не растягивает подвес. Проще говоря, мяч находится в невесомости – то есть, не имеет веса.

Масса есть всегда, а вес может отсутствовать! Как убедимся чуть позже, одна и та же масса может обладать различным весом.

Как изменяется вес тела лифте

Давайте выясним, какой вес имеет тело, находящееся в покоящемся лифте, или в лифте, который будет двигаться вверх или вниз с ускорением, или без него.

Если скорость лифта не изменяется

Сначала рассмотрим покоящийся лифт (рис. 1а), либо движущийся вверх (рис. 1б), или вниз (рис. 1в) с неизменной скоростью.

Примечание: «неизменной», также, значит «постоянной», или «одной и той же».

По первому закону Ньютона, когда действие других тел скомпенсировано, тело, не меняющее свою скорость, находится в инерциальной системе отсчета.

Как видно из рисунка, взаимодействуют два объекта: тело и опора. Тело давит своим весом на опору, а опора отвечает телу (рис. 1) силой своей реакции.

Будем записывать для рассмотренных случаев рисунка 1 векторные силовые уравнения:

[ large N – m cdot g = 0 ]

А в этой статье подробно и с объяснениями написано о том, как составлять силовые уравнения (ссылка).

Прибавив к обеим частям уравнения величину ( m cdot vec{g} ), получим

[ large N = m cdot g ]

По третьему закону Ньютона, вес тела и реакция опоры направлены противоположно и равны по модулю. Поэтому, найдя силу реакции опоры, мы автоматически находим вес тела.

Воспользуемся тем, что ( left|vec{N} right|= left|vec{P} right|), получим

[ large boxed{ P = m cdot g }]

То есть, вес тела в покоящемся лифте, или движущемся вверх или вниз с неизменной скоростью, будет равен ( mg ). Если вектор скорости лифта не изменяется ни по направлению, ни по модулю, лифт можно считать инерциальной системой отсчета.

Если скорость лифта изменяется

Теперь выясним, каким весом будет обладать тело в лифте, движущемся с ускорением (рис. 2).

Примечание: Лифт, движущийся с ускорением, не является инерциальной системой отсчета. Читайте подробнее о инерциальных системах.

Запишем силовые уравнения. Для рисунка 2а, уравнение выглядит так:

[ large N – m cdot g = m cdot a ]

А для рисунка 2б, так:

[ large N – m cdot g = — m cdot a ]

Прибавим теперь к обеим частям уравнений величину ( m cdot g ), получим:

( large N = m cdot a + m cdot g ) – для случая рис. 2а;

( large N = — m cdot a + m cdot g ) – для рис. 2б;

Вынесем массу за скобки

( large N = m cdot left( a + g right) ) – для рис. 2а;

( large N = m cdot left( -a + g right) ) – для рис. 2б;

Учтем, что ( left|vec{N} right|= left|vec{P} right|), окончательно запишем

Для рисунка 2а — движение лифта вверх с ускорением:

[ large boxed{ P = m cdot left( g + a right) }]

Вес тела в движущемся с ускорением вверх лифте, будет равен ( m cdot left( g + a right) ), то есть, превышает величину ( m cdot g ).

Когда лифт движется вниз с ускорением (рис. 2б), вес тела, наоборот — уменьшается:

[ large boxed{ P = m cdot left( g — a right) }]

Напомним, что вес в покоящемся, или движущемся вверх или вниз с неизменной скоростью лифте, в точности равен ( m cdot g ).

Вес тела в движущемся вниз с ускорением лифте, равен ( m cdot left( g — a right) ), это меньше величины ( m cdot g ).

А если при движении вниз ускорение лифта ( vec{a} ) сравняется с ускорением ( vec{g} ), то груз перестанет давить на опору и наступит состояние невесомости, вес тела будет равен нулю.

Значит, одна и та же масса может обладать разным весом, мало того, в некоторых случаях вес вообще может отсутствовать. Масса есть всегда, а вес может отсутствовать!

Что такое перегрузка

Когда вес тела больше силы тяжести, говорят, что возникает перегрузка.

[ large boxed{ P > m cdot g }]

Когда говорят о перегрузке, принято сравнивать ускорение движения вверх с ускорением свободного падения (large vec{g}).

Например, при движении ракеты с ускорением вверх, космонавт может испытывать перегрузки до 7g. Это значит, что его вес увеличивается в 7 раз.

Первый космонавт мира — Юрий Гагарин, упоминал о перегрузке: «…какая-то сила вдавливает меня в кресло все больше и больше. … трудно пошевелить рукой или ногой…».

Подобным образом мы испытываем перегрузки в самолете во время взлета — эти перегрузки вдавливают нас в кресло. Правда, эти перегрузки значительно меньше, чем перегрузки летчиков — спортсменов, или военных, летчиков — космонавтов. Представители этих профессий тренируют свое тело для того, чтобы перегрузки легче переносить.

Подведем итоги

(P = m cdot g ) — вес тела в покоящемся или движущемся вверх или вниз с постоянной скоростью лифте.

( P = m cdot left( g + a right) ) — вес, когда лифт движется с ускорением вверх;

( P = m cdot left( g — a right) ) — вес в движущемся вниз с ускорением;

Если ускорение лифта при его движении вниз ( a = g ), наступит невесомость, вес тела исчезнет ( P = 0 ).

Все свойства и параметры самолёта между собой взаимосвязаны. Математическим отображением этой взаимосвязи является уравнение баланса масс самолёта.

;

где — взлётная масса самолёта.

— масса коммерческой нагрузки.

— относительная масса крыла.

— относительная масса оперения.

— относительная масса фюзеляжа.

— относительная масса шасси.

— силовой установки.

— оборудования и управления.

— снаряжения.

— топлива.

Оценка относительной массы топлива

Определяем удельный расход топлива на взлётном режиме двигателя:

;

;

где R — взлётная тяга одного двигателя.

;

Определяем средний крейсерский удельный расход топлива при полёте с полной коммерческой нагрузкой:

;

=86,188

=1,289; K=0,869

;

Расчёт относительной массы топлива при полёте на максимальную дальность с полной коммерческой нагрузкой.

Определяем приблизительную массу топлива, расходуемого на набор высоты:

;

где — степень двухконтурности ;

Находим относительную массу топлива, расходуемого на снижение и посадку:

;

=0,01419

Определяем относительную массу аэронавигационного запаса топлива:

;

где — коэффициент запаса.

Определяем относительную массу топлива, расходуемого на крейсерском режиме полёта:

;

где ;0,484

Относительная масса топлива составляет:

;

;

Расчёт относительных масс основных частей самолёта

Определяем относительную массу крыла:

;

=0,08652

где =1- коэффициент, учитывающий разгрузку крыла силовой установкой.

=1- коэффициент, учитывающий затяжеление крыла эксплуатационно-технологическими разъёмами.

Z — степень механизированности крыла.

— относительная площадь прикорневых наплывов.

;

Определяем относительную массу оперения:

;

=0,00868

где — коэффициент демпфирования.

— коэффициент, учитывающий схему ГО.

;

;

Определяем относительную массу шасси

= 0,02=1,14.1,85,1,1.0,86=0,03673

Определяем относительную массу силовой установки полной комплектации:

Вычисляем коэффициент В_о:

;

;

Определяем относительную массу фюзеляжа:

;

где =1,59.9,62.7,13.7,13=

,,,- коэффициенты, учитывающие конструктивное исполнение фюзеляжа.

;=0,765-0,278.7,13=0,6837

;

Определяем относительную массу оборудования и управления:

;

где ;

;

;

;

Решение уравнения баланса масс

Величина взлётной массы самолёта определяется при решении методом итераций системы уравнений: решение производилось на ПЭВМ.

;

;

Расчет масс элементарных самолетах

Распределение масс между составляющими элементами укрупнённых групп самолета производится на основании статистических данных однотипных самолётов или по приближённым статистическим соотношениям.

Oпределяем массу высотного оборудования и противообледенительной системы (пос) пассажирского самолета:

;=6,791

Oпределяем массу пассажирского, бытового оборудования, декоративной обшивки фюзеляжа и теплозвукоизоляции:

;

= 12294

Oпределяем массу управления:

;

;

Oпределяем массу электрорадиоприборного оборудования:

;=284.396

;

Oпределяем массу электрооборудования:

;=130,822

;

Oпределяем массу локационного оборудования:

;=25,596

Oпределяем массу навигационного оборудования:

=34, 13

;

Oпределяем массу радиосвязного оборудования =31,283

;

Oпределяем массу приборного оборудования:

m=45,5

;

Oпределяем массу топливной системы:

;

m=2286

;

Introduction: Calculating Aircraft Weight and Balance

This instructable explains the process of finding the center of gravity for the weight and balance of an aircraft. This is an important process when piloting an aircraft because the location affects performance characteristics of the aircraft and if it is out of acceptable limits the aircraft may be uncontrollable. Having this information calculated and on hand is, in fact, a requirement for every flight you make.

What you will need:

Aircraft information manual

Paper

Pencil

Calculator

Step 1: Find Your Aircraft’s Empty Weight and Moment.

Each aircraft’s weight and moment are different. This information will be found in the Pilot’s Operating Handbook (POH) specific to the aircraft you are flying. It will be in the weight and balance chapter which is standard chapter six.

Step 2: Find Weights of Everything Loaded.

This includes pilot, all passengers, baggage, and the fuel that will be loaded into the aircraft. You will find the fuel load in the first chapter of the POH. Keep in mind that you will use the amount labeled «usable fuel» because unusable fuel is included in the aircraft’s weight and that fuel weighs six pounds per gallon.

Step 3: Calculate the Moment for the Load.

In chapter 6 of the POH you will find either a chart similar to the one on the left or a figure like the one shown on the right. If you have the chart you can follow the weight to the appropriate line to find the moment. If you have the figure, you need to multiply the weight of each position by the number given as the arm to find the moment. Calculate the moments for the pilot, all passengers, fuel, and baggage.

Example:

Using the graph above, if the pilot and front passenger weighed 300 pounds, you would find 300 on the vertical axis. You then follow that over to where it intersects the line labelled «Pilot and front passenger». You then follow that down to the horizontal axis to get your moment value of about 11. Using the other method with the same 300 pounds you would multiply by the value given for the pilot and front passenger which gives you 300*37=11,100

Step 4: Total Up the Weights and the Moments

Add together the weights for the aircraft, people, fuel, and baggage. Also add the moments found in the previous step (pilot, passengers, fuel, and baggage) to the moment of the empty aircraft.

Step 5: Determine If Center of Gravity Is Within Limits

In chapter 6 of the POH find the chart that shows the acceptable limits of the center of gravity. It will look like one of the charts pictured above. One compares the total weight to the total moment and one compares the total weight to the arm of the center of gravity. If your chart uses the arm all you need to do is divide the total moment by the total weight to find that value. If the intersection falls within the area outlined on the chart you are within acceptable limits to fly.

Example:

If your total weight was 2500 and total moment was 105 (105,000) you would find these values on their specific axes on the second chart pictured and their intersection lies within the outlined area. Using the arm you would find 105,000/2500=42 which when found on the first chart also falls withing the border.