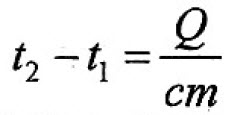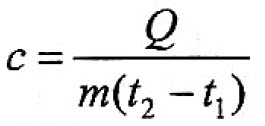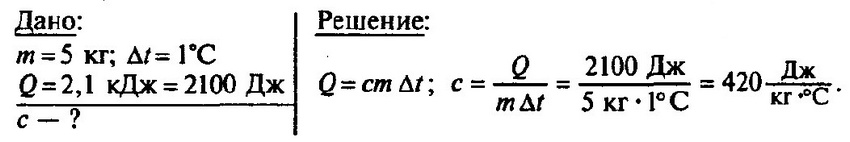Вы познакомились с понятиями количества теплоты и удельной теплоемкости. В уроке «Расчет количества теплоты, необходимого для нагревании тела или выделяемого им при охлаждении» вы познакомились с основной формулой, которую мы будем использовать и в этом уроке:
$Q = cm(t_2 — t_1)$
В данном уроке мы рассмотрим задачи на нахождение различных величин, связанных с нагреванием и охлаждением тел. При их решении вам может понадобиться таблица значений удельной теплоемкости различных веществ из прошлого урока.
Задача №1 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое для нагрева $15 space кг$ меди на $80 degree C$.
Дано:
$m = 15 space кг$
$c = 400 frac{Дж}{кг cdot degree C}$
$Delta t = 80 degree C$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Для решения этой задачи мы будем использовать формулу для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
В данном случае нам не известны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:
$Q = cm Delta t$.
Подставим значения всех величин и рассчитаем количество теплоты:
$Q = 400 frac{Дж}{кг cdot degree C} cdot 15 space кг cdot 80 degree C = 480 space 000 space Дж = 480 space кДж$.
Ответ: $Q = 480 space кДж$.
Задача №2 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое, чтобы нагреть бассейн объемом $300 space м^3$ на $10 degree C$.
В задаче идет речь о бассейне, а значит, о пресной воде. Она имеет плотность, равную $1000 frac{кг}{м^3}$. Запишем условия задачи и решим ее.
Дано:
$V = 300 space м^3$
$Delta t = 10 degree C$
$c = 4200 frac{Дж}{кг cdot degree C}$
$rho = 1000 frac{кг}{м^3}$
$c = 4200 frac{Дж}{кг cdot degree C}$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Нам неизвестна масса воды в бассейне, но известен ее объем и плотность. Плотность по определению:
$rho = frac{m}{V}$.
Тогда масса будет равна:
$m = rho V$.
Также нам неизвестны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:
$Q = c rho V Delta t$.
Рассчитаем количество теплоты:
$Q = 4200 frac{Дж}{кг cdot degree C} cdot 1000 frac{кг}{м^3} cdot 300 space м^3 cdot 10 degree C = 12.6 cdot 10^9 space Дж = 12.6 space ГДж$.
Ответ: $Q = 12.6 space ГДж$.
Задача №3 на расчет массы
Найдите массу глицерина, если при нагревании от $10 degree C$ до $15 degree C$ он поглотил $12 space кДж$ теплоты. Удельная теплоемкость глицерина равна $2430 frac{Дж}{кг cdot degree C}$.
Дано:
$Q = 12 space кДж$
$t_1 = 10 degree C$
$t_2 = 15 degree C$
$c = 2430 frac{Дж}{кг cdot degree C}$
СИ:
$Q = 12 cdot 10^3 space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Выразим отсюда массу глицерина:
$m = frac{Q}{c(t_2 — t_1)}$.
Рассчитаем:
$m = frac{12 cdot 10^3 space Дж}{2430 frac{Дж}{кг cdot degree C} cdot (15 degree C — 10 degree C)} approx 1 space кг$.
Ответ: $m approx 1 space кг$.
Задача №4 на расчет плотности
Определите плотность машинного масла объемом $1 space л$, если известно, что для увеличения температуры на $30 degree C$ ему требуется передать $45 space кДж$ теплоты. Удельная теплоемкость масла равна $1.67 frac{кДж}{кг cdot degree C}$.
Дано:
$V = 1 space л$
$Q = 45 space кДж$
$c = 1.67 frac{кДж}{кг cdot degree C}$
$Delta t = 30 degree C$
СИ:
$V = 10^{-3} space м^3$
$Q = 45 cdot 10^3 space Дж$
$c = 1.67 cdot 10^3 frac{Дж}{кг cdot degree C}$
$rho — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Нам известны изменение температуры ($Delta t = t_2 — t_1$), количество теплоты и удельная теплоемкость машинного масла. Выразим массу и рассчитаем ее:
$m = frac{Q}{c Delta t} = frac{45 cdot 10^3 space Дж}{1.67 cdot 10^3 frac{Дж}{кг cdot degree C} cdot 30 degree C} approx 0.9 space кг$.
По определению плотности:
$rho = frac{m}{V}$.
Рассчитаем плотность машинного масла:
$rho = frac{0.9 space кг}{10^{-3} space м^3} = 0.9 cdot 10^3 frac{кг}{м^3} = 900 frac{кг}{м^3}$.
Ответ: $rho = 900 frac{кг}{м^3}$.
Задача №5 на расчет удельной теплоемкости
В калориметр было налито $450 space г$ воды, температура которой $20 degree C$. Когда в эту воду погрузили $200 space г$ железных опилок, нагретых до $100 degree C$, температура воды стала равна $24 degree C$. Определите удельную теплоемкость опилок.
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “ж” для обозначения величин, связанных с железными опилками.
Дано:
$m_в = 450 space г$
$m_ж = 200 space г$
$t_{в1} = 20 degree C$
$t_{в2} = 24 degree C$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$t_{ж1} = 100 degree C$
СИ:
$m_в = 0.45 space кг$
$m_ж = 0.2 space кг$
$с_ж — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела и выделяемого при его охлаждении:
$Q = cm(t_2 — t_1)$.
Запишем эту формулу для воды:
$Q_в = c_в m_в (t_{в2} — t_{в1})$.
Запишем формулу количества теплоты для железных опилок:
$Q_ж = c_ж m_ж (t_{ж2} — t_{ж1})$.
Нагретые железные опилки помещают в воду для их охлаждения. Значит, вода будет нагреваться и поглотит некоторое количество теплоты, а опилки будут охлаждаться и выделят некоторое количество теплоты. Т.е., между этими телами будет происходить теплообмен, для которого действует уже известное вам правило:
Если между телами происходит теплообмен, то внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Это значит, что количество теплоты $Q_в$, полученное водой, будет равно количеству теплоту $Q_ж$, которое выделится при охлаждении железных опилок, но с обратным знаком: $Q_в = — Q_ж$.
Подставим выражения, которые дает формула для расчета количества теплоты:
$c_в m_в (t_{в2} — t_{в1}) = — c_ж m_ж (t_{ж2} — t_{ж1})$.
После завершения теплообмена температура воды и температура железных опилок будут равны друг другу: $t_в2 = t_ж2 = t_2$.
Подставим в наше равенство и выразим $c_ж$:
$c_ж = — frac{c_в m_в (t_2 — t_{в1})}{m_ж (t_2 — t_{ж1})}$.
Рассчитаем удельную теплоемкость железных опилок:
$c_ж = — frac{4200 frac{Дж}{кг cdot degree C} cdot 0.45 space кг cdot (24 degree C — 20 degree C)}{0.2 space кг cdot (24 degree C — 100 degree C)} = — frac{7560 space Дж}{- 15.2 space кг cdot degree C} approx 497 frac{Дж}{кг cdot degree C} approx 0.5 frac{кДж}{кг cdot degree C}$.
Ответ: $c_ж approx 0.5 frac{кДж}{кг cdot degree C}$.
Задача №6 на использование графика
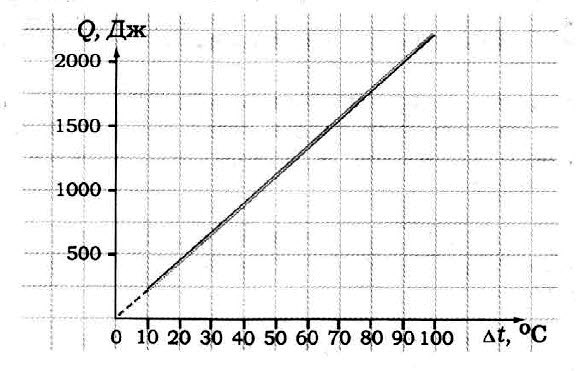
Используя график зависимости температуры керосина от сообщенного ему количества теплоты (рисунок 1), определите массу керосина.
Для начала нам нужно записать условия задачи. Из графика мы видим, что начальная температура керосина $t_1$ была равна $0 degree C$. Теперь выберем удобную нам точку на графике. Например, когда керосину сообщили количество теплоты $Q$, равное $2 space кДж$, его температура $t_2$ стала равной $10 degree C$. Теперь мы можем записать условия задачи и решить ее. Удельная теплоемкость керосина известна нам из таблицы.
Дано:
$Q = 2 space кДж$
$t_1 = 0 degree C$
$t_2 = 10 degree C$
$c = 2100 frac{Дж}{кг cdot degree C}$
СИ:
$Q = 2 cdot 10^3 space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Выразим отсюда массу:
$m = frac{Q}{c (t_2 — t_1)}$.
Рассчитаем ее:
$m = frac{2 cdot 10^3 space Дж}{2100 frac{Дж}{кг cdot degree C} cdot (10 degree C — 0 degree C)} approx 0.095 space кг approx 100 space г$.
Ответ: $m approx 100 space г$.
Задача №7 на расчет температуры нагрева
Стальной резец массой $2 space кг$ был нагрет до температуры $800 degree C$ и затем опущен в сосуд, содержащий $15 space л$ воды при температуре $10 degree C$. До какой температуры нагреется вода в сосуде?
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “р” для обозначения величин, связанных со стальным резцом.
Дано:
$V_в = 15 space л$
$m_р = 2 space кг$
$t_{р1} = 800 degree C$
$c_р = 500 frac{Дж}{кг cdot degree C}$
$rho_в = 1000 frac{кг}{м^3}$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$t_{в1} = 10 degree C$
СИ:
$V_в = 15 cdot 10^3 м^3$
$t_{в2} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Когда нагретый резец опускают в холодную воду, между этими двумя телами происходит теплообмен. Резец остывает и выделяет энергию, а вода получает эту энергию и нагревается. Соответственно, количество теплоты, которое выделится при остывании стального резца, численно будет равно количеству теплоту, которое получит вода.
Когда теплообмен завершится,температуры стального резца и воды будут одинаковы: $t_{в2} = t_{р2} = t_2$.
Запишем формулу для расчета количества теплоты, которое выделится при остывании резца:
$Q_р = с_р m_р (t_2 — t_{р1})$.
Запишем формулу для расчета количества теплоты, которое получила вода:
$Q_в = с_в m_в (t_2 — t_{в1})$.
Приравняем правые части этих уравнений, не забыв про знак “минус”, которые указывает на выделение энергии при охлаждении тела:
$с_р m_р (t_2 — t_{р1}) = — с_в m_в (t_2 — t_{в1})$.
Раскроем скобки:
$с_р m_р t_2 — с_р m_р t_{р1} = — с_в m_в t_2 + с_в m_в t_{в1}$.
Перенесем множители с $t_2$ на одну сторону уравнения и выразим эту температуру, до которой нагреется вода:
$с_р m_р t_2 + с_в m_в t_2 = с_в m_в t_{в1} + с_р m_р t_{р1}$,
$t_2 (с_р m_р + с_в m_в) = с_в m_в t_{в1} + с_р m_р t_{р1}$,
$t_2 = frac{с_в m_в t_{в1} + с_р m_р t_{р1}}{с_р m_р + с_в m_в}$.
Нам неизвестна масса воды, но известны ее плотность и объем. Выразим и рассчитаем массу через эти величины:
$m_в = rho_в V_в = 1000 frac{кг}{м^3} cdot 15 cdot 10^3 м^3 = 15 space кг$.
Теперь мы можем рассчитать температуру $t_2$:
$t_2 = frac{4200 frac{Дж}{кг cdot degree C} cdot 15 space кг cdot 10 degree C + 500 frac{Дж}{кг cdot degree C} cdot 2 space кг cdot 800 degree C}{500 frac{Дж}{кг cdot degree C} cdot 2 space кг + 4200 frac{Дж}{кг cdot degree C} cdot 15 space кг} = frac{630 cdot 10^3 space Дж + 800 cdot 10^3 space Дж}{1 cdot 10^3 frac{Дж}{degree C} + 63 cdot 10^3 frac{Дж}{degree C}} = frac{1430 cdot 10^3 space Дж}{64 cdot 10^3 frac{Дж}{degree C}} approx 22.3 degree C$.
Ответ: $t_2 approx 22.3 degree C$.
Какой температуры получится вода, если смешать $0.02 space кг$ воды при $15 degree C$, $0.03 space кг$ воды при $25 degree C$ и $0.01 space кг$ воды при $60 degree C$?
Дано:
$m_1 = 0.02 space кг$
$t_1 = 15 degree C$
$m_2 = 0.03 space кг$
$t_2 = 25 degree C$
$m_3 = 0.01 space кг$
$t_3 = 60 degree C$
$t — ?$
Посмотреть решение и ответ
Скрыть
Решение:
При смешивании жидкостей разных температур, мы знаем, что внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Для смешивания двух жидкостей мы можем записать, что $Q_1 = — Q_2$ или $Q_1 + Q_2 = 0$.
Сначала рассмотрим смешивание первых двух порций воды. Первая порция с температурой $15 degree C$ будет нагреваться (получать энергию), а вторая порция с температурой $25 degree C$ будет охлаждаться (выделять энергию). Эти энергии будут численно равны друг другу, но противоположны по знаку:
$cm_1(t_{1+2} — t_1) = — cm_2(t_{1+2} — t_2)$.
Найдем конечную температуру этой смеси:
$m_1(t_{1+2} — t_1) = — m_2 (t_{1+2} — t_2)$,
$m_1 t_{1+2} — m_1 t_1 = -m_2 t_{1+2} + m_2 t_2$,
$t_{1+2} (m_1 + m_2) = m_1 t_1 + m_2 t_2$,
$t_{1+2} = frac{m_1 t_1 + m_2 t_2}{m_1 + m_2} = frac{0.02 space кг cdot 15 degree C + 0.03 space кг cdot 25 degree }{0.02 space кг + 0.03 space кг} = frac{0.3 space кг cdot degree + 0.75 space кг cdot degree C}{0.05 space кг} = 21 degree C$.
Так мы получили смесь первой и второй порций воды массой $m_{1+2} = 0.05 space кг$ и температурой $t_{1+2} = 21 degree C$.
Теперь добавим третью порцию воды в полученную смесь. Смесь будет нагреваться (получать энергию), а третья порция воды будет охлаждаться (выделять энергию):
$Q_{1+2} = — Q_3$.
$cm_{1+2} (t — t_{1+2}) = — cm_3 (t — t_3)$,
$m_{1+2} (t — t_{1+2}) = — m_3 (t — t_3)$.
Выразим отсюда конечную температуру смеси из трех порций воды $t$:
$m_{1+2} t — m_{1+2} t_{1+2} = -m_3 t + m_3 t_3$,
$t (m_{1+2} + m_3) = m_{1+2} t_{1+2} + m_3 t_3$,
$t = frac{m_{1+2} t_{1+2} + m_3 t_3}{m_{1+2} + m_3}$.
Рассчитаем ее:
$t = frac{0.05 space кг cdot 21 degree C + 0.01 space кг cdot 60 degree}{0.05 space кг + 0.01 space кг} = frac{1.05 space кг cdot degree C + 0.6 space кг cdot degree C}{0.06 space кг} = 27.5 degree C$.
Ответ: $t = 27.5 degree C$.
Задача №9 на расчет количества теплоты, рассеиваемого в окружающую среду
Электрочайник с водой нагревается от температуры $70 degree C$ до температуры $80 degree C$ за $3 space мин$, а остывает от температуры $80 degree C$ до температуры $70 degree C$ за $9 space мин$. Какая часть количества теплоты, выделяемой спиралью чайника при нагревании воды, рассеивается в окружающую среду? Тепловые потери считать постоянными.
Внесем необходимые пояснения. Спираль чайника передает воде определенное количество теплоты $Q_2$. Часть ее ($Q_1$) рассеивается в окружающую среду. Т.е., количество теплоты $Q_2$, выделяемое спиралью, больше количества теплоты $Q$, необходимого для нагрева воды.
Дано:
$t_1 = 70 degree C$
$t_2 = 80 degree C$
$T_1 = 3 space мин$
$T_2 = 9 space мин$
$frac{Q_1}{Q_2} — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем количество теплоты, которое необходимо сообщить воде в чайнике, чтобы ее температура увеличилась с $70 degree C$ до $80 degree C$:
$Q = cm(t_2 — t_1)$.
Масса воды в чайнике нам неизвестна, поэтому примем ее, равной $1 space кг$. Тогда,
$Q = 4200 frac{Дж}{кг cdot degree C} cdot 1 space кг cdot (80 degree C — 70 degree C) = 42 space 000 space Дж = 42 space кДж$.
Когда вода в чайнике остывает с температуры $80 degree C$ до температуры $70 degree C$, она выделяет в окружающую среду точно такое же количество энергии $Q$. Остывание происходит за $9 space мин$. Значит, количество теплоты, которое выделяется в окружающую среду за $1 space мин$ будет равно:
$Q_0 = frac{42 space кДж}{9 space мин} approx 4.7 frac{кДж}{мин}$.
В условиях задачи сказано, что тепловые потери постоянны. Это означает, что вода массой $1 space кг$ отдает $4.7 space кДж$ каждую минуту, в том числе, и при ее нагревании.
Нагревается вода за 3 минуты. За это время она отдает в окружающую среду следующее количество теплоты:
$Q_1 = 4.7 space кДж cdot 3 = 14.1 space кДж$.
Тем не менее, чайник нагрел воду до нужной температуры. Значит, он сообщил воде количество энергии, равное $Q_2 = Q + Q_1$.
$Q_2 = 42 space кДж + 14.1 space кДж = 56.1 space кДж$.
Теперь мы можем рассчитать отношение $frac{Q_1}{Q_2}$, и узнать какая часть теплоты, выделяемая спиралью чайника, рассеивается в окружающую среду:
$frac{Q_1}{Q_2} = frac{14.1 space кДж}{56.1 space кДж} approx 0.25$.
Т.е., в окружающую среду рассеивается $frac{1}{4}$ часть энергии, сообщаемая воде в чайнике.
Можно доказать, что это соотношение останется постоянным для воды любой массы в этой задаче. Чем больше будет масса воды, тем больше энергии ей будет нужно, чтобы нагреться до определенной температуры. Больше будут и тепловые потери. Искомое соотношение же останется неизменным.
Ответ: $frac{Q_1}{Q_2} approx 0.25$.
Алгоритм 8
Расчеты по термохимическим уравнениям. Вычисление массы вещества по известному количеству теплоты
Пример. По термохимическому уравнению
С + О2 = СО2 + 412 кДж вычислите массу сгоревшего угля, если количество теплоты, выделившееся в результате реакции, составляет 82,4 кДж.
С помощью соответствующих обозначений запишем условие задачи, найдем молярную массу вещества, о котором идет речь в условии задачи
Дано:
Q = 82,4 кДж
Qр-ции = 412кДж
——————
m(С) = ? г
М(С) = 12 г/моль
Запишем термохимическое уравнение реакции. Обозначим вопросительным знаком количество вещества, массу которого надо
найти, и надпишем количество теплоты, записанное в условии задачи. Под формулой вещества обозначим молярное соотношение, вытекающее из уравнения реакции. Вычислим количество вещества, массу которого требуется найти.
Решение:
?моль 82,4 кДж
С + О2 = СО2 + 412 кДж
1 моль
Для этого составим пропорцию
х/1=82,4/412, откуда х= 0,2.
Следовательно, n(С)=0,2 моль
Перейдем от количества вещества к массе вещества. Для этого используем молярную массу вещества
m=n•М
m(С)=n(C)•М(С)
m(C)=0,2моль•12г/моль=2,4
Запишем ответ
Ответ: m(С) = 2,4 г
Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
Название величины |
Обозначение |
Единица измерения |
Формула |
Масса |
m |
кг |
|
Температура |
t |
°С |
|
Удельная теплоемкость |
c |
Дж/кг•°С |
|
Количество теплоты |
Q |
Дж |
|
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.
Задача № 2.
Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.
Задача № 3.
Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?
Задача № 4.
В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь
Задача № 5.
На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?
Задача № 6.
По графику определите удельную теплоёмкость образца, если его масса 50 г.
Задача № 7.
Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?
Задача № 8.
Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
Задача № 9.
Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?
Задача № 10.
Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?
Задача № 11.
а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)
Задача № 12.
ОГЭ
Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).
Задача № 13.
В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.
Ответ: 39 °С.
Задача № 14. (повышенной сложности)
Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)
Дано: R = 0,05 м; t1 = 500 ˚С; t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,
Найти: h – ?
Краткая теория для решения Задачи на количество теплоты.
Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».
Как найти массу по термохимическому уравнению
Алгоритм 8
Расчеты по термохимическим уравнениям. Вычисление массы вещества по известному количеству теплоты
Пример. По термохимическому уравнению
С + О2 = СО2 + 412 кДж вычислите массу сгоревшего угля, если количество теплоты, выделившееся в результате реакции, составляет 82,4 кДж.
С помощью соответствующих обозначений запишем условие задачи, найдем молярную массу вещества, о котором идет речь в условии задачи
Запишем термохимическое уравнение реакции. Обозначим вопросительным знаком количество вещества, массу которого надо
найти, и надпишем количество теплоты, записанное в условии задачи. Под формулой вещества обозначим молярное соотношение, вытекающее из уравнения реакции. Вычислим количество вещества, массу которого требуется найти.
Решение:
Для этого составим пропорцию
х/1=82,4/412, откуда х= 0,2.
Следовательно, n(С)=0,2 моль
Перейдем от количества вещества к массе вещества. Для этого используем молярную массу вещества
химэко
Меню сайта
Категории каталога
| 8 класс [27] |
| 9 класс [16] |
| 10 класс [30] |
| 11 класс [5] |
| Экзамен [4] |
| Лаборатория [7] |
| Опорные конспекты [0] |
| Переменка [6] |
| НОТ школьника [9] |
| Решение задач [9] |
| Творческие работы учащихся [3] |
| Учебные пособия [5] |
Форма входа
Приветствую Вас Гость!
Поиск
Друзья сайта
Наш опрос
Статистика
Термохимические уравнения включают в себя кроме химических формул тепловой эффект реакции. Числовое значение в уравнении реакции строго соответствует количествам веществ, участников реакции, т.е. коэффициентам. Благодаря этому соответствию, можно установить пропорциональные отношения между количеством вещества или массой и количеством теплоты в этой реакции.
Например: Термохимическое уравнение разложения малахита
Мы видим, что на разложение 1 моля малахита необходимо израсходовать 47 кДж, при этом образуется 2 моля оксида меди, 1 моль воды и 1 моль углекислого газа. Если мы затратим энергии в 2 раза больше, мы сумеем разложить 2 моля малахита, при этом получим 4 моля оксида меди, 2 моля воды и 2 моля углекислого газа.
Аналогично можно установить пропорциональные отношения, используя коэффициенты и молярные массы участников реакции. 47 кДж энергии затратится на разложение 94 г малахита, при этом выделится 160 г оксида меди, 18 г воды и 44 г углекислого газа. Пропорция несложная, но, используя массовые числа, учащиеся часто допускают расчетные ошибки, поэтому я рекомендую решать задачи с пропорциями через количество вещества.
Задача 1. Определите количество теплоты, которое выделится при образовании 120 г MgO в результате реакции горения магния, с помощью термохимического уравнения.
2 Mq + O 2 = 2 MqO + 1204 кДж
1) Определяем количества оксида магния, используя формулу для нахождения количества вещества через массу.
n ( MqO ) = 120г/ 40 г/моль = 3 моль
2) Составляем пропорцию с учетом коэффициентов в уравнении реакции
Расчёты по термохимическим уравнениям
Теоретический материал представлен на страницах:
Любая химическая реакция сопровождается поглощением или выделением энергии. Термохимические уравнения показывают соотношение между кол-вом веществ, вступающих в реакцию, и кол-вом энергии, которую выделяют, либо поглощают эти вещества в процессе химической реакции.
Главное отличие термохимического уравнения от молекулярного заключается в том, что кроме формул и коэффициентов, в нем указывается еще и кол-во энергии (теплоты реакции), относящееся к числу молей реагирующих веществ, соответствующему коэффициентам в уравнении реакции.
Теплота реакции (тепловой эффект) обозначается буквой Q (измеряется в кДж), и записывается в конце уравнения. Знак «плюс» перед числом обозначает выделившееся кол-во энергии, знак «минус» — кол-во поглощенной энергии.
Реакции, протекающие с выделением энергии, называются экзотермическими; с поглощением энергии — эндотермическими.
Если известна масса одного из двух реагирующих веществ, на основе термохимического уравнения можно определить кол-во теплоты реакции.
Пример 1 . Определить теплоту реакции горения 320 г серы.
- Согласно уравнения реакции, при сгорании 1 моля серы выделяется 297 кДж энергии, нам надо узнать, сколько энергии выделится при сгорании 320 г серы.
- Для решения задачи необходимо составить и решить простую пропорцию:
- Переходим от молей к граммам:
- В пропорции заменяем моли на граммы:
Если известно кол-во выделенной (поглощенной) теплоты в ходе реакции, можно определить массы прореагировавших веществ.
Пример 2 . Определить кол-во сгоревшего угля, если в ходе горения было выделено 33520 кДж энергии.
- Согласно уравнения реакции, при сгорании 1 моль углерода (масса 1 моль С = 12 г) выделилсь 402,24 кДж энергии.
- Составляем и решаем пропорцию:
Пример 3 . При горении 1 л метана (н.у) выделяется 39 кДж энергии. Составить термохимическое уравнение реакции и вычислить тепловой эффект.
Пример 4 . При горении 2,4 г магния (н.у) выделяется 60,12 кДж энергии. Составить термохимическое уравнение реакции.
Пример 5 . Два моля аммиака образуются в результате взаимодействия 1 моля азота с тремя молями водорода. Необходимо составить уравнение термохимической реакции, в ходе которой выделяется 92 кДж тепла, а все вещества, участвующие в реакции, являются газами.
Это очень простая задача, решение которой указано в условии.
Второй вариант записи термохимического уравнения.
Пример 6 . Составить термохимическое уравнение эндотермической реакции образования двухвалентного оксида азота из азота и кислорода с поглощением 180 кДж энергии. Записать это уравнение для образования 1 моля NO.
Первая часть задания не вызывает трудностей:
В этом термохимическом уравнении 2 моля оксида азота образуется при взаимодействии 1 моля азота и 1 моля кислорода. Для того, чтобы переписать данное уравнение для 1 моля оксида азота, необходимо все коэффициенты и кол-во теплоты разделить на 2:
Пример 7 . При образовании 50 г карбоната кальция (CaCO3) выделилось 80 кДж энергии. Определить тепловой эффект реакции разложения одного моля карбоната кальция.
- Определяем кол-во энергии, выделяемое при образовании 1 моля CaCO3 (М(CaCO3)=100 г/моль):
- Термохимическое уравнение реакции образования 1 моль карбоната кальция имеет вид:
- Термохимическое уравнение реакции разложения 1 моль карбоната кальция имеет вид:
- Q=-160 кДж
Пример 8 . Рассчитать кол-во выделенной энергии при образовании 2 л аммиака при н.у.
- Согласно термохимического уравнения — 1 моль аммиака образовался из полумоля азота и полутора молей водорода. Составляем пропорцию:
Пример 9 . Рассчитать тепловой эффект реакции:
- На основании первого следствия из закона Гесса:
- Теплоты образования простых веществ равны нулю:
- Теплоты образования сложных веществ берем из таблицы:
- Подставляем числовые значения в уравнение:
- Термохимическое уравнение реакции будет иметь вид:
Пример 10 . Рассчитать тепловой эффект реакции:
- Тепловой эффект реакции будем рассчитывать по формуле, вытекающей из второго следствия закона Гесса:
- Тепловые эффекты сгорания C2H4 и C2H6 можно взять из приведенных выше термохимический уравнений.
- Тепловой эффект сгорания водорода можно вычислить из термохимического уравнения образования 1 моля воды (теплоту образования воды берем из таблицы):
- Подставляем численные значения в формулу:
- Термохимическое уравнение реакции будет иметь вид:
Пример 11 . Определить скорость изменения реакции синтеза аммиака при а) увеличении концентрации исходных веществ в 2 раза; б) уменьшении давления в реакционной смеси в 2 раза:
- Записываем кинетическое уравнение данной реакции:
- Если концентрации исходных веществ будут увеличены в 2 раза, кинетическое уравнение примет вид:
- Составляем отношение и решаем его:
- Увеличение концентрации исходных веществ в 2 раза приведет к ускорению скорости реакции в 16 раз.
- Исходя из того факта, что концентрации газов пропорциональны давлению (при уменьшении давления в 2 раза концентрации также уменьшатся в 2 раза), логично предположить, что при снижении в 2 раза давления скорость протекания реакции снизится в 16 раз. Убедимся в этом, составив соотношение кинетических уравнений.
- Исхдное кинетическое уравнение:
- Для удобства чтения формул сделаем подстановку:
- Кинетическое уравнение при снижении давления в 2 раза:
- Соотошение:
- При уменьшении давления в реакционной смеси в 2 раза скорость протекания реакции уменьшится в 16 раз.
Пример 12 . Определить скорость изменения реакции с температурным коэффициентом 4 (γ=4) при повышении температуры с 10°C до 30°C.
Для решения задачи воспользуемся правилом Вант-Гоффа, которое выражается следующей математической формулой:
Все, что нам нужно сделать — подставить численные значения в формулу и провести расчеты:
При повышении температуры с 10 до 30 градусов Цельсия скорость реакции увеличится в 16 раз.
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
источники:
http://himekoscho.ucoz.ru/load/termokhimicheskie_uravnenija/27-1-0-130
http://prosto-o-slognom.ru/chimia_primery/005-termochimicheskie_uravneniya.html
На практике часто приходится проводить различные тепловые расчёты. Для увеличения эргономичности тепловой системы жилых домов измеряют количество тепловой энергии, рассеиваемой через вентиляцию, окна, расщелины.
Для расчёта количества тепловой энергии нужно измерить массу (m), разность температуры в начале и в конце процесса
Δt=tкон−tнач
, а также знать теплоёмкость (c) данного вещества.
Чтобы нагреть некоторое вещество массой (1) кг на (1°C), необходимо затратить количество теплоты, равное удельной теплоёмкости (c) данного вещества.
Количество теплоты, получаемое веществом при нагревании, прямо пропорционально удельной теплоёмкости вещества, его массе и разности температур, то есть:
Q=cmΔt
или
Данная формула даёт возможность найти и выделяемую при охлаждении вещества теплоту.
Чтобы рассчитать количество теплоты, необходимое для нагревания вещества (или выделяемое им при охлаждении), следует удельную теплоёмкость вещества умножить на его массу и на разность между конечной и начальной температурой вещества.
Так как конечная температура остывающего вещества меньше его начальной температуры:
то изменение температуры оказывается отрицательным числом:
Значит, и выделяемое веществом количество теплоты выражается отрицательным числом:
Последний факт обозначает не рост, а убыль внутренней энергии вещества.