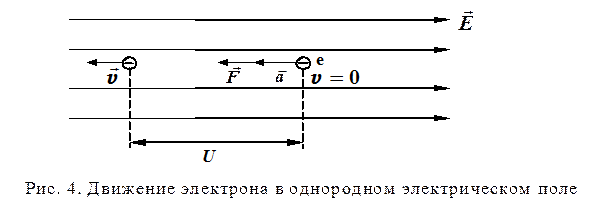Как найти массу заряда физика

В рамках физики и химии 100 лет как доказано, что материя состоит из электронов, протонов и нейтронов. Эксперименты демонстируют, что свободные нейтроны за 614 сек наполовину распадаются на электроны и протоны. Инерциальные свойства электронов протонов и нейтронов определяются методом масс — спектрометрии. Масс-спектрометр — прибор для определения масс заряженных частиц и массы атомов (молекул) по характеру движения их ионов в электрическом и магнитном полях.

Массу нейтрального атома нельзя измерить традиционной масс-спектрометрией. Однако, если отнять у него или добавить ему один и более электронов, то он превратится в йон, характер движения которого в этих полях будет определяться его массой и электрическим зарядом. Строго говоря, в масс-спектрометрах определяется не масса, а отношение массы к электрическому заряду. Если заряд известен, то однозначно определяется масса иона, а значит, можно вычислить массу нейтрального атома и его ядра. Конструктивно масс-спектрометры могут сильно отличаться друг от друга. В них могут использоваться как статичные поля, так и изменяющиеся во времени поля, магнитные и/или электрические.

Рассмотрим один из наиболее простых вариантов определения массы частицы.

Масс-спектрометр состоит из следующих основных частей:

Из ионного источника 1 ускоренные ионы через щель 2 попадают в область 3 постоянного и однородного электрического и магнитного полей. Направление электрического поля задаётся положением пластин конденсатора и показано стрелками. Магнитное поле направлено перпендикулярно плоскости рисунка.

В области 3 электрическое и магнитное поле отклоняют ионы в противоположные стороны и величины напряжённостей этих полей Е и Н₁ подобраны так, чтобы силы их действия на ионы (соответственно qЕ и qvН₁, где q — заряд, а v — скорость иона) компенсировали друг друга, т.е. было qЕ = qvН₁. Создается монохроматичный пучок ионов. При скорости иона v = Е/Н₁ он движется не отклоняясь в области 3 и проходит через вторую щель 4, попадая в область 5 однородного и постоянного магнитного поля напряжённостью Н₂. В этом поле ион движется по окружности 6, радиус R которой определяется из соотношения mv 2 /R = qvH₂, где m — масса иона. Так как v = Е/Н₁, масса частицы определяется из соотношения

Таким образом, при известном заряде иона его масса определяется радиусом R круговой орбиты в области 5.

Схема масс-спектрометра:

1. — ионный источник,
2. — щелеваяе диафрагма,
3. — область однородных и постоянных электрического и магнитного полей (силовые линии электрического поля направлены вдоль плоскости рисунка м показаны стрелками, область магнитного поля показана штриховкой, его силовые линии перпендикулярны плоскости рисунка),
4. — щелевая диафрагма
5. — область однородного и постоянного магнитного поля (силовые линии перпендикулярны плоскости рисунка),
6. — траектория иона,
7. — детектор.

Если в качестве детектора ионов (7) использовать фотопластинку, то этот радиус с высокой точностью покажет чёрную точку в том месте проявленной фотопластинки, куда попадал пучок ионов. В современных масс-спектрометрах в качестве детекторов обычно используют электронные умножители или микроканальные пластинки. Масс-спектрометр позволяет определять массы с очень высокой относительной точностью Δm/m = 10 -8 — 10 -7 .

Анализ масс-спектрометром смеси атомов различной массы позволяет также определить их относительное содержание в этой смеси. В частности, может быть установлено содержание различных изотопов какого-либо химического элемента.

Согласно принятой обработке эксперимента инерциальные силы полностью обусловлены инерциальными свойствами ньютоновской массы (m) — нейтральной, не несущей заряда материи. Однако, в эксперименте все анализируемые частицы несут заряды. Заряды, согласно электродинамике, обладают инерциальными свойствами без относительно к механической массе.

Cила Лоренца вызывает изменение магнитного поля, изменение которого, в свою очередь, вызывает появление ЭДС пропорциональной скорости изменения магнитного потока (ускорению).

ε_i= ∫ E_bdl = — — L dt

где dФ/dt -скорость изменения магнитного поля. Сопротивление изменению скорости и есть проявление инерции.

В тоже время при обработке результатов эксперимента инерциальные свойства, обусловленные наличием заряда, совершенно не учитываются. В 2012 году масс — спектроскопии исполнится 100 лет, но до настоящего времени не появилось ни одной работы, содержащей критические замечания, касающиеся обработки результатов эксперимента и, соответственно, ответов на следующий вопрос:

Почему не учитываются инерциальные свойства электрического заряда иона?

Соответственно, мы считаем необходимым предложить альтернативные варианты обработки экспериментальных данных, полученных в результате масс — спектроскопии микрочастиц.

Целью данной работы является изучение движения элементарных частиц в электрическом и магнитном полях, экспериментальное определение удельного заряда электрона с помощью магнетрона.

Электрон является носителем элементарного отрицательного заряда е (e = –1,6∙10 —19 Кл). Отношение его заряда к массе e/m называется удельным зарядом электрона. Удельный заряд может быть экспериментально определён различными методами. Все они основаны на поведении электрона в электрическом и магнитном полях.

В электрическом поле напряжённостью (рис .4) на электрон действует сила

, (2.9.1)

которая сообщает электрону ускорение и направлена против поля.

Под действием этой силы электрон, пройдя расстояние между точками с разностью потенциалов U, приобретает кинетическую энергию

. (2.9.2)

Движение электрона в однородном магнитном поле происходит под действием силы Лоренца

, (2.9.3)

где — вектор скорости электрона; — вектор индукции магнитного поля; е – заряд электрона.

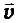
Сила Лоренца перпендикулярна как скорости электрона, так и направлению магнитного поля. Она не меняет модуля скорости и кинетической энергии частицы.

Модуль силы Лоренца

, (2.9.4)

где a — угол между векторами и .

Сила Лоренца сообщает электрону нормальное (центростремительное) ускорение и вызывает движение его по окружности радиуса R, если угол a составляет 90 o (рис. 5). Таким образом, по второму закону Ньютона:

, (2.9.5)

откуда радиус окружности

. (2.9.6)

Из формулы (2.9.6) видно, что радиус окружности зависит от удельного заряда e/m. Этот факт и положен в основу метода определения удельного заряда с помощью магнетрона.

Магнетрон представляет собой высоковакуумную элек­тронную трубку, имеющую пря­мую металлическую нить (ка­тод), расположенную по оси ци­линдрического анода.

Для нашей работы магнетрон с успехом можно заменить обычной электронной лампой с цилиндрическим анодом, на оси которого расположен катод (рис. 6, а). Лампа помещается внутри длинного соленоида, при помощи которого параллельно оси создаётся магнитное поле напряжённостью .

Катод нагревается электрическим током и испускает электроны, которые под действием электрического поля движутся к аноду. Когда магнитное поле отсутствует, электроны движутся по радиу

сам цилиндрического анода (рис. 6 б, линия 1).

Если включить магнитное поле, траектория движения искривляется, и тем больше, чем сильнее поле (рис. 6, б, линия 2). Все электроны достигают анода, и величина анодного тока в цепи практически не изменяется до определённого момента, когда при дальнейшем увеличении магнитного поля радиус траектории всё больше уменьшается и при некотором критическом значении В_кр, электроны, не достигнув анода, вернутся обратно к катоду (рис. 6, б, линия 3).

При выполнении условия В > В_кр электроны уже не будут попадать на анод, и ток станет равен нулю (рис. 6, б, линия 4).

На рис. 7 приведен график зависимости анодного тока I_А от ин­дукции магнитного поля при некотором анод­ном напряжении U_А (сбросовая характе­ристика магнетрона).

Если бы все электроны, вылетающие из катода, имели одну и ту же скорость, анодный ток I_А спадал бы до нуля точно при критическом значении В_кр индукции магнитного поля (рис. 7, штриховая линия). Однако скорости вылетевших электронов разные, поэтому уменьшение тока происходит на довольно протяжённом участке вблизи В_кр (рис. 7, сплошная линия).

Критическое значение индукции магнитного поля является некоторой функцией анодного напряжения U_А. Эту зависимость легко установить, если предположить, что скорость электрона при его движении в магнетроне остаётся постоянной по модулю. При В = В_кр, радиус окружности, по которой движется электрон, равен R_А /2, где R_А – радиус анода. Подставляя его в уравнение (2.9.6), получим:

. (2.9.7)

Решая совместно уравнения (2.9.2) и (2.9.7), получим формулу для расчёта удельного заряда электрона:

, (2.9.8)

где U_А — разность потенциалов между катодом и анодом.

Индукция магнитного поля в соленоиде может быть рассчитана по закону Био — Савара — Лапласа или по теореме о циркуляции индукции магнитного поля по замкнутому контуру

, (2.9.9)

где – длина соленоида; N – число витков соленоида; I_сол — сила тока, протекающего через соленоид (сила намагничивающего тока); – магнитная постоянная.

Критическому значению индукции магнитного поля В_кр соответствует критическое значение силы тока I_кр. Учитывая это и подставляя (2.9.7) в (2.9.8), получим

. (2.9.10)

При выводе (2.9.10) предполагалось, что электрическое и магнитное поля действуют на электрон по очереди, сначала он в электрическом поле разгоняется до скорости , а затем с этой постоянной скоростью движется в магнитном поле.

В рассматриваемом случае электрон движется в скрещенных магнитном и электрическом полях и одновременно испытывает действие сил со стороны обоих полей. Вследствие этого, скорость электрона не постоянна (она возрастает по мере приближения к аноду), а траектория его движения отличается от круговой. Данное обстоятельство позволяет утверждать, что формула (2.9.10) не точна. Тем не менее, как следует из результатов точного анализа рассматриваемой задачи, эта формула в целом удовлетворительно описывает физику процессов и с точностью до коэффициента пропорциональности является правильной.

Окончательная расчётная формула имеет вид:

, (2.9.11)

где = 0,1 м; N = 1000 витков; R_А = 5 мм; A – коэффициент, учитывающий отличие реальной траектории движения электрона в скрещенных электрическом и магнитном полях от окружности. Для нашей экспериментальной установки А=1,3.

Тщательные измерения удельного заряда и известное из опытов Милликена (1909 г.) значение величины заряда электрона позволили определить его массу и установить зависимость массы от скорости.

В принципе теми же методами определяются массы атомов и молекул. Соответствующие приборы для определения масс атомов и молекул (точнее, их ионов) носят название масс-спектрографов. Для примера можно рассмотреть принципиальное устройство одного из масс-спектрографов (рис. 8).

Сначала пучок ионов проходит через фильтр скоростей, в котором на движущиеся ионы одновременно действуют взаимно перпендикулярные электрическое и магнитное поля. Направления полей выбираются так, чтобы силы, действующие на ионы с их стороны, были противоположны по направлению. Через щель фильтра, противоположную входной, выхо­дят только те ионы, на которые действуют равные по величине силы и .

q∙E = q∙ ∙B. (2.9.12)

Следовательно, из фильтра вылетают ионы одинаковых скоростей

. (2.9.13)

При выходе из фильтра частицы попадают в магнитное поле, перпендикулярное их скорости. Траектория их движения — окружность, радиус которой зависит от удельного заряда частицы

. (2.9.14)

Попадая на фотопластинку, ионы оставляют след, расстояние которого от выходной щели фильтра зависит от удельного заряда ионов.

По найденным значениям q/m можно определить массы ионов.

В наши дни точность определения масс ионов с помощью масс-спектрографов достигают 6 —8 значащих цифр (правда, не в граммах, а по отношению к массе эталонного атома).

Масс-спектрографические методы позволяют проводить количественный анализ нефти, состоящий из молекул различных углеводородов, трудно различимых обычными химическими способами. При большой мощности ионного пучка этот метод позволяет разделять изотопы в заметных количествах.

Масс-спектрографический метод часто применяют для определения изотопного состава исследуемого вещества. В частности, он был применён при исследовании лунного грунта. Близость изотопного состава земных и лунных пород свидетельствует об одновозрастности и единстве происхождения земного и лунного вещества. По-видимому, это следует распространить и на другие космические тела солнечной системы. Исследования вещества метеоритов не противоречат такому обобщению.

Масс-спектрографы нашли широкое применение в различных областях физики, химии, техники. Они используются для определения содержания примесей в газах, для анализа состава и процентного содержания различных смесей углеводородов и т. д.

Необходимые приборы: лабораторный стенд, внутри которого смонтированы все элементы схемы; цифровой вольтметр (или осциллограф).

На рис. 9 приведена схема экспериментальной установки, которая технически реализована на лабораторном стенде с возможностью самостоятельно вручную и с управлением от внешних источников изменять параметры эксперимента.

Экспериментальная установка состоит из трёх цепей.

Цепь намагничивающей катушки состоит из соленоида, создающего однородное магнитное поле при подключении к нему источника постоянного тока ε₃, регулятора тока с внутренним и внешним управлением (коммутация осуществляется тумблером S₁) и низкоомного резистора R₅ =1 Ом, предназначенного для контроля силы тока I_сол в соленоиде по величине напряжения на этом сопротивлении.

Анодная цепь состоит из электронной лампы Л, источника постоянного тока ε₁, делителя напряжения на резисторах R₂, R₃, R₄ и последовательно включенного резистора R₁ = 1кОм, предназначенного для контроля силы тока в анодной цепи I_А, по величине напряжения на этом резисторе.

Цепь накала включает в себя нитевидный катод К лампы Л, источник тока ε₂ и тумблер S₂ , отключающий его.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10070 — | 7511 — или читать все.

Учащимся

Каким же образом можно экспериментально определить массу электрона или протона, ускоряя заряженную частицу на известном отрезке пути в известном однородном электрическом поле и измеряя ее конечную скорость? Как известно, если тело проходит путь d в направлении силы F, то работа Fd, затраченная на перемещение тела, равна приращению его кинетической энергии. Если же движение начинается от состояния покоя, то эта работа равна также конечной кинетической энергии тела: Fd= mv 2 /2

Таким образом, если известны F, d и v, то отсюда можно найти массу m.

В опытах, о которых пойдет речь, интересующие нас заряженные частицы ускоряются однородным силовым полем между двумя заряженными металлическими пластинами. Зная расстояние между пластинами и число заряжающих их батарей, можно определить электрическую силу, приложенную к каждому элементарному заряду. Опыты производятся в вакууме, чтобы исключить сопротивление воздуха, имевшее место в микро-микровесах. Кроме того, поскольку протоны и электроны более чем в 10 11 раз легче пластмассовых шариков, использованных в микро-микровесах, в данных опытах можно пренебречь силой тяготения по сравнению с электрическими силами.
Некоторое количество водорода подвергается ионизации вблизи пары заряженных пластин (рис.), после чего некоторые из ионов заходят с пренебрежимо малой скоростью через небольшое отверстие в пространство между пластинами. По мере движения ионов от одной пластины к другой электрическое поле ускоряет ионы, сообщая им конечную кинетическую энергию mv 2 /2. В правой пластине имеется небольшое отверстие, через которое некоторые из ионов могут попадать в камеру длиной 0,50 м (рис.). Эта камера изготовлена из проводящего материала, и, поскольку в ней нет электрического поля, ионы проходят всю ее длину без изменения своей скорости. На прохождение всего этого пути иону требуется всего лишь несколько микросекунд (1 мкс=10 -6 с). Хотя этот промежуток времени и очень мал, все же он доступен точному измерению посредством специального измерительного устройства. Это позволяет точно определить конечную скорость иона v.
Для измерения времени прохождения ионами длинной камеры от одного конца до другого надо заметить момент, когда данный ион покинет данную точку слева, и время, когда этот же ион достигнет дальнего конца справа. Чтобы заметить время, когда данный ион входит в длинную камеру, помещаем около входа пару небольших отклоняющих пластин (рис.). С их помощью можно управлять направлением пучка водородных ионов. Когда отклоняющие пластины заряжены, на ионы водорода действует боковая электрическая сила, которая отклоняет их в сторону от их траектории. Если же затем разрядить отклоняющие пластины, то по продольной оси камеры будут двигаться только те ионы, которые только что или позже попали в камеру; поэтому первыми ионами, прошедшими отверстие на дальнем конце, будут те, которые прошли весь путь в 0,50 м за время с момента разрядки пластин. Приход этих ионов регистрируется воспринимающим элементом, помещенным за отверстием.
Для измерения промежутка времени с момента разрядки пластин до момента прихода первых ионов на воспринимающий элемент отклоняющие пластины в камере соединяются с вертикальными отклоняющими пластинами осциллографа (рис.). Момент разряжения пластин в длинной камере отмечается пиком на кривой, вычерчиваемой на экране, осциллографа. Воспринимающий элемент у дальнего конца длинной камеры присоединяется к тем же вертикальным отклоняющим пластинам осциллографа (электрические соединения обоих концов камеры выполняются совершенно одинаково). Когда пучок ионов попадает в воспринимающий элемент, на экране осциллографа появляется второй пик (рис.). Два пика появляются в разных местах экрана, так как они возникли в разное время. В течение промежуточного времени между этими двумя моментами развертывающая цепь осциллографа вызывает горизонтальное перемещение электронного пучка на экране. Электронный пучок в осциллографе проходит расстояние между двумя пиками за то же время, за какое ионы водорода проходят 0,50 м в камере.

В современных осциллографах цепь развертки может вызвать горизонтальное перемещение электронного пучка на экране трубки от одного конца до другого за несколько сотых долей микросекунды. Для измерения скорости ионов цепь развертки настраивается так, чтобы вся кривая проходилась за 5 микросекунд. Тогда два пика на экране осциллографа будут заметно разделены. Измерением расстояния между пиками определяется время, за которое пучок пересекает длинную камеру. Находят промежуток времени от момента, когда пучок получает возможность двигаться прямо вперед, до момента, когда он попадает в воспринимающий элемент, с точностью до 0,01 микросекунды. В случае ионов водорода и 90- вольтовой батареи, создающей ускоряющую электрическую силу, время пролета равно 3,82 микросекунды. Отсюда можно вычислить скорость v ионов в длинной камере. Она равна 0,50 м/(3,82*10 -6 с) = = 1,31*10 5 м/с.
С другой стороны, пластины здесь ровно втрое дальше друг от друга, чем в микро-микровесах, в которых производился опыт Милликена,; кроме того, здесь используется втрое меньше таких же батарей. Поскольку сила, приходящаяся на элементарный заряд, пропорциональна числу одинаковых батарей и обратно пропорциональна расстоянию между пластинами, на каждый элементарный заряд теперь должна действовать в девять раз меньшая сила, т. е. 1/9*10 -14 ).
Если предположить, что один атом водорода несет один элементарный заряд, то каждый ион между пластинами испытывает только что выраженную силу. Двигаясь от одной пластины к другой, ион проходит путь 9,3 10 -3 м по направлению силы, так что произведенная работа по перемещению иона равна Fd = 1/9(1,4*10 -14 Н)*( 9,3 10 -3 м)= 1,4 10 -17 Дж. Следовательно,
mv/2=m (1,3*10 5 м/с) 2 /2=1,4 *10 -17 Дж.
Отсюда для массы иона водорода т находим
m= 1,7 *10 -27 кг.

Но ведь эта величина нам хорошо известна. В пределах точности наших измерений она совпадает с массой атома водорода.
Теперь можно подвести итог. Если ион водорода заряжен однократно, то его масса почти равна массе атома водорода. Можно даже сделать дальнейший шаг и утверждать, что ион водорода действительно является носителем единичного заряда и что его масса практически равна массе атома. Это должно быть правильным, так как предположение, что ион несет больший заряд, приведет к абсурдному результату. Например, если ион несет два элементарных заряда, то действительная величина mv 2 /2 должна быть в два раза больше принятого нами значения. Поскольку мы измеряли v, это может только значить, что масса иона в два раза больше найденной нами. Такой ион водорода обладал бы массой, в два раза превосходящей массу атома, осколком которого он является. Этот вывод настолько неправдоподобен, что мы его отбрасываем.

Ранее уже имелись указания, что электроны представляют собой строительные элементы, входящие во все атомы. По-видимому, ион водорода представляет собой атом водорода, потерявший один электрон. Кроме того, мы никогда ни в этом, ни в других опытах не встречали положительно заряженного осколка водорода с двумя положительными элементарными зарядами. Это одно из многих доказательств того, что положительно заряженный ион водорода является конечным строительным элементом. Это — протон. Когда водород расщепляется на заряженные частицы, то, как только что было установлено, протону принадлежит почти вся масса атома. Поэтому электроны должны быть очень легкими. Можно использовать те же приборы для измерения массы электрона и таким образом проверить этот вывод.

From Wikipedia, the free encyclopedia

Mass-to-charge ratio
Common symbols	m/Q
SI unit	kg/C
In SI base units	kg⋅A-1⋅s-1
Dimension

The mass-to-charge ratio (m/Q) is a physical quantity relating the mass (quantity of matter) and the electric charge of a given particle, expressed in units of kilograms per coulomb (kg/C). It is most widely used in the electrodynamics of charged particles, e.g. in electron optics and ion optics.

It appears in the scientific fields of electron microscopy, cathode ray tubes, accelerator physics, nuclear physics, Auger electron spectroscopy, cosmology and mass spectrometry.^[1] The importance of the mass-to-charge ratio, according to classical electrodynamics, is that two particles with the same mass-to-charge ratio move in the same path in a vacuum, when subjected to the same electric and magnetic fields.

Some disciplines use the charge-to-mass ratio (Q/m) instead, which is the multiplicative inverse of the mass-to-charge ratio. The CODATA recommended value for an electron is Q/m = −1.75882001076(53)×10¹¹ C⋅kg⁻¹.^[2]

Origin[edit]

When charged particles move in electric and magnetic fields the following two laws apply:

• Lorentz force law:

  

• Newton’s second law of motion:

  

where F is the force applied to the ion, m is the mass of the particle, a is the acceleration, Q is the electric charge, E is the electric field, and v × B is the cross product of the ion’s velocity and the magnetic flux density.

This differential equation is the classic equation of motion for charged particles. Together with the particle’s initial conditions, it completely determines the particle’s motion in space and time in terms of m/Q. Thus mass spectrometers could be thought of as «mass-to-charge spectrometers». When presenting data in a mass spectrum, it is common to use the dimensionless m/z, which denotes the dimensionless quantity formed by dividing the mass number of the ion by its charge number.^[1]

Combining the two previous equations yields:

This differential equation is the classic equation of motion of a charged particle in a vacuum. Together with the particle’s initial conditions, it determines the particle’s motion in space and time. It immediately reveals that two particles with the same m/Q ratio behave in the same way. This is why the mass-to-charge ratio is an important physical quantity in those scientific fields where charged particles interact with magnetic or electric fields.

Exceptions[edit]

There are non-classical effects that derive from quantum mechanics, such as the Stern–Gerlach effect that can diverge the path of ions of identical m/Q.

Symbols and units[edit]

The IUPAC recommended symbol for mass and charge are m and Q, respectively,^[3][4] however using a lowercase q for charge is also very common. Charge is a scalar property, meaning that it can be either positive (+) or negative (−). The Coulomb (C) is the SI unit of charge; however, other units can be used, such as expressing charge in terms of the elementary charge (e). The SI unit of the physical quantity m/Q is kilogram per coulomb.

Mass spectrometry and m/z[edit]

The units and notation above are used when dealing with the physics of mass spectrometry; however, the m/z notation is used for the independent variable in a mass spectrum.^[5] This notation eases data interpretation since it is numerically more related to the dalton.^[1] For example, if an ion carries one charge the m/z is numerically equivalent to the molecular or atomic mass of the ion in daltons (Da), where the numerical value of m/Q is abstruse. The m refers to the molecular or atomic mass number and z to the charge number of the ion; however, the quantity of m/z is dimensionless by definition.^[5] An ion with a mass of 100 Da (daltons) (m = 100) carrying two charges (z = 2) will be observed at m/z 50. However, the empirical observation m/z 50 is one equation with two unknowns and could have arisen from other ions, such as an ion of mass 50 Da carrying one charge. Thus, the m/z of an ion alone neither infers mass nor the number of charges. Additional information, such as the mass spacing between mass isotopomers or the relationship between multiple charge states, is required to assign the charge state and infer the mass of the ion from the m/z. This additional information is often but not always available. Thus, the m/z is primarily used to report an empirical observation in mass spectrometry. This observation may be used in conjunction with other lines of evidence to subsequently infer the physical attributes of the ion, such as mass and charge. On rare occasions, the thomson has been used as a unit of the x-axis of a mass spectrum.

History[edit]

In the 19th century, the mass-to-charge ratios of some ions were measured by electrochemical methods. In 1897, the mass-to-charge ratio of the electron was first measured by J. J. Thomson.^[6] By doing this, he showed that the electron was in fact a particle with a mass and a charge, and that its mass-to-charge ratio was much smaller than that of the hydrogen ion H⁺. In 1898, Wilhelm Wien separated ions (canal rays) according to their mass-to-charge ratio with an ion optical device with superimposed electric and magnetic fields (Wien filter). In 1901 Walter Kaufman measured the increase of electromagnetic mass of fast electrons (Kaufmann–Bucherer–Neumann experiments), or relativistic mass increase in modern terms. In 1913, Thomson measured the mass-to-charge ratio of ions with an instrument he called a parabola spectrograph.^[7] Today, an instrument that measures the mass-to-charge ratio of charged particles is called a mass spectrometer.

Charge-to-mass ratio[edit]

The charge-to-mass ratio (Q/m) of an object is, as its name implies, the charge of an object divided by the mass of the same object. This quantity is generally useful only for objects that may be treated as particles. For extended objects, total charge, charge density, total mass, and mass density are often more useful.

Derivation:

or

(1)

Since ,

or

(2)

Equations (1) and (2) yield

Significance[edit]

In some experiments, the charge-to-mass ratio is the only quantity that can be measured directly. Often, the charge can be inferred from theoretical considerations, so the charge-to-mass ratio provides a way to calculate the mass of a particle.

Often, the charge-to-mass ratio can be determined by observing the deflection of a charged particle in an external magnetic field. The cyclotron equation, combined with other information such as the kinetic energy of the particle, will give the charge-to-mass ratio. One application of this principle is the mass spectrometer. The same principle can be used to extract information in experiments involving the cloud chamber.

The ratio of electrostatic to gravitational forces between two particles will be proportional to the product of their charge-to-mass ratios. It turns out that gravitational forces are negligible on the subatomic level, due to the extremely small masses of subatomic particles.

Electron[edit]

The electron charge-to-mass quotient, , is a quantity that may be measured in experimental physics. It bears significance because the electron mass m_e is difficult to measure directly, and is instead derived from measurements of the elementary charge e and . It also has historical significance; the Q/m ratio of the electron was successfully calculated by J. J. Thomson in 1897—and more successfully by Dunnington, which involves the angular momentum and deflection due to a perpendicular magnetic field. Thomson’s measurement convinced him that cathode rays were particles, which were later identified as electrons, and he is generally credited with their discovery.

The CODATA recommended value is −e/m_e = −1.75882001076(53)×10¹¹ C⋅kg⁻¹.^[2] CODATA refers to this as the electron charge-to-mass quotient, but ratio is still commonly used.

There are two other common ways of measuring the charge-to-mass ratio of an electron, apart from Thomson and Dunnington’s methods.

1. The magnetron method: Using a GRD7 Valve (Ferranti valve),^{[dubious – discuss]} electrons are expelled from a hot tungsten-wire filament towards an anode. The electron is then deflected using a solenoid. From the current in the solenoid and the current in the Ferranti Valve, e/m can be calculated.^{[citation needed]}
2. Fine beam tube method: A heater heats a cathode, which emits electrons. The electrons are accelerated through a known potential, so the velocity of the electrons is known. The beam path can be seen when the electrons are accelerated through a helium (He) gas. The collisions between the electrons and the helium gas produce a visible trail. A pair of Helmholtz coils produces a uniform and measurable magnetic field at right angles to the electron beam. This magnetic field deflects the electron beam in a circular path. By measuring the accelerating potential (volts), the current (amps) to the Helmholtz coils, and the radius of the electron beam, e/m can be calculated.^[8]

Zeeman Effect[edit]

The charge-to-mass ratio of an electron may also be measured with the Zeeman effect, which gives rise to energy splittings in the presence of a magnetic field B:

Here m_j are quantum integer values ranging from −j to j, with j as the eigenvalue of the total angular momentum operator J, with^[2]

where S is the spin operator with eigenvalue s and L is the angular momentum operator with eigenvalue l. g_J is the Landé g-factor, calculated as

The shift in energy is also given in terms of frequency υ and wavelength λ as

Measurements of the Zeeman effect commonly involve the use of a Fabry–Pérot interferometer, with light from a source (placed in a magnetic field) being passed between two mirrors of the interferometer. If δD is the change in mirror separation required to bring the mth-order ring of wavelength λ + Δλ into coincidence with that of wavelength λ, and ΔD brings the (m + 1)th ring of wavelength λ into coincidence with the mth-order ring, then

It follows then that

Rearranging, it is possible to solve for the charge-to-mass ratio of an electron as

See also[edit]

• Gyromagnetic ratio
• Thomson (unit)

References[edit]

Bibliography[edit]

• Szilágyi, Miklós (1988). Electron and ion optics. New York: Plenum Press. ISBN 978-0-306-42717-6.
• Septier, Albert L. (1980). Applied charged particle optics. Boston: Academic Press. ISBN 978-0-12-014574-4.
• International vocabulary of basic and general terms in metrology =: Vocabulaire international des termes fondamentaux et généraux de métrologie. International Organization for Standardization. 1993. ISBN 978-92-67-01075-5.CC.
• IUPAP Red Book SUNAMCO 87-1 «Symbols, Units, Nomenclature and Fundamental Constants in Physics» (does not have an online version).
• Symbols Units and Nomenclature in Physics IUPAP-25 IUPAP-25, E.R. Cohen & P. Giacomo, Physics 146A (1987) 1–68.

External links[edit]

• BIPM SI brochure
• AIP style manual
• NIST on units and manuscript check list
• Physics Today’s instructions on quantities and units

ответы

ваш ответ

похожие темы

похожие вопросы 5

Модель атома можно представить себе следующим образом:

Рис. (2). Модель атома

Информация об этих частицах дана в таблице.

Рис. (3). Состав атома

Количество нейтронов в атомах может быть отлично от количества протонов и электронов.
Атом, потерявший один или несколько электронов, не будет нейтральным, а будет иметь заряд  «+». Его называют положительным ионом.

Атом, к которому присоединился электрон, приобретает заряд «-» и становится отрицательным ионом.

Узнать, сколько тех или иных частиц содержит нейтральный атом, поможет периодическая система химических элементов (таблица Менделеева). Любой элемент в таблице имеет порядковый номер и относительную атомную массу.

Рис. (7). Обозначение элемента в периодической таблице

Зная строение атома, можно объяснить электризацию тел.

Зная строение атома, можно объяснить существование проводников и диэлектриков.

Так, в металлах это — электроны, в растворах солей, кислот, щелочей — положительные и отрицательные ионы. Например, когда прикасаются металлической проволокой к отрицательно заряженному электрометру, свободные электроны передвигаются по проволоке, а электрометр разряжается.

Поэтому прикосновение деревянной линейки к заряженному электрометру не вызывает никаких изменений.
Зная строение атома, можно объяснить явление притяжения ненаэлектризованных тел к наэлектризованным.

Рис. (8). Воздействие положительно заряженной палочки на гильзу

В металлической гильзе есть свободные электроны. Под действием электрического поля палочки они приходят в движение, так как начинают притягиваться к ней. В результате происходит перераспределение заряда. Электроны скапливаются на стороне, которая ближе к палочке, и она заряжается отрицательно. На противоположной стороне недостаток электронов, поэтому она заряжается положительно. Но в целом заряд гильзы равен нулю (в соответствии с законом сохранения заряда).

Рис. (9). Распределение заряда при воздействии на нейтральную гильзу положительно заряженной палочки

Если палочка будет заряжена отрицательно, то свободные электроны будут отталкиваться от неё и перемещаться в противоположную сторону.

Рис. (10). Распределение заряда при воздействии на нейтральную гильзу отрицательно заряженной палочки

По такому же принципу происходит отклонение листочков незаряженного электроскопа при поднесении к нему (не касаясь) заряженной палочки.

Рис. (11). Распределение заряда на электроскопе

Электрическое поле палочки вызывает перераспределение зарядов в металлическом стержне электроскопа. В верхней части будет избыток электронов, а в нижней — недостаток. Поэтому оба листочка зарядятся положительно и оттолкнутся друг от друга.

Масса

В рамках физики и химии 100 лет как доказано, что материя состоит из электронов, протонов и нейтронов. Эксперименты демонстируют, что свободные  нейтроны за 614 сек наполовину распадаются на электроны и протоны. Инерциальные свойства электронов протонов и нейтронов определяются методом масс — спектрометрии. Масс-спектрометр — прибор для определения масс заряженных частиц и массы атомов (молекул) по характеру движения их ионов в электрическом и магнитном полях.

Массу нейтрального атома нельзя измерить традиционной масс-спектрометрией. Однако, если отнять у него или добавить ему один и более электронов, то он превратится в йон, характер движения которого в этих полях будет определяться его массой и электрическим зарядом. Строго говоря, в масс-спектрометрах определяется не масса, а отношение массы к электрическому заряду. Если заряд известен, то однозначно определяется масса иона, а значит, можно вычислить массу нейтрального атома и его ядра. Конструктивно масс-спектрометры могут сильно отличаться друг от друга. В них могут использоваться как статичные поля, так и изменяющиеся во времени поля, магнитные и/или электрические.

Рассмотрим один из наиболее простых вариантов определения массы частицы.

Масс-спектрометр состоит из следующих основных частей:  (1) ионного источника, где нейтральные атомы превращаются в ионы (например, под действием нагревания или СВЧ-поля) и ускоряются электрическим полем, (3) области постоянных электрических и магнитных полей, и (7) приёмника ионов, определяющего координаты точек, куда попадают ионы, пересекшие эти поля. Из ионного источника 1 ускоренные ионы через щель 2 попадают в область 3 постоянного и однородного электрического и магнитного полей. Направление электрического поля задаётся положением пластин конденсатора и показано стрелками. Магнитное поле направлено перпендикулярно плоскости рисунка. В области 3 электрическое и магнитное поле отклоняют ионы в противоположные стороны и величины напряжённостей этих полей Е и Н1 подобраны так, чтобы силы их действия на ионы (соответственно qЕ и qvН1, где q — заряд, а v — скорость иона) компенсировали друг друга, т.е. было qЕ = qvН1. Создается монохроматичный пучок ионов. При скорости иона v = Е/Н1 он движется не отклоняясь в области 3 и проходит через вторую щель 4, попадая в область 5 однородного и постоянного магнитного поля напряжённостью Н2. В этом поле ион движется по окружности 6, радиус R которой определяется из соотношения  mv2/R = qvH2,  где m — масса иона. Так как v = Е/Н1, масса частицы определяется из соотношения m = qH2R/v = qH1H2R/E.                                     [1] Таким образом, при известном заряде иона его масса определяется радиусом R круговой орбиты в области 5.

Схема масс-спектрометра: — ионный источник,  — щелеваяе диафрагма, — область однородных и постоянных электрического и магнитного полей (силовые линии электрического поля направлены вдоль плоскости рисунка м показаны стрелками, область магнитного поля показана штриховкой, его силовые линии перпендикулярны плоскости рисунка), — щелевая диафрагма — область однородного и постоянного магнитного поля (силовые линии перпендикулярны плоскости рисунка), — траектория иона, — детектор.

Если в качестве детектора ионов  (7) использовать фотопластинку, то этот радиус с высокой точностью покажет чёрную точку в том месте проявленной фотопластинки, куда попадал пучок ионов. В современных масс-спектрометрах в качестве детекторов обычно используют электронные умножители или микроканальные пластинки. Масс-спектрометр позволяет определять массы с очень высокой относительной точностью Δm/m = 10^-8 — 10^-7.

Анализ масс-спектрометром смеси атомов различной массы позволяет также определить их относительное содержание в этой смеси. В частности, может быть установлено содержание различных изотопов какого-либо химического элемента.

Согласно принятой обработке эксперимента инерциальные силы полностью обусловлены инерциальными свойствами ньютоновской массы (m) — нейтральной, не несущей заряда материи. Однако, в эксперименте все анализируемые частицы несут заряды. Заряды, согласно электродинамике, обладают инерциальными свойствами без относительно к механической массе.

Cила Лоренца вызывает изменение магнитного поля, изменение которого, в свою очередь, вызывает появление ЭДС пропорциональной скорости изменения магнитного потока (ускорению). 

			dФ
εi=	∫ Ebdl	= —	—
	L		dt

где dФ/dt -скорость изменения магнитного поля. Сопротивление изменению скорости и есть проявление инерции.

В тоже время при обработке результатов эксперимента инерциальные свойства, обусловленные наличием  заряда, совершенно не учитываются. В 2012 году масс — спектроскопии исполнится 100 лет, но  до настоящего времени не появилось ни одной работы, содержащей критические замечания, касающиеся обработки результатов эксперимента и, соответственно, ответов на следующий вопрос:

Почему не учитываются инерциальные свойства электрического заряда иона?

Соответственно, мы считаем необходимым предложить альтернативные варианты обработки экспериментальных данных, полученных в результате масс — спектроскопии микрочастиц. 

Феноменологическое доказательство>>