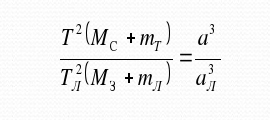Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.
Планеты солнечной системы
Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).
Содержание:
- 1 Рассчитываем массу Земли и Луны
- 2 Общие методики определения масс планет
- 3 Значения масс планет Солнечной системы
- 4 Определение масс звезд и галактик
Рассчитываем массу Земли и Луны
Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.
Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:
Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.
Земля и луна
Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.
Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.
Общие методики определения масс планет
Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –
Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.
В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.
Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.
Значения масс планет Солнечной системы
Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.
Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.
Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.
Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.
Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Определение масс звезд и галактик
Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.
Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.
Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:
Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.
Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.
Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.
Как определить массу Земли
Ньютон называл массой количество материи. Сейчас ее определяют как меру инертности тел: чем тяжелее предмет, тем труднее придать ему ускорение. Чтобы найти инертную массу тела, сравнивают давление, оказываемое им на поверхность опоры, с эталоном, вводят шкалу измерения. Для вычисления массы небесных тел используют гравиметрический метод.

Инструкция
Все тела, обладающие массой, возбуждают в окружающем пространстве гравитационные поля, подобно тому, как электрически заряженные частицы образуют вокруг себя электростатическое поле. Можно предположить, что тела несут в себе гравитационный заряд, аналогичный электрическому, или, по-другому, обладают гравитационной массой. С высокой точностью было установлено, что инертная и гравитационная массы совпадают.
Пусть имеется два точечных тела массами m1 и m2. Они удалены друг от друга на расстояние r. Тогда сила гравитационного притяжения между ними равна: F=C·m1·m2/r², где С – коэффициент, который зависит лишь от выбранных единиц измерения.
Если на поверхности Земли имеется небольшое тело, его размерами и массой можно пренебречь, т.к. габариты Земли намного превосходят их. При определении расстояния между планетой и поверхностным телом рассматривается только радиус Земли, т.к. высота расположения тела пренебрежимо мала в сравнении с ним. Получается, что Земля притягивает тело с силой F=M/R², где M – масса Земли, R – ее радиус.
Согласно закону всемирного тяготения, ускорение тел при действии силы тяжести на поверхности Земли равно: g=G•M/ R². Здесь G – гравитационная постоянная, численно равная примерно 6,6742•10^(−11).
Ускорение свободного падения g и радиус земли R находятся из непосредственных измерений. Константа G с большой точностью определена в опытах Кэвендиша и Йолли. Итак, масса Земли M=5,976•10^27 г ≈ 6•10^27 г.
Обратите внимание
Гравиметрический метод применим на данный момент только к Земле, поскольку в ходе его выполнения необходимо производить измерения, находясь на поверхности изучаемой планеты.
Полезный совет
Зная радиус Земли, легко найти ее объем. Он равен приблизительно 1121 млрд км³. Из объема и массы находится средняя плотность, по формуле ρ=M/V (ρ – плотность, M – масса, V – объем). Для Земли плотность составляет около 5,52 г/см³.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Планета – объект большой, его на весы не поставишь. Как же ученым удалось узнать массу Земли? Как измеряется масса далеких космических объектов?
Занимательная физика
Существует 2 способа определения массы Земли: с помощью барометра и математических вычислений, или анализа частиц нейтрино.
Барометр и законы Ньютона
Метод, применяемый с XVIII века. Для расчета используются второй закон Ньютона (F=mg) и закон всемирного тяготения (F=G*m*M/R^2).
F – это сила земного притяжения барометра, G – коэффициент гравитационной постоянной, R – радиус планеты, m – вес прибора, M – вес планеты.
Отдельно масса Земли вычисляется по формуле: M = g*R^2/G, где g – это ускорение свободного падения.
Ускорение свободного падения узнали, сбросив барометр с высокой башни и измерив время, которое он пролетел до столкновения с землей. Выяснилось, что за каждую последующую секунду барометр преодолевал почти 9.8 метров. Таким образом, g = 9.8 м/с².
Фотография Земли, сделанная 29 июля 2015 года с борта космического аппарата Deep Space Climate Observatory
Радиус Земли был известен еще с Античности. Столь сенсационное открытие сделал греческий математик Эратосфен в III веке до н.э.
Ученый подождал день летнего солнцестояния. В это время светило находится в самой высокой точке на небе и в 12 часов отбрасывает наименьшую тень в году.
Математик присмотрелся к обелиску, стоящему неподалеку, измерил отбрасываемую им тень, измерил сам обелиск, высчитал все углы, а потом сделал то же самое в соседнем городе. Расчеты дали ему окружность земли в 38.5 тысяч километров. Современные ученые пересчитали окружность подобным методом и высчитали 40 000 км.
Планета идеальным шаром не является, а потому ее радиус оказался 6371 км.
Труднее всего было найти коэффициент гравитационной постоянной. Для этого исследователи взяли однотонный свинцовый шар и посмотрели, с какой силой он притягивал барометр.
G = 6,67430(15)*10ˆ(-11) Н·м²·кг²
Подставив все эти цифры в уравнение, ученые высчитали, что Земля весит шесть септиллионов кг или 6^24 кг.
Нейтрино
Это мельчайшие субатомные частицы, которые испускает Солнце. Они проходят планету насквозь.
Испанские физики поставили лабораторию на Южном полюсе, дождались момента, когда Солнце окажется на Северном полюсе и выловили нейтрино с обратной стороны.
Эксперимент кажется фантастичным, однако измерив скорость частиц, прошедших сквозь Землю, физики нашли плотность планеты и, соответственно, массу.
Как измеряются далекие планеты?
Масса далеких планет вычисляется примерно. Основами для вычислений становятся орбиты планет, орбиты их спутников и гравитационные возмущения между ними.
Масса звезд вычисляется по степени их яркости. Считается, чем ярче небесное тело, тем оно массивнее. По светимости звезды определяется её химический состав, а значит примерная плотность и вес.
Начну с конца.
Математически, взяв за основу определённую систему аксиом, можно подтвердить что угодно. Например, что в пространстве невозможны прямые линии. Или на плоскости не может быть параллельных прямых. От слова «вообще». Или, наоборот, их может быть сколько угодно (в смысле — что через точку вне прямой можно провести сколько хотите прямых, не пересекающих данную). Мы просто получаем другую геометрию — геометрию многообразий, или геометрию Римана, или геометрию Лобачевского.
Вот с математическим доказательством «пустотелости Земли» тоже можно подобрать систему аксиом, из которых этот вывод следовал бы. Фигня вопрос. Беда лишь в том, что такой вывод противоречит ряду экспериментально подтверждённых фактов и некоторых интуитивных соображений.
Во-первых, модель пустотелой Земли не подтверждается сейсморазведкой. Землетрясения и мощные взрывы просвечивают Землю насквозь. Точнее, простукивают. Собственно, именно так и находят месторождения нефти и газа. И вот данные сейсморазведки, удивительное дело, никакой полости внутри Земли не показывают…
Во-вторых — генезис. Как образуются планеты — наука вполне отчётливо себе представляет: постепенное перераспределение пыли с образованием сначала более-менее компактных (по сравнению с первоначальным размером газопылевого облака) протопланет, затем их окончательное оформление в готовые планеты. Внимание, вопрос: как при вот таком процессе образования планет может получиться полое тело?
В-третьих — сопромат. Окей, допустим, что Земля — не сплошной шар, а пузырь. Не штука оценить потребную прочность стенок такого пузыря, учитывая, что он должен противостоять собственному весу своей оболочки. В принципе, такой расчёт по силам второкурснику, но, по счастью, его за меня уже сделали (см. «Наука и жизнь» №1 за 1970 год): по расчётам астрономов, прочность Земли выше, чем прочность стального шара того же размера с оболочкой толщиной 3000 км. Учитывая, что внутренность Земли по большей части находится в жидком состоянии с глубины, которая на порядок меньше трёх тысяч вёрст, рассчитывать, что оставшиеся километры корки обеспечат прочность вдесятеро больше, чем сталь, не приходится. Кроме того, остаётся тонкий вопрос — а что заставляет эту жидкую субстанцию распределяться именно по поверхности пузыря, а не свалиться в центр?
Хочу ещё заметить, что когда Жюль Верн или акад. Обручев писали свои романы о путешествиях если и не совсем к центру Земли, то достаточно далеко, они честно называли их «фантастикой».
Ну и теперь, покончив с десертом, вернёмся к первому блюду. Собсно, тут уже неоднократно объяснялось, как именно была рассчитана (!) масса Земли: из измерений гравитационной постоянной. Оная постоянная сейчас измерена уже с достаточно высокой точностью — 8 знаков после запятой. Чему удивляться не приходится — в конце концов, при обнаружении гравитационных волн регистрируется сдвиг пробной массы на величину, в тысячи раз меньшую размера протона. Так что смещение пробной массы на величину даже 1 мк — это на современном уровне техники измерений просто детская задачка. А масса в крутильных весах смещается на куда большую величину.
Ну а как только найдена величина гравитационной постоянной, остаётся только подставить её в формулу ускорения свободного падения и получить отсюда массу Земли. Ведь размер земли тоже известен, и тоже с высокой точностью. Надеюсь, объяснять, как измерен этот размер, не требуется…