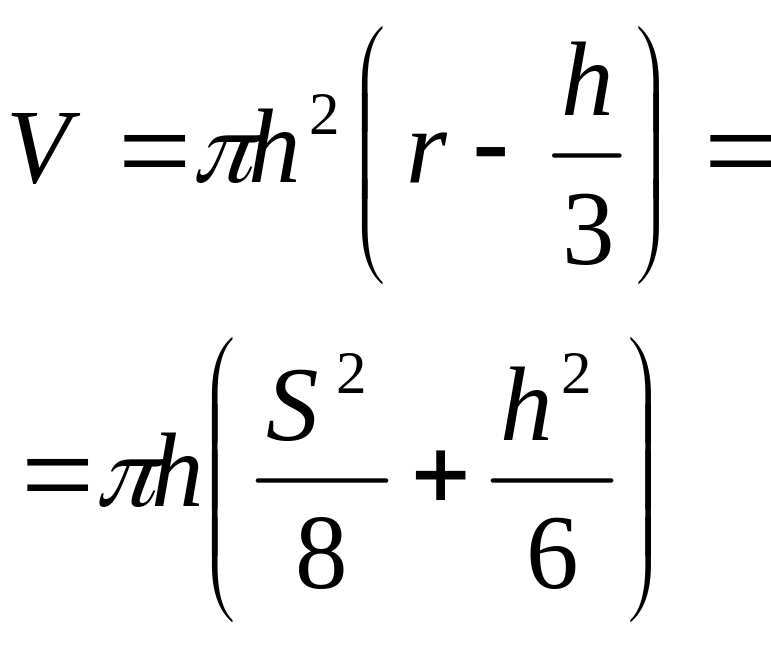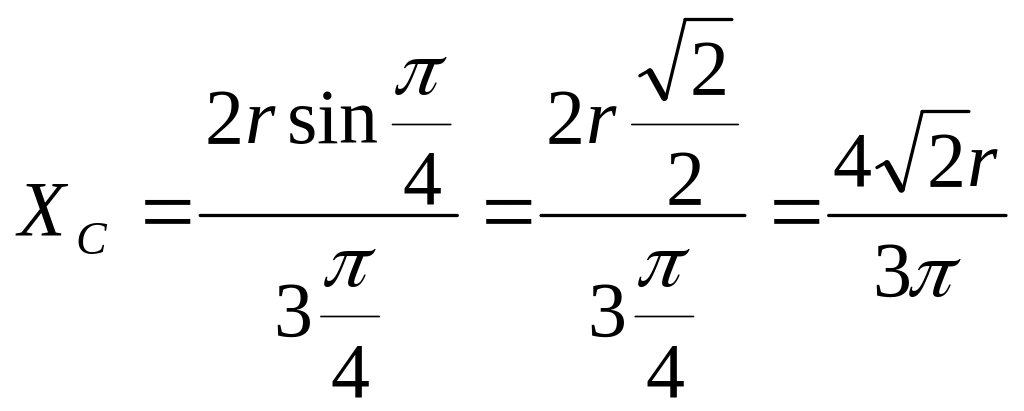Как найти массу зная только размер

Масса сплошной детали

Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).

Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей):

Объем сплошной детали — это… ее объем и больше ничего.

Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.

Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).

---

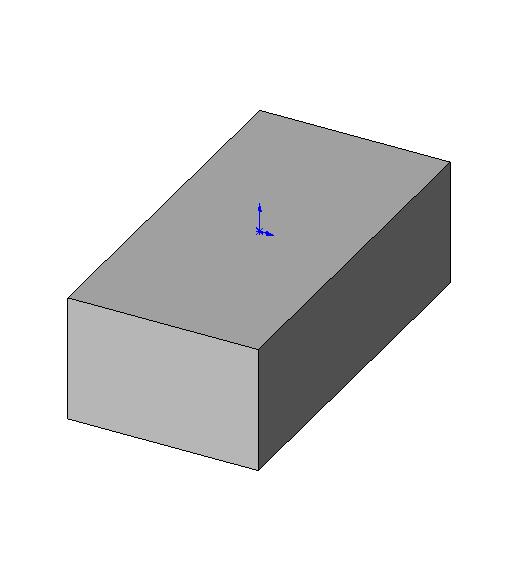
1. Масса параллелепипеда (бруска)

Объем параллелепипеда: , где — длина, — ширина, — высота.
Тогда масса:

---

2. Масса цилиндра

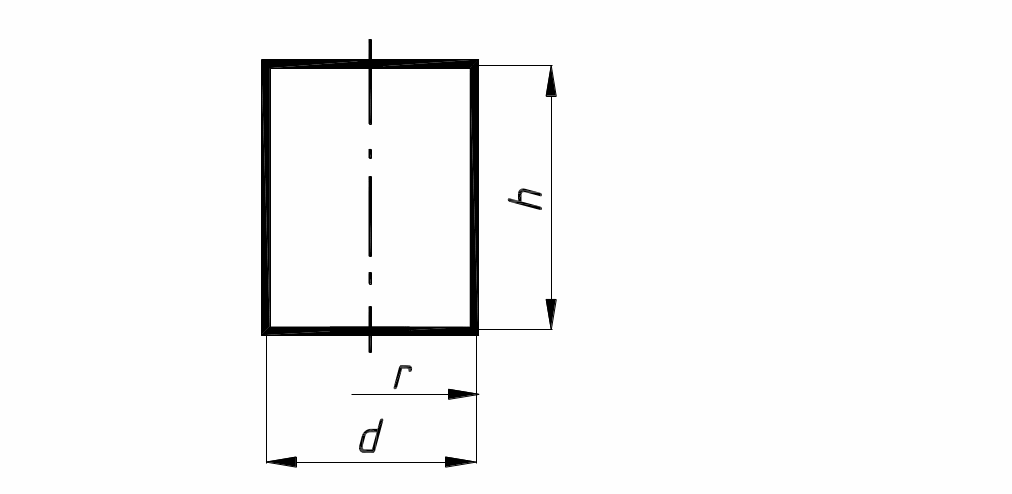
Объем цилиндра: , где — диаметр основания, — высота цилиндра.
Тогда масса:

---

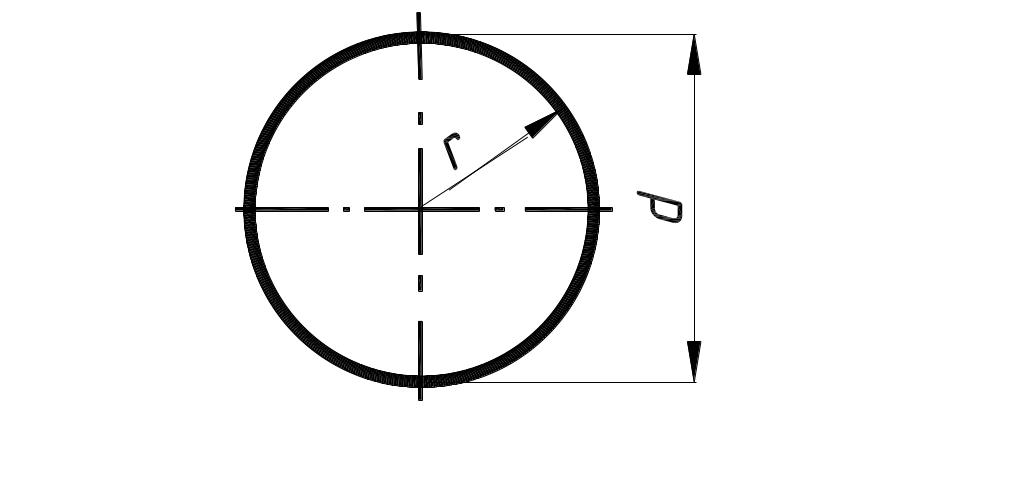
3. Масса шара

Объем шара: , где — диаметр шара.
Тогда масса:

---

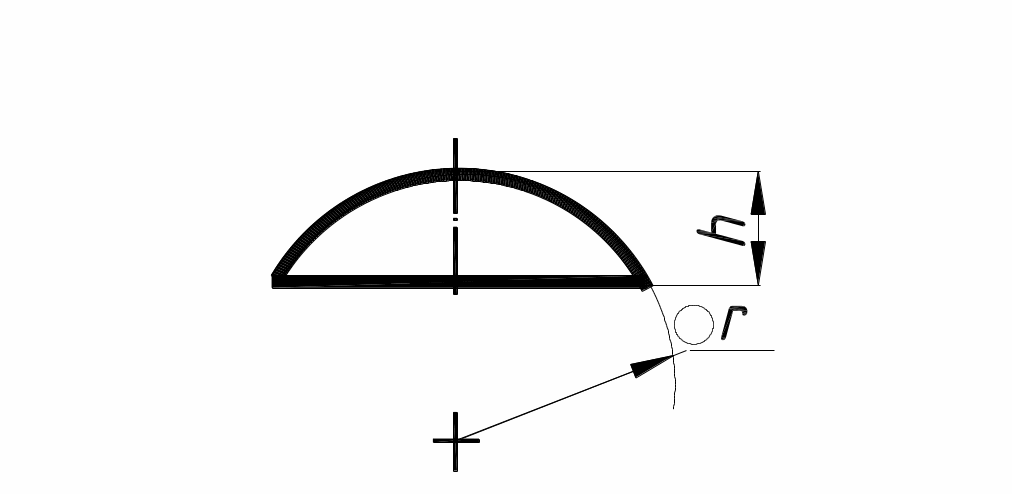
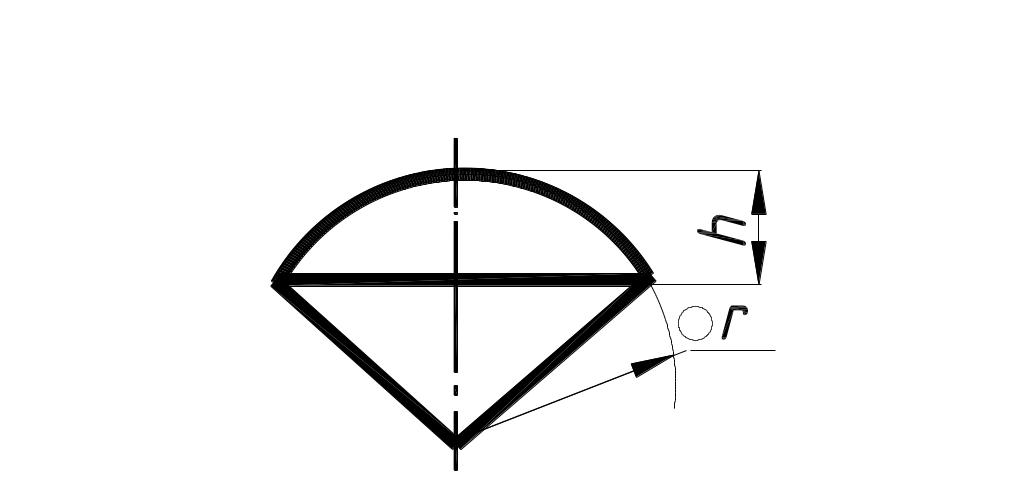
4. Масса сегмента шара

Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента.
Тогда масса:

---

5. Масса конуса

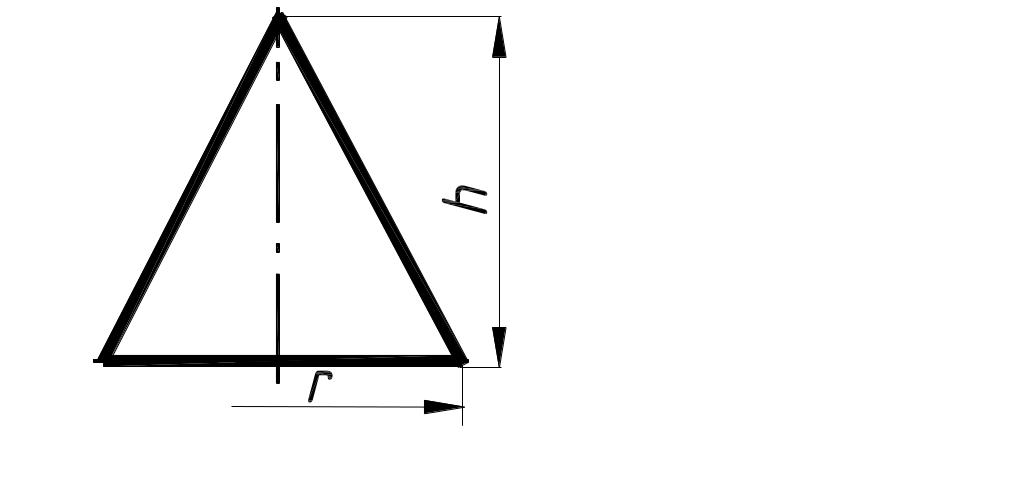
Объем любого конуса: , где — площадь основания, — высота конуса.
Для круглого конуса: , где — диаметр основания, — высота конуса.
Масса круглого конуса:

---

6. Масса усеченного конуса

Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем:
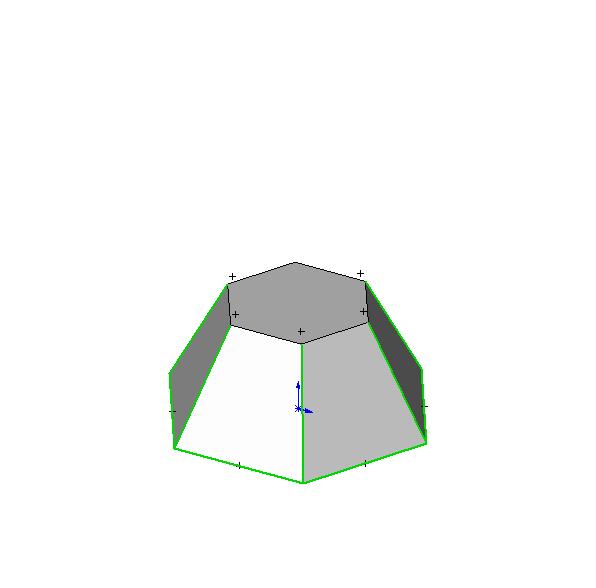
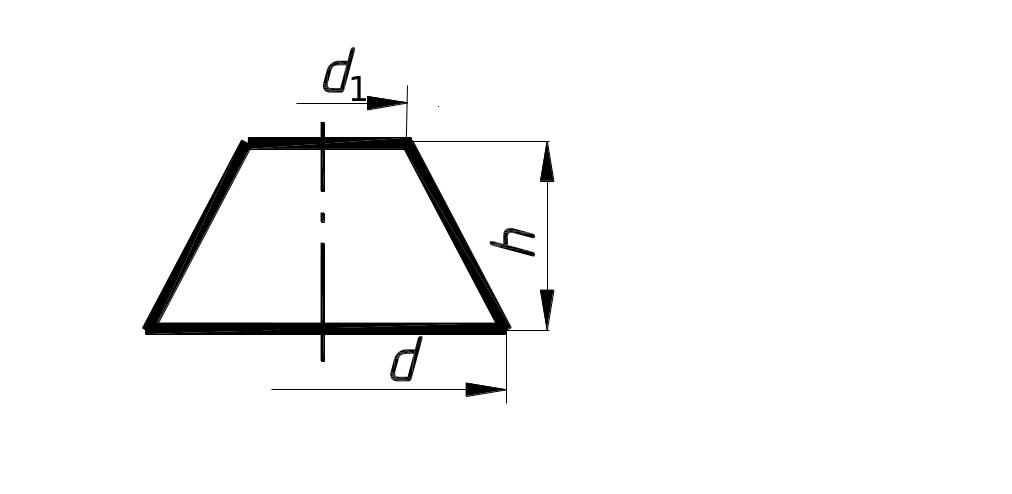
, где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса.
Отсюда масса:

---

7. Масса пирамиды

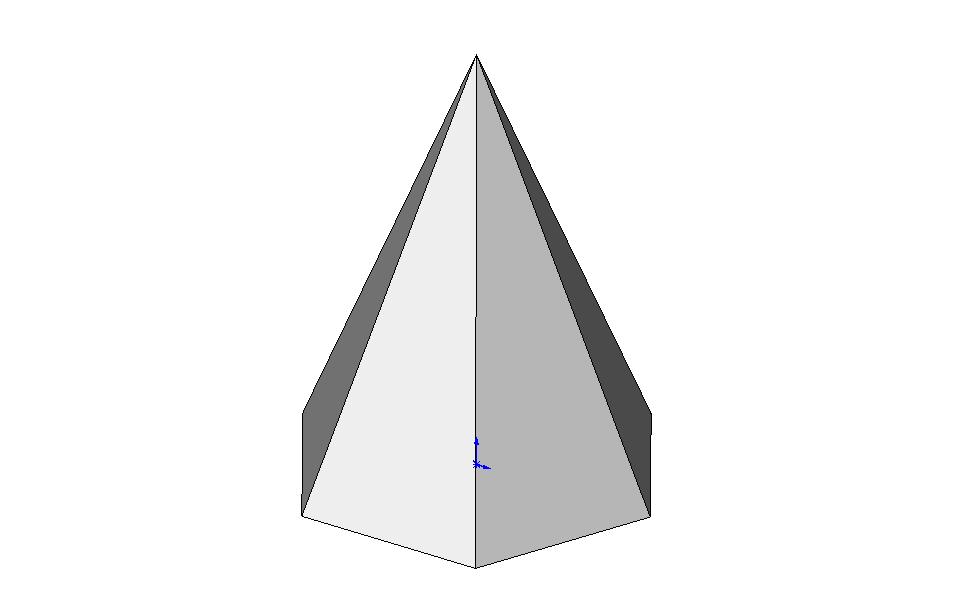
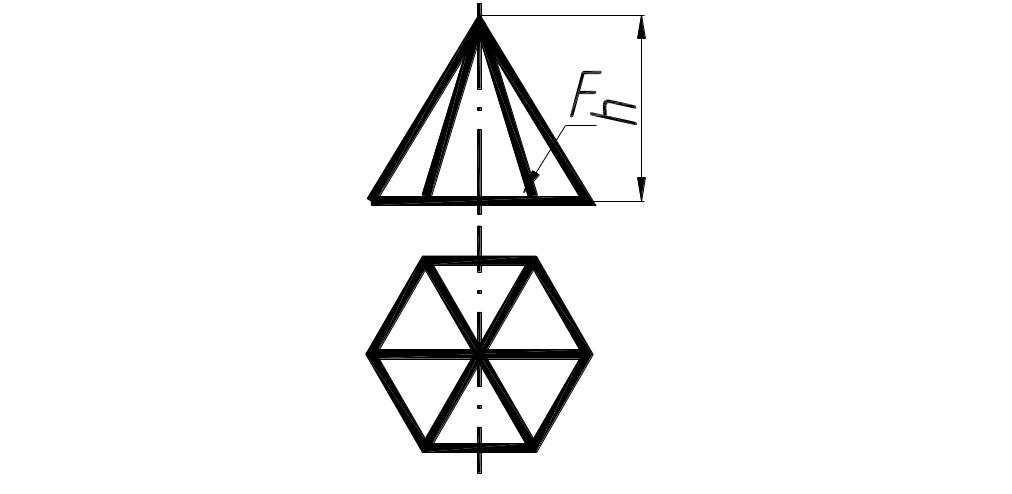
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.
Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды.
Тогда масса пирамиды:

---

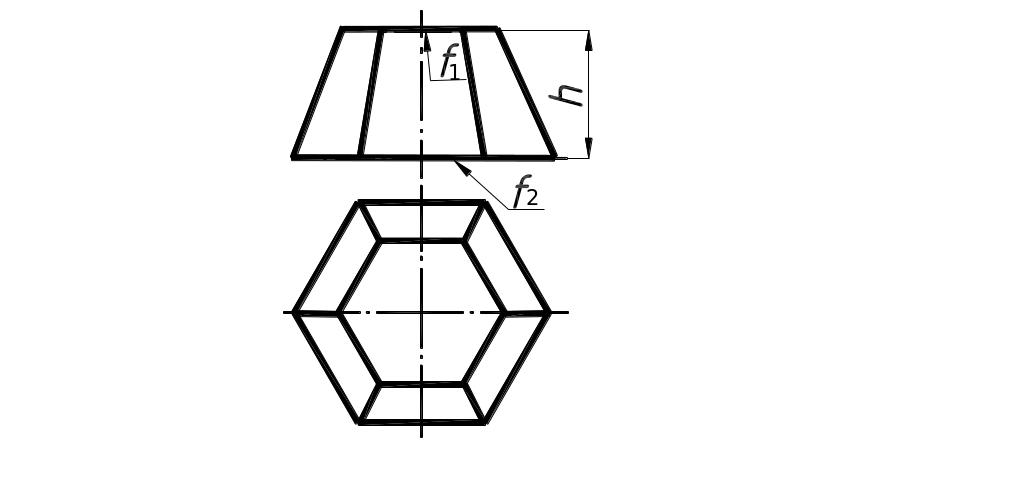
8. Масса усеченной пирамиды

Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , .
Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: .
Тогда масса усеченной прямоугольной пирамиды:

или

Для пирамиды с квадратным основанием (, ) формула выглядит проще:

---

Калькулятор массы

Для различных изделий сложной формы и профиля, с наличием прорезей и отверстий очень трудно рассчитать вес, а это очень важный момент – для транспортировки, для расчета монтажных параметров, для конструкторской документации и других целей. Процесс взвешивания также представляет собой сложности, особенно, когда изделия крупногабаритные – например, трубы, валы, турбины, металлические или деревянные конструкции, изделия из бетона и железобетона и т.д., или же вес небольшой детали, но сложной конфигурации.

Но, узнать точную массу таких изделий можно гораздо проще на нашем сайте

Мы предлагаем Вашему вниманию универсальный интерактивный калькулятор массы для самостоятельного расчета массы изделий самой разной формы из материалов цилиндрической или листовой формы. Его особенность в том, что он позволяет узнать вес детали или изделия не только из металлопроката и сплавов, но и любых других материалов: дерева и МДФ, пластиков и полимеров, бумаги, картона, резины, бетона, кирпича. Сделать это можно просто внеся габаритные показатели детали с вычетом размеров отверстий и прорезей, а также, величину коэффициента плотности материала, из которого деталь изготовлена. Точные данные можно найти в представленной рядом таблице.

Плотность  материалов
Наименование	Плотность ρ, кг/м3
Черные металлы
Сталь 10 ГОСТ 1050-88	7856
Сталь 20 ГОСТ 1050-88	7859
Сталь 40 ГОСТ 1050-88	7850
Сталь 60 ГОСТ 1050-88	7800
С235-С375 ГОСТ 27772-88	7850
Ст3пс ГОСТ 380-2005	7850
Чугун ковкий КЧ 70-2 ГОСТ 1215-79	7000
Чугун высокопрочный ВЧ35 ГОСТ 7293-85	7200
Чугун серый СЧ10 ГОСТ 1412-85	6800
Чугун серый СЧ20 ГОСТ 1412-85	7100
Чугун серый СЧ30 ГОСТ 1412-85	7300
Алюминий и сплавы алюминиевые
Силумин АК12ж ГОСТ 1583-93	2700
Сплав АК12 ГОСТ 1583-93	2710
Сплав АК5М ГОСТ 1583-93	2640
Сплав АК7 ГОСТ 1583-93	2700
Сплав АО9-1 ГОСТ 14113-78	2700
Магний и сплавы магниевые
Сплав ВМЛ9	1850
Сплав ВМЛ5	1890
Сплав МЛ10…МЛ19 ГОСТ 2856-79	1810
Баббиты оловянные и свинцовые
Б83 ГОСТ 1320-74	7380
Б87 ГОСТ 1320-74	7300
БН ГОСТ 1320-74	9550
Медь и медные сплавы
Бронза оловянная БрО10C10	8800
Бронза оловянная БрО19	8600
Бронза оловянная БрОC10-10	9100
Бронза оловянная БрОA10-1	8750
Бронза БрА10Ж3Мч2 ГОСТ 493-79	8200
Бронза БрА9Ж3Л ГОСТ 493-79	8200
Бронза БрМц5 ГОСТ 18175-78	8600
Латунь Л60 ГОСТ 15527-2004	8800
Латунь ЛА ГОСТ 1020-97	8500
Медь М0, М1, М2, М3 ГОСТ 859-2001	8940
Медь МСр1 ГОСТ 16130-90	8900
Титан и титановые сплавы
ВТ1-0 ГОСТ 19807-91	4500
ВТ14 ГОСТ 19807-91	4500
ВТ20Л ГОСТ 19807-91	4470
Фторопласты
Ф-4 ГОСТ 10007-80 Е	2100
Фторопласт — 1 ГОСТ 13744-87	1400
Фторопласт — 2 ГОСТ 13744-87	1700
Фторопласт — 3 ГОСТ 13744-87	2710
Фторопласт — 4Д ГОСТ 14906-77	2150
Термопласты
Дакрил-2М ТУ 2216-265-057 57 593-2000	1190
Полиметилметакрилат ЛПТ ТУ 6-05-952-74	1180
Полиметилметакрилат суспензионный ЛСОМ ОСТ 6-01-67-72	1190
Винипласт УВ-10 ТУ 6-01-737-72	1450
Поливинилхлоридный пластикат ГОСТ 5960-72	1400
Полиамид ПА6 блочный Б ТУ 6-05-988-87	1150
Полиамид ПА66 литьевой ОСТ 6-06-369-74	1140
Капролон В ТУ 6-05-988	1150
Капролон ТУ 6-06-309-70	1130
Поликарбонат	1200
Полипропилен ГОСТ 26996-86	900
Полиэтилен СД	960
Лавсан литьевой ТУ 6-05-830-76	1320
Лавсан ЛС-1 ТУ 6-05-830-76	1530
Стиролпласт АБС 0809Т ТУ 2214-019-002 03521-96	1050
Полистирол блочный ГОСТ 20282-86	1050
Сополимер стирола МСН ГОСТ 12271-76	1060
Полистирол ударопрочный УПС-0505 ГОСТ 28250-89	1060
Стеклопластик ВПС-8	1900
Стеклотекстолит конструкционный КАСТ-В ГОСТ 10292-74	1850
Винилискожа-НТ ГОСТ 10438-78	1440
Резина 6Ж ТУ 38-005-1166-98	1050
Резина ВР-10 ТР 18-962	1800
Стекло листовое ГОСТ 111-2001	2500
Стекло органическое техническое ТОСН ГОСТ 17622-72	1180
Прочие металлы
Вольфрам ВА ГОСТ 18903-73	19300
Вольфрам ВТ-7 ГОСТ 18903-73	19300
Золото Зл 99,9 ГОСТ 6835-2002	19300
Индий ИНО ГОСТ 10297-94	7300
Кадмий КдО ГОСТ 1467-93	8640
Олово О1пч ГОСТ 860-75	7300
Паладий Пд 99,8 ГОСТ 13462-79	12160
Платина Пд 99,8 ГОСТ 13498-79	21450
Свинец С0 ГОСТ 3778-98	11400
Серебро 99,9 ГОСТ 6836-2002	11500
Цинк Ц1 ГОСТ 3640-94	7130
Прочие материалы
Древесина, пробка	480
Древесина, лиственница	660
Древесина, липа	530
Древесина, ель	450
Древесина, сосна	520
Древесина, береза	650
Древесина, бук	690
Бумага	700-1200
Резина	900-2000
Кирпич	1400-2100
Фарфор	2300
Бетон	2000-2200
Цемент	2800-3000

При составлении сметы строительства или демонтажа металлоконструкций, покупке металлопроката или подготовке металлолома к сдаче, для найма подъемных механизмов бывает необходимо вычислить массу и количество металла, вес лома.

Как это сделать

Для получения необходимой информации можно обратиться к справочникам, и они рассчитают теоретический вес. Второй вариант – воспользоваться помощью калькулятора расчета веса металла по размерам. Если нет под рукой Интернета, есть простой выход – использовать школьные формулы вычисления массы по объему и плотности.

По справочникам

Сборник справочных материалов содержит таблицы металлов, по которым легко определить вес металлопроката любого вида, из черного и цветного металлов или сплавов. Кроме этого, в сборнике приведены формулы, чтобы посчитать вес металла по размерам для заготовок различных конфигураций, данные по удельному весу металлов.

К справочнику приходится обращаться при самостоятельном произведении математических расчетов, например, к таблице плотности металлов. Чтобы вычислить массу детали из цветного металла, понадобится переводной коэффициент.

С готовой таблицей легко самостоятельно рассчитать вес листа металла. По данной толщине и марке стали находится теоретический вес 1 м², искомая величина умножается на площадь листа. Особенно это удобно для стали с рифлением, выступами, цинковым напылением, учитывается также способ прокатки (холодный или горячий).

Упрощается просчет массы швеллера и двутавра – изделий со сложным сечением. Для них есть таблица с указанием номера профиля и соответствующего веса 1 пог. м в кг. Не нужно заморачиваться, чтобы вычислить вес стальной арматуры, к тому же в таблице указано количество погонных метров в 1 т.

Аналогичные таблицы существуют для металлических профилей Г-образного сечения: указан вес 1 м уголка для конкретной толщины и ширины полки. Правда, такие расчеты отличаются от фактического веса, так как таблицы составлены на основе ГОСТа. В реальности же прокат не всегда соответствует государственным стандартам.

Плотность стали зависит от температурных показателей. Все табличные данные соответствуют температуре 20°C. Данное замечание не относится к цветному прокату.

По калькулятору

Посчитать вес металла по размерам можно онлайн либо скачать калькулятор на компьютер (смартфон). Это удобный вид расчета, потому что не нужно перелистывать справочники в поисках нужных таблиц – достаточно задать конкретные параметры. С помощью калькулятора определяют вес железа любой марки и конфигурации с точностью до сотых долей:

• арматуры, прутков;
• листового проката;
• шестигранников, кругов, квадратов;
• труб;
• плит;
• уголков, швеллеров, двутавров.

Существуют также калькуляторы для цветного проката и для определения объемного веса металла, который важно знать для грузоперевозок.

Алгоритм работы с калькулятором простой:

1. Выбирается тип проката, вид изделия и марка металла.
2. Заносятся результаты замеров.
3. Нажимается кнопка «Посчитать».

Особенно удобна калькуляция для изделий с нестандартной и сложной формой. Кроме того, можно определять метраж изделия по его весу, т.е. переводить килограммы в метры.

Расчет веса по математическим формулам

Вес любого изделия находится так: M = ρV (ρ – плотность, V – объем изделия) или по формуле массы через площадь сечения: M = ρSL (S — площадь сечения, L — длина). Для углеродистой стали принято использовать усредненное значение ρ, равное 7850 кг/м³ или 0,00785 г/мм³, либо 7,85 г/см³ (в зависимости от выбранных единиц измерений). Самое простое вычисление – это масса стального куба со стороной 1 м. Она равна 7850 кг, или 7,85 т.

Различают практические и теоретические формулы массы. Первые адаптированы к определенным условиям, чтобы облегчить и ускорить расчеты.

Листовой прокат

Для расчета веса листового металла нужно перемножить 3 измерения – длину, ширину и толщину изделия, полученный результат умножить на плотность металла. Например: длина проката 1 м, ширина – 2 м, толщина – 2мм, тогда M = 1×2×0,002×7850 = 31,4 (кг).

При определении массы нескольких одинаковых листов железа, достаточно рассчитать вес 1 листа и умножить на количество.

Пруток, проволока и арматура

Для определения массы прутка или любого изделия круглого сечения, используется такая теоретическая формула: M= πR²Lρ, где L – длина, R – радиус заготовки, π = 3,14, ρ – плотность металла. Другая, практическая, формула: M = (0,02466R²)L. Ее можно использовать и для рифленой арматуры.

Из объема найти массу прямоугольного прутка совсем просто. Нужно перемножить длину, ширину и толщину (это объём V), затем найти в справочнике соответствующую плотность и умножить ее на V: M = ABLρ, где A, B – ширина и толщина.

Круг

Чтобы найти вес металлического круга, нужно подставить числовые значения в формулу: M = πR²dρ (R– радиус, d – толщина).

Шестигранный пруток

Лучше всего обратиться за помощью к готовым таблицам, но в их отсутствии расчеты можно произвести самостоятельно:

M = (3√3/2)а²Lρ,

где а – длина стороны шестигранника (мм), L – длина прутка (мм), ρ = 0,00785 г/мм³.

Прямоугольный профиль

Узнать массу прямоугольной профильной трубы можно так:

M = 2(a+b)sLρ,

где a и b – ширина и высота сечения (мм), s – толщина стенки (мм), L – длина трубы (мм), ρ = 0,00785 г/мм³ . Если стенки разной толщины, проводится несколько измерений и находится среднее значение.

Масса круглой трубы

Посчитать вес металла по размерам в данном случае можно по следующим формулам:

M = π(R² – r²)Lρ, M = 2πRsLρ, M = (D-s)s×0,2466

где М – масса, R² – внешний радиус, r² – внутренний радиус, L – длина трубы, ρ_. – плотность стали, s – толщина стенки, 0,2466 – константа, соответствующая плотности углеродистой стали ρ = 7,85 г/см³.

Трубу с закрытым концом можно рассматривать как бочку и применить для нахождения ее веса представленные выше формулы для трубы и круга.

Вес фигурных изделий

Посчитать массу, зная объем и плотность, можно для изделий любой конфигурации. Нужно только правильно вычислить объем и подставить значение в известную формулу M = Vρ.

Объем пирамиды рассчитывается по формуле: V = 1/3 SH, где S – площадь основания, H – высота пирамиды.

Для усеченной пирамиды V = 1/3 h(F + f + √Ff), где F и f – площади большего и меньшего основания.

Объем цилиндра: V = πR²H.

Объем конуса: V = 1/3 πR²H, объем усеченного конуса: V = 1/3 πH(R² + Rr + r²), где H – высота, R и r – радиусы большего и меньшего основания.

Объем шара: V = πD³/6 (D – диаметр).

Для уголка: V = s(h₁ + h₂)L, где L – длина уголка, s – толщина металла, h₁ и h₂ – ширина полок.

Объем изделия витиеватой формы и небольших габаритов находят по количеству вытесненной жидкости, поместив его в емкость с водой.

Если конструкция изготовлена из разных металлов и сплавов, тогда можно найти ее массу через вес отдельных деталей.

Теоретический вес рассчитывается по формулам, практический (фактический) определяется взвешиванием. Естественно, что всегда между этими величинами будет несоответствие. Расчет массы заготовки, произведенный самостоятельно по математическим формулам, также может отличаться от табличных или же выданных калькулятором.

Для получения более точных результатов целесообразно пользоваться данными справочников или электронных вычислительных устройств.

1. Определение массы детали по ее чертежу

Масса детали
определяется

G
= V,

где V
– объем детали, 
‑ плотность материала из которого
изготовлена данная деталь.

Таким образом,
для определения массы детали необходимо
определить объем детали. Для этого
разбиваем деталь на фигуры, для которых
можно определить объем детали по
известным формулам (табл. 2.1)

Таблица 2.1

Наим.	Наглядное изображение	Эскиз	Объем
1	2	3	4
Цилиндр
Призма			V = аbc
Пирамида			площадь основания

Продолжение табл.
2.1

1	2	3	4
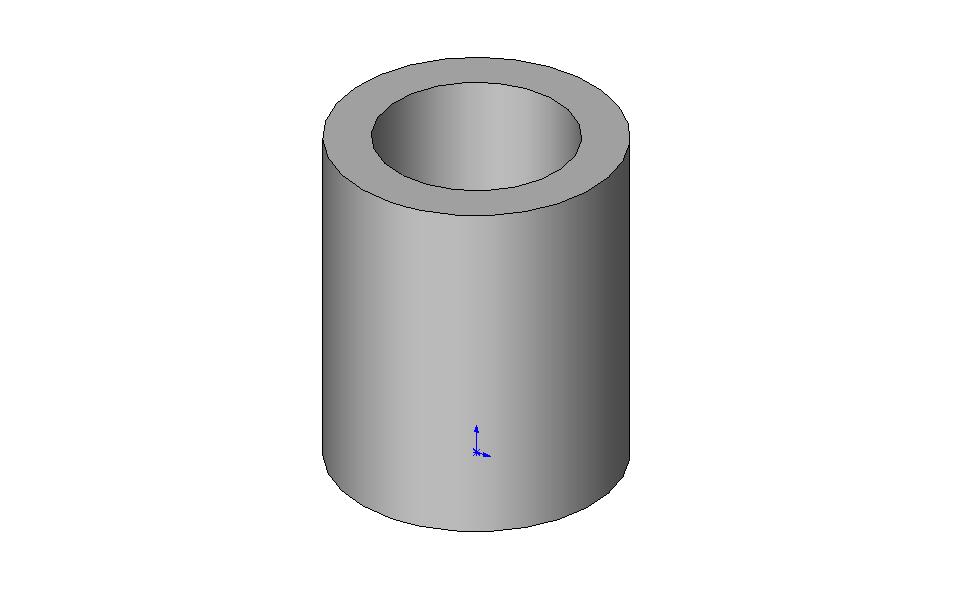
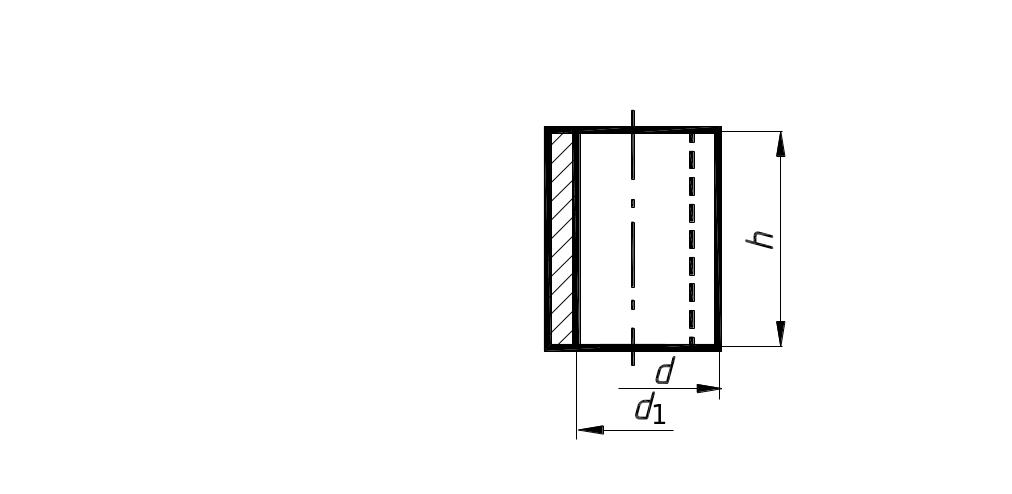
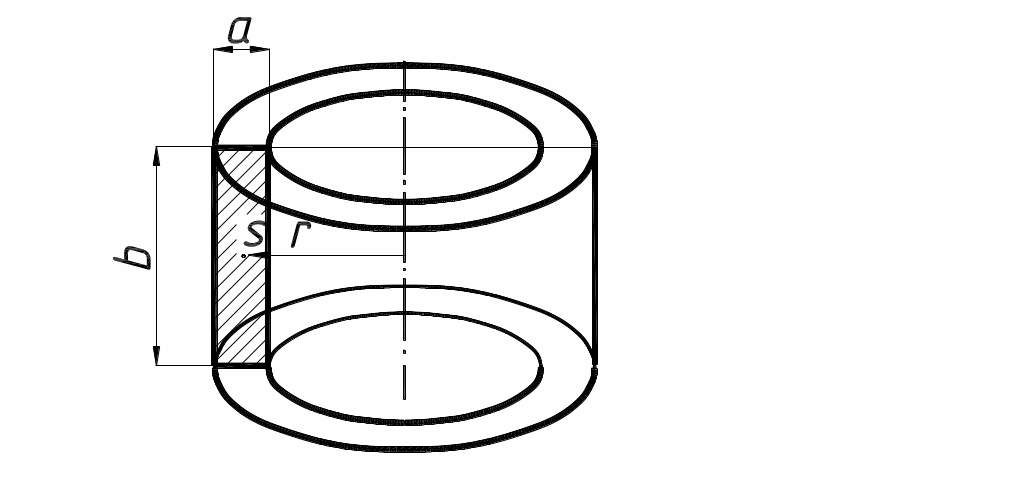
Полый цилиндр
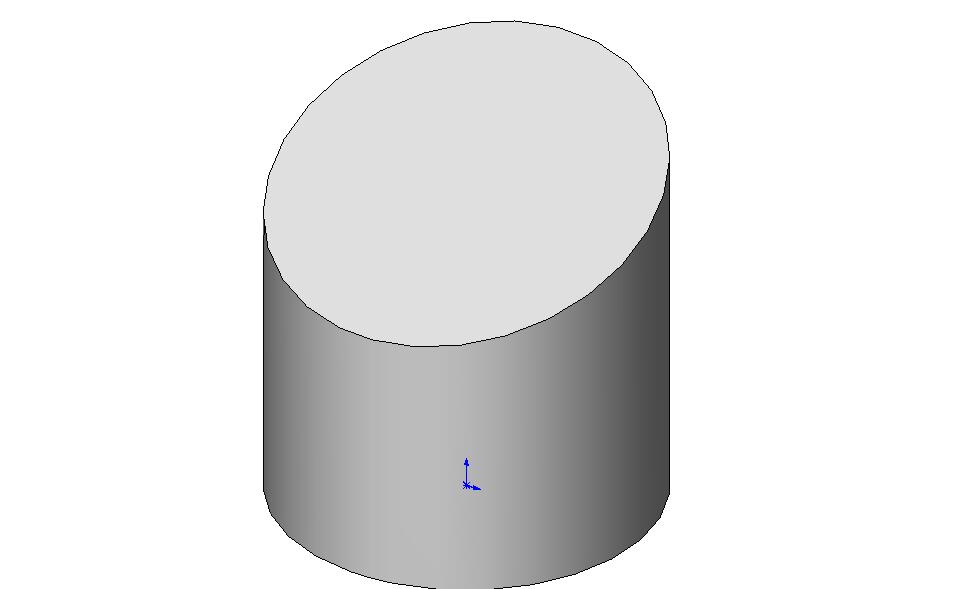
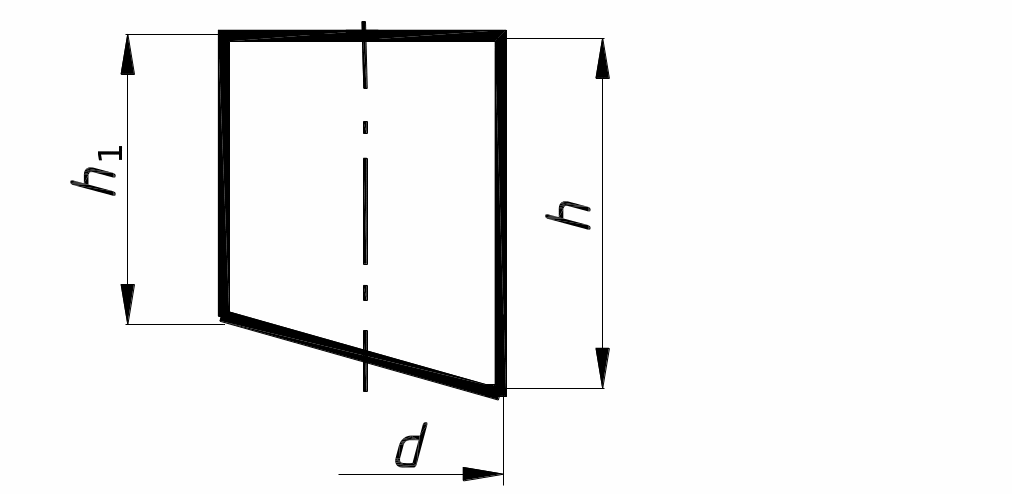
Косо срезанный цилиндр
Шар
Шаровой сектор
Шаровой сегмент

Продолжение табл.
2.1

1	2	3	4
Конус
Усеченная пирамида			, где f1 и f2 – площади оснований пирамиды
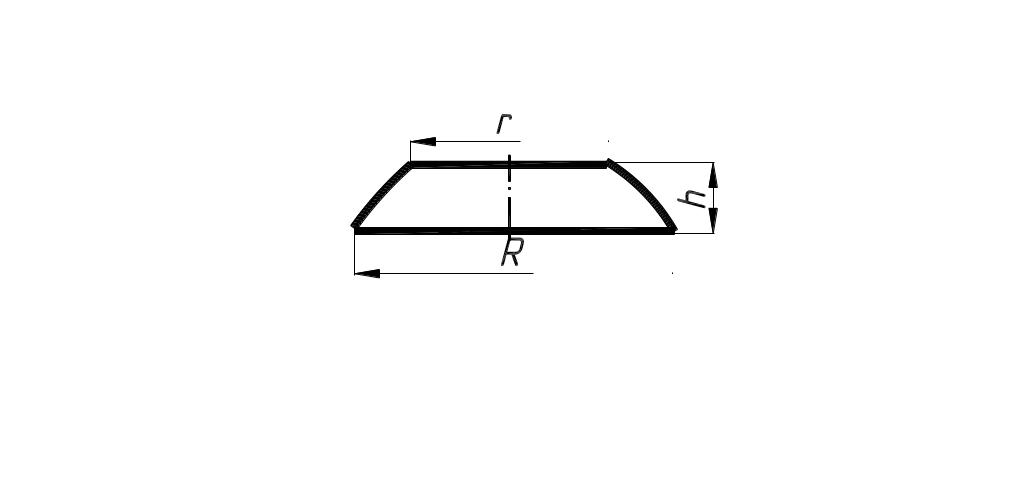
Усеченный конус
Бочка
Тело вращения		Объем V тела вращения, образованного вращением площади F, умноженной на путь, описанный ее центром тяжести S вокруг оси радиусом r V=2rF=2rab

В качестве примера
рассмотрим определение объема вала,
изображенного на рис. 2.1. Разобьем вал
на простые (с точки зрения вычисления
объема) тела (рис. 2.2) и вычислим их объем.

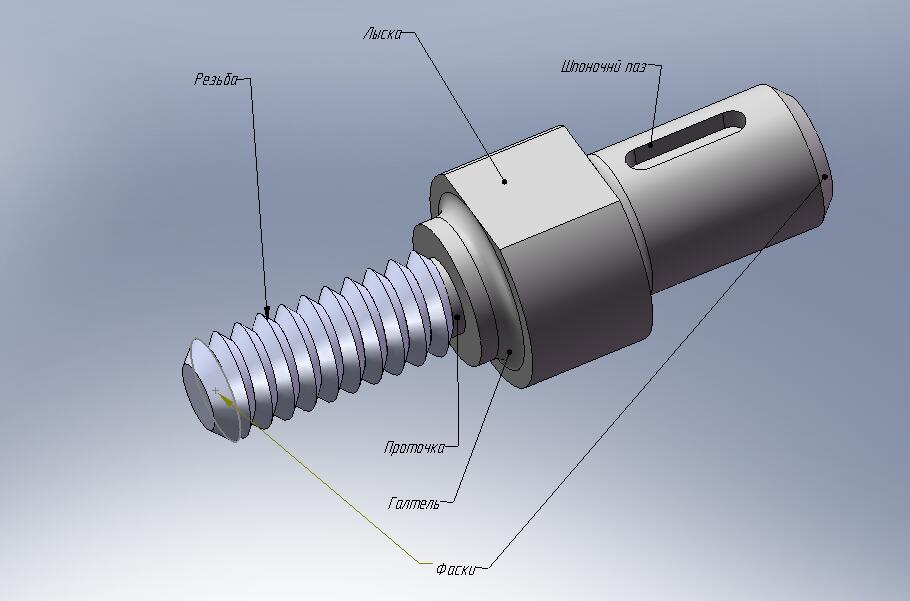
Рис.2.1

1. Объем фаски (1) –
усеченный конус (рис. 2.2)

,

где h
= 2 мм; r
= d/2=6
мм; r₁
= r
– 2 = 4 мм.

Тогда

.

1. Объем цилиндра
   (2)

.

Рис. 2.2

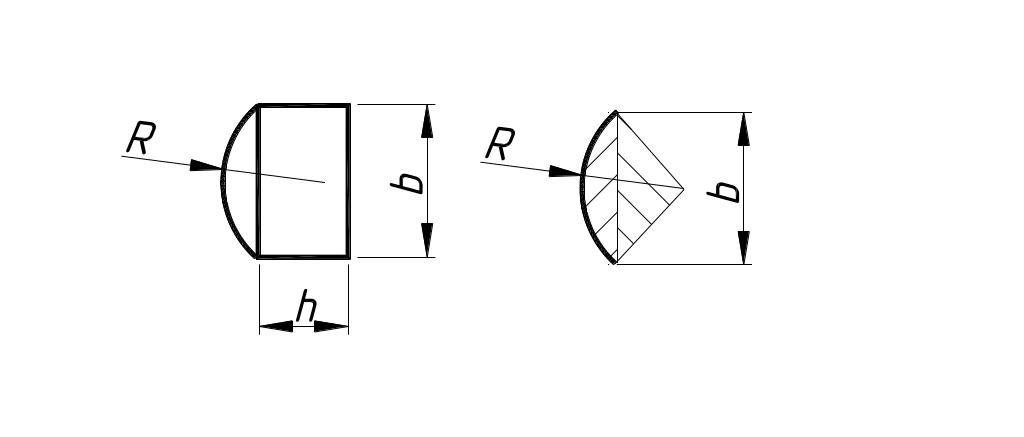
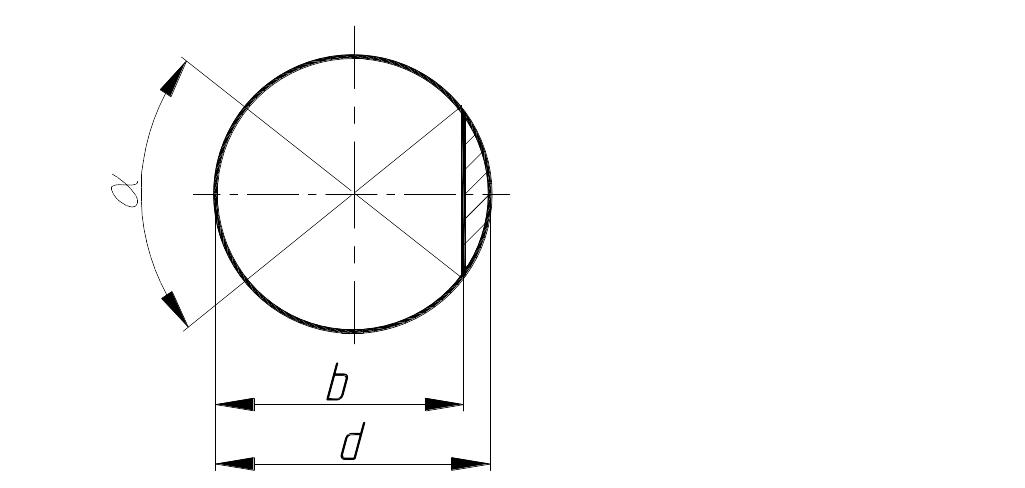
3. Объем паза (3) с
поперечным сечением S
(рис. 2.3, а)
и длиной 10 мм для призматической части
паза

а б

Рис. 2.3

,

где S
= S_сег.
+
S_пр,
S_сег.
– площадь сегмента с радиусом R,
S_пр
– площадь прямоугольника b
ĥ
h,
б.
S_сег.
=
S_сек.
– S_тр.
S_сек.
– площадь
сектора круга, S_тр
– площадь треугольника – рис. 2.3

S_сег.
=
S_сек.
– S_тр=

здесь

S_пр
= b
ĥ
h
= 5∙10 = 50 мм²,

S
= S_сег.
+
S_пр
= 16,16 + 50 =66,16 мм²

.

Учтем объем цилиндра
от боковых полуцилиндров паза. Примем

r
=b/2
= 2,5 мм
– радиус цилиндра,

h^/
= h
+ 0,5(R
—

)
= 3 + 0,5(6 –


‑ высота

цилиндра равная
глубине паза и верхнюю часть цилиндра
паза.

Тогда объем
цилиндрической части шпоночного паза,
получим:

V_ц
≈
πr²h^/=π6,25∙3,27
= 64,2 мм³

Окончательно объем
шпоночного паза будет

V₃
= V_пр
+ V_ц
= 661,6+64,2 = 725,8 мм³

4. Объем галтели 4
с радиусом r
= 1 мм
(рис. 2.4).

Площадь галтели
определится как разность площадей
квадрата S_к
= r²
и четверти
круга (сектора) S_c
= r²/4
(рис. 2.4)

S_г
= r²
— r²/4
= r²(4-
)/4=
1²(4-π)/4
= 0,22 мм²

Р

ис.
2.4

Центр тяжести
вдоль оси Х
квадрата x_К
=

,
а четверти круга – сектора круга с углом
90º

,

Центр тяжести
галтели вдоль оси X:

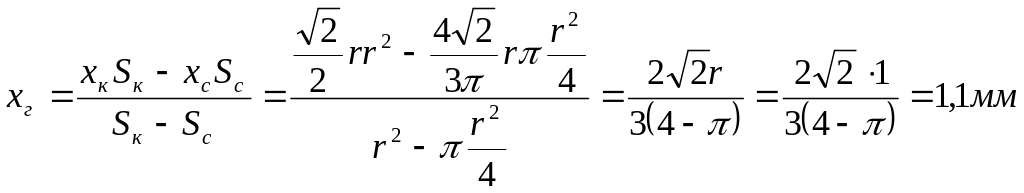
5. Объем лыски (рис.
2.5) 5:

V₅
= S_сег.h

Площадь сегмента
S_сег.
определится
как разность площади сектора с углом α
и площади треугольника

S_сег.=
S_сек.
– S_тр=

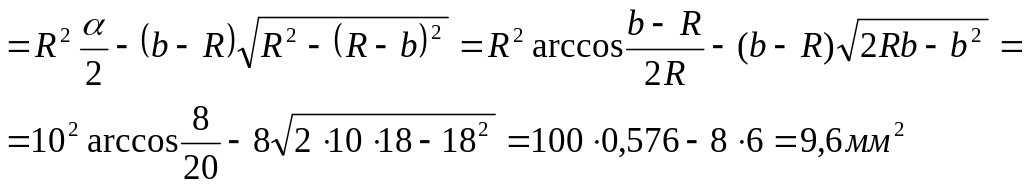
Находим численное
значение объема лыски

V₅
= S_сег.h
= 9,6∙15 = 144
мм³

Рис. 2.5

6. Объем цилиндра
(6)

.

7. Объем цилиндра
(7,8)

,

где р=
1,5 мм
– шаг резьбы.

8. Объем резьбы

V₉
= SLn,

где S=p²tg60^o/4,
L
= 2πr
– длина
витка резьбы, n
= l/p
– количество витков, l
‑ длина резьбы.

Тогда

V₉
= 2πr
p²tg60^o
l/4p
= πr
ptg60^o
l/2
= π5∙1,5∙1,732∙12/2
= 245 мм³

9. Фаска 10:

.

Окончательно,
складываем все объемы, вычитая объем
лыски и шпоночного паза, получим

V₁ + V₂
— V₃ +V₄
— V₅ + V₆
+ V_7,8 + V₉
+ V₁₀
= 160 + 2035,75 – 725,8 + 16,76 -144 + 4712,4 + 3329 + 245 + 63,87
= 9693,8 мм³.

Массу тела получим,
используя ранее приведенную формулу m
= V.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #