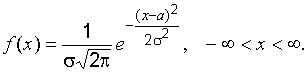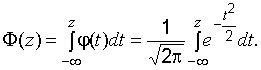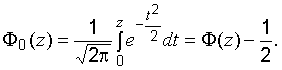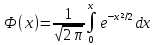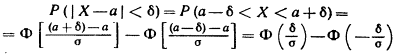Как найти мат ожидание нормальной величины - Исправление недочетов и поиск решений вместе с Examum.ru

Нормальное распределение, его математическое ожидание, дисперсия.

Случайная
величина называется
распределенной по нормальному закону,
если ее плотность вероятности имеет
вид:

Здесь  математическое
ожидание,  дисперсия,  среднее
квадратическое отклонение. Как и
ранее, ,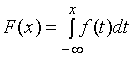
однако, этот интеграл вычисляется
численными методами. Чтобы упростить
эту процедуру, пользуются преобразованием
случайной величины  и
правилом сохранения элемента вероятности ,
где  плотность
распределения вероятности случайной
величины :

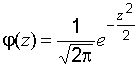
Как
видим, индивидуальные числовые
характеристики распределения
(математическое ожидание и дисперсия)
в последнее выражение не входят, т.е.
вышеуказанным преобразованием нормальная
случайная величина приведена
к нормальной стандартной случайной
величине с
параметрами 0 (математическое ожидание)
и 1 (дисперсия). Дифференциальная и
интегральная функции стандартного
нормального распределения табулированы
(имеются таблицы), что существенно
облегчает вычисления. Интегральная
функция распределения обозначается ,

Часто
используют функцию Лапласа:

Очевидны
следующие свойства:

где .

Пример.
Нормальная
случайная величина  задана
математическим ожиданием  и
средним квадратическим отклонением .
Записать соответствующую дифференциальную
функцию, схематично изобразить ее
график, вычислить вероятность попадания
случайной величины  в
интервал

Решение:
Записать дифференциальную функцию
нормальной случайной величины с
заданными значениями математического
ожидания и дисперсии значит в общее
выражение для дифференциальной функции
нормальной случайной величины подставить
заданные и .
Например, если ,
то получим

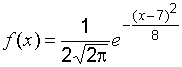
При
изображении этой функции на схематичном
графике следует учесть, что эта функция
имеет максимум при ,
симметрична относительно  (это
видно непосредственно из приведенной
выше формулы) и стремится к нулю при .
Однако правило (вероятность
того, что случайная величина примет
значение, по модулю отличающееся от
математического ожидания на или
более, пренебрежимо мала – составляет
всего около 0,0027) позволяет нам закончить
правую ветвь в точке  а
левую – в точке  Высота
максимума в точке  составит  Дополнительно
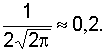
надо учесть, что перегибы ветвей будут
иметь место в точках

Вероятность
попадания случайной величины в
интервал вычислим
так:

При
этом следует воспользоваться таблицами
функции стандартного нормального
распределения или
функции Лапласа .

36. Нормальная кривая.

Центральная
предельная теорема. Если
случайная величина Х представляет собой
сумму очень большого числа взаимно
независимых случайных величин, влияние
каждой из которых на всю сумму ничтожно
мало, то Х имеет распределение, близкое
к нормальному.

Говорят,
что случайная величина Х распределена
по нормальному
закону с
параметрами а и ,
если плотность распределения вероятностей
имеет вид:

,
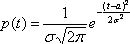
–¥<t<¥.

Вероятностный
смысл параметров а и таков: а –
математическое ожидание случайной
величины Х, s –
среднее квадратическое отклонение
величины.

Иногда
такой закон распределения
называют Гауссовским. График плотности
нормального распределения называют
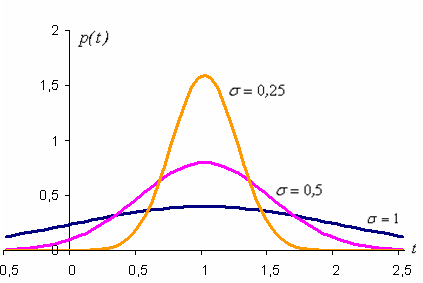
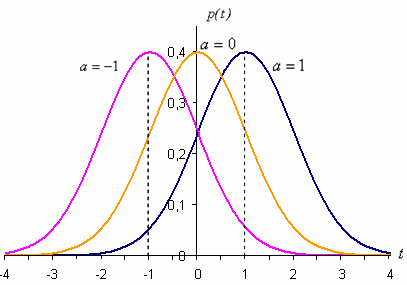
нормальной кривой (кривой Гаусса). На
рисунке изображены нормальные кривые
с параметрами а=1
и , , .

Из
рисунка видно, что положение пика кривых
определяется параметром а=1,
а параметр s (среднее квадратическое отклонение)
характеризует форму нормальной кривой.
При увеличении s уменьшается
максимум кривой распределения, сама
кривая становится более пологой,
растягиваясь вдоль оси абсцисс. И,
наоборот, при уменьшении s возрастает
максимум кривой распределения, сама
кривая становится более «островершинной».
Площадь, ограниченная любой нормальной
кривой и осью абсцисс, равна единице.
Параметр а(математическое
ожидание величины) определяет положение
максимума на оси абсцисс, не влияя на
форму кривой. На рисeyrt
ниже показаны нормальные кривые с
одинаковым средним квадратическим отклонением и
разными математическими
ожиданиями а=–1, а=0, а=1.

Нормальное
распределение с параметрами а=0
и называется нормированным.

Вероятность
попадания в заданный интервал нормальной
случайной величины.

Вероятность
того, что Х примет значение, принадлежащее
интервалу (α,β)

P(α<X<β)=Ф((β-a)/σ)-Ф((α-a)/σ),
где

– функция Лапласа.

Ф(-∞)=0
Ф(+∞)=1
Ф(-х)=1-Ф(х)

P(mx-l<x<mx+l)=Ф(l/σ)-Ф(-l/σ)=2Ф(l/σ)-1

38.
Вычисление вероятности заданного
отклонения.

Часто
требуется вычислить вероятность того,
что отклонение нормально распределенной
случайной величины Х по
абсолютной величине меньше заданного
положительного числа d, т.
е. требуется найти вероятность
осуществления неравенства |x —а|<d.

Заменим
это неравенство равносильным ему двойным
неравенством

Тогда
получим:

Приняв
во внимание равенство:

(функция
Лапласа—нечетная), окончательно имеем

Вероятность
заданного отклонения равна

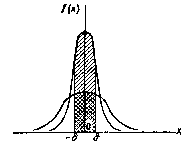
На
рисунке наглядно показано, что если две
случайные величины нормально распределены
и а = 0,
то вероятность принять значение,
принадлежащее интервалу (-d,d),больше
у той величины, которая имеет меньшее
значение d. Этот
факт полностью соответствует вероятностному
смыслу параметра s .

Пример.
Случайная величина Х распределена
нормально. Математическое ожидание и
среднее квадратическое
отклонение Х соответственно
равны 20 и 10. Найти вероятность того, что
отклонение по абсолютной величине будет
меньше трех.

Решение: Воспользуемся
формулой

По
условию ,

тогда

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Нормальным называют распределение вероятностей непрерывной случайной величины

, плотность которого имеет вид:

где

–
математическое ожидание,

–
среднее квадратическое отклонение

Вероятность того, что

примет
значение, принадлежащее интервалу

где

– функция Лапласа:

Вероятность того, что абсолютная
величина отклонения меньше положительного числа

В частности, при

справедливо
равенство:

Асимметрия, эксцесс,
мода и медиана нормального распределения соответственно равны:

, где

Правило трех сигм

Преобразуем формулу:

Положив

. В итоге получим

если

, и, следовательно,

, то

то есть вероятность того, что
отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонение, равна 0,9973.

Другими словами, вероятность того,
что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна
0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие
события исходя из принципа невозможности маловероятных
событий можно считать практически невозможными. В этом и состоит
сущность правила трех сигм: если случайная величина распределена нормально, то
абсолютная величина ее отклонения от математического ожидания не превосходит
утроенного среднего квадратического отклонения.

На практике правило трех сигм
применяют так: если распределение изучаемой случайной величины неизвестно, но
условие, указанное в приведенном правиле, выполняется, то есть основание
предполагать, что изучаемая величина распределена нормально; в противном случае
она не распределена нормально.

Смежные темы решебника:

Таблица значений функции Лапласа
Непрерывная случайная величина
Показательный закон распределения случайной величины
Равномерный закон распределения случайной величины

Пример 2

Ошибка
высотометра распределена нормально с математическим ожиданием 20 мм и средним
квадратичным отклонением 10 мм.

а) Найти
вероятность того, что отклонение ошибки от среднего ее значения не превзойдет 5
мм по абсолютной величине.

б) Какова
вероятность, что из 4 измерений два попадут в указанный интервал, а 2 – не
превысят 15 мм?

в)
Сформулируйте правило трех сигм для данной случайной величины и изобразите
схематично функции плотности вероятностей и распределения.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

а) Вероятность того, что случайная величина, распределенная по
нормальному закону, отклонится от среднего не более чем на величину

В нашем
случае получаем:

б) Найдем
вероятность того, что отклонение ошибки от среднего значения не превзойдет 15
мм:

Пусть событие

– ошибки 2
измерений не превзойдут 5 мм и ошибки 2 измерений не превзойдут 0,8664 мм

– ошибка не
превзошла 5 мм;

– ошибка не
превзошла 15 мм

в)
Для заданной нормальной величины получаем следующее правило трех сигм:

Ошибка высотометра будет лежать в интервале:

Функция плотности вероятностей:

График плотности распределения нормально распределенной случайной величины

Функция распределения:

График функции
распределения нормально распределенной случайной величины

Задача 1

Среднее
количество осадков за июнь 19 см. Среднеквадратическое отклонение количества
осадков 5 см. Предполагая, что количество осадков нормально-распределенная
случайная величина найти вероятность того, что будет не менее 13 см осадков.
Какой уровень превзойдет количество осадков с вероятностью 0,95?

Задача 2

Найти
закон распределения среднего арифметического девяти измерений нормальной
случайной величины с параметрами m=1.0 σ=3.0. Чему равна вероятность того, что
модуль разности между средним арифметическим и математическим ожиданием
превысит 0,5?

Указание:
воспользоваться таблицами нормального распределения (функции Лапласа).

Задача 3

Отклонение
напряжения в сети переменного тока описывается нормальным законом
распределения. Дисперсия составляет 20 В. Какова вероятность при изменении
выйти за пределы требуемых 10% (22 В).

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 4

Автомат
штампует детали. Контролируется длина детали Х, которая распределена нормально
с математическим ожиданием (проектная длинна), равная 50 мм. Фактическая длина
изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что
длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.

Задача 5

Случайная
величина X распределена нормально с математическим ожиданием a=10и средним
квадратическим отклонением σ=5. Найти
интервал, симметричный относительно математического ожидания, в котором с
вероятностью 0,9973 попадает величина Х в результате испытания.

Задача 6

Заданы
математическое ожидание a_x=19 и среднее квадратическое отклонение σ=4
нормально распределенной случайной величины X. Найти: 1) вероятность
того, что X примет значение, принадлежащее интервалу (α=15;
β=19); 2) вероятность того, что абсолютная величина отклонения значения
величины от математического ожидания окажется меньше δ=18.

Задача 7

Диаметр
выпускаемой детали – случайная величина, распределенная по нормальному закону с
математическим ожиданием и дисперсией, равными соответственно 10 см и 0,16 см².
Найти вероятность того, что две взятые наудачу детали имеют отклонение от
математического ожидания по абсолютной величине не более 0,16 см.

Задача 8

Ошибка
прогноза температуры воздуха есть случайная величина с m=0,σ=2℃. Найти вероятность
того, что в течение недели ошибка прогноза трижды превысит по абсолютной
величине 4℃.

Задача 9

Непрерывная
случайная величина X распределена по нормальному
закону: X∈N(a,σ).

а) Написать
плотность распределения вероятностей и функцию распределения.

б) Найти
вероятность того, что в результате испытания случайная величина примет значение
из интервала (α,β).

в) Определить
приближенно минимальное и максимальное значения случайной величины X.

г) Найти
интервал, симметричный относительно математического ожидания a, в котором с
вероятностью 0,98 будут заключены значения X.

a=5; σ=1.3;
α=4; β=6

Задача 10

Производится измерение вала без
систематических ошибок. Случайные ошибки измерения X
подчинены нормальному закону с σ_x=10. Найти вероятность того, что измерение будет
произведено с ошибкой, превышающей по абсолютной величине 15 мм.

Задача 11

Высота
стебля озимой пшеницы — случайная величина, распределенная по нормальному закону
с параметрами a = 75 см, σ = 1 см. Найти вероятность того, что высота стебля:
а) окажется от 72 до 80 см; б) отклонится от среднего не более чем на 0,5 см.

Задача 12

Деталь,
изготовленная автоматом, считается годной, если отклонение контролируемого
размера от номинала не превышает 10 мм. Точность изготовления деталей
характеризуется средним квадратическим отклонением, при данной технологии
равным 5 мм.

а)
Считая, что отклонение размера детали от номинала есть нормально распределенная
случайная величина, найти долю годных деталей, изготовляемых автоматом.

б) Какой
должна быть точность изготовления, чтобы процент годных деталей повысился до
98?

в)
Написать выражение для функции плотности вероятности и распределения случайной
величины.

Задача 13

Диаметр
детали, изготовленной цехом, является случайной величиной, распределенной по
нормальному закону. Дисперсия ее равна 0,0001 см, а математическое ожидание –
2,5 см. Найдите границы, симметричные относительно математического ожидания, в
которых с вероятностью 0,9973 заключен диаметр наудачу взятой детали. Какова
вероятность того, что в серии из 1000 испытаний размер диаметра двух деталей
выйдет за найденные границы?

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 14

Предприятие
производит детали, размер которых распределен по нормальному закону с
математическим ожиданием 20 см и стандартным отклонением 2 см. Деталь будет
забракована, если ее размер отклонится от среднего (математического ожидания)
более, чем на 2 стандартных отклонения. Наугад выбрали две детали. Какова вероятность
того, что хотя бы одна из них будет забракована?

Задача 15

Диаметры
деталей распределены по нормальному закону. Среднее значение диаметра равно d=14 мм
, среднее квадратическое
отклонение σ=2 мм
. Найти вероятность того,
что диаметр наудачу взятой детали будет больше α=15 мм и не меньше β=19 мм; вероятность того, что диаметр детали
отклонится от стандартной длины не более, чем на Δ=1,5 мм.

Задача 16

В
электропечи установлена термопара, показывающая температуру с некоторой
ошибкой, распределенной по нормальному закону с нулевым математическим
ожиданием и средним квадратическим отклонением σ=10℃. В момент когда термопара
покажет температуру не ниже 600℃, печь автоматически отключается. Найти
вероятность того, что печь отключается при температуре не превышающей 540℃ (то
есть ошибка будет не меньше 30℃).

Задача 17

Длина
детали представляет собой нормальную случайную величину с математическим
ожиданием 40 мм и среднеквадратическим отклонением 3 мм. Найти:

а)
Вероятность того, что длина взятой наугад детали будет больше 34 мм и меньше 43
мм;

б)
Вероятность того, что длина взятой наугад детали отклонится от ее
математического ожидания не более, чем на 1,5 мм.

Задача 18

Случайное
отклонение размера детали от номинала распределены нормально. Математическое
ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно
0,25 мм, стандартами считаются детали, размер которых заключен между 199,5 мм и
200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилась
и характеризуется средним квадратическим отклонением 0,4 мм. На сколько
повысился процент бракованных деталей?

Задача 19

Случайная
величина X~N(1,2²). Найти P{2

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 20

Заряд пороха для охотничьего ружья
должен составлять 2,3 г. Заряд отвешивается на весах, имеющих ошибку
взвешивания, распределенную по нормальному закону со средним квадратическим
отклонением, равным 0,2 г. Определить вероятность повреждения ружья, если максимально
допустимый вес заряда составляет 2,8 г.

Задача 21

Заряд
охотничьего пороха отвешивается на весах, имеющих среднеквадратическую ошибку
взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г. Определить
вероятность повреждения ружья, если максимально допустимый вес порохового
заряда 2,5 г.

Задача 21

Найти
вероятность попадания снарядов в интервал (α₁=10.7; α₂=11.2).
Если случайная величина X распределена по
нормальному закону с параметрами m=11;
σ=0.2.

Задача 22

Плотность
вероятности распределения случайной величины имеет вид

Найти
вероятность того, что из 3 независимых случайных величин, распределенных по
данному закону, 3 окажутся на интервале (-∞;5).

Задача 23

Непрерывная
случайная величина имеет нормальное распределение. Её математическое ожидание
равно 12, среднее квадратичное отклонение равно 2. Найти вероятность того, что
в результате испытания случайная величина примет значение в интервале (8,14)

Задача 24

Вероятность
попадания нормально распределенной случайной величины с математическим
ожиданием m=4 в интервал (3;5) равна 0,6. Найти дисперсию данной случайной
величины.

Задача 25

В
нормально распределенной совокупности 17% значений случайной величины X
меньше 13% и 47% значений случайной величины X
больше 19%. Найти параметры этой совокупности.

Задача 26

Студенты
мужского пола образовательного учреждения были обследованы на предмет
физических характеристик и обнаружили, что средний рост составляет 182 см, со
стандартным отклонением 6 см. Предполагая нормальное распределение для роста,
найдите вероятность того, что конкретный студент-мужчина имеет рост более 185
см.

Источник

Как найти математическое ожидание?

Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание — это первый начальный момент заданной СВ.

Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины — срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).

Нужна помощь? Решаем теорию вероятностей на отлично

Спасибо за ваши закладки и рекомендации

Формула среднего случайной величины

Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$

Пример нахождения математического ожидания

Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.

Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$

Используем формулу для м.о. дискретной случайной величины:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Получаем:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Вот в этом примере 2 описано также нахождение дисперсии Х.

Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.

Используем для нахождения мат. ожидания формулу:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Подставляем из условия плотность вероятности и вычисляем значение интеграла:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{1} 12(x^2-x^3) cdot x dx = int_{0}^{1} 12(x^3-x^4) dx = \
=left.(3x^4-frac{12}{5}x^5) right|_0^1=3-frac{12}{5} = frac{3}{5}=0.6.
$$

Другие задачи с решениями по ТВ

Подробно решим ваши задачи по теории вероятностей

Вычисление математического ожидания онлайн

Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.

Введите число значений случайной величины К.
Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
Нажмите на кнопку «Вычислить».
Калькулятор покажет вычисленное математическое ожидание $M(X)$.

Видео. Полезные ссылки

Видеоролики: что такое среднее (математическое ожидание)

Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).

Лучшее спасибо — порекомендовать эту страницу

Полезные ссылки

А теперь узнайте о том, как находить дисперсию или проверьте онлайн-калькулятор для вычисления математического ожидания, дисперсии и среднего квадратического отклонения дискретной случайной величины.

Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по терверу. Для закрепления материала — еще примеры решений по теории вероятностей.

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

Источник

Числовые характеристики распределения вероятностей. Математическое ожидание, дисперсия и стандартное отклонение

Закон распределения дискретной случайной величины
Математическое ожидание
Дисперсия
Среднее квадратичное отклонение
Правило трёх сигм
Примеры

п.1. Закон распределения дискретной случайной величины

Законом распределения дискретной случайной величины называют соответствие между полученными на опыте значениями этой величины X= {x_i} и их вероятностями p_i = P(x_i).
При этом сумма всех вероятностей равна 1: (mathrm{sum_{i=1}^n p_i=1})
Закон распределения можно задать таблицей, графиком или аналитически (в виде формулы).

Например:
Закон распределения случайной величины X = {0;1;2;3}, равной числу выпадения орлов при 3 бросках монеты, аналитически задаётся формулой: $$ mathrm{ p_i=P(x_i)=P_3(i)=frac{C_3^{i}}{2^3}, i={0;1;2;3} } $$

В табличном виде:

x_i	p_i
0	1/8
1	3/8
2	3/8
3	1/8

В виде графика:

п.2. Математическое ожидание

Математическое ожидание дискретной случайной величины X = {x_i} равно сумме произведений всех возможных значений x_i на соответствующие вероятности p_i: $$ mathrm{ M(X)=x_1p_1+x_2p_2+…+x_{n}p_{n}=sum_{i=1}^n x_{i}p_{i} } $$ Математическое ожидание является средним значением величины X.

Свойства математического ожидания
1) Размерность математического ожидания равна размерности случайной величины.
2) Математическое ожидание может быть любым действительным числом: положительным, равным 0, отрицательным.
3) Математическое ожидание постоянной величины равно этой постоянной:

M(C) = C

4) Математическое ожидание суммы независимых случайных величин равно сумме математических ожиданий:

M(X + Y) = M(X) + M(Y)

5) Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий:

M(XY) = M(X) · M(Y)

6) Постоянный множитель можно вынести за знак математического ожидания:

M(CX) = C · M(X)

Например:
Пусть в результате экспериментов получено следующее распределение случайной величины X – числа появления белых шаров (см. пример 1, §40 данного справочника):

Число белых шаров, x_i	0	1	2	3	4	5
p_i	(mathrm{C_5^0q^5})	(mathrm{C_5^1pq^4})	(mathrm{C_5^2p^2q^3})	(mathrm{C_5^3p^3q^2})	(mathrm{C_5^4p^4q})	(mathrm{C_5^5p^5})
0,0074	0,0618	0,2060	0,3433	0,2861	0,0954

Найдём математическое ожидание для данного распределения:

M(X) = 0 · 0,0074 + 1 · 0,0618 + … + 5 · 0,0954 = 3,125

п.3. Дисперсия

Дисперсия дискретной случайной величины X = {x_i} – это математическое ожидание квадрата отклонения случайной величины от её математического ожидания: $$ mathrm{ D(X)=M(X-M(X))^2 } $$ На практике дисперсия рассчитывается по формуле: $$ mathrm{ D(X)=M(X)^2-M^2(X)=sum_{i=1}^n x_i^2p_i-M^2(X) } $$

Свойства дисперсии
1) Размерность дисперсии равна квадрату размерности случайной величины.
2) Дисперсия может быть любым неотрицательным действительным числом.
3) Дисперсия постоянной величины равна нулю:

D(C) = 0

4) Дисперсия суммы независимых случайных величин равна сумме дисперсий:

D(X + Y) = D(X) + D(Y)

5) Постоянный множитель можно вынести за знак дисперсии:

D(CX) = C² · D(X)

Например:
Продолжим исследование и найдём дисперсию для распределения случайной величины X – числа появления белых шаров. Составим расчётную таблицу:

p_i

0,0074

0,0618

0,2060

0,3433

0,2861

0,0954

x_ip₁

0,0618

0,4120

1,0300

1,1444

0,4768

3,125

(mathrm{x_i^2})

–

(mathrm{x_i^2p_i})

0,0618

0,8240

3,0899

4,5776

2,3842

10,9375

Получаем: D(X) = 10,9375 – 3,125² ≈ 1,1719.

п.4. Среднее квадратичное отклонение

Среднее квадратичное отклонение (СКО) дискретной случайной величины X = {x_i} – это корень квадратный от дисперсии: $$ mathrm{ sigma(X)=sqrt{D(X)} } $$ СКО характеризует степень отклонения случайной величины от среднего значения.

Свойства СКО
1) Размерность СКО равна размерности случайной величины.
2) СКО может быть любым неотрицательным действительным числом.
3) СКО постоянной величины равно нулю:

σ(C) = 0

4) Постоянный множитель можно вынести за знак СКО:

σ(CX) = C · σ(X)

п.5. Правило трёх сигм

Большое количество случайных величин, измеряемых в экспериментах (например, в школьных лабораторных работах), имеет так называемое нормальное распределение.
В частности, при больших n, биномиальное распределение можно с хорошей точностью описывать как нормальное с M(X) = np и (mathrm{sigma(X)=sqrt{npq}}).
График плотности нормального распределения p(x) похож на колокол, с максимумом, соответствующим M(X) = X_cp – среднему значению измеряемой величины.

Величина СКО σ(X) характеризует степень отклонения X от среднего значения M(X).

Если величина X имеет нормальное распределение, то в пределах
±σ лежит 68,26% значений, принимаемых этой величиной
±2σ лежит 95,44% значений, принимаемых этой величиной
±3σ лежит 99,72% значений, принимаемых этой величиной
Вероятность того, что нормально распределённая величина примет значение, отклоняющееся от среднего больше, чем на «три сигмы», равна 0,28%, т.е. пренебрежимо мала.

п.6. Примеры

Пример 1. Найдите математическое ожидание, дисперсию и СКО при бросании кубика.

Закон распределения величины X – очки на верхней грани при бросании кубика и расчётная таблица:

p_i

1/6

x_ip₁

1/6

1/3

1/2

2/3

5/6

3,5

(mathrm{x_i^2})

–

(mathrm{x_i^2p_i})

(mathrm{frac16})

(mathrm{frac23})

(mathrm{1frac12})

(mathrm{2frac23})

(mathrm{4frac16})

(mathrm{15frac16})

Получаем: begin{gather*} mathrm{ M(X)=sum_{i=1}^6 x_ip_i=3,5 }\ mathrm{ D(X)=sum_{i=1}^6 x_i^2p_i-M^2(X)=15frac16-3,5^3=2frac{11}{12} }\ mathrm{ sigma(X)=sqrt{D(X)}=sqrt{2frac{11}{12}}approx 1,7 } end{gather*} Ответ: (mathrm{M(X)=3,5; D(X)=2frac{11}{12}; sigma(X)approx 1,7}).

Пример 2*. Найти математическое ожидание, дисперсию и СКО суммы очков при бросании двух кубиков.

Используем свойства мат.ожиданий и дисперсий.
Пусть X – очки на первом кубике, Y – на втором.
Параметры распределения для каждого из кубиков рассчитаны в примере 1.
(mathrm{M(X)=M(Y)=3,5, D(X)=D(Y)=2frac{11}{12}}).
Для суммы очков получаем:
(mathrm{M(X+Y)=M(X)+M(Y)=3,5+3,5=7})
(mathrm{D(X+Y)=D(X)+D(Y)=2frac{11}{12}+2frac{11}{12}=5frac56})
(mathrm{sigma(X+Y)=sqrt{D(X+Y)}=sqrt{5frac56}approx 2,4})
Ответ: (mathrm{M(X+Y)=7; D(X+Y)=5frac56; sigma(X+Y)approx 2,4}).

Пример 3*. Докажите, что в опытах по схеме Бернулли математическое ожидание M(X)=np, а дисперсия D(X)=npq.

Проведем один опыт. В нём может быть только два исхода: «успех» и «неудача».
Составим расчётную таблицу:

(mathrm{x_i^2p_i})

Мат.ожидание первого опыта (mathrm{M(X)=sum x_ip_i=p}).
Общее число успехов при n опытах складывается из числа успехов при каждом опыте, т.е. (mathrm{X=X_1+X_2+…+X_n}). Все опыты между собой независимы.
По свойству мат.ожидания суммы независимых событий: begin{gather*} mathrm{ M(X)=M(X_1+X_2+…+X_n)=M(X_1)+M(X_2)+…+M(X_n)= }\ mathrm{=underbrace{p+p+…+p}_{n text{раз}}=np } end{gather*} Дисперсия первого опыта (mathrm{D(X)=sum x_i^2p_i-M(X)=p-p^2=p(1-p)=pq})
По свойству дисперсии суммы независимых событий: begin{gather*} mathrm{ D(X)=D(X_1+X_2+…+X_n)=D(X_1)+D(X_2)+…+D(X_n)= }\ mathrm{=underbrace{pq+pq+…+pq}_{n text{раз}}=npq } end{gather*} Что и требовалось доказать.

Пример 4. 100 канцелярских кнопок высыпали на стул. Вероятность, что кнопка упала острием вверх, равна 0,4. Найдите среднее количество, дисперсию и СКО для числа кнопок, упавших острием вверх. Найдите интервал оценки для количества этих кнопок по правилу «трёх сигм».

По условию n = 100, p = 0,4.
Для каждой кнопки может быть два исхода: упасть острием вверх или вниз.
Таким образом, это испытание Бернулли с биномиальным распределением случайной величины. begin{gather*} mathrm{ M(X)=np=100cdot 0,4=40 }\ mathrm{D(X)=npq=100cdot 0,4cdot 0,6=24 }\ mathrm{sigma(X)=sqrt{D(X)}=sqrt{24}approx 4,9} end{gather*} Интервал оценки «три сигмы»: begin{gather*} mathrm{ M(X)-3sigma(X)lt Xlt M(X)+3sigma(X) }\ mathrm{40-3cdot 4,9lt Xlt 40+3cdot 4,9 }\ mathrm{25,3lt Xlt 54,7}\ mathrm{26leq Xleq 54} end{gather*} Скорее всего (99,7%), от 26 до 54 кнопок будут острием вверх.
Ответ: (mathrm{M(X)=40; D(X)=24; sigma(X)approx 4,9; 26leq Xleq 54})

Пример 5*. В тесте 10 задач с 4 вариантами ответов. Ответы выбираются наугад. Постройте распределение величины X = «количество угаданных ответов», найдите числовые характеристики этого распределения.
Найдите интервал оценки для количества угаданных ответов по правилу «трёх сигм».
Какова вероятность угадать хотя бы 1 ответ? Хотя бы 5 ответов? Угадать все 10 ответов?

По условию: (mathrm{n=10, p=frac14, q=frac34}).
Для каждого ответа может быть два исхода: «угадал»/ «не угадал».
Таким образом, это испытание Бернулли с биномиальным распределением случайной величины. $$ mathrm{ P_{10}(k)=C_{10}^kp^kq^{10-k}=C_{10}^kfrac{3^{10-k}}{4^{10}}=left(frac34right)^{10}frac{C_{10}^k}{3^k} } $$ Строим расчётную таблицу. Для (mathrm{C_{10}^k}) используем рекуррентную формулу (см. §36 данного справочника): $$ mathrm{ C_{n}^k=frac{n-k+1}{k}C_n^{k-1} } $$

(mathrm{x_i=k})	(mathrm{C_k})	(mathrm{3^k})	(mathrm{p_i(x_i)})	(mathrm{x_icdot p_i})	(mathrm{x_i^2})	(mathrm{x_i^2cdot p_i})
0	1	1	0,0563135	0,0000000	0	0,0000000
1	10	3	0,1877117	0,1877117	1	0,1877117
2	45	9	0,2815676	0,5631351	4	1,1262703
3	120	27	0,2502823	0,7508469	9	2,2525406
4	210	81	0,1459980	0,5839920	16	2,3359680
5	252	243	0,0583992	0,2919960	25	1,4599800
6	210	729	0,0162220	0,0973320	36	0,5839920
7	120	2187	0,0030899	0,0216293	49	0,1514053
8	45	6561	0,0003862	0,0030899	64	0,0247192
9	10	19683	0,0000286	0,0002575	81	0,0023174
10	1	59049	0,0000010	0,0000095	100	0,0000954
Σ			1	2,5		8,125

Получаем: begin{gather*} mathrm{ M(X)=sum_{i=0}^{10} x_ip_i=2,5 }\ mathrm{ D(X)=sum_{i=0}^{10} x_i^2p_i-M^2(X)=8,125=2,5^2=1,875 }\ mathrm{ sigma(X)=sqrt{D(X)}=sqrt{1,875}approx 1,37 } end{gather*}
Интервал оценки «три сигмы»: begin{gather*} mathrm{ M(X)-3sigma(X) lt Xlt M(X)+3sigma(X) }\ mathrm{ 2,5-3cdot 1,37lt X lt 2,5+3cdot 1,37 }\ mathrm{ -1,61lt Xlt 6,61 }\ mathrm{ 0leq Xleq 6 } end{gather*} Скорее всего (по расчетам – 99,65%), вы угадаете от 0 до 6 ответов.

Вероятность угадать хотя бы один ответ: begin{gather*} mathrm{ P(Xgeq 1)=1-p_0approx 1-0,0563=0,9437 }end{gather*} Очень хорошие шансы – 94,37%.
Вероятность угадать хотя бы 5 ответов: begin{gather*} mathrm{ P(Xgeq 5)=1-left(sum_{i=0}^{4}{p_i} right)approx 1-(0,0563+0,1877+…+0,1460)=0,0781 }end{gather*} Шансов мало – 7,81%. Т.е. «средний балл» при сдаче тестов мало достижим методом научного тыка.
Вероятность угадать все 10 ответов: p₁₀≈ 0,000001. Шанс – один из миллиона.

Источник

Содержание:

Примеры с решением
Нормальное распределение и его числовые характеристики
Логарифмически-нормальное распределение

Нормальное распределение является наиболее распространенным типом распределения, предполагаемым в техническом анализе фондового рынка и в других видах статистического анализа. Стандартное нормальное распределение имеет два параметра: среднее значение и стандартное отклонение . Для нормального распределения 68% наблюдений находятся в пределах +/- одно стандартное отклонение от среднего значения, 95% находятся в пределах +/- два стандартных отклонения, а 99,7% находятся в пределах + — три стандартных отклонения.

Определение:

Общим нормальным распределением вероя тностей непрерывной случайной величины называется распределение с плотностью

Нормальное распределение задается двумя параметрами: и .

По определениям математического ожидания и дисперсии после выполнения соответствующих интегрирований можно вывести, что для нормального распределения справедливы формулы:

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Определение:

Нормальное распределение с параметрами и называется нормированным; его плотность

Поскольку функция является четной, неопределенный интеграл от нее — нечетная функция, и потому вместо функции распределения используется функция Лапласа Функции табулированы Графики плотности нормального распределения для разных значений показаны на рис. 2.6.

Пусть случайная величина X задана плотностью нормального распределения ; тогда вероятность того, что примет значение на интервале согласно формулам равна: Преобразование этой формулы путем введения новой переменной интегрирования приводит к удобной вычислительной формуле где — функция Лапласа, определенная по формуле.

Возможно вам будут полезны данные страницы:

Модель нормального распределения мотивирована центральной предельной теоремой.

Теория утверждает, что средние значения, рассчитанные из независимых идентично распределенных случайных величин, имеют приблизительно нормальные распределения, независимо от типа распределения, из которого выбираются переменные (при условии, что они имеют конечную дисперсию). Нормальное распределение иногда путают с симметричным распределением. Симметричное распределение — это то, где разделительная линия создает два зеркальных изображения, но фактические данные могут быть двумя горбами или серией холмов в дополнение к кривой колокола, которая указывает на нормальное распределение.

Примеры с решением

Пример 1.

Случайная величина распределена по нормальному закону с математическим ожиданием и средним квадратическим отклонением, соответственно равными 10 и 5. Найти вероятность того, что примет значение на интервале (20, 30).

Решение:

Воспользуемся формулой . По условию Следовательно, По табл. 2 приложения находим соответствующие значения функции Лапласа и окончательно получаем:

Пример 2.

Магазин продает мужские костюмы. По данным статистики, распределение по размерам является нормальным с математическим ожиданием и средним квадратическим отклонением, соответственно равным 48 и 2. Определить процент спроса на костюмы 50-го размера при условии разброса значений этого размера в интервале (49, 51).

Решение:

По условию задачи Используя формулу (2.66), получаем, что вероятность спроса на костюмы 50-го размера в заданном интервале равна:

Следовательно, спрос на костюмы 50-го размера составит около 24%, и магазину нужно предусмотреть это в общем объеме закупки.

Нормальное распределение и его числовые характеристики

ДСВ — дискретная случайная величина

НСВ — непрерывная случайная величина.

В этом подразделе мы создадим функцию распределения для каждого типа НСВ и создадим график, выясним числовые свойства этого типа НСВ и узнаем тип НСВ в реальных ситуациях из содержания задачи. вы будете учиться. Наиболее распространенным в природе, экономике, социологии и других науках является нормальное распределение непрерывных случайных величин.

Используя нормальное распределение, вы можете описать плотность вероятности НСВ, когда появляются отклонения от среднего случайного значения из-за различных явлений, действующих независимо друг от друга, но в одинаковой степени.

Чем больше случайных случайных величин добавлено, тем точнее результат. Все эти явления не зависят друг от друга, но, воздействуя на процесс изготовления примерно с одинаковой силой, обусловливают то, что закон, по которому изменяется НСВ (например, размер конкретной детали), описывается нормальным распределением.

Самое точное изготовление детали с заданными размерами — «эталон» — будет соответствовать математическому ожиданию т, разброс фактических значений случайной величины размера детали — понятию дисперсии (точнее — среднеквадратическому отклонению ). Случайная величина с нормальным распределением существует в интервале и описывается законами: плотности вероятности называемой «кривой Гаусса» (рис. 2.9, а) где и — параметры нормального распределения, причем функции распределения (рис. 2.9, б):

Рис. 2.9

Подстановкой интеграл приводится к виду

Поэтому для удобства вводится нечетная функция называемая функцией Лапласа. Функцию Лапласа называют также «интегралом вероятности», или «функцией ошибок». Очевидно, что

Математическое ожидание случайной величины распределенной нормааьно, равно дисперсия равна поэтому параметр — среднеквадратическое отклонение.

Случайную величину распределенную нормально с параметрами и обозначают На практике для вычисления значений функции Лапласа используются таблицы, которые приводятся в справочной литературе (табл. П. 3). Вероятность попадания в интервал НСВ, распределенной по нормальному закону, можно найти с помощью функции Лапласа по формуле

Величины параметров нормального распределения СВ непосредственно влияют на форму кривой при она принимает максимальное значение, равное Поэтому с увесил личением (уменьшением) максимальная ордината убывает (возрастает) и кривая становится более пологой, приближаясь к оси

Величина математического ожидания влияет на расположение кривой относительно оси ординат: при возрастании (убывании) кривая смещается вправо (влево). Поэтому с помощью подстановки можно получить функцию плотности вероятности, график которой симметричен относительно оси Такая кривая соответствует нормированному закону нормального распределения с параметрами и Величину называют стандартно нормальной. Ее функция распределения имеет вид

Логарифмически-нормальное распределение

Определение. Непрерывная случайная величина имеет логарифмически-нормальное (сокращенно логнормальное распределение), если ее логарифм подчинен нормальному закону. Так как при неравенства равносильны, то функция распределения логнормального распределения совпадает с функцией нормального распределения для случайной величины т.е. в соответствии с

Дифференцируя по получим выражение плотности вероятности для логнормального распределения

(рис. 4.14).

Можно доказать, что числовые характеристики случайной величины распределенной по логнормальному закону, имеют вид: математическое ожидание дисперсия мода медиана Очевидно, чем меньше тем ближе друг к другу значения моды, медианы и математического ожидания, а кривая распределения — ближе к симметрии.

Если в нормальном законе параметр а выступает в качестве среднего значения случайной величины, то в логнормальном — в качестве медианы. Логнормальное распределение используется для описания распределения доходов, банковских вкладов, цен активов, месячной заработной платы, посевных площадей под разные культуры, долговечности изделий в режиме износа и старения и др.

Нормальное распределение, также известное как распределение Гаусса, является распределением вероятностей , симметричным относительно среднего значения, показывающим, что данные около среднего значения встречаются чаще, чем данные, далекие от среднего значения.

Пример 3.

Проведенное исследование показало, что вклады населения в данном банке могут быть описаны случайной величиной распределенной по логнормальному закону с параметрами Найти: а) средний размер вклада; б) долю вкладчиков, размер вклада которых составляет не менее 1000 ден. ед.; в) моду и медиану случайной величины и пояснить их смысл.

Решение:

а) Найдем средний размер вклада, т.е.

б) Доля вкладчиков, размер вклада которых составляет не менее 1000 ден. ед., есть

При определении воспользуемся тем, что функция логнормального распределения случайной величины совпадает с функцией нормального распределения случайной величины т.е. с учетом имеем:

Теперь

(рис. 4.15).

в) Вычислим моду случайной величины т.е. наиболее часто встречающийся банковский вклад равен 280 ден. ед. (точнее, наиболее часто встречающийся элементарный интервал с центром 280 ден. ед., т.е. интервал ( Если исходить из вероятностного смысла параметра логнормального распределения, то медиана т.е. половина вкладчиков имеют вклады до 530 ден. ед., а другая половина — сверх 530 ден. ед.