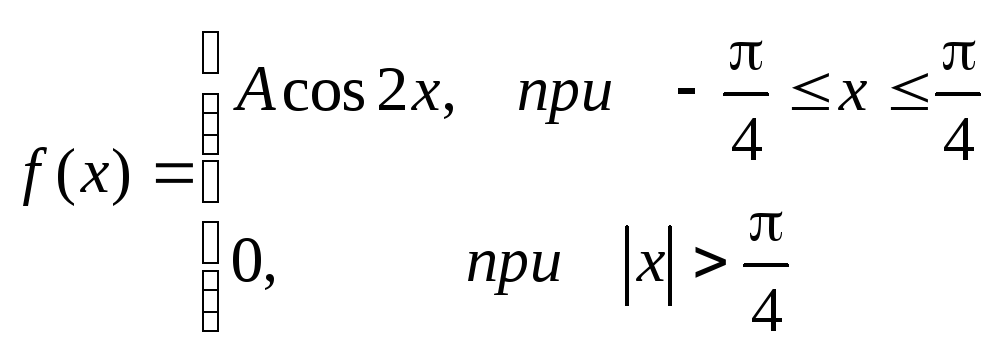Как найти матем ожидание - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти математическое ожидание?

Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание — это первый начальный момент заданной СВ.

Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины — срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).

Нужна помощь? Решаем теорию вероятностей на отлично

Полезная страница? Сохрани или расскажи друзьям

Формула среднего случайной величины

Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$

Пример нахождения математического ожидания

Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.

Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$

Используем формулу для м.о. дискретной случайной величины:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Получаем:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Вот в этом примере 2 описано также нахождение дисперсии Х.

Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.

Используем для нахождения мат. ожидания формулу:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Подставляем из условия плотность вероятности и вычисляем значение интеграла:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{1} 12(x^2-x^3) cdot x dx = int_{0}^{1} 12(x^3-x^4) dx = \
=left.(3x^4-frac{12}{5}x^5) right|_0^1=3-frac{12}{5} = frac{3}{5}=0.6.
$$

Другие задачи с решениями по ТВ

Подробно решим ваши задачи по теории вероятностей

Вычисление математического ожидания онлайн

Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.

Введите число значений случайной величины К.
Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
Нажмите на кнопку «Вычислить».
Калькулятор покажет вычисленное математическое ожидание $M(X)$.

Видео. Полезные ссылки

Видеоролики: что такое среднее (математическое ожидание)

Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).

Лучшее спасибо — порекомендовать эту страницу

Полезные ссылки

А теперь узнайте о том, как находить дисперсию или проверьте онлайн-калькулятор для вычисления математического ожидания, дисперсии и среднего квадратического отклонения дискретной случайной величины.

Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по терверу. Для закрепления материала — еще примеры решений по теории вероятностей.

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

Источник

Математическое ожидание — это ожидаемый результат от какого-то действия.

Например, можно рассчитать ожидаемую стоимость инвестиции в определённый момент в будущем. Рассчитывая математическое ожидание перед тем, как инвестировать, можно выбрать наилучший сценарий который, по мнению инвестора, даст наилучший результат.

Случайная величина может быть двух типов:

Дискретной: число возможных значений X — это числимое конечное или бесконечное множество точек; пример: количество дефектных устройств в производстве фабрики.
Непрерывной: X может принимать любое значение в заданном диапазоне; пример: концентрация углекислого газа в воде.

Математическое ожидание дискретной случайной величины рассчитывается этой формулой:

Математическое ожидание дискретной случайной величины рассчитать формула: M(X)=∑ Xi×Pi

M(X) = ∑ xi × pi
Где:
М — математическое ожидание,
X — случайная величина,
p — вероятность появления случайной величины.

Математическое ожидание дискретной случайной величины рассчитывается:
1. Сначала нужно умножить каждое из возможных результатов на свою вероятность (например: вероятность, что выпадет «1» — 1/6, «2» — 1/3, значит умножаем 1 на 1/6, 2 на 1/3, и т.д.),
2. Затем суммируем все эти значения (1 × 1/6 + 2 × 1/3 и т.д.).

Для непрерывной случайной величины используется эта формула:

Математическое ожидание непрерывной случайной величины рассчитать формула: M(X) = -∞+∞f(x) × x.dx

M(X) = ∫ f(x) × x.dx
Где:
М — математическое ожидание
f (x) — функция (которая будет предоставлена в условии задачи)
x — случайная величина
dx — элемент интегрирования

В этом случае рассчитывается интеграл в заданном интервале.

Примеры вычисления математического ожидания

Кратко:

если в задаче даётся таблица с данными, то перемножаем каждое событие на его вероятность и потом всё складываем;
если в задаче дают функцию с заданным интервалом, то вычисляем интеграл с этим интервалом.

Пример 1

Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:

xi	−1	1	2	3	4
pi	0,1	0,2	0,3	0,1	0,3

Используется формула для дискретной случайной величины:

M(X) = ∑ xi×pi = −1×0,1+ 1×0,2 + 2×0,3 + 3×0,1 + 4×0,3 = −0,1 + 0,2 + 0,6 + 0,3 + 1,2 = 2,2

Пример 2

Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = 2x, при x∈(0,1) и f(x) = 0 в остальных точках.

Используется формула для непрерывной случайной величины:

Пример 3

Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:

xi	1	2	3	4	5
pi	0,3	0,3	0,1	0,1	0,2

Используется формула для дискретной случайной величины:

M(X) = ∑ xi×pi = 1×0,3 + 2×0,3 + 3×0,1 + 4×0,1 + 5×0,2 = 0,3 + 0,6 + 0,3 + 0,4 + 1 = 2,6

Пример 4

Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = (1/10).(3x²+1), при x∈(0,2) и f(x) = 0 в остальных точках.

Используется формула для непрерывной случайной величины:

Узнайте больше про Интегралы.

Основные свойства математического ожидания

Математическое ожидание постоянной равно самой постоянной: М(c)=c.
Математическое ожидание сложения/вычитания двух случайных величин равно сумме/вычитанию их математических ожиданий: пусть X и Y — две случайные величины, значит М (X ± Y) = М (X) ± М (Y).
Если умножить случайную величину X на c, её среднее значение также умножается на эту константу (c): М (cX) = cМ (X).
Если добавить или вычесть c из случайной величины X, то произойдёт та же операция (сложение или вычитание константы) с её средним значением: М (X ± c) = М (X) ± c.
Если X и Y — две независимые случайные величины, значит: М(XY)=М(X)×М(Y).

Узнайте больше про Теорию вероятностей.

Источник

22
Апр 2019

Теория вероятностей

Математическое ожидание

Математическое ожидание.

В этой статье мы рассмотрим определение и свойства математического ожидания, а также рассмотрим примеры решения задач.

Рассмотрим некоторую случайную величину , которая может принимать числовые значения

Пусть распределение вероятностей случайной величины задано таблицей:

Математическим ожиданием случайной величины называют число

Математическое ожидание называют также ожидаемым значением случайной величины , средним значением случайной величины .

Свойства математического ожидания.

Свойство 1. Пусть — случайная величина, — некоторое число. Рассмотрим случайную величину . Тогда

Свойство 2. Пусть и — две случайные величины. Тогда — тоже случайная величина, и при этом:

Это значит, что математическое ожидание суммы случайных величин равно сумме их математических ожиданий.

Свойство 3. Если случайная величина принимает значения с одинаковой вероятностью, то

Это значит, что если все значения случайной величины равновероятны, то математическое ожидание равно среднему арифметическому числовых значений случайной величины .

Пример 1. Страховой полис КАСКО в страховой компании стоит 35 000 рублей. По статистике в течение года владелец автомобиля попадает в мелкую аварию с вероятностью 0,18, и средняя сумма страховой выплаты при этом равна 50 000 рублей. С вероятностью 0,034 автомобилист попадает в серьезную аварию, и средняя сумма выплаты при этом 700 000 рублей. Найдите

Математическое ожидание случайной величины «средняя сумма страховой выплаты»
Математическое ожидание случайной величины «средний доход страховой компании от продажи одного полиса»

Решение. показать

Пример 2. Случайная величина задана распределением:

Сколько значений принимает случайная величина ?
Найдите математическое ожидание случайной величины .

Решение. показать

Пример 3. В торговом центре установлены два автомата, продающие кофе. С вероятностью к вечеру в первом автомате заканчивается кофе. Во втором автомате кофе заканчивается к вечеру с вероятностью . Найдите математическое ожидание числа автоматов, в которых к вечеру закончится кофе.

Решение. показать

Пример 4. Баскетболист попадает в корзину с вероятностью . Найдите математическое ожидание числа попаданий при 50 бросках.

Решение. показать

Пример 5. Василий пытается отправить СМС в условиях слабой мобильной связи. Телефон делает попытки отправить СМС до тех пор, пока это не удастся. Известно, что вероятность удачной попытки равна независимо от предыдущих попыток. Найдите математическое ожидание числа сделанных попыток.

Решение. показать

Пример 6. Найдите математическое ожидание случайной величины «число неудач» в серии из 16 испытаний Бернулли с вероятностью успеха в одном испытании.

Решение. показать

Пример 7. Найдите математическое ожидание случайной величины «число очков, выпавших на игральной кости».

Решение. показать

Пример 8. Игральную кость бросают 5 раз. Найдите математическое ожидание суммы выпавших очков.

Решение. показать

Репетитор по математике И.В. Фельдман

Источник

Математическое ожидание, дисперсия, среднее квадратичное отклонение

Эти величины определяют некоторое
среднее значение, вокруг которого
группируются значения случайной
величины, и степень их разбросанности
вокруг этого среднего значения.

Математическое ожидание Mдискретной случайной величины — это
среднее значение случайной величины,
равное сумме произведений всех возможных
значений случайной величины на их
вероятности.

Свойства математического ожидания:

Математическое ожидание постоянной
величины равно самой постоянной .
Постоянный множитель можно выносить
за знак математического ожидания .
Математическое ожидание произведения
двух независимых случайных величин
равно произведению их математических
ожиданий .
Математическое ожидание суммы двух
случайных величин равно сумме
математических ожиданий слагаемых

Для описания многих практически важных
свойств случайной величины необходимо
знание не только ее математического
ожидания, но и отклонения возможных ее
значений от среднего значения.

Дисперсия случайной величины— мера разброса случайной величины,
равная математическому ожиданию квадрата
отклонения случайной величины от ее
математического ожидания.

Принимая во внимание свойства
математического ожидания, легко показать
что

Казалось бы естественным рассматривать
не квадрат отклонения случайной величины
от ее математического ожидания, а просто
отклонение. Однако математическое
ожидание этого отклонения равно нулю.
Это объясняется тем, что одни возможные
отклонения положительны, другие
отрицательны, и в результате их взаимного
погашения получается ноль. Можно было
бы принять за меру рассеяния математическое
ожидание модуля отклонения случайной
величины от ее математического ожидания,
но как правило, действия связанные с
абсолютными величинами, приводят к
громоздким вычислениям.

Свойства дисперсии:

Дисперсия постоянной равна нулю.
Постоянный множитель можно выносить
за знак дисперсии, возводя его в квадрат.
Если x и y независимые случайные величины
, то дисперсия суммы этих величин равна
сумме их дисперсий.

Средним квадратическим отклонением
случайной величины(иногда применяется
термин «стандартное отклонение случайной
величины») называется число равное.

Среднее квадратическое отклонение,
является, как и дисперсия, мерой рассеяния
распределения, но измеряется, в отличие
от дисперсии, в тех же единицах, которые
используют для измерения значений
случайной величины.

Решение задач:

1)Дана случайная величина Х:

x_i	-3	-2	0	1	2
p_i	0,1	0,2	0,05	0,3	0,35

Найти М(х), D(X).

Решение:

=9=2,31.

2) Известно, что М(Х)=5, М(Y)=2.
Найти математическое ожидание случайной
величиныZ=6X-2Y+9-XY.

Решение:М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25.

Пример:Известно, чтоD(Х)=5,D(Y)=2. Найти
математическое ожидание случайной
величиныZ=6X-2Y+9.

Решение:D(Z)=6²D(Х)-2²D(Y)+0=180-8=172.

Тема 7. Непрерывные случайные величины

Задача 14

Случайная
величина, значения которой заполняют
некоторый промежуток, называется
непрерывной.

Плотностью распределениявероятностей непрерывной случайной
величины Х называется функцияf(x)– первая производная от функции
распределенияF(x).

Плотность
распределения также называют
дифференциальной
функцией.
Для описания дискретной случайной
величины плотность распределения
неприемлема.

Зная плотность распределения, можно
вычислить вероятность того, что некоторая
случайная величина Х примет значение,
принадлежащее заданному интервалу.

Вероятность того, что непрерывная
случайная величина Х примет значение,
принадлежащее интервалу (a,
b), равна определенному
интегралу от плотности распределения,
взятому в пределах от a
до b.

Функция распределения может быть легко
найдена, если известна плотность
распределения, по формуле:

Свойства плотности распределения.

1) Плотность распределения – неотрицательная
функция.

2) Несобственный интеграл
от плотности распределения в пределах
от -доравен единице.

Решение задач.

1.Случайная величина подчинена
закону распределения с плотностью:

Требуется найти коэффициент а,
определить вероятность того, что
случайная величина попадет в интервал
от 0 до.

Решение:

Для нахождения коэффициента авоспользуемся свойством.

2 .Задана непрерывная случайная
величинахсвоей функцией распределенияf(x).

Требуется определить
коэффициент А, найти функцию распределения,
определить вероятность того, что
случайная величинахпопадет в
интервал.

Решение:

Найдем коэффициент А.

Найдем функцию распределения:

1) На участке
:

2) На участке

3) На участке

Итого:

Найдем вероятность попадания случайной
величины в интервал
.

Ту же самую вероятность можно искать
и другим способом:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость

Математическое ожидание

Чтобы определить такое понятие как математическое ожидание, представим себе некую случайную величину, которая имеет значения $ X_1, X_2 … X_n$. Каждое из значений может приниматься с определённой вероятностью. То есть каждому конкретному значению, соответствует своя вероятность и в целом они составляют ряд $ P_1, P_2 … P_n$

Определение 1

Вычислить математическое ожидание дискретной случайной величины можно сложив числа, полученные умножением каждого значения величины на вероятность, соответствующую ей.

$M(X)= X_1cdot P_1 + X_2cdot P_2 + … + X_ncdot P_n$

Пример 1

Организован розыгрыш, в котором за каждый билет полагается приз. Всего есть 1000 билетов, призы в которых распределены следующим образом:

50 рублей — 300 призов
75 рублей — 200 призов
100 рублей — 200 призов
200 рублей — 150 призов
400 рублей — 100 призов
600 рублей — 50 призов

Какова величина среднего приза, который может быть получен по одному билету?

Решение

Вычислим средний выигрыш, который можно получить по билету как среднее арифметическое от всех выигрышей.

$ frac {50 cdot 300 + 75 cdot 200 + 100 cdot 200 + 200 cdot 150 + 400 cdot 100 + 600 cdot 50}{1000} = 150 $

Среднее арифметическое получается 150 рублей можно в среднем выиграть приобретя один билет. Интересно, что математически расчёт проводится практически точно так же, как вычисляется и математическое ожидание, ведь приведённое выше выражение можно представить в виде:

$ frac { 50 cdot 300}{1000} + frac { 75 cdot 200}{1000} + frac { 100 cdot 200}{1000} + frac { 200 cdot 150}{1000} + frac { 400 cdot 100}{1000} + frac { 600 cdot 50 }{1000}= 50 cdot frac { 300}{1000} + 75 cdot frac { 200}{1000} + 100 cdot frac { 200}{1000} + 200 cdot frac { 150}{1000} + 400 cdot frac { 100}{1000} + 600 cdot frac { 50 }{1000} $

И каждый из элементов $frac { 300}{1000}$, $ frac { 200}{1000}$, $ frac { 200}{1000}$, $ frac { 150}{1000}$, $ frac { 100}{1000}$, $ frac { 50 }{1000} $ соответствует вероятности, получить тот или иной приз. Таким образом, математическое ожидание приза, как случайной величины, имеет смысл среднего, наиболее вероятного, выигрыша.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример 2

Владелец завода решил выпускать новую продукцию. Рыночная цена нового изделия составит 300 рублей. Из этой суммы он получит 150 рублей, 100 рублей получит магазин, 50 рублей получат рабочие, которые трудятся на заводе. При этом, так как изделие новое, то неизвестно точно, сколько экземпляров удастся продать за конечный промежуток времени, например месяц. Есть только прогноз, что с определённой вероятностью будет продано некое определённое количество изделий:

500 штук будет продано с вероятностью 0,2, затраты на производство, не считая зарплаты рабочих, составят 100000;
1000 штук будет продано с вероятностью 0,4, затраты 150000;
2000 штук будет продано с вероятностью 0,25, затраты 200000;
3000 штук будет продано с вероятностью 0,10, затраты 250000;
4000 штук будет продано с вероятностью 0,05, затраты 300000;

Требуется вычислить прибыль, которую получит владелец завода.

Решение

Согласно условию «прибыль» является случайной величиной, так как она зависит от другой случайной величины — количества проданных изделий. Рассчитаем прибыль и математическое ожидание:

500 штук, прибыль $500 cdot 150 – 100 000=-25000$ вероятность 0,2;
1000 штук, прибыль $1000 cdot 150 – 150 000=0$ вероятность 0,4;
2000 штук, прибыль $2000 cdot 150 – 200 000=100 000$ вероятность 0,25;
3000 штук прибыль $3000 cdot 150 – 250 000=200 000$ вероятность 0,10;
4000 штук, прибыль $4000 cdot 150 – 300 000=300 000$ вероятность 0,05;

По полученным данным, рассчитаем математическое ожидание, согласно формуле из определения:

$M(X)= -25000cdot 0,2 + 0 cdot 0,4 + 100 000 cdot 0,25 + 200 000 cdot 0,10 + 300 000 cdot 0,05 = 55 000$

В результате получили, что математическое ожидание, которое характеризует среднюю ожидаемую прибыль в долгосрочной перспективе, составит 55 000 рублей.

Свойства математического ожидания

Свойство 1

Матожидание взятое от константы, то есть величины постоянной, будет равно самой этой же величине.

$E(C)=C$

Свойство 2

Если берётся матожидание от случайной величины умноженной на постоянную, то данную постоянную можно вынести за обозначение матожидания.

$E(CX)=Cdot E(X)$

Свойство 3

Матожидание от сложения или вычитания двух независимых случайных величин, можно представить как сложение или вычитание самих матожиданий от этих величин, взятых по отдельности.

$E(Xpm Y)=E(X) pm E(Y)$

Свойство 4

Если берётся матожидание от двух случайных величин умноженных друг на друга, то его можно представить как умноженные друг на друга математические ожидания от данных величин взятые по отдельности.

$E(Xcdot Y)=E(X) cdot E(Y)$

Свойство 5

Матожидание от суммы или разности случайной величины и константы, постоянной величины, можно представить в виде суммы или разности самого матожидания от случайной величины и этой же константы.

$E(Xpm С)=E(X) pm С $

Пример 3

Имеется три ёмкости заполненные белыми и чёрными шарами. Вероятность достать чёрный шар из первой ёмкости (событие $X_1$) составляет $P_1=0,4$, из второй ёмкости (событие $X_2$) $P_2=0,3$, из третьей ёмкости (событие $X_2$) $P_3=0,6$. Требуется рассчитать матожидание события X, при котором из всех ёмкостей будут вынуты только чёрные шары.

Решение

Событие заключающееся в том, что из ёмкости вынут чёрный шар является случайной величиной, которая может принимать исключительно два значения 1, если вынут чёрный шар, и 0, если вынут шар другого цвета. Поэтому математические ожидания от выполнения событий $X_1, X_2, X_3$ составят величины равные вероятностям данных событий. То есть

$M(X_1)=P_1=0,4$;

$M(X_2)=P_2=0,3$;

$M(X_3)=P_3=0,6$;

Событие состоящее в том, что из всех трёх ёмкостей вынуты только чёрные шары, тоже является случайной величиной и представляет собой сумму событий $X_1, X_2, X_3$:

$ X=X_1+ X_2+ X_3$

Значит можно записать:

$ M(X)=M(X_1+ X_2+ X_3)$

Согласно третьему свойству матожидания выражение примет вид:

$ M(X)=M(X_1+ X_2+ X_3)=M(X_1)+M( X_2)+ M(X_3)= 0,4+0,3+0,6=1,3$

Таким образом, математическое ожидание события X составляет 1,3.

Не получается написать работу самому?

Доверь это кандидату наук!

Источник