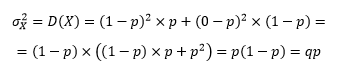Биномиальное распределение, его математическое ожидание, дисперсия
Рассмотрим
серию независимых
испытаний проведенных в условиях схемы
Бернулли, в ходе которых появлялось
событиес вероятностью
,
одинаковой для всех испытаний.
Необходимо
определить закон распределения случайной
величины
числа появлений события
.
Для этого нужно определить возможные
значенияи их вероятности. Минимальное значение
равно нулю, что соответствует ситуации,
когда в сериииспытаний событие
не появилось; максимальное значение
соответствует «успеху» во всех испытаниях
серии и равно.
Очевидно, что случайная величиначисла появлений события
в серии
испытаний принимает значения
.
Остается найти соответствующие
вероятности этих возможных значений,
для чего достаточно воспользоваться
формулой Бернулли:
,
где
,
.
Эта
формула является аналитическим выражением
искомого закона распределения. Эта
формула еще называется биномиальной,
так как ее правая часть представляет
собой
-й
член бинома Ньютона:
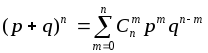
Отсюда
сразу видно, что для полученного закона
биномиального распределения вероятностей
числа появления события
при
независимых испытаниях выполняется
условие нормировки, т.е. сумма всех
вероятностей равна единице:
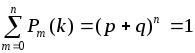
Теорема.
Математическое
ожидание числа появлений события
в
независимых испытаниях равно произведению
числа испытаний на вероятность появления
событияв каждом испытании.
Доказательство.
Случайная величина
распределена по биномиальному закону:
(
),
где
.
Величину
можно рассматривать, как сумму независимых
случайных величин,
где(
)
– число появлений событияв
м
испытании. Случайная величинапринимает лишь два значения: 1, если
событиепоявилось в
м
испытании, и 0, если вм
испытании событияне произошло.
Вероятности
этих событий
и
,
а математическое ожидание:(
).
Следовательно,
используя теорему о математическом
ожидании суммы, получим:
.
Таким
образом, математическое ожидание числа
появлений события
в условиях схемы Бернулли совпадает со
средним числом появлений событияв данной серии испытаний.
Теорема.
Дисперсия
числа появлений события
в
независимых испытаниях равна произведению
числа испытаний на вероятности появления
и непоявления событияв одном испытании:
.
Доказательство.
Пусть
– число появлений события
в
независимых испытаниях. Оно равно сумме
появлений событияв каждом испытании:
.
Так как испытания независимы, то и
случайные величины– независимы, поэтому
.
Но
,
.
Как
было показано выше,
,
а.
Тогда
,
а.
В
этом случае, как уже упоминалось ранее,
среднее квадратичное отклонение
.
Пример.
В пяти торговых точках проверяется
годовой баланс. Вероятность правильного
оформления баланса в каждой точке равна
0,7. Найти математическое ожидание и
дисперсию правильно оформленных
балансов.
Решение.
Дано:
,
,
.
Тогда
.
Биномиальный
закон распределения часть приходится
применять в условиях, когда число
независимых испытаний велико. Вычисление
вероятностей по формуле Бернулли при
этом усложняется, поэтому представляет
интерес асимптотическое приближение
для биномиального закона, справедливое
при больших
.
Возможны два случая:
-
Когда
при увеличении числа испытаний
математическое ожидание рассматриваемой
случайной величины
тоже неограниченно возрастает (случай
постоянного);
при этом биномиальное распределение
сходится к нормальному закону, который
будет рассмотрен позже. -
Когда
при увеличении числа испытаний остается
постоянным произведение
,
то есть математическое ожидание
рассматриваемой случайной величины
остается конечным. Это означает, что
вероятность событиястремится к нулю. В этом случае
биномиальное распределение сходится
к распределению Пуассона.
Распределение
пуассона
Рассмотрим
второй случай асимптотического
приближения биномиального распределения,
когда
,
а– имеет конечное значение. Случайная
величинаназываетсяраспределенной
по закону Пуассона
с параметром
,
если эта случайная величина может
принимать значения,
соответствующая вероятность которых
определяется по формуле Пуассона, когда:
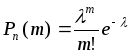
В
биномиальном распределении величина
имеет смысл математического ожидания.
Проведем вычисления математического
ожидания для распределения Пуассона:
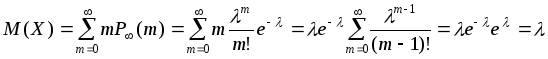
Таким
образом, в распределении Пуассона
величина
также имеет смысл математического
ожидания.
Проведем
вычисления дисперсии для распределения
Пуассона:
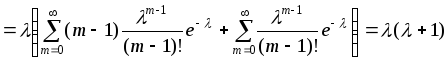
поскольку

Таким
образом, в распределении Пуассона
дисперсия также равна
.
Нормальное
распределение
Нормальным
называется такое распределение случайной
величины
,
плотность вероятности которого
описывается функцией Гаусса:
где
– среднее квадратичное отклонение;
– математическое ожидание случайной
величины.
Свойства
функции Гаусса
График
плотности нормального распределения
называют нормальной
кривой Гаусса.
Проведем
исследование функции:
методами
дифференциального исчисления.
-
Очевидно,
что функция определена на всей оси
.
-
При
всех значениях
функция принимает положительные
значения, т.е. нормальная кривая
расположена над осью.
-
Ось
служит горизонтальной асимптотой
графика, поскольку.
Других асимптот у графика нет. -
При
функция имеет максимум, равный
.
-
Функция
четная: ее график симметричен относительно
прямой
.
-
При
график функции имеет точки перегиба.
Изменение
величины математического ожидания,
т.е. параметра
,
ведет к сдвигу кривой вдоль осибез изменения ее формы. График ведет
себя иначе, если изменяется среднее
квадратичное отклонение (параметр):
с возрастаниеммаксимальная ордината нормальной кривой
убывает, а сама кривая становится более
пологой, т.е. сжимается к оси;
при убываниинормальная кривая становится более
островершинной и растягивается в
положительном направлении оси.
Нопри
любых значениях параметров
и
,
согласно условию нормировки функции
плотности распределения, площадь,
ограниченная нормальной кривой и осьюостается равной единице.
Схема
независимых испытаний Бернулли
Серия
повторных независимых испытаний, в
каждом из которых данное событие
имеет одну и ту же вероятность
,
не зависящую от номера испытания,
называетсясхемой
Бернулли.
Таким образом, в схеме Бернулли для
каждого испытания имеются только два
исхода: событие
(успех), вероятность которого
и событие
(неудача), вероятность которого
.
Рассмотрим
задачу:
в
условиях схемы Бернулли необходимо
определить вероятность того, что при
проведении
независимых испытаний, в
испытаниях наступит событие
,
если вероятность его наступления в
каждом испытании равна.
Определим
вначале вероятность того, что в первых
испытаниях событие
наступит, а в остальных
испытаниях не наступит. Вероятность
такого события можно получить по формуле
вероятности произведения независимых
событий,
где.
Это
лишь одна из возможных комбинаций, когда
событие
произошло только в первых
испытаниях. Для определения искомой
вероятности нужно перебрать все возможные
комбинации. Их число равно числу сочетаний
изэлементов по
,
т.е.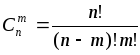
Таким
образом, вероятность того, что событие
наступит в любых
испытаниях, определяется поформуле
Бернулли:
.
Наивероятнейшее
число наступления событий в схеме
Бернулли
Число
наступлений события
называетсянаивероятнейшим,
если оно имеет наибольшую вероятность
по сравнению с вероятностями наступления
любое другое количество раз.
Теорема.
Наивероятнейшее
число наступлений события
в
независимых испытаниях заключено между
числамии
.
Доказательство.
По формуле Бернулли при
:
Следовательно,
вероятность
будет больше, меньше или равна вероятности
в зависимости от того, какое из трех
соотношений будет выполняться:
|
|
|
|
Если
переписать эти соотношения в более
простом виде:
|
|
|
|
То
приходим к выводу, что:
,
если
;
,
если
;
,
если
.
Следовательно,
вероятность
при
возрастает, а при
– убывает. В случае, когда
не является целым числом, для
наивероятнейшего числа наступлений
события(обозначим его
)
должно выполняться неравенство,
что возможно при,
т.е. при.
В то же время, должно выполняться
неравенство,
что возможно при,
т.е. при.
Таким образом,.
Заметим,
что разность между
и
равна единице, значит, в большинстве
случаев числоединственно. Если
– целое число, то наивероятнейших чисел
два:
и
.
В этом случае, поскольку
,
то,
а
.
Полиномиальная
схема
Схему
независимых испытаний Бернулли еще
называют биномиальной
схемой,
поскольку она рассматривает
последовательности испытаний с двумя
исходами. От нее можно перейти к более
общей полиномиальной схеме последовательных
независимых испытаний, в каждом из
которых возможны
исходов с вероятностями
,
,
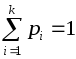
В этом случае пространство элементарных
исходов содержиттаких событий. Вероятность того, что из
испытаний
закончатся первым исходом,
– вторым исходом, …,
–
-ым
исходом равна:
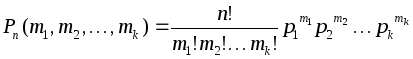
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача 1
Прямоугольник
со сторонами l1 и l2 разделен на четыре равные
части, одна из которых заштрихована. На прямоугольник брошены три точки.
Попадание точки в любое место прямоугольника равновозможно. Дискретная случайная величина – число точек,
попавших на заштрихованную часть. Найти: закон распределения, числовые
характеристики, функцию распределения F(x). Построить график F(x).
Задача 2
Для
случайной величины X найти: а) закон распределения; б) функцию
распределения; в) математическое ожидание и дисперсию. При установившемся
технологическом процессе всей
производимой продукции станок-автомат выпускает 2/3 первым сортом и 1/3 — вторым. Случайным образом отбирается 5
изделий. X — число изделий первого сорта среди отобранных.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 3
Игральную
кость подбросили 3 раза. Найти математическое ожидание, дисперсию, среднее
квадратическое отклонение числа невыпадения единицы.
Задача 4
Монету
подбросили 4 раза. Найти математическое ожидание, дисперсию, среднее
квадратическое отклонение дискретной случайной величины X –
числа появлений герба.
Задача 5
В городе
имеется N=3 оптовых баз. Вероятность того, что требуемого сорта товар
отсутствует, на этих базах одинакова и равна p=0,2. Составить закон
распределения числа баз, на которых товар отсутствует в данный момент. Найти
математическое ожидание и среднее квадратическое отклонение.
Задача 6
Продавец
азартных игр объясняет, что в его лотерее 40% заклепок. Игрок покупает 5
билетов.
а) Какова
вероятность того, что он вытащит не более двух заклепок?
б)
Рассчитайте ожидаемое значение и интерпретируйте его
Задача 7
Случайные
величины ξ и η имеют биномиальные распределения с параметрами n=20 и p=0,2
для величины ξ и n=100 и p=0,1 для величины η.
Найти
математическое ожидание и дисперсию величины γ=10ξ-2η, если известен
коэффициент корреляции ρ(ξ,η)=-0,7.
Задача 8
Вероятность
изготовления бракованной детали на первом станке составляет 3%, на второй
станке – 5%. На первом станке изготовлено 20 деталей, на втором 40 деталей.
Найти математическое ожидание и дисперсию числа бракованных деталей.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 9
Производится
9 бомбометаний с вероятностью попадания при каждом 0,89. Какова вероятность при
более чем 4 бомбометаниях? Найти характеристики распределения случайной
величины.
Задача 10
Вероятность
того, что саженец абрикоса приживется в Новосибирской области, равна 0,6.
Посадили 5 саженцев. Записать закон распределения случайной величины X –
число прижившихся саженцев. Найти математическое ожидание и дисперсию
полученного распределения.
Задача 11
Из
курьерской службы отправились на объекты 5 курьеров. Каждый курьер с
вероятностью 0,3 независимо от других опаздывает на объект. Указать вид
распределения случайной величины X – числа опоздавших
курьеров. Построить ряд распределения случайной величины X.
Найти ее математическое ожидание и дисперсию. Найти вероятность того, что на
объекты опоздают не менее двух курьеров.
Задача 12
Проведено
5 независимых опытов. Вероятность взрыва в каждом опыте равна p=2/7.
Составить закон распределения числа взрывов, вычислить математическое ожидание,
дисперсию, среднеквадратическое отклонение и построить многоугольник
распределения.
Задача 13
На складе
производителя электрических гирлянд, которые планируется поставлять на продажу,
проводится выборочная проверка их работоспособности. Известно, что у примерно
5% производимых гирлянд бывают неисправности различного рода. Предположим, были
отобраны 3 гирлянды для проверки их работоспособности. Найдите закон
распределения случайной величины
– число гирлянд без неисправностей среди
отобранных. Определите вероятность того, что более чем одна гирлянда будет
исправлена.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Торговый
агент в среднем контактирует с 4 потенциальными покупателями в день. Из опыта
ему известно, что вероятность того, что потенциальный покупатель совершит
покупку, равна 0,023. Составить закон распределения ежедневного числа продаж
для агента. Найти числовые характеристики этого распределения. Чему равна
вероятность того, что у агента будет хотя бы 2 продажи в течение дня?
Задача 15
Случайная
величина имеет биноминальное распределение с математическим ожиданием M(X)=3 и
дисперсией D(X)=1,2. Найти P(X≥2).
Задача 16
По мишени
производится 4 независимых выстрела с вероятностью попадания при каждом
выстреле p=0,9. Найти закон распределения дискретной
случайной величины X, равной числу попадания в мишень. Написать функцию
распределения.
Задача 17
Производится
4 независимых выстрела по некоторой цели. Вероятность попадания при одном
выстреле равна 0,25. Выписать ряд распределения для числа попаданий в цель.
Задача 18
Вероятность
попадания в цель одним выстрелом равна 0,5. Производят пять выстрелов. Найти:
а) Распределение вероятностей числа попаданий; б) Наивероятнейшее число
попаданий; в) Вероятность, что попаданий будет не более двух.
Задача 19
Клиенты
банка не возвращают полученный кредит в 12% случаев.
а)
составить ряд распределения числа не отдавших кредит клиентов из взятых наудачу
3-х.
б) найти
среднее число не отдавших кредит клиентов и отклонение от него.
Задача 20
При
установившемся технологическом процессе происходит в среднем 10 обрывов нити на
100 веретен в час. Найти закон распределения и математическое ожидание
случайного числа обрывов нити в течение часа среди трех веретен, работающих
независимо друг от друга.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 21
Составить
закон распределения случайной величины Х и найти ее математическое ожидание,
дисперсию и среднее квадратическое отклонение:
Х – число
выигравших билетов лотереи, если куплено 3 билета, а выигрышные билеты
составляют в тираже 8%;
Задача 22
Производится
3 независимых опыта, в каждом из которых событие A появляется с вероятностью
0,4. Построить ряд распределения числа появлений события в 3-х опытах.
Найти F(X),M(X),D(X),σ(X),p(x≥1)
Задача 23
Построить
ряд распределения числа попаданий мячом в корзину при 4 бросках, если
вероятность попадания равна 0,7.
Задача 24
Производится
три независимых испытания, в каждом из которых вероятность появления события A равна
0,4. Составить закон распределения дискретной случайной величины X —
числа появления события A в указанных испытаниях.
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
Задача 25
Запишите
таблицу для данного закона распределения случайной величины X,
постройте многоугольник распределения. Найдите числовые характеристики распределения
(M(X),D(X),σ(X)). Запишите функцию распределения и постройте ее график.
Ответьте на вопрос о вероятности описанного события.
Записи
страховой компании показали, что 30% держателей страховых полисов старше 50 лет
потребовали возмещения страховых сумм. Для проверки в случайном порядке было
отобрано 5 человек старше 50 лет, имеющих полисы. Случайная величина X –
количество требующих возмещения среди отобранных. Чему равна вероятность того,
что потребуют возмещения более трех человек?
Задача 26
На
некоторой остановке автобус останавливается только по требованию. Вероятность
остановки равна 0,2. За смену автобус проходит мимо этой остановки 5 раз.
Составить закон распределения числа остановки за смену, найти математическое
ожидание и дисперсию этой случайной величины.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 27
Устройство
состоит из пяти независимых элементов. Вероятность безотказной работы каждого
элемента в одном опыте равна 0,7. Для случайной величины X
элементов, безотказно работавших в одном опыте, построить закон распределения,
их графики, найти ее числовые характеристики.
Задача 28
В группе
студентов среднее число отличников составляет 20%. Составить закон распределения количества
отличников среди четырех студентов, отобранных случайным образом для участия в
деловой игре.
Задача 29
В урне 6
белых и 14 черных шара. Из урны извлекается один шар 4 раз подряд, причем
каждый раз вынутый шар возвращается в урну и шары перемешиваются. Приняв за
случайную величину Х число извлеченных белых шаров, составить закон
распределения этой случайной величины, найти ее математическое ожидание и
дисперсию.
Задача 30
Устройство состоит из трех
независимо работающих элементов. Вероятность отказа в одном опыте для каждого
элемента равна 0.1. Составить закон распределения случайного числа отказавших
элементов в одном опыте. Составить функцию распределения, построить ее график.
Задача 31
В
контрольной работе три задачи. Вероятность того, что задача будет решена, равна
0,9. Найти математическое ожидание случайной величины – числа решенных задач,
стандартное отклонение.
Задача 32
Известна
вероятность события A: p(A)=0,6. Дискретная случайная
величина ξ – число появлений A в трех опытах. Построить
ряд распределения случайной величины ξ. Найти математическое
ожидание mξ и дисперсию Dξ.
Традиционная интерпретация 20-го века
Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из 

Определение
Пусть 
Построим случайную величину 
.
Тогда 




где 
Функция распределения
Функция распределения биномиального распределения может быть записана в виде суммы:
,
где 

.
Моменты
Производящая функция моментов биномиального распределения имеет вид:
,
откуда
,
,
а дисперсия случайной величины.
.
Свойства биномиального распределения
Биномиальное распределение не может быть распределением одной случайной величины
Доказательство первое
Если биномиальное распределение одной случайной величины имеет математическое ожидание 


Что и требовалось доказать
Доказательство второе — Буняковского
Биномиальное распределение двух случайных величин было получено путем разложения бинома по степеням и делением каждого члена разложения на весь бином. [1]
В современной записи биномиальное распределение Буняковского имеют следующий вид:
Связь с другими распределениями
- Если
, то, очевидно, получаем распределение Бернулли.
- Если
большое, то в силу центральной предельной теоремы
, где
— нормальное распределение.
- Если
большое, а
— фиксированное число, то
, где
— распределение Пуассона с параметром
,
- Если число случайных величин распределения больше двух, то обязаны получить мультиномиальное распределение независимых случайных величин.
Литература
- ↑ Буняковский В. Я. ОСНОВАНИЯ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ВЕРОЯТНОСТЕЙ сочинение В. Я. БУНЯКОВСКОГО, ИМПЕРАТОРСКОЙ АКАДЕМИИ НАУК, ОРДИНАРНОГО АКАДЕМИКА, ПРОФЕССОРА С. ПЕТЕРБУРГСКОГО УНИВЕРСИТЕТА, ДОКТОРА МАТЕМАТИЧЕСКИХ НАУК ПАРИЖСКОЙ АКАДЕМИИ. САНКТПЕТЕРБУРГ. В Типографии Императорской Академии Наук. 1846. 477 с.
См. также
- Парадоксы биномиального распределения
- Биномиальное распределение Буняковского
- Биномиальное распределение двух случайных величин
- Биномиальное распределение с равновероятными успехами испытаний Бернулли
- Парадоксы мультиномиального распределения
- Мультиномиальное распределение независимых случайных величин
- Мультиномиальное распределение зависимых случайных величин
- Мультиномиальное распределение с равновероятными успехами испытаний Бернулли
|
править |
Это краткий критический анализ статьи из русскоязычной энциклопедии http://ru.math.wikia.com/wiki/Биномиальное_распределение — Математика.
.
Не все явления измеряются в количественной шкале типа 1, 2, 3 … 100500 … Не всегда явление может принимать бесконечное или большое количество различных состояний. Например, пол у человека может быть либо М, либо Ж. Стрелок либо попадает в цель, либо не попадает. Голосовать можно либо «За», либо «Против» и т.д. и т.п. Другими словами, такие данные отражают состояние альтернативного признака – либо «да» (событие наступило), либо «нет» (событие не наступило). Наступившее событие (положительный исход) еще называют «успехом».
Эксперименты с такими данными называются схемой Бернулли, в честь известного швейцарского математика, который установил, что при большом количестве испытаний соотношение положительных исходов и общего количества испытаний стремится к вероятности наступления этого события.
Переменная альтернативного признака
Для того, чтобы в анализе задействовать математический аппарат, результаты подобных наблюдений следует записать в числовом виде. Для этого положительному исходу присваивают число 1, отрицательному – 0. Другими словами, мы имеем дело с переменной, которая может принимать только два значения: 0 или 1.
Какую пользу отсюда можно извлечь? Вообще-то не меньшую, чем от обычных данных. Так, легко подсчитать количество положительных исходов – достаточно просуммировать все значения, т.е. все 1 (успехи). Можно пойти далее, но для этого потребуется ввести парочку обозначений.
Первым делом нужно отметить, что положительные исходы (которые равны 1) имеют некоторую вероятность появления. Например, выпадение орла при подбрасывании монеты равно ½ или 0,5. Такая вероятность традиционно обозначается латинской буквой p. Следовательно, вероятность наступления альтернативного события равна 1 — p, которую еще обозначают через q, то есть q = 1 – p. Указанные обозначения можно наглядно систематизировать в виде таблички распределения переменной X.
Мы получили перечень возможных значений и их вероятности. Можно рассчитать математическое ожидание и дисперсию. Матожидание – это сумма произведений всех возможных значений на соответствующие им вероятности:
Вычислим матожидание, используя обозначения в таблицы выше.
Получается, что математическое ожидание альтернативного признака равно вероятности этого события – p.
Теперь определим, что такое дисперсия альтернативного признака. Дисперсия – есть средний квадрат отклонений от математического ожидания. Общая формула (для дискретных данных) имеет вид:
Отсюда дисперсия альтернативного признака:
Нетрудно заметить, что эта дисперсия имеет максимум 0,25 (при p=0,5).
Стандартное отклонение – корень из дисперсии:
Максимальное значение не превышает 0,5.
Как видно, и математическое ожидание, и дисперсия альтернативного признака имеют очень компактный вид.
Биномиальное распределение случайной величины
Рассмотрим ситуацию под другим углом. Действительно, кому интересно, что среднее выпадение орлов при одном бросании равно 0,5? Это даже невозможно представить. Интересней поставить вопрос о числе выпадения орлов при заданном количестве бросков.
Другими словами, исследователя часто интересует вероятность наступления некоторого числа успешных событий. Это может быть количество бракованных изделий в проверяемой партии (1- бракованная, 0 — годная) или количество выздоровлений (1 – здоров, 0 – больной) и т.д. Количество таких «успехов» будет равно сумме всех значений переменной X, т.е. количеству единичных исходов.
Случайная величина B называется биномиальной и принимает значения от 0 до n (при B = 0 – все детали годные, при B = n – все детали бракованные). Предполагается, что все значения x независимы между собой. Рассмотрим основные характеристики биномиальной переменной, то есть установим ее математическое ожидание, дисперсию и распределение.
Матожидание биномиальной переменной получить очень легко. Математическое ожидание суммы величин есть сумма математических ожиданий каждой складываемой величины, а оно у всех одинаковое, поэтому:
Например, математическое ожидание количества выпавших орлов при 100 подбрасываниях равно 100 × 0,5 = 50.
Теперь выведем формулу дисперсии биномиальной переменной. Дисперсия суммы независимых случайных величин есть сумма дисперсий. Отсюда
Стандартное отклонение, соответственно
Для 100 подбрасываний монеты стандартное отклонение количества орлов равно
И, наконец, рассмотрим распределение биномиальной величины, т.е. вероятности того, что случайная величина B будет принимать различные значения k, где 0≤ k ≤n. Для монеты эта задача может звучать так: какова вероятность выпадения 40 орлов при 100 бросках?
Чтобы понять метод расчета, представим, что монета подбрасывается всего 4 раза. Каждый раз может выпасть любая из сторон. Мы задаемся вопросом: какова вероятность выпадения 2 орлов из 4 бросков. Каждый бросок независим друг от друга. Значит, вероятность выпадения какой-либо комбинации будет равна произведению вероятностей заданного исхода для каждого отдельного броска. Пусть О – это орел, Р – решка. Тогда, к примеру, одна из устраивающих нас комбинаций может выглядеть как ООРР, то есть:
Вероятность такой комбинации равняется произведению двух вероятностей выпадения орла и еще двух вероятностей не выпадения орла (обратное событие, рассчитываемое как 1 — p), т.е. 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. Такова вероятность одной из устраивающих нас комбинации. Но вопрос ведь стоял об общем количестве орлов, а не о каком-то определенном порядке. Тогда нужно сложить вероятности всех комбинаций, в которых присутствует ровно 2 орла. Ясно, все они одинаковы (от перемены мест множителей произведение не меняется). Поэтому нужно вычислить их количество, а затем умножить на вероятность любой такой комбинации. Подсчитаем все варианты сочетаний из 4 бросков по 2 орла: РРОО, РОРО, РООР, ОРРО, ОРОР, ООРР. Всего 6 вариантов.
Следовательно, искомая вероятность выпадения 2 орлов после 4 бросков равна 6×0,0625=0,375.
Однако подсчет подобным образом утомителен. Уже для 10 монет методом перебора получить общее количество вариантов будет очень трудно. Поэтому умные люди давно изобрели формулу, с помощью которой рассчитывают количество различных сочетаний из n элементов по k, где n – общее количество элементов, k – количество элементов, варианты расположения которых и подсчитываются. Формула сочетания из n элементов по k такова:
Подобные вещи проходят в разделе комбинаторики. Всех желающих подтянуть знания отправляю туда. Отсюда, кстати, и название биномиального распределения (формула выше является коэффициентом в разложении бинома Ньютона).
Формулу для определения вероятности легко обобщить на любое количество n и k. В итоге формула биномиального распределения имеет следующий вид.
Количество подходящих под условие комбинаций умножить на вероятность одной из них.
Для практического использования достаточно просто знать формулу биномиального распределения. А можно даже и не знать – ниже показано, как определить вероятность с помощью Excel. Но лучше все-таки знать.
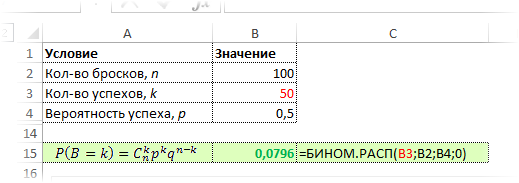
Рассчитаем по этой формуле вероятность выпадения 40 орлов при 100 бросках:
Или всего 1,08%. Для сравнения вероятность наступления математического ожидания этого эксперимента, то есть 50 орлов, равна 7,96%. Максимальная вероятность биномиальной величины принадлежит значению, соответствующему математическому ожиданию.
Расчет вероятностей биномиального распределения в Excel
Если использовать только бумагу и калькулятор, то расчеты по формуле биномиального распределения, несмотря на отсутствие интегралов, даются довольно тяжело. К примеру значение 100! – имеет более 150 знаков. Раньше, да и сейчас тоже, для вычисления подобных величин использовали приближенные формулы. В настоящий момент целесообразно использовать специальное ПО, типа MS Excel. Таким образом, любой пользователь (даже гуманитарий по образованию) вполне может вычислить вероятность значения биномиально распределенной случайной величины.
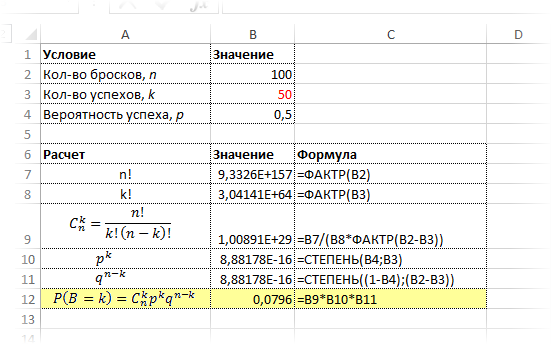
Для закрепления материала задействуем Excel пока в качестве обычного калькулятора, т.е. произведем поэтапное вычисление по формуле биномиального распределения. Рассчитаем, например, вероятность выпадения 50 орлов. Ниже приведена картинка с этапами вычислений и конечным результатом.
Как видно, промежуточные результаты имеют такой масштаб, что не помещаются в ячейку, хотя везде и используются простые функции типа: ФАКТР (вычисление факториала), СТЕПЕНЬ (возведение числа в степень), а также операторы умножения и деления. Более того, этот расчет довольно громоздок, во всяком случаен не является компактным, т.к. задействовано много ячеек. Да и разобраться с ходу трудновато.
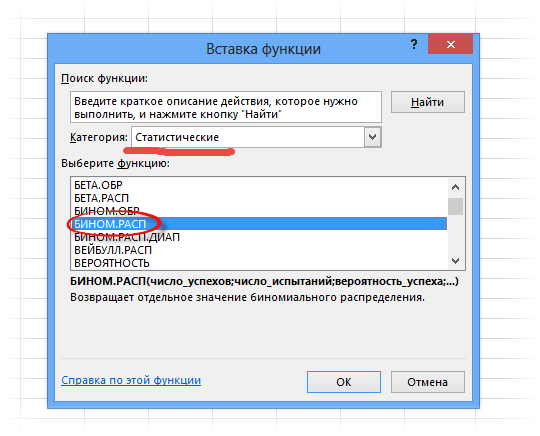
В общем в Excel предусмотрена готовая функция для вычисления вероятностей биномиального распределения. Функция называется БИНОМ.РАСП.
Синтаксис функции состоит из 4 аргументов:
Поля имеют следующие назначения:
Число успехов – количество успешных испытаний. У нас их 50.
Число испытаний – количество бросков: 100 раз.
Вероятность успеха – вероятность выпадения орла при одном подбрасывании 0,5.
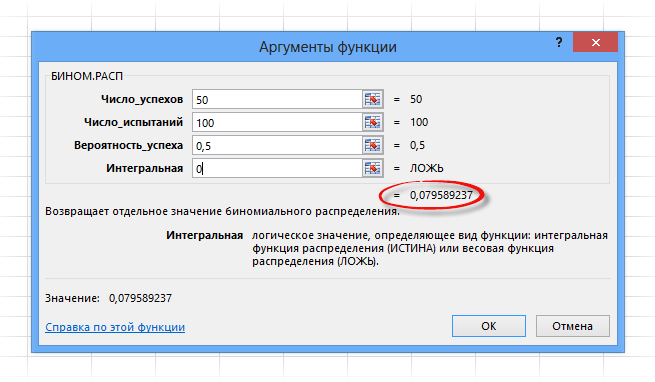
Интегральная – указывается либо 1, либо 0. Если 0, то рассчитается вероятность P(B=k); если 1, то рассчитается функция биномиального распределения, т.е. сумма всех вероятностей от B=0 до B=k включительно.
Нажимаем ОК и получаем тот же результат, что и выше, только все рассчиталось одной функцией.
Очень удобно. Эксперимента ради вместо последнего параметра 0 поставим 1. Получим 0,5398. Это значит, что при 100 подкидываниях монеты вероятность выпадения орлов в количестве от 0 до 50 равна почти 54%. А поначалу то казалось, что должно быть 50%. В общем, расчеты производятся легко и быстро.
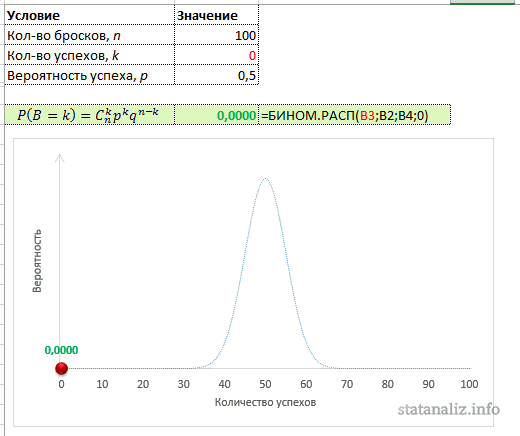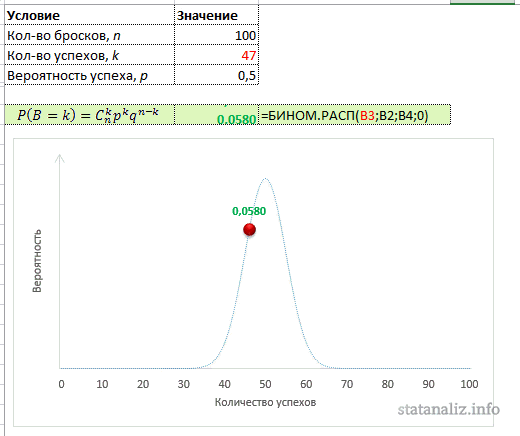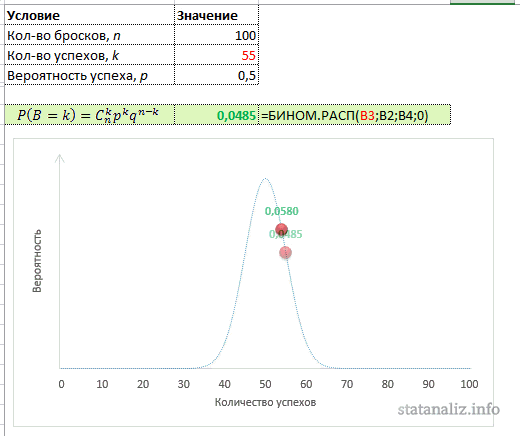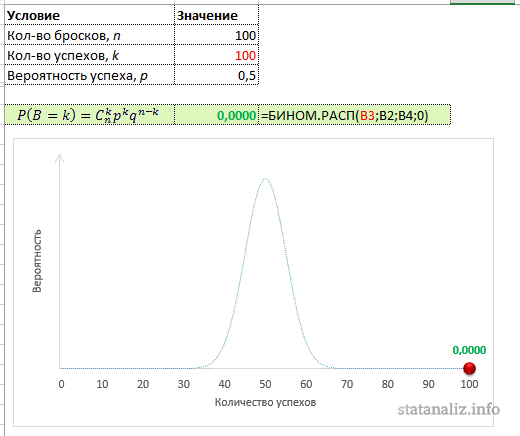
Настоящий аналитик должен понимать, как ведет себя функция (каково ее распределение), поэтому произведем расчет вероятностей для всех значений от 0 до 100. То есть зададимся вопросом: какова вероятность, что не выпадет ни одного орла, что выпадет 1 орел, 2, 3, 50, 90 или 100. Расчет приведен в следующей картинке. Синяя линия – само биномиальное распределение, красная точка – вероятность для конкретного числа успехов k.
Кто-то может спросить, а не похоже ли биномиальное распределение на… Да, очень похоже. Еще Муавр (в 1733 г.) говорил, что биномиальное распределение при больших выборках приближается к нормальному закону (не знаю, как это тогда называлось), но его никто не слушал. Только Гаусс, а затем и Лаплас через 60-70 лет вновь открыли и тщательно изучили нормальной закон распределения. На графике выше отлично видно, что максимальная вероятность приходится на математическое ожидание, а по мере отклонения от него, резко снижается. Также, как и у нормального закона.
Биномиальное распределение имеет большое практическое значение, встречается довольно часто. С помощью Excel расчеты проводятся легко и быстро.
Поделиться в социальных сетях:
Биномиальное распределение — одно из важнейших распределений вероятностей дискретно изменяющейся случайной величины.
Биномиальным распределением называется распределение вероятностей числа m наступления события А в n взаимно независимых наблюдениях.
Часто событие А называют «успехом» наблюдения, а противоположное ему событие — «неуспехом», но это обозначение весьма условное.
Условия биномиального распределения:
- в общей сложности проведено n испытаний, в которых событие А может наступить или не наступить;
- событие А в каждом из испытаний может наступить с одной и той же вероятностью p;
- испытания являются взаимно независимыми.
Вероятность того, что в n испытаниях событие А наступит именно m раз, можно вычислить по формуле Бернулли:
или
где p — вероятность наступления события А;
q = 1 — p — вероятность наступления противоположного события .
Разберёмся, почему биномиальное распределение описанным выше образом связано с формулой Бернулли. Событие — число успехов при n испытаниях распадается на ряд вариантов, в каждом из которых успех достигается в m испытаниях, а неуспех — в n — m испытаниях. Рассмотрим один из таких вариантов — B1. По правилу сложения вероятностей умножаем вероятности противоположных событий:
а если обозначим q = 1 — p, то
Такую же вероятность будет иметь любой другой вариант, в котором m успехов и n — m неуспехов. Число таких вариантов равно — числу способов, которыми можно из n испытаний получить m успехов.
Сумма вероятностей всех m чисел наступления события А (чисел от 0 до n) равна единице:

где каждое слагаемое представляет собой слагаемое бинома Ньютона. Поэтому рассматриваемое распределение и называется биномиальным распределением.
На практике часто необходимо вычислять вероятности «не более m успехов в n испытаниях» или «не менее m успехов в n испытаниях». Для этого используются следующие формулы.
Интегральную функцию, то есть вероятность F(m) того, что в n наблюдениях событие А наступит не более m раз, можно вычислить по формуле:
В свою очередь вероятность F(≥m) того, что в n наблюдениях событие А наступит не менее m раз, вычисляется по формуле:
Иногда бывает удобнее вычислять вероятность того, что в n наблюдениях событие А наступит не более m раз, через вероятность противоположного события:
- Какой из формул пользоваться, зависит от того, в какой из них сумма содержит меньше слагаемых.
- Характеристики биномиального распределения вычисляются по следующим формулам.
- Математическое ожидание: .
- Дисперсия: .
- Среднеквадратичное отклонение: .
Биномиальное распределение и расчёты в MS Excel
Вероятность биномиального распределения Pn(m) и значения интегральной функции F(m) можно вычислить при помощи функции MS Excel БИНОМ.РАСП. Окно для соответствующего расчёта показано ниже (для увеличения нажать левой кнопкой мыши).

MS Excel требует ввести следующие данные:
- число успехов;
- число испытаний;
- вероятность успеха;
- интегральная — логическое значение: 0 — если нужно вычислить вероятность Pn(m) и 1 — если вероятность F(m).
Пример 1. Менеджер фирмы обобщил информацию о числе проданных в течение последних 100 дней фотокамер. В таблице обобщена информация и рассчитаны вероятности того, что в день будет продано определённое число фотокамер.
| Продано в день | Число дней | Вероятность |
| 10 | 8 | 0,08 |
| 11 | 12 | 0,12 |
| 12 | 19 | 0,19 |
| 13 | 23 | 0,23 |
| 14 | 18 | 0,18 |
| 15 | 20 | 0,20 |
| Всего | 100 | 1,00 |
День завершён с прибылью, если продано 13 или более фотокамер. Вероятность, что день будет отработан с прибылью:
Вероятность того, что день будет отработан без прибыли:
Пусть вероятность того, что день отработан с прибылью, является постоянной и равна 0,61, и число проданных в день фотокамер не зависит от дня. Тогда можно использовать биномиальное распределение, где событие А — день будет отработан с прибылью, — без прибыли.
- Вероятность того, что из 6 дней все будут отработаны с прибылью:
- .
- Тот же результат получим, используя функцию MS Excel БИНОМ.РАСП (значение интегральной величины — 0):
P6(6) = БИНОМ.РАСП(6; 6; 0,61; 0) = 0,052.
- Вероятность того, что из 6 дней 4 и больше дней будут отработаны с прибылью:
- ,
- где ,
- ,
- ,
- .
- Используя функцию MS Excel БИНОМ.РАСП, вычислим вероятность того, что из 6 дней не более 3 дней будут завершены с прибылью (значение интегральной величины — 1):
P6(≤3) = БИНОМ.РАСП(3; 6; 0,61; 1) = 0,435.
- Вероятность того, что из 6 дней все будут отработаны с убытками:
- ,
- Тот же показатель вычислим, используя функцию MS Excel БИНОМ.РАСП:
P6(0) = БИНОМ.РАСП(0; 6; 0,61; 0) = 0,0035.
Решить задачу самостоятельно, а затем посмотреть решение
Пример 2. В урне 2 белых шара и 3 чёрных. Из урны вынимают шар, устанавливают цвет и кладут обратно. Попытку повторяют 5 раз. Число появления белых шаров — дискретная случайная величина X, распределённая по биномиальному закону. Составить закон распределения случайной величины. Определить моду, математическое ожидание и дисперсию.
Правильное решение и ответ.
Нет времени вникать в решение? Можно заказать работу!
Продолжаем решать задачи вместе
Пример 3. Из курьерской службы отправились на объекты n = 5 курьеров. Каждый курьер с вероятностью p = 0,3 независимо от других опаздывает на объект.
Дискретная случайная величина X — число опоздавших курьеров. Построить ряд распределения это случайной величины. Найти её математическое ожидание, дисперсию, среднее квадратическое отклонение.
Найти вероятность того, что на объекты опоздают не менее двух курьеров.
Решение. Случайная величина X — число опоздавших курьеров — распределена по биномиальному закону. Под наблюдением понимается отправка курьера на объект, а под «успехом» удобнее понимать его опоздание. Найдём вероятности возможных значений случайной величины и округлим их до трёх знаков после запятой:
Ряд распределения будет иметь вид:
| 1 | 2 | 3 | 4 | 5 | |
| 0,168 | 0,360 | 0,309 | 0,133 | 0,028 | 0,002 |
- Математическое ожидание случайной величины: .
- Дисперсия случайной величины: .
- Среднеквадратичное отклонение: .
- Найдём вероятность того, что на объекты опоздают не менее двух курьеров:
Пример 4. Игральная кость бросается четыре раза. Найти вероятность того, что шестёрка появится а) ровно один раз; б) хотя бы один раз.
Решение. Случайная величина X — число появлений шестёрки — имеет биномиальное распределение с параметрами n = 4; p = 1/6.
а) .
б)
Пройти тест по теме Теория вероятностей и математическая статистика
Начало темы «Теория вероятностей»
Действия над вероятностями Различные задачи на сложение и умножение вероятностей Формула полной вероятности Независимые испытания и формула Бернулли Распределение вероятностей дискретной случайной величины Распределение вероятностей непрерывной случайной величины Математическое ожидание и дисперсия случайной величины Распределение Пуассона дискретной случайной величины Равномерное распределение непрерывной случайной величины Нормальное распределение непрерывной случайной величины
Источник: https://function-x.ru/probabilities_distribution_binomial.html
Биномиальное распределение. Задачи
Целочисленная случайная величина X имеет биномиальное распределение, если вероятность ее возможных значений вычисляется по формуле Бернулли
В табличной форме этот закон имеет следующий вид:
При проверке выполнения условия нормировки используется формула бинома Ньютона, поэтому закон распределения называют биномиальным
Построим вероятностную образующую функцию для этого закона
Итак, вероятностная образующая функция для биномиального закона ровна
- Найдем основные числовые характеристики для этого закона
- 1. Математическое ожидание случайной величины через образующую функцию для биномиального распределения вычисляем по формуле
- 2. Вторая производная от образующей функции для биномиального распределения в единице примет значение
- На основе найденного значения можно вычислять дисперсию
- Имея дисперсию нетрудно установить среднее математическое отклонение
- 3. Коэффициент асимметрии А(Х) и эксцесс Е(Х) для биномиального распределения определяют по формулам
- В случае роста количества испытаний n асимметрия и эксцесс стремятся к нулю.
- Перейдем к практической стороне биномиального распределения
Задача 1. В партии однотипных деталей стандартные составляют 97%. Наугад из партии берут 400 деталей. Определить математическое ожидание, дисперсию и среднее квадратическое отклонение М(Х), D(X), S(Х) для дискретной случайной величины Х — появления числа стандартных деталей среди 400 наугад взятых.
Решение. Целочисленных случайная величина Х имеет биномиальное закон распределения вероятностей, которая может принимать значения Х = k = 0, 1, 2, …, 400.
Вероятности возможных значений для данной задачи определяются по формуле Бернулли и составляют где р = 0,97 — вероятность появления стандартной детали, q = 1 – p =1 – 0,97 = 0,03 — вероятность появления нестандартной детали.
Согласно приведенным выше формулам определяем нужные величины:
- ————————————
Задача 2. Два ювелирные заводы производят свадебные кольца в объеме 3:7. Первый завод производит 95% колец без дефекта, второй – 90%. Молодая пара перед свадьбой покупает пару колец. Построить закон распределения, вычислить математическое ожидание и среднее квадратичное отклонение.
- Решение. Вероятность события А – куплена кольцо оказалась качественной определим по формуле полной вероятности
- Случайная величина Х – количество колец надлежащего качества среди купленных имеет биномиальное закон распределения с параметрами
- Найдем соответствующие вероятности
- Запишем таблицу распределения
- На основе табличных данных вычисляем математическое ожидание
- дисперсию
- Среднее квадратичное отклонение
Как можно убедиться из примеров, биномиальний закон распределения простой как для понимания так и для вычислений. Хорошо разберитесь с примерами и пользуйтесь биномиальным распределением там где это необходимо.
Источник: https://yukhym.com/ru/zakony-raspredeleniya/binomialnoe-raspredelenie-zadachi.html
Биномиальное распределение примеры
- Биномиальный закон распределения случайной величины определяется при помощи формулы Бернулли:
Рассмотрим примеры применения формулы Бернулли для построения биномиальных законов распределения дискретной случайной величины X. - Пример 1
- Написать биномиальный закон распределения дискретной случайной величины X –числа появлений «герба» при двух бросаниях монеты.
- Решение
При бросании монеты вероятность выпадения «герба» равна 0.5, а «решки» q=1–p=1-0.5=0.5
- Также случайная величина X — числа появлении «герба» принимает значения: 0, 1, 2
- Найдём значения случайной величины X:
и в виде таблицы составим биномиальный закон распределения СВ X:- Пример 2
Две игральные кости одновременно бросают два раза. Написать биномиальный закон распределения дискретной случайной величины X — числа выпадений четного числа очков на двух игральных костях.
Решение
По условию задачи, кость бросается два раза — составим в виде таблицы всевозможные комбинации выпадения четного и нечетного числа очков
| Первая кость | Вторая кость |
| Четное число очков | Четное число очков |
| Четное число очков | Нечетное число очков |
| Нечетное число очков | Четное число очков |
| Нечетное число очков | Нечетное число очков |
В соответствии с таблицей, из четырёх комбинаций числа выпадений четного числа равна единице, следовательно, р=1/4=0.25, а не выпадения — q=1–p=1-0.25=0.
75
Дискретная случайная величина X принимает следующие значения: 0, 1, 2
По формуле Бернулли составим биномиальный закон распределения СВ X:

| X | 1 | 2 | |
| P | 0.5625 | 0.375 | 0.0625 |
Пример 3
В партии 10% нестандартных деталей. Наудачу отобраны четыре детали. Написать биномиальный закон распределения дискретной случайной величины X — числа нестандартных деталей среди четырех отобранных.
Решение
Из условия задачи p = 0.1, q=1–р=0.
9
Возможные варианты значений СВ X: 0, 1, 2, 3, 4
По формуле Бернулли имеем:

| X | 1 | 2 | 3 | 4 | |
| P | 0.6561 | 0.2916 | 0.0486 | 0.0036 | 0.0001 |
Пример 4
Студенты техникума вышли на посадку цветов. Всхожесть семян цветов оценивается вероятностью 0,6. Какова вероятность, что из 10 посеянных цветов взойдет 5?
Решение
${P_{10}}left( 5
ight) = Pleft( {X = 5}
ight) = C_{10}^5{0,6^5}{0,4^{10 — 5}} ≈0,2$
Пример 5
В библиотеке 50000 книг. Из них 1000 на иностранных языках. Студент взял в библиотеке 20 книг. Какова вероятность, что среди них 5 на иностранных языках?
Решение
p=1000/50000=0,02
q=1−0,02=0,98
$P=frac{20!}{5!15!}·{0,02^5}·{0,98^{15}} ≈3,66·10^{-5}$
Источник: https://www.matematicus.ru/teoriya-veroyatnosti/binomialnoe-raspredelenie-primery
Биномиальное распределение. Дискретные распределения в EXCEL
Рассмотрим Биномиальное распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL БИНОМ.РАСП() построим графики функции распределения и плотности вероятности. Произведем оценку параметра распределения p, математического ожидания распределения и стандартного отклонения. Также рассмотрим распределение Бернулли.
Определение . Пусть проводятся n испытаний, в каждом из которых может произойти только 2 события: событие «успех» с вероятностью p или событие «неудача» с вероятностью q =1-p (так называемая Схема Бернулли, Bernoulli trials ).
Вероятность получения ровно x успехов в этих n испытаниях равна:
Примечание : Порядок получения успехов значения не имеет. Если важен порядок, то см. статью Отрицательное Биномиальное распределение .
Количество успехов в выборке x является случайной величиной, которая имеет Биномиальное распределение (англ. Binomial distribution ) p и n – являются параметрами этого распределения.
Примечание : Запись означает количество сочетаний из n элементов по x . Для сочетаний также используется запись . Подробнее о сочетаниях см. статью Сочетания без повторений: Комбинаторика в MS EXCEL .
Напомним, что для применения схемы Бернулли и соответственно Биномиального распределения, должны быть выполнены следующие условия:
- каждое испытание должно иметь ровно два исхода, условно называемых «успехом» и «неудачей».
- результат каждого испытания не должен зависеть от результатов предыдущих испытаний (независимость испытаний).
- вероятность успеха p должна быть постоянной для всех испытаний.
Биномиальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Биномиального распределения имеется функция БИНОМ.РАСП() , английское название — BINOM.
DIST(), которая позволяет вычислить вероятность того, что в выборке будет ровно х «успехов» (т.е. функцию плотности вероятности p(x), см.
формулу выше), и интегральную функцию распределения (вероятность того, что в выборке будет x или меньше «успехов», включая 0).
СОВЕТ : Подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .
До MS EXCEL 2010 в EXCEL была функция БИНОМРАСП() , которая также позволяет вычислить функцию распределения и плотность вероятности p(x). БИНОМРАСП() оставлена в MS EXCEL 2010 для совместимости.
- В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
- Биномиальное распределения имеет обозначение B ( n ; p ) .
Примечание : Для построения интегральной функции распределения идеально подходит диаграмма типа График , для плотности распределения – Гистограмма с группировкой . Подробнее о построении диаграмм читайте статью Основные типы диаграмм.
- Примечание : Для удобства написания формул в файле примера созданы Имена для параметров Биномиального распределения : n и p.
- В файле примера приведены различные расчеты вероятности с помощью функций MS EXCEL:
- Как видно на картинке выше, предполагается, что:
- В бесконечной совокупности, из которой делается выборка, содержится 10% (или 0,1) годных элементов (параметр p , третий аргумент функции = БИНОМ.РАСП() )
- Чтобы вычислить вероятность, того что в выборке из 10 элементов (параметр n , второй аргумент функции) будет ровно 5 годных элементов (первый аргумент), нужно записать формулу: =БИНОМ.РАСП(5; 10; 0,1; ЛОЖЬ)
- Последний, четвертый элемент, установлен =ЛОЖЬ, т.е. возвращается значение функции плотности распределения .
Если значение четвертого аргумента =ИСТИНА, то функция БИНОМ.РАСП() возвращает значение интегральной функции распределения или просто Функцию распределения . В этом случае можно рассчитать вероятность того, что в выборке количество годных элементов будет из определенного диапазона, например, 2 или меньше (включая 0).
Для этого нужно записать формулу: = БИНОМ.РАСП(2; 10; 0,1; ИСТИНА)
Примечание : При нецелом значении х, дробная часть отбрасывается . Например, следующие формулы вернут одно и тоже значение: =БИНОМ.РАСП( 2 ; 10; 0,1; ИСТИНА) =БИНОМ.РАСП( 2,9 ; 10; 0,1; ИСТИНА)
Примечание : В файле примера плотность вероятности и функция распределения также вычислены с использованием определения и функции ЧИСЛКОМБ() .
Показатели распределения
- В файле примера на листе Пример имеются формулы для расчета некоторых показателей распределения:
- Выведем формулу математического ожидания Биномиального распределения , используя Схему Бернулли .
- По определению случайная величина Х в схеме Бернулли (Bernoulli random variable) имеет функцию распределения :
- Это распределение называется распределение Бернулли .
- Примечание : распределение Бернулли – частный случай Биномиального распределения с параметром n=1.
- Найдем математическое ожидание ( среднее, mean ) распределения Бернулли ( x принимает только 2 значения).
Предположим, что мы провели n последовательных испытаний Бернулли и у нас сформировалась выборка , состоящая из n элементов: x1, x2, …, xn (каждое из которых равно 0 или 1). Сумма этих случайных величин Y=X1+X2+…+Xn, в свою очередь, также является случайной величиной и, как мы помним, будет иметь Биномиальное распределение с параметрами n и p .
- Учитывая, что математическое ожидание для каждого x i равно p , то для соответствующего Биномиального распределения μ=p*n.
- Аналогичным образом, можно вычислить дисперсию Биномиального распределения.
- Для этого сначала найдем дисперсию ( второй момент, variance ) распределения Бернулли :
Соответственно, дисперсия для Биномиального распределения равна σ 2 =n*p*(1-p)= n*p*q.
Генерация случайных чисел. Распределение Бернулли
- С помощью надстройки Пакет анализа можно сгенерировать случайные числа , извлеченные из распределения Бернулли .
- СОВЕТ : О надстройке Пакет анализа можно прочитать в статье Надстройка Пакет анализа MS EXCEL .
- Сгенерируем 3 массива по 100 чисел с различными вероятностями успеха: 0,1; 0,5 и 0,9.
Для этого в окне Генерация случайных чисел установим следующие параметры для каждой вероятности p:
Примечание : Если установить опцию Случайное рассеивание ( Random Seed ), то можно выбрать определенный случайный набор сгенерированных чисел. Например, установив эту опцию =25 можно сгенерировать на разных компьютерах одни и те же наборы случайных чисел (если, конечно, другие параметры распределения совпадают). Значение опции может принимать целые значения от 1 до 32 767. Название опции Случайное рассеивание может запутать. Лучше было бы ее перевести как Номер набора со случайными числами .
В итоге будем иметь 3 столбца по 100 чисел, на основании которых можно, например, оценить вероятность успеха p по формуле: Число успехов/100 (см. файл примера лист ГенерацияБернулли ).
Примечание : Для распределения Бернулли с p=0,5 можно использовать формулу =СЛУЧМЕЖДУ(0;1) , которая соответствует дискретному равномерному распределению .
Генерация случайных чисел. Биномиальное распределение
С помощью надстройки Пакет анализа можно сгенерировать случайные числа , извлеченные из Биномиального распределения .
Сгенерируем 3 массива по 100 чисел с различными вероятностями успеха: 0,1; 0,5; 0,9. Количество испытаний n установим 20. Для этого в окне Генерация случайных чисел установим следующие параметры для каждой вероятности p:
В итоге будем иметь 3 столбца чисел, на основании которых можно, например, оценить вероятность успеха p по формуле: Среднее значение успехов/ n (см. файл примера лист ГенерацияБином ).
Примечание : Для генерирования массива чисел, распределенных по Биномиальному закону , можно использовать формулу =БИНОМ.ОБР(20; p; СЛЧИС()) , где p – вероятность успеха. Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист ГенерацияБином ).
Оценка параметра p
В схеме Бернулли оценить параметр распределения p можно по формуле =СУММ(B14:B113)/СЧЁТ(B14:B113) . В формуле предполагается, что массив случайных чисел находится в диапазоне B14:B113 .
Оценить параметр Биномиального распределения p можно по формуле = СРЗНАЧ(B13:B112)/n (предполагается, что случайные числа сгенерированы формулой =БИНОМ.ОБР(n; p; СЛЧИС() ). Также в формуле предполагается, что массив случайных чисел находится в диапазоне B13:B112 .
Обратная функция БИНОМ.ОБР()
Вспомним график функции Биномиального распределения :
Решим задачу. Предположим, что для целей контроля качества нам требуется определить наибольшее допустимое количество дефектных изделий, которое еще позволяет обойтись без отбраковки всей партии.
Задана величина выборки из партии ( n =20) и р= 0,2 — доля дефектных изделий, которая обычно наблюдается в данном производственном процессе. Также пусть задана вероятность допустить ошибку 1-го рода (см.
статью про уровень доверия ) равная 90%. Пороговый приемочный критерий можно вычислить по формуле =БИНОМ.ОБР(20; 0,2; 90%) .
Формула вернет значение 6 — наибольшее количество дефектных изделий, допустимое в выборке .
Примечание : Третий аргумент функции БИНОМ.ОБР() называется Альфа ( α error, type I error, риск производителя, альфа-риск ) и представляет собой вероятность допустить ошибку 1-го рода при проверке статистической гипотезы (см. статью Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна) ).
Предположим, что в выборке обнаружилось 7 дефектных изделий. Это означает, что «очень вероятна» ситуация, что изменилась доля дефектных изделий p , которая является характеристикой нашего производственного процесса.
Хотя такая ситуация «очень вероятна», но существует вероятность (альфа-риск, ошибка 1-го рода, «ложная тревога»), что все же p осталась без изменений, а увеличенное количество дефектных изделий обусловлено случайностью выборки.
Как видно на рисунке ниже, 7 – количество дефектных изделий, которое допустимо для процесса с p=0,21 при том же значении Альфа .
Это служит иллюстрацией, что при превышении порогового значения дефектных изделий в выборке, p «скорее всего» увеличилось.
Фраза «скорее всего» означает, что существует всего лишь 10% вероятность (100%-90%) того, что отклонение доли дефектных изделий выше порогового вызвано только сучайными причинами.
Таким образом, превышение порогового количества дефектных изделий в выборке, может служить сигналом, что процесс расстроился и стал выпускать б о льший процент бракованных изделий.
Примечание : До MS EXCEL 2010 в EXCEL была функция КРИТБИНОМ() , которая эквивалентна БИНОМ.ОБР() . КРИТБИНОМ() оставлена в MS EXCEL 2010 и выше для совместимости.
Связь Биномиального распределения с другими распределениями
Если параметр n Биномиального распределения стремится к бесконечности, а p стремится к 0, то в этом случае Биномиальное распределение может быть аппроксимировано Распределением Пуассона . Можно сформулировать условия, когда приближение распределением Пуассона работает хорошо:
- p (чем меньше p и больше n , тем приближение точнее);
- p >0,9 (учитывая, что q =1- p , вычисления в этом случае необходимо производить через q (а х нужно заменить на n — x ). Следовательно, чем меньше q и больше n , тем приближение точнее).
При 0,1
Источник: https://excel2.ru/articles/binomialnoe-raspredelenie-diskretnye-raspredeleniya-v-ms-excel
Биномиальное распределение
Биномиальное распределение симметрично только в его ограничивающей форме. Это распределение именуется так из-за его отношения к разложению двучлена (p + q)n. Биномиальное выражение – это выражение, которое содержит два члена, соединенных знаком «плюс» или «минус».
Биномиальное распределение есть распределение вероятности исходов события, которые могут быть классифицированы как положительные или отрицательные, т.е. оно связано с обстоятельствами, в которых какое-либо специфическое событие может или случиться, или не случиться. Здесь нет места для полумер, и не принимается в расчет степень интенсивности события.
Общая вероятность события, случающегося или не случающегося, равна 1. Поэтому если вероятность того, что оно случится, равна p, то вероятность того, что оно не случится, равна q = 1 – p, p + q = 1.
Члены p и q относятся к вероятности наступления или ненаступления только одного события.
Вероятность наступления двух отдельных событий по закону умножения равна для независимых явлений: p × p = p2, т.е. 0,01 при p = 0,1. Вероятность ненаступления каждого из двух событий составляет q2 или 0,81.
Но возникает новая серия возможностей, поскольку в первом случае возможность того, что событие случится, связана с тем, что оно не случится во втором случае; вероятность этого равна p × q или 0,09. Аналогичным образом вероятность наступления события во втором случае, связанная с ненаступлением в первом случае, также равна 0,09. Поэтому все вероятности в целом таковы:
· наступление события в обоих случаях – p2 = 0,01; · ненаступление в обоих случаях – q2 = 0,81; · наступление в первом и ненаступление во втором – pq = 0,09; · наступление во втором и ненаступление в первом – qp = 0,09;
Общая вероятность всех исходов p2 + 2pq + q2 = 1,0.
Общая вероятность, таким образом, может быть алгебраически представлена как p2 + 2pq + q2 или (p + q)2.
Соответственно там, где имеются три события, вероятности будут составлять: · наступление события в трех случаях – p3 = 0,001; · ненаступление события в трех случаях – q3 = 0,729; · наступление в двух случаях и ненаступление в одном – 3p2q=0,027; · наступление в одном случае и ненаступление в двух – 3pq2 = 0,243. Общая вероятность всех исходов (p + q)3=1,0.
Подобным образом для n событий вероятности 0, 1, 2, 3, …, n того, что событие не произойдет, представлены соответственно последовательными членами разложения бинома (p + q)n. Общая вероятность всегда точно выражена единицей, поскольку (p + q) согласно определения равно 1, а из этого следует, что (p + q)n=1 каким бы не было значение n.
Там, где p=q=½, кривая биномиального распределения симметрична. Разложение (p + q)3, например, есть (p + q)3=p3 + 3p2q + 3pq2 + q3, и если p и q равны, то p3 и q3 тоже равны друг другу, а 3p2q=3pq2. Там же, где p и q неравны, кривая не будет симметрична. Если, например, p=0,1 и q=0,9, кривая будет совершенно иной.
Построить биномиальное распределение можно с помощью калькулятора.
Числовые характеристики случайной величины
Графическое представление 

- Математическое ожидание биномиального распределения M[X] = np
- Дисперсия биномиального распределения D[X] = npq
- Биномиальное, пуассоново и нормальное распределения являются главными из тех форм распределения, которыми пользуются для выполнения значительной части статистической работы.
- Проверка ряда на соответствие биномиальному закону распределения.
Источник: https://math.semestr.ru/group/binomial-distribution.php
Биномиальное распределение
Неверно писать биномиНальное, верно — «биномиальное».
Данная статья подразумевает, что Вы уже знакомы с основами статистики, в частности, что такое закон распределения и какими параметрами он характеризуется.
Биномиальное распределение — это описание «N» независимых экспериментов, результат которых всегда либо строго положителен либо строго отрицателен.
Важно, что эксперименты проводятся в одних и тех же условиях.
В качестве примера можно рассмотреть подбрасывание монеты или угадывание результатов теста, в случае с монетой положительным результатом станет «орёл» и при угадывании теста — правильный ответ.
Проводимые эксперементы должны быть независимы, это означает, что результат последующего не зависит от результата предыдущего.
№ Результат № Результат № Результат
| 1 | орёл | 2 | решка | 3 | орёл |
| 4 | решка | 5 | решка | 6 | орёл |
| 7 | орёл | 8 | решка | 9 | решка |
| 10 | орёл | 11 | решка | 12 | орёл |
| 13 | решка | 14 | решка | 15 | решка |
| 16 | орёл | 17 | орёл | 18 | решка |
| 19 | орёл | 20 | орёл | 21 | орёл |
| 22 | орёл | 23 | решка | 24 | решка |
| 25 | решка | 26 | решка | 27 | орёл |
| 28 | орёл | 29 | решка | 30 | орёл |
| 31 | решка | 32 | решка | 33 | орёл |
| Таблица 1. Испытания Бернулли. Результаты бросания монеты. Орёл выпал 16 раз |
В результате проведения ряда экспериментов мы получим вероятность положительного исходного событий, в приведённом эксперименте орёл выпал 16 раз, значит вероятность выпадения орла равна:
P(x) = Nудачно/Nвсего = 16/33 = 0.48
Формула биномиального распределения
Биномиальное распределение зависит от двух параметров: число испытаний и количество успешных событий.
Формула функции вероятности биномиального распределения:
P(X) = (nk)·pk·qn-k, (nk) — биномиальный коэффициент (nk) = (n!)/[(n-k)!k!]
И, поскольку распределение дискретное, формула функции распределения записывается как сумма вероятностей:
k ∈ [0, ⌊y⌋], F(X) = Σ(nk)·pkqn-k
Значения математического ожидания и дисперсии распределения Бернулли равны соответственно:
E[X] = np D[X] = npq
Пример
Пользуясь данными таблицы 1 оценим монетку и в следующий раз при броске загадаем нужную нам сторону 🙂 .
Предположим мы подбросим пять раз монету, чья сторона выпала больше — тот и побеждает, какова вероятность что орёл победит?
Исходные данные: n = 5 k = 3 p = 0.48
q = 0.52
Вероятности: P(n = 5, k = 3) = 120 / [2 · 6] · 0.483 · 0.522 = 0.3 P(n = 5, k = 4) = 120 / [1 · 24] · 0.483 · 0.522 = 0.14 P(n = 5, k = 5) = 120 / [1 · 120] · 0.483 · 0.522 = 0.03 F(X) = Σk=3,4,5 P(n = 5, k = k) = 0.47
Таким образом, вероятность, что орёл победит равна 47%
Источник: https://k-tree.ru/articles/statistika/analiz_dannyh/binomialnoe_raspredelenie
Биномиальное распределение случайной величины
Не все явления измеряются в количественной шкале типа 1, 2, 3 … 100500 … Не всегда явление может принимать бесконечное или большое количество различных состояний. Например, пол у человека может быть либо М, либо Ж. Стрелок либо попадает в цель, либо не попадает.
Голосовать можно либо «За», либо «Против» и т.д. и т.п. Другими словами, такие данные отражают состояние альтернативного признака – либо «да» (событие наступило), либо «нет» (событие не наступило). Наступившее событие (положительный исход) еще называют «успехом».
Эксперименты с такими данными называются схемой Бернулли, в честь известного швейцарского математика, который установил, что при большом количестве испытаний соотношение положительных исходов и общего количества испытаний стремится к вероятности наступления этого события.
Переменная альтернативного признака
Для того, чтобы в анализе задействовать математический аппарат, результаты подобных наблюдений следует записать в числовом виде. Для этого положительному исходу присваивают число 1, отрицательному – 0. Другими словами, мы имеем дело с переменной, которая может принимать только два значения: 0 или 1.
Какую пользу отсюда можно извлечь? Вообще-то не меньшую, чем от обычных данных. Так, легко подсчитать количество положительных исходов – достаточно просуммировать все значения, т.е. все 1 (успехи). Можно пойти далее, но для этого потребуется ввести парочку обозначений.
Первым делом нужно отметить, что положительные исходы (которые равны 1) имеют некоторую вероятность появления. Например, выпадение орла при подбрасывании монеты равно ½ или 0,5.
Такая вероятность традиционно обозначается латинской буквой p. Следовательно, вероятность наступления альтернативного события равна 1 — p, которую еще обозначают через q, то есть q = 1 – p.
Указанные обозначения можно наглядно систематизировать в виде таблички распределения переменной X.
Мы получили перечень возможных значений и их вероятности. Можно рассчитать математическое ожидание и дисперсию. Матожидание – это сумма произведений всех возможных значений на соответствующие им вероятности:
Вычислим матожидание, используя обозначения в таблицы выше.
Получается, что математическое ожидание альтернативного признака равно вероятности этого события – p.
Теперь определим, что такое дисперсия альтернативного признака. Дисперсия – есть средний квадрат отклонений от математического ожидания. Общая формула (для дискретных данных) имеет вид:
- Отсюда дисперсия альтернативного признака:
- Нетрудно заметить, что эта дисперсия имеет максимум 0,25 (при p=0,5).
- Стандартное отклонение – корень из дисперсии:
- Максимальное значение не превышает 0,5.
- Как видно, и математическое ожидание, и дисперсия альтернативного признака имеют очень компактный вид.
Рассмотрим ситуацию под другим углом. Действительно, кому интересно, что среднее выпадение орлов при одном бросании равно 0,5? Это даже невозможно представить. Интересней поставить вопрос о числе выпадения орлов при заданном количестве бросков.
Другими словами, исследователя часто интересует вероятность наступления некоторого числа успешных событий. Это может быть количество бракованных изделий в проверяемой партии (1- бракованная, 0 — годная) или количество выздоровлений (1 – здоров, 0 – больной) и т.д. Количество таких «успехов» будет равно сумме всех значений переменной X, т.е. количеству единичных исходов.
Случайная величина B называется биномиальной и принимает значения от 0 до n (при B = 0 – все детали годные, при B = n – все детали бракованные). Предполагается, что все значения x независимы между собой. Рассмотрим основные характеристики биномиальной переменной, то есть установим ее математическое ожидание, дисперсию и распределение.
Матожидание биномиальной переменной получить очень легко. Математическое ожидание суммы величин есть сумма математических ожиданий каждой складываемой величины, а оно у всех одинаковое, поэтому:
Например, математическое ожидание количества выпавших орлов при 100 подбрасываниях равно 100 × 0,5 = 50.
Теперь выведем формулу дисперсии биномиальной переменной. Дисперсия суммы независимых случайных величин есть сумма дисперсий. Отсюда
Стандартное отклонение, соответственно
Для 100 подбрасываний монеты стандартное отклонение количества орлов равно
И, наконец, рассмотрим распределение биномиальной величины, т.е. вероятности того, что случайная величина B будет принимать различные значения k, где 0≤ k ≤n. Для монеты эта задача может звучать так: какова вероятность выпадения 40 орлов при 100 бросках?
Чтобы понять метод расчета, представим, что монета подбрасывается всего 4 раза. Каждый раз может выпасть любая из сторон. Мы задаемся вопросом: какова вероятность выпадения 2 орлов из 4 бросков. Каждый бросок независим друг от друга.
Значит, вероятность выпадения какой-либо комбинации будет равна произведению вероятностей заданного исхода для каждого отдельного броска. Пусть О – это орел, Р – решка.
Тогда, к примеру, одна из устраивающих нас комбинаций может выглядеть как ООРР, то есть:
Вероятность такой комбинации равняется произведению двух вероятностей выпадения орла и еще двух вероятностей не выпадения орла (обратное событие, рассчитываемое как 1 — p), т.е. 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. Такова вероятность одной из устраивающих нас комбинации. Но вопрос ведь стоял об общем количестве орлов, а не о каком-то определенном порядке.
Тогда нужно сложить вероятности всех комбинаций, в которых присутствует ровно 2 орла. Ясно, все они одинаковы (от перемены мест множителей произведение не меняется). Поэтому нужно вычислить их количество, а затем умножить на вероятность любой такой комбинации. Подсчитаем все варианты сочетаний из 4 бросков по 2 орла: РРОО, РОРО, РООР, ОРРО, ОРОР, ООРР.
Всего 6 вариантов.
Следовательно, искомая вероятность выпадения 2 орлов после 4 бросков равна 6×0,0625=0,375.
Однако подсчет подобным образом утомителен. Уже для 10 монет методом перебора получить общее количество вариантов будет очень трудно.
Поэтому умные люди давно изобрели формулу, с помощью которой рассчитывают количество различных сочетаний из n элементов по k, где n – общее количество элементов, k – количество элементов, варианты расположения которых и подсчитываются. Формула сочетания из n элементов по k такова:
Подобные вещи проходят в разделе комбинаторики. Всех желающих подтянуть знания отправляю туда. Отсюда, кстати, и название биномиального распределения (формула выше является коэффициентом в разложении бинома Ньютона).
Формулу для определения вероятности легко обобщить на любое количество n и k. В итоге формула биномиального распределения имеет следующий вид.
Количество подходящих под условие комбинаций умножить на вероятность одной из них.
Для практического использования достаточно просто знать формулу биномиального распределения. А можно даже и не знать – ниже показано, как определить вероятность с помощью Excel. Но лучше все-таки знать.
Рассчитаем по этой формуле вероятность выпадения 40 орлов при 100 бросках:
Или всего 1,08%. Для сравнения вероятность наступления математического ожидания этого эксперимента, то есть 50 орлов, равна 7,96%. Максимальная вероятность биномиальной величины принадлежит значению, соответствующему математическому ожиданию.
Расчет вероятностей биномиального распределения в Excel
Если использовать только бумагу и калькулятор, то расчеты по формуле биномиального распределения, несмотря на отсутствие интегралов, даются довольно тяжело. К примеру значение 100! – имеет более 150 знаков.
Раньше, да и сейчас тоже, для вычисления подобных величин использовали приближенные формулы. В настоящий момент целесообразно использовать специальное ПО, типа MS Excel.
Таким образом, любой пользователь (даже гуманитарий по образованию) вполне может вычислить вероятность значения биномиально распределенной случайной величины.
Для закрепления материала задействуем Excel пока в качестве обычного калькулятора, т.е. произведем поэтапное вычисление по формуле биномиального распределения. Рассчитаем, например, вероятность выпадения 50 орлов. Ниже приведена картинка с этапами вычислений и конечным результатом.
Как видно, промежуточные результаты имеют такой масштаб, что не помещаются в ячейку, хотя везде и используются простые функции типа: ФАКТР (вычисление факториала), СТЕПЕНЬ (возведение числа в степень), а также операторы умножения и деления. Более того, этот расчет довольно громоздок, во всяком случаен не является компактным, т.к. задействовано много ячеек. Да и разобраться с ходу трудновато.
В общем в Excel предусмотрена готовая функция для вычисления вероятностей биномиального распределения. Функция называется БИНОМ.РАСП.
Синтаксис функции состоит из 4 аргументов:
Поля имеют следующие назначения:
Число успехов – количество успешных испытаний. У нас их 50.
Число испытаний – количество бросков: 100 раз.
Вероятность успеха – вероятность выпадения орла при одном подбрасывании 0,5.
Интегральная – указывается либо 1, либо 0. Если 0, то рассчитается вероятность P(B=k); если 1, то рассчитается функция биномиального распределения, т.е. сумма всех вероятностей от B=0 до B=k включительно.
Нажимаем ОК и получаем тот же результат, что и выше, только все рассчиталось одной функцией.
Очень удобно. Эксперимента ради вместо последнего параметра 0 поставим 1. Получим 0,5398. Это значит, что при 100 подкидываниях монеты вероятность выпадения орлов в количестве от 0 до 50 равна почти 54%. А поначалу то казалось, что должно быть 50%. В общем, расчеты производятся легко и быстро.
Настоящий аналитик должен понимать, как ведет себя функция (каково ее распределение), поэтому произведем расчет вероятностей для всех значений от 0 до 100.
То есть зададимся вопросом: какова вероятность, что не выпадет ни одного орла, что выпадет 1 орел, 2, 3, 50, 90 или 100. Расчет приведен в следующей картинке.
Синяя линия – само биномиальное распределение, красная точка – вероятность для конкретного числа успехов k.
Кто-то может спросить, а не похоже ли биномиальное распределение на… Да, очень похоже. Еще Муавр (в 1733 г.) говорил, что биномиальное распределение при больших выборках приближается к нормальному закону (не знаю, как это тогда называлось), но его никто не слушал.
Только Гаусс, а затем и Лаплас через 60-70 лет вновь открыли и тщательно изучили нормальной закон распределения. На графике выше отлично видно, что максимальная вероятность приходится на математическое ожидание, а по мере отклонения от него, резко снижается.
Также, как и у нормального закона.
Биномиальное распределение имеет большое практическое значение, встречается довольно часто. С помощью Excel расчеты проводятся легко и быстро.
Поделиться в социальных сетях:
Источник: https://statanaliz.info/statistica/teoriya-veroyatnostej/binomialnoe-raspredelenie/


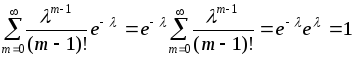
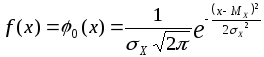
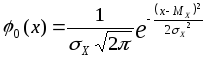
 .
.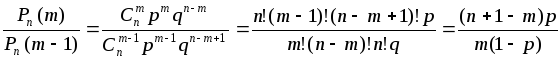
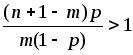 ,
,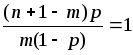 ,
,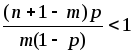 .
.





![{displaystyle mathbb {E} [Y]=np}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4449a990a54c49f0dea0dd10fe21507f002191cf)
![{displaystyle mathbb {E} left[Y^{2}right]=np(q+np)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0487942f4eef0b21afe6b6fce2d94ff3a357e58a)
![{displaystyle mathbb {D} [Y]=npq}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4258ca89d2fbdbe66aa2fb66a65574cfbfe1e7)