Двумерной называют случайную величину
, возможные значения
которой есть пары чисел
. Составляющие
и
, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку
на плоскости
либо как случайный вектор
.
Дискретной называют двумерную величину, составляющие которой дискретны.
Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих
Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.
Закон
распределения дискретной двумерной случайной величины может быть задан:
а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;
б) аналитически, например в виде функции распределения.
Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность
, надо просуммировать
вероятности столбца
. Аналогично сложив
вероятности строки
получим вероятность
.
Пусть
составляющие
и
дискретны и имеют соответственно следующие
возможные значения:
;
.
Условным распределением составляющей
при
(j сохраняет одно и то же
значение при всех возможных значениях
) называют совокупность
условных вероятностей:
Аналогично
определяется условное распределение
.
Условные
вероятности составляющих
и
вычисляют соответственно по формулам:
Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Ковариация (корреляционный момент)
Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки
.
Ковариацию
(корреляционный момент) можно найти по формуле:
Свойства ковариации
Свойство 1.
Ковариация двух независимых случайных величин равна нулю.
Свойство 2.
Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.
Свойство 3.
Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.
Коэффициент корреляции
Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.
Формула коэффициента корреляции:
Две
случайные величины
и
называют коррелированными, если их коэффициент
корреляции отличен от нуля.
и
называют некоррелированными величинами, если
их коэффициент корреляции равен нулю
Свойства коэффициента корреляции
Свойство 1.
Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.
Свойство 2.
Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.
Свойство 3.
Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Линейная регрессия
Рассмотрим
двумерную случайную величину
, где
и
– зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины
в виде линейной функции величины
:
где
и
– параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.
Линейная
средняя квадратическая регрессия
на
имеет вид:
Коэффициент
называют
коэффициентом регрессии
на
, а прямую
называют
прямой среднеквадратической регрессии
на
.
Аналогично
можно получить прямую среднеквадратической регрессии
на
:
Смежные темы решебника:
- Двумерная непрерывная случайная величина
- Линейный выборочный коэффициент корреляции
- Парная линейная регрессия и метод наименьших квадратов
Задача 1
Закон
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.
Требуется:
—
определить одномерные законы распределения случайных величин X и Y;
— найти
условные плотности распределения вероятностей величин;
—
вычислить математические ожидания mx и my;
—
вычислить дисперсии σx и σy;
—
вычислить ковариацию μxy;
—
вычислить коэффициент корреляции rxy.
| xy | 3 | 5 | 8 | 10 | 12 |
| -1 | 0.04 | 0.04 | 0.03 | 0.03 | 0.01 |
| 1 | 0.04 | 0.07 | 0.06 | 0.05 | 0.03 |
| 3 | 0.05 | 0.08 | 0.09 | 0.08 | 0.05 |
| 6 | 0.03 | 0.04 | 0.04 | 0.06 | 0.08 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Задана
дискретная двумерная случайная величина (X,Y).
а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X; в) построить регрессию случайной величины X на Y; г) найти коэффициент ковариации; д) найти
коэффициент корреляции.
| Y | X | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 30 | 0.05 | 0.03 | 0.02 | 0.01 | 0.01 |
| 40 | 0.03 | 0.02 | 0.02 | 0.04 | 0.01 |
| 50 | 0.05 | 0.03 | 0.02 | 0.02 | 0.01 |
| 70 | 0.1 | 0.03 | 0.04 | 0.03 | 0.01 |
| 90 | 0.1 | 0.04 | 0.01 | 0.07 | 0.2 |
Задача 3
Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.
|
x y |
1 | 2 | 3 |
| 1.5 | 0.03 | 0.02 | 0.02 |
| 2.9 | 0.06 | 0.13 | 0.03 |
| 4.1 | 0.4 | 0.07 | 0.02 |
| 5.6 | 0.15 | 0.06 | 0.01 |
Задача 4
Двумерная
случайная величина (X,Y) распределена по закону
| XY | 1 | 2 |
| -3 | 0,1 | 0,2 |
| 0 | 0,2 | 0,3 |
| -3 | 0 | 0,2 |
Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.
Задача 5
Случайные
величины ξ и η имеют следующий совместный закон распределения:
P(ξ=1,η=1)=0.14
P(ξ=1,η=2)=0.18
P(ξ=1,η=3)=0.16
P(ξ=2,η=1)=0.11
P(ξ=2,η=2)=0.2
P(ξ=2,η=3)=0.21
1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.
2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).
3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}
4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.
Задача 6
Дан закон
распределения двумерной случайной величины (ξ,η):
| ξ=-1 | ξ=0 | ξ=2 | |
| η=1 | 0,1 | 0,1 | 0,1 |
| η=2 | 0,1 | 0,2 | 0,1 |
| η=3 | 0,1 | 0,1 | 0,1 |
1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания Mξ,
Mη и дисперсии Dξ, Dη
2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).
3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?
4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти Mγ и Dγ.
Задача 7
Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.
| XY | 1 | 2 | 4 |
| -2 | 0,25 | 0 | 0,25 |
| 1 | 0 | 0,25 | 0 |
| 3 | 0 | 0,25 | 0 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 8
Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.
| YX | -1 | 1 |
| -1 | 0,4 | 0,1 |
| 1 | 0,2 | 0,3 |
Задача 9
Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:
| X=-3 | X=0 | X=1 | |
| Y=-2 | 0,3 | ? | 0,1 |
| Y=1 | 0,1 | 0,1 | 0,2 |
Задача 10
Совместный
закон распределения пары
задан таблицей:
| xh | -1 | 0 | 1 |
| -1 | 1/12 | 1/4 | 1/6 |
| 1 | 1/4 | 1/12 | 1/6 |
Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.
Задача 11
Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции rxy?
| X | 20 | 25 | 30 | 35 |
| P | 0.1 | 0.1 | 0.4 | 0.4 |
и
Задача 12
Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):
| XY | 0 | 1 | 2 |
| -1 | ? | 0,1 | 0,2 |
| 1 | 0,1 | 0,2 | 0,3 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 13
Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:
| ξη | -1 | 1 | 2 |
| 0 | 1/7 | 2/7 | 1/7 |
| 1 | 1/7 | 1/7 | 1/7 |
Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?
Задача 14
Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.
| XY | 2,3 | 2,9 | 3,1 | 3,4 |
| 0,2 | 0,15 | 0,15 | 0 | 0 |
| 2,8 | 0 | 0,25 | 0,05 | 0,01 |
| 3,3 | 0 | 0,09 | 0,2 | 0,1 |
Задача 15
Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.
| xy | 1 | 4 |
| -10 | 0,1 | 0,2 |
| 0 | 0,3 | 0,1 |
| 20 | 0,2 | 0,1 |
Задача 16
Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:
а) законы
распределения ее компонент и их числовые характеристики;
b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.
с)
ковариацию и коэффициент корреляции случайных величин X и Y;
d) составить матрицу ковариаций и матрицу корреляций;
e) вероятность попадания в область, ограниченную линиями y=16-x2 и y=0.
f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.
| XY | -1 | 0 | 1 | 2 |
| -1 | 0 | 1/6 | 0 | 1/12 |
| 0 | 1/18 | 1/9 | 1/12 | 1/9 |
| 2 | 1/6 | 0 | 1/9 | 1/9 |
Задача 17
Совместный
закон распределения случайных величин X и Y задан таблицей:
|
XY |
0 |
1 |
3 |
|
0 |
0,15 |
0,05 |
0,3 |
|
-1 |
0 |
0,15 |
0,1 |
|
-2 |
0,15 |
0 |
0,1 |
Найдите:
а) закон
распределения случайной величины X и закон распределения
случайной величины Y;
б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.
Задача 18
Известен
закон распределения двумерной случайной величины (X,Y).
а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);
б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;
в)
построить поле распределения и линию регрессии Y по X и X по Y;
г)
вычислить корреляционный момент (коэффициент ковариации) μxy и
коэффициент корреляции rxy.
|
|
5 | 20 | 35 |
| 100 | — | — | 0.05 |
| 115 | — | 0.2 | 0.15 |
| 130 | 0.15 | 0.35 | — |
| 145 | 0.1 | — | —- |
-
Математическое ожидание двумерной случайной величины. Свойства
Математическим
ожиданием двумерной случайной величины
называется совокупность двух
математических ожиданий М[Х], М[Y],то
есть упорядоченных пар М[Х], М[Y],которые
определяются равенствами:
Если Х, У непрерывная
случайная величина, то тогда
Свойства
–точно такие же как и у мат ож случ
величины, но эти свойства для функций
Свойство
1. Математическое
ожидание постоянной равно самой этой
постоянной.
М(С)=С×1=С
Свойство
2. Математическое
ожидание алгебраической суммы случайных
величин равно алгебраической суме их
математических ожиданий.
Ограничимся
доказательством этого свойства только
для суммы двух дискретных случайных
величин, т.е. докажем, что
Под
суммой двух дискретных сл. Величин
понимается сл. Величина, которая
принимает значения с
вероятностями
По
определению
Но
где вероятность
события ,
вычисленная при условии, что .
В правой части последнего равенства
перечислены все случаи появления
события ,
поэтому равна
полной вероятности появления события ,
т.е. .
Аналогично .
Окончательно имеем
Свойство
3. Математическое
ожидание произведения двух независимых
случайных величин равно произведению
их математических ожиданий.
|
У |
|
|
… |
|
|||
|
Q |
|
|
… |
|
|||
|
Х |
|
|
… |
|
|||
|
Р |
|
|
… |
|
|||
-
Зависимые и независимые двумерные случайные величины
Случайные величины
X
и Y
называются независимыми, если их
совместная функция распределения
F(x,y)
представляется в виде произведения
функций распределения

и
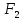
этих случайных величин, т.е.

В противном случае,
при невыполнении равенства, случайные
величины X
и Y
называются зависимыми.
т.е для независимых
непрерывных случайных величин X
и Y
их совместная плотность

произведению плотностей вероятности
этих случайных величин .
Независимость
случайных величин X
и Y
означает, что условные плотности
вероятности каждой из них совпадают с
соответствующими « безусловными»
плотностями, т.е.
Зависимость между
двумя случайными величинами называется
вероятной (стохастической или
статистической ) , если каждому значению
одной из них соответствует определенное
(условное) распределение другой .
Если случайные
величины X
и Y
независимы, то линии регрессии X
по Y
и Y
по X
параллельны координатным осям Оx
и Оy.
-
Ковариация и коэффициент корреляции.
Ковариация –
математическое ожидание от произведения
определения средних величин.
Для дискретной
случайной величины:
Для непрерывных
случайных величин:
Свойства ковариации:
-
Ковариация
симметрична
-
Постоянный
множитель можно выносить за знак
ковариации k(cx,
y) = k(x,cy) = ck(x,y) -
Ковариация не
изменится если к случайным величинам
добавить случайные величины k(x+a,
y)
= k(x,
y
+b)
= k(x+a,
y+b) a,b
R
-
Дисперсия случайной
величины – это ковариация случайной
величины с самой собой D(x)
=
-
Дисперсия суммы
= сумме дисперсий
удвоенная ковариация
D(x
6.Если случайные
величины независимы, то ковариация = 0
7. Ковариация по
абсолютной величине не превосходит
произведение средних квадратических
отклонений.
|
Коэффициент
корреляции двух случайных величин –
отношение их ковариации к произведению
средних квадратических отклонений
этих величин:
Свойства коэффициента
корреляции:
-
-
Для независимых
случайных величин (x,
y
– независимы)
=0
-
Если x
и y
связаны линейной функциональной
зависимостью
Y
= ax
+ b,
то если

(a>0)
то это прямая линейная зависимость ,
если
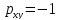
это обратная линейная зависимость
(а
справедливо и
обратное утверждение т.е. если модуль
, то между величинами x,
y
существует линейная функциональная
зависимость
Соседние файлы в папке Экзамен
- #
- #
Пусть двумерная непрерывная случайная величина задана такой плотностью:
Найдём математическое ожидание по следующим формулам:
Подставим данную выше плотность в эти формулы и вычислим интегралы, сразу видим что $M xi$ и $M eta$ отличаются только изменением $x$ на $y$, поэтому результат будет тот же в обоих случаях. Хочу сразу напомнить, что при нахождении двойного интеграла, сначала берётся интеграл по внутренней переменной, а потом по внешней. Тогда для упрощения вычислений, расписываем всё только для первого, а второй будет высчитываться аналогически (и также в следующих случаях):
После нахождения математического ожидания найдём дисперсию, для этого нам понадобятся следующие формулы:
Видим, что мы уже нашли $M xi$ и $M eta$ надо найти $M xi^2$ и $M eta^2$, в этом случае используем формулы:
Подставив плотность и вычислив интегралы, мы получим:
Теперь полученные данные можно подставлять в формулу для дисперсии:
Найдём ковариацию по следующей формуле:
Опять видим, что некоторые данные $M xi$ и $M eta$ у нас уже есть, а надо ещё найти $M ( xi eta)$, в этом нам поможет следующая формула:
Опять подставляем данную плотность и вычисляем соответствующие интегралы:
Теперь, имея уже все данные, можем подставлять их в формулу для ковариации:
Ковариационная матрица будет такая:
Ещё можем вычислить корреляцию. Вот формула для её нахождения:
Видим, что для нахождения корреляции, нам ещё надо найти среднее квадратическое отклонение, для этого используем следующие формулы и потом подставим все полученные данные в формулу для корреляции:
Материалы по теме:
- Корень с комплексного числа. Тригонометрическая форма.
- Смешанное, векторное и скалярное произведение векторов
- Нахождение асимптот функции.
- Экстремумы функции
Загрузка…



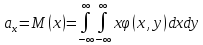
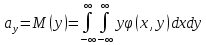


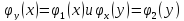
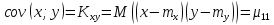



 R
R
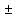
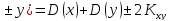

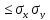
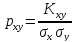

 =0
=0












