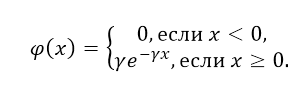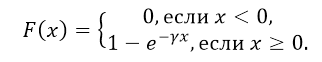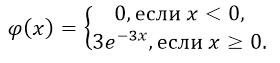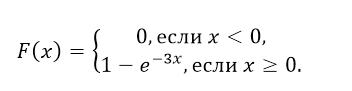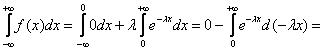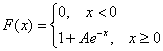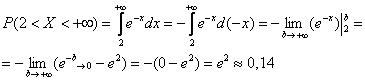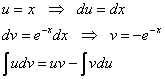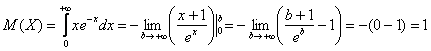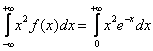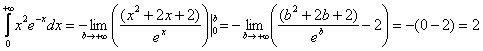Показательное распределение
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины
, которое описывается плотностью:
где
–
постоянная положительная величина.
Показательное
распределение определяется одним параметром
. Эта особенность распределения указывает на
его преимущество по сравнению с распределениями, зависящими от большего числа
параметров. Обычно параметры неизвестны и приходится находить их оценки
(приближенные значения); разумеется, проще оценить один параметр, чем два или три.
Примером непрерывной случайной величины, распределенной по показательному
закону, может служить время между появлениями двух последовательных событий
простейшего потока.
Функция распределения
показательного закона:
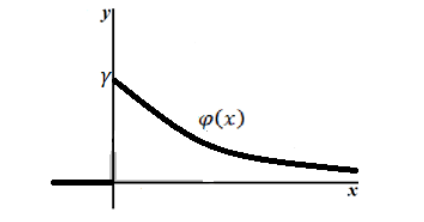
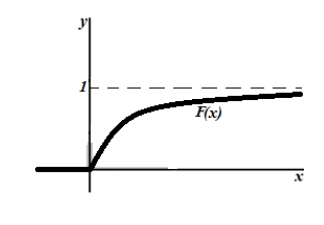
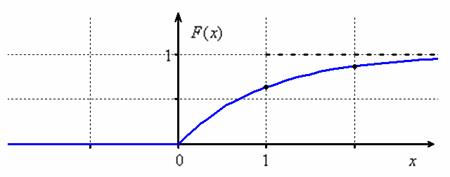
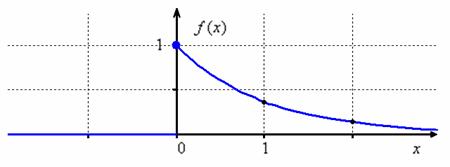
Графики плотности и
функции распределения показательного закона изображены на рисунке.
Вероятность попадания в
интервал
непрерывной
случайной величины
, распределенной по показательному закону:
Числовые характеристики показательного (экспоненциального) распределения
Математическое ожидание случайной величины, распределенной по показательному закону:
Дисперсия случайной величины, распределенной по показательному закону:
Среднее квадратическое отклонение случайной величины,
распределенной по показательному закону:
Коэффициенты асимметрии и эксцесса
для показательного распределения:
Таким
образом, математическое ожидание и среднее квадратическое
отклонение экспоненциального распределения равны между собой.
Показательный закон
распределения играет большую роль в теории массового обслуживания и теории
надежности. Так, например, интервал времени
между
двумя соседними событиями в простейшем потоке имеет показательное распределение
с параметром
–
интенсивностью потока.
При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.
Смежные темы решебника:
- Непрерывная случайная величина
- Нормальный закон распределения случайной величины
- Равномерный закон распределения случайной величины
Примеры решения задач
Пример 1
Случайная величина
задана функцией распределения
Найдите математическое
ожидание и среднее квадратическое отклонение этого
распределения.
Найдите вероятность того,
что случайная величина примет значение от 0,2 до 1.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Математическое
ожидание случайной величины, распределенной по показательному закону:
Среднее
квадратическое отлонение:
Вероятность того, что
случайная величина примет значение от 0,2 до 1
Ответ
.
Пример 2
На шоссе установлен контрольный пункт для
проверки технического состояния автомобилей. Найти математическое ожидание и
среднее квадратическое отклонение случайной величины T – время ожидания
очередной машины контролером, если поток машин простейший и время (в часах)
между прохождениями машин через контрольный пункт распределено по
показательному закону f(t)=5e-5t.
Указание: Время ожидания машины
контролером и время прохождения машин через контрольный пункт распределены
одинаково.
Решение
В нашем случае
параметр показательного распределения
Математическое
ожидание:
Дисперсия:
Среднее
квадратическое отклонение:
Ответ:
Пример 3
Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите математическое ожидание M(X), дисперсию D(X),
среднее квадратическое отклонение σ(X), моду xmod, медиану xmed , если известно, что
случайная величина X имеет показательное распределение с параметром λ=1.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Плотность
распределения случайной величины
, распределенной по
показательному закону:
Функция
распределения:
Построим
графики дифференциальной и интегральной функций распределения:
График дифференциальной функции распределения
График интегральной функции распределения
Математическое
ожидание показательно распределенной случайной величины
:
Дисперсия:
Среднее
квадратическое отклонение:
найдем, исходя из условия:
Пример 4
Случайная
величина
распределена показательно с дисперсией 0,25.
Найти математическое ожидание и вероятность попадания
в интервал (0,5;1).
Решение
Дисперсия
случайной величины, распределенной по показательному закону:
Математическое
ожидание случайной величины, распределенной по показательному закону:
Вероятность
попадания в интервал
непрерывной случайной величины
, распределенной по
показательному закону:
В нашем
случае:
Ответ:
Задачи контрольных и самостоятельных работ
Задача 1
Время
безотказной работы двигателя автомобиля распределено по показательному закону.
Известно, что среднее время наработки двигателя на отказ между техническим
обслуживанием 100 ч. Определить вероятность безотказной работы двигателя за 80
ч.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Среднее
время работы элемента, входящего в пожарно-техническое устройство, равно 1000
часов. Определить вероятность того, что элемент будет работать от 950 до 1150
часов, если время работы элемента распределено по показательному закону.
Задача 3
Вероятность
безотказной работы элемента распределена по экспоненциальному закону
f(t)=e-0.05t
Найти
вероятность того, что в результате испытания случайная величина попадет в
интервал (11;35). Найти характеристики данного распределения случайной
величины.
Задача 4
Непрерывная
случайная величина X задана интегральной функцией распределения
Найти
постоянную C, математическое ожидание случайной величины X,
вероятность попадания случайной величины в интервал [2;4].
Задача 5
Время
между отказами прибора распределено по показательному закону со средним
значением 25 часов. Определить математическое ожидание и дисперсию времени
безотказной работы автомобиля. Найти вероятность того, что очередной отказ
произойдет не позднее 15 часов.
Задача 6
Время
безотказной работы телевизора определенной модели описывается показательным (экспоненциальным)
законом распределения с постоянной λ. Что вероятнее, его безотказная работа в
промежутке времени [x1,x2]
или [x3,x4]? Записать
функции f(x),F(x) и построить их графики.
λ=1/10, x1=3, x2=5, x3=4, x4=8
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 7
Испытывают
два независимо работающих элемента. Длительность времени t безотказной
работы первого элемента имеет показательное распределение с параметром 0,02,
второго -показательное распределение с параметром 0,06. Найдите вероятность
того, что за время длительностью t=6 ч откажет только один
элемент.
Задача 8
Среднее
время работы каждого из трех элементов, входящих в техническое устройство,
равно T=850 часов. Для безотказной работы устройства необходима безотказная
работа хотя бы одного из трех этих элементов. Определить вероятность, что
устройство будет работать от t1=750 до t2=820 часов, если время
работы каждого из трех элементов независимо и распределено по показательному
закону.
Задача 9
Время
устранения повреждения на канале связи T -случайная величина,
распределенная по закону f(t)=λe-λt (t≥0). Среднее время
восстановления канала — 10 минут. Определить вероятность того, что на
восстановление канала потребуется от 5 до 10 минут.
Задача 10
Дана плотность
распределения случайной величины X.
По какому
закону распределения случайная величина? Найти математическое ожидание,
дисперсию, функцию распределения?
Задача 11
Время
безотказной работы механизма подчинено показательному закону с плотностью
распределения вероятностей f(t)=0.04e-0.04t при t > 0 (t –
время в часах). Найти вероятность того, что механизм проработает безотказно не
менее 100 часов.
Задача 12
Длительность телефонного разговора
является случайной величиной, распределенной по показательному закону.
Известно, что средняя длительность телефонного разговора равна 9 минутам. Найти
вероятность того, что разговор будет длиться:
а) не более 5 минут.
б) более 5 минут.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 13
Случайная величина ξ подчинена
показательному закону с параметром λ=5:
Найдите вероятность того, что
случайная величина ξ примет значение меньшее, чем ее математическое ожидание.
Задача 14
Случайная
величина ξ имеет плотность вероятностей (показательное распределение)
Найдите
вероятность P{ξ>Mξ}
Задача 15
Время T
(минут), затрачиваемое клиентами парикмахерской в ожидании своей очереди,
удовлетворяет показательному распределению с параметром λ=0,05. Какова
вероятность того, что время ожидания превысит 25 минут и каково среднее время
ожидания.
Задача 16
Время T (час),
необходимое на ремонт легкового автомобиля удовлетворяет показательному
распределению с параметром λ=0,2. Какова вероятность того, что время ремонта
одного автомобиля не превысит 6 часов, и сколько часов в среднем затрачивается
на ремонт одного автомобиля.
Задача 17
Время
ожидания у бензоколонки автозаправочной станции является случайной величиной X,
распределенной по показательному закону, со средним временем ожидания, равным t0. Найти вероятности
следующих событий:
Задача 18
Случайная
величина X задана показательным законом распределения и
числовыми значениями параметров M(X)=3 и σx=3.
Требуется:
1) найти
функцию плотности f(x).
2) найти
вероятность попадания СВ X в указанный интервал [a,b]=[2,4].
Задача 19
Случайная
величина ξ задана функцией распределения
Найдите
математическое ожидание и среднее квадратическое отклонение этого
распределения.
Задача 20
Случайная величина ξ распределена по
показательному закону с параметром λ=0,3. Найдите математическое ожидание и
среднее квадратическое отклонение этой случайной величины.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Непрерывная
случайная величина Х,
функция плотности которой задается
выражением
называется случайной величиной,
имеющей показательное,
или экспоненциальное, распределение.
В отличие от нормального
распределения, показательный закон
определяется только одним параметром λ.
В этом его преимущество, так как обычно
параметры распределения заранее не
известны и их приходится оценивать
приближенно. Понятно, что оценить один
параметр проще, чем несколько.
Найдем
функцию распределения показательного
закона:
Теперь
можно найти вероятность попадания
показательно распределенной случайной
величины в интервал (а, b):
. Значения
функции е-х можно
найти из таблиц.
Математическое
ожидание
Проводя
интегрирование по частям и учитывая,
что при x→∞ e—x стремиться
к нулю быстрее, чем возрастает любая
степень x ,
находим:
29) Показательное распределение. Дисперсия.
Непрерывная
случайная величина Х,
функция плотности которой задается
выражением
называется случайной величиной,
имеющей показательное,
или экспоненциальное, распределение.
В отличие от нормального
распределения, показательный закон
определяется только одним параметром λ.
В этом его преимущество, так как обычно
параметры распределения заранее не
известны и их приходится оценивать
приближенно. Понятно, что оценить один
параметр проще, чем несколько.
Найдем
функцию распределения показательного
закона:
Теперь
можно найти вероятность попадания
показательно распределенной случайной
величины в интервал (а, b):
Значения
функции е-х можно
найти из таблиц.
Дисперсию
случайной
величины определяем по формуле:
30) Функции случайных величин. Примеры.
Примеры
одномерных величин. Число сокращений сердца за
одну минуту, полученное при регистрации,
— дискретная одномерная величина. Артериальное
давление крови,
зарегистрированное в данный момент времени,
— значение одномерной непрерывной
случайной величины.
Если
каждому возможному значению случ.величины Х
соответствует
одно возможное значение случ.
величины Y,то Y называют функцией
случайного аргумента Х: Y =
φ(X).
Выясним,
как найти закон распределения функции
по известному закону распределения
аргумента.
1) Пусть
аргумент Х –
дискретная случайная величина, причем
различным значениям Х
соответствуют
различные значения Y.
Тогда вероятности соответствующих
значений Х и Y
равны.
Пример
1.
Ряд распределения для Х имеет
вид:
Х
5 6
7 8
р
0,1 0,2 0,3 0,4
Найдем
закон распределения функции Y = 2X²
— 3:
Y 47
69 95 125
р
0,1 0,2 0,3 0,4
(при
вычислении значений Y в
формулу, задающую функцию, подставляются
возможные значения Х).
2) Если
разным значениям Х могут
соответствовать одинаковые значения Y,
то вероятности значений аргумента, при
которых функция принимает одно и то же
значение, складываются.
Пример
2.
Ряд распределения для Х имеет
вид:
Х
0 1
2 3
р
0,1 0,2 0,3 0,4
Найдем
закон распределения функции Y = X²
— 2Х:
Y -1
0 3
р
0,2 0,4 0,4
(так
как Y =
0 при Х
= 0
и Х
= 2,
то р(Y = 0)
= р( Х =
0) + р(Х =
2) = 0,1 + 0,3 = 0,4 ).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Показательное распределение
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Отметим здесь основные понятия и формулы, связанные с показательным распределением непрерывной случайной величины $X$ не вдаваясь в подробности их вывода.
Определение 1
Показательным или экспоненциальным распределения непрерывной случайной величины $X$ называется распределение, плотность которого имеет вид:
Рисунок 1.
где $gamma $ — положительная константа.
График плотности показательного распределения имеет вид (рис. 1):
Рисунок 2. График плотности показательного распределения.
Функция показательного распределения
Как нетрудно проверить, функция показательного распределения имеет вид:
Рисунок 3.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
где $gamma $ — положительная константа.
График функции показательного распределения имеет вид:
Рисунок 4. График функции показательного распределения.
Вероятность попадания случайной величины при показательном распределении
Вероятность попадания непрерывной случайной величины в интервал $(alpha ,beta )$ при показательном распределении вычисляется по следующей формуле:
Математическое ожидание: $Mleft(Xright)=frac{1}{gamma }.$
Дисперсия: $Dleft(Xright)=frac{1}{{gamma }^2}.$
Среднее квадратическое отклонение: $sigma left(Xright)=frac{1}{gamma }$.
Пример задачи на показательное распределение
Пример 1
Случайная величина $X$ подчиняется экспоненциальному закону распределения. На участке области определения $left[0,infty )right.$ случайная величина $X$ имеет плотность вида $varphi left(xright)=alpha e^{-3x}$.
-
Найти плотность распределения и построить её график.
-
Найти функцию распределения и построить её график.
-
Найти вероятность того, что случайная величина попадет в интервал $(0,2;;0,4)$.
-
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение данного распределения.
Решение:
- Так как случайная величина подчиняется показательному закону распределения, то $alpha =3.$ Таким образом, плотность данного распределения будет иметь вид:
Рисунок 5.
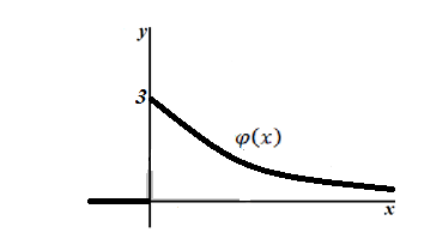
Построим её график. Максимальное значения функция плотности распределения достигнет в точке $left(0,gamma right)=(0,3)$
Рисунок 6.
- Так как $gamma =3$, то по формуле функции показательного распределения, функция распределения в нашем случае будет иметь вид:
Рисунок 7.
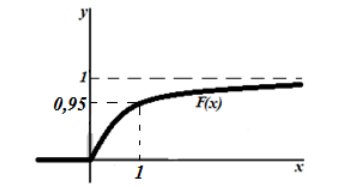
При $x=1, Fleft(1right)=1-e^{-3}=1-0,05=0,95$, получаем график
Рисунок 8.
- Для нахождения искомой вероятности будем пользоваться следующей формулой:
[Pleft(alpha Получим:
[Pleft(0,2Для нахождения значений функции $y=e^{-x}$ существуют специальные таблицы, из них легко находим, что $e^{-0,6}=0,549, e^{-1,2}=0,302$. Значит:
[Pleft(0,2
[Mleft(Xright)=sigma left(Xright)=frac{1}{gamma }=frac{1}{3}.] [Dleft(Xright)=frac{1}{{gamma }^2}=frac{1}{9}.]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 20.02.2023
Содержание:
- Показательное распределение
- Задача с решением
Во многих теоретических и практических вероятностных задачах, связанных, например, с анализом надежности технических систем, исследовании случайных промежутков времени между редкими событиями и др., используется показательный (экспоненциальный) закон распределения.
Показательный закон распределения непрерывной случайной величины описывается плотностью вида
Здесь 


В соответствии с определением (4.6) найдем функцию распределения показательного закона:
Функция распределения (5.27) имеет характер восходящей экспоненты, которая стремится к 1 при 
Вероятность попадания экспоненциально распределенной случайной величины 

Определим теперь числовые характеристики показательного распределения.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
На основании (4.19) математическое ожидание непрерывной случайной величины с плотностью (5.26) равно:
Применяя к (5.29) интегрирование по частям при 
Для получения дисперсии воспользуемся выражением (4.29):
Интегрирование по частям позволяет преобразовать это выражение к виду:
Таким образом, математическое ожидание и дисперсия экспоненциально распределенной случайной величины определяются обратной величиной и квадратом обратной величины параметра 


Легко убедиться в том, что и моменты высших порядков также являются функциями от 
которые могут быть использованы для нахождения значений первых четырех начальных моментов показательного распределения. Согласно (4.37) эти значения равны:
Из (5.32) следует, что 

Центральные моменты показательного распределения могут быть получены с помощью выражений (4.41), связывающих центральные и начальные моменты. Применяя (5.32) к (4.41), получим

Значения центральных моментов (5.33) позволяют найти коэффициенты асимметрии (4.32) и эксцесса (4.33):
Возможно вам будут полезны данные страницы:
В среде Mathcad показательному закону распределения соответствуют встроенные функции, в названии имеющие корневое слово 









Рис. 5.4. Вид плотностей и функции показательного распределения
Плотность (5.26) имеет характер ниспадающей кривой (экспоненты), асимптотически приближающейся к оси 



Функция 
Показательное распределение
В этом подразделе будет рассмотрено показательное распределением времени , которое встречается, когда имеют дело с распределением времени совершенно случайных событий.
Задача с решением
Найти закон распределения времени перегорания лампочки, если вероятность 
Решение:
Введем обозначение событий:





Очевидно, что
Пусть 
Таким образом, 




Тогда
При малых 

Разделим части уравнения на 
Вспомнив, что 




Итак, показательным (экспоненциальным) называют распределение непрерывной случайной величины 

где 
Графики плотности вероятности (рис. 2.13, 
Показательное распределение, обозначаемое 
одним из основных понятий которой является функция надежности.
Также закон показательного распределения используется в системах массового обслуживания.
В частности, по показательному закону изменяется промежуток времени между двумя последовательными событиями или соседними заявками для простейших потоков в теории массового обслуживания (см. подразд. 2.4).
Пусть непрерывная случайная величина 
Таким образом, математическое ожидание показательного распределения равно величине, обратной параметру 




Найдем дисперсию:
откуда
Получили, что показательное распределение определяется всего одним параметром
Действительно, замеченная нами особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров. Обычно параметры неизвестны и в математической статистике приходится находить их оценки (приближенные значения). Очевидно, проще оценить один параметр, чем два, три и т.д.
Найдем вероятность попадания 



Лекции:
- Дифференциальные уравнения первого порядка. Понятие о методе Рунге—Кутта
- Усеченный конус. Поверхность усеченного конус
- Функция Лагранжа
- Признак Даламбера. Признак Коши. Критерий Коши сходимости ряда
- Решение дифференциальных уравнений
- Формула Ньютона-Лейбница
- Найти первую и вторую производные функции
- Производная котангенса: пример решения
- Дифференцируемая функция: пример решения
- Действия над матрицами
2.5.2. Показательное распределение вероятностей
Показательным или экспоненциальным называют распределение, которое характеризуется следующей функцией плотности:
, где
Убедимся в том, что перед нами не «подделка». Поскольку и несобственный интеграл:
, то функция
действительно
задаёт закон распределения непрерывной случайной величины.
Используя стандартный алгоритм, легко найти функцию распределения данной случайной величины:
,
и опять же через общие формулы нетрудно получить числовые характеристики
экспоненциального распределения:
Большим достоинством показательного распределения является тот факт, что оно определяется всего лишь одним параметром. Всего лишь
одним, Карл! И по этой причине нам достаточно разобрать одну-единственную задачу, проще всего для . Как-то так получилось, что во всех примерах параграфа Равномерное распределение мы начинали с функции
, и поэтому для разнообразия зайдём в лес с другой
стороны:
Задача 117
Непрерывная случайная величина задана своей функцией распределения:
Требуется:
1) определить коэффициент ;
2) найти плотность распределения вероятностей ;
3) схематично построить графики функций и
;
4) вычислить математическое ожидание и дисперсию ;
5) определить вероятность того, что примет значение из интервала
.
Одним словом, обычная задача на НСВ, бессмысленная и беспощадная, заметьте, кстати,
что в условии ничего не сказано о том, что эта величина распределена по экспоненциальному закону.
Решаем:
1) В силу непрерывности функции распределения:
–
при этом и только при этом значении предложенная функция задаёт закон распределения непрерывной случайной величины:
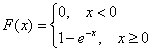
соответствует шаблону для
, таким образом, мы имеем дело с экспоненциальным
распределением.
2) Найдём функцию плотности распределения:
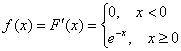
полностью соответствует шаблону.
На всякий случай производная сложной функции: .
3) Условие допускает схематическое построение графиков, но зачем занижать планку? Даже при их ручном построении
не составляет никакого труда найти пару дополнительных точек и проявить маломальскую аккуратность.
Вычислим пару опорных значений: ,
и простенький предел
. Таким образом, прямая
(изображена пунктиром) является
горизонтальной асимптотой для графика при
:
Показательное распределение нашло широкое применение в прикладных задачах, и пока чертёж не уехал вверх, приведу конкретный пример.
Пусть на промежутке переменная «икс» обозначает время и в момент
времени начинает
эксплуатироваться некий прибор, например, обычная лампочка. Тогда экспоненциальная случайная величина характеризует время работы лампочки до
перегорания. И тогда функция описывает вероятность того, что лампочка проработает
МЕНЬШЕ, чем прошедшее время . По понятным причинам при увеличении
эта вероятность стремится к
единице, что хорошо иллюстрирует вышеприведённый график.
Кстати, о чём идёт речь в 5-м пункте условия? В контексте рассматриваемого примера, нам нужно найти – вероятность того, что лампочка проработает
более 2 тыс. часов (значения, естественно, условные). Давайте сразу и вычислим эту вероятность:
5)
Ситуацию наглядно иллюстрирует чертёж ПЛОТНОСТИ распределения вероятностей:
Площадь между графиком и осью абсцисс равна единице (проверено в начале
параграфа), и значительная часть этой площади (а именно, ) сосредоточена на промежутке от 0 до 2.
Применительно к «ламповому» примеру, определённый интеграл 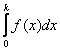
тыс. часов. В
частности, как раз:
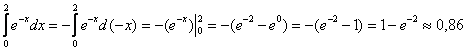
Соответственно, несобственный интеграл 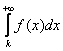
тыс. часов, и
Пункт 5) можно решить вторым способом:
4) Вычислим математическое ожидание и дисперсию.
Несмотря на то, что существуют готовые формулы для расчёта этих характеристик, решать, конечно же, будем подробно. По формуле математического ожидания:
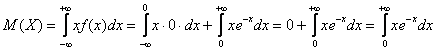
Сначала удобно найти неопределенный интеграл:
Вспоминаем интегрирование по частям:
–
произвольную константу приплюсовывать не надо, т.к. она всё равно сократится.
Таким образом:
Примечание: , т.к. знаменатель более высокого порядка роста.
Дисперсию вычислим по формуле , и из избушки на курьих ножках появляется следующий
интеграл:
Как и в случае с матожиданием, сначала проясним первообразную:
По канонам жанра тут нужно дважды интегрировать по частям, но решение облегчается тем, что после 1-го применения формулы мы сталкиваемся с только
что решённым интегралом:
Таким образом, несобственный интеграл:
Примечание: по той же самой причине.
Таким образом:
Проверим полученные результаты с помощью готовых формул:
Готово.
Показательное распределение нашло широкое применение в теории надёжности, этой теме, в частности, посвящены отдельные главы
учебного пособия В.Е. Гмурмана. Помимо лампочек и более грустных примеров существуют и другие приложения. Так, например, в простейшем потоке событий время ожидания каждого последующего события распределено именно по экспоненциальному закону.
Ну а сейчас пришло время зажечь новые огни и перейти к кульминационному параграфу под названием:


| Оглавление |
Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин