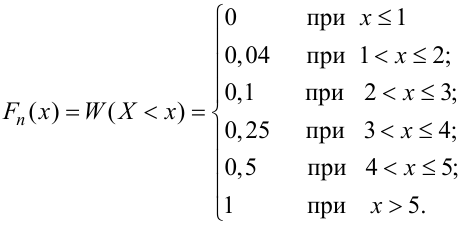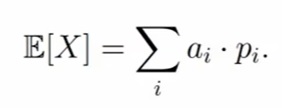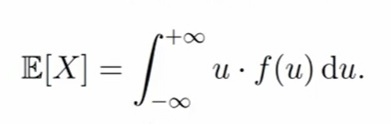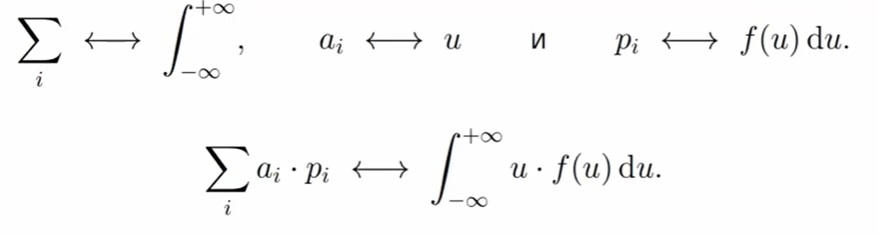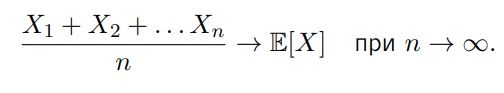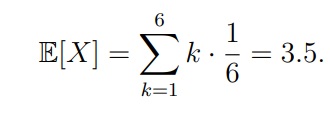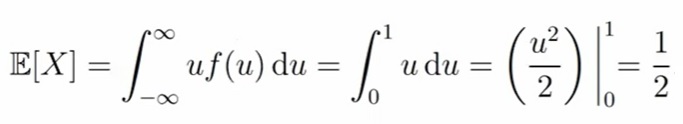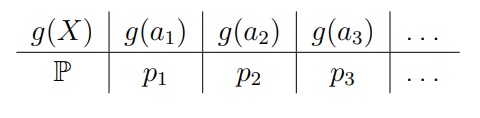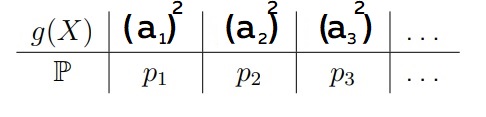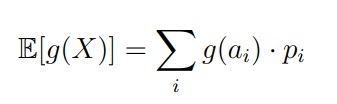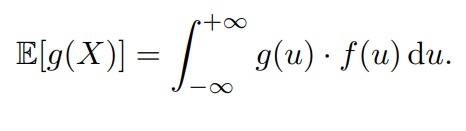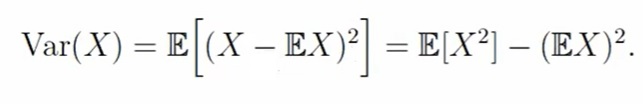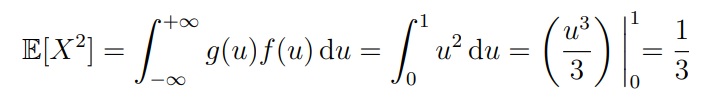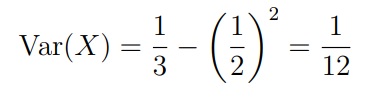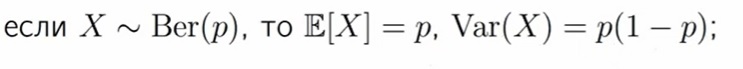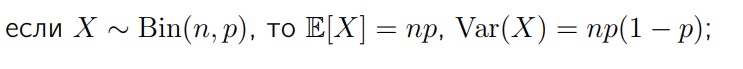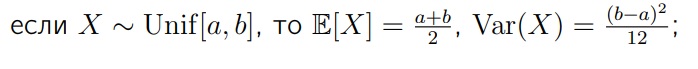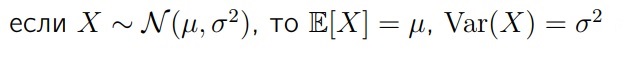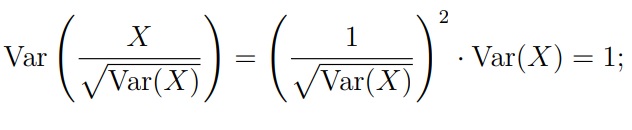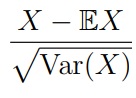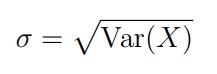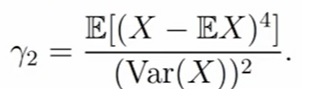Числовые характеристики распределения вероятностей. Математическое ожидание, дисперсия и стандартное отклонение
- Закон распределения дискретной случайной величины
- Математическое ожидание
- Дисперсия
- Среднее квадратичное отклонение
- Правило трёх сигм
- Примеры
п.1. Закон распределения дискретной случайной величины
Законом распределения дискретной случайной величины называют соответствие между полученными на опыте значениями этой величины X= {xi} и их вероятностями pi = P(xi).
При этом сумма всех вероятностей равна 1: (mathrm{sum_{i=1}^n p_i=1})
Закон распределения можно задать таблицей, графиком или аналитически (в виде формулы).
Например:
Закон распределения случайной величины X = {0;1;2;3}, равной числу выпадения орлов при 3 бросках монеты, аналитически задаётся формулой: $$ mathrm{ p_i=P(x_i)=P_3(i)=frac{C_3^{i}}{2^3}, i={0;1;2;3} } $$
В табличном виде:
|
xi |
pi |
|
0 |
1/8 |
|
1 |
3/8 |
|
2 |
3/8 |
|
3 |
1/8 |
В виде графика:
п.2. Математическое ожидание
Математическое ожидание дискретной случайной величины X = {xi} равно сумме произведений всех возможных значений xi на соответствующие вероятности pi: $$ mathrm{ M(X)=x_1p_1+x_2p_2+…+x_{n}p_{n}=sum_{i=1}^n x_{i}p_{i} } $$ Математическое ожидание является средним значением величины X.
Свойства математического ожидания
1) Размерность математического ожидания равна размерности случайной величины.
2) Математическое ожидание может быть любым действительным числом: положительным, равным 0, отрицательным.
3) Математическое ожидание постоянной величины равно этой постоянной:
M(C) = C
4) Математическое ожидание суммы независимых случайных величин равно сумме математических ожиданий:
M(X + Y) = M(X) + M(Y)
5) Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий:
M(XY) = M(X) · M(Y)
6) Постоянный множитель можно вынести за знак математического ожидания:
M(CX) = C · M(X)
Например:
Пусть в результате экспериментов получено следующее распределение случайной величины X – числа появления белых шаров (см. пример 1, §40 данного справочника):
| Число белых шаров, xi | 0 | 1 | 2 | 3 | 4 | 5 |
| pi | (mathrm{C_5^0q^5}) | (mathrm{C_5^1pq^4}) | (mathrm{C_5^2p^2q^3}) | (mathrm{C_5^3p^3q^2}) | (mathrm{C_5^4p^4q}) | (mathrm{C_5^5p^5}) |
| 0,0074 | 0,0618 | 0,2060 | 0,3433 | 0,2861 | 0,0954 |
Найдём математическое ожидание для данного распределения:
M(X) = 0 · 0,0074 + 1 · 0,0618 + … + 5 · 0,0954 = 3,125
п.3. Дисперсия
Дисперсия дискретной случайной величины X = {xi} – это математическое ожидание квадрата отклонения случайной величины от её математического ожидания: $$ mathrm{ D(X)=M(X-M(X))^2 } $$ На практике дисперсия рассчитывается по формуле: $$ mathrm{ D(X)=M(X)^2-M^2(X)=sum_{i=1}^n x_i^2p_i-M^2(X) } $$
Свойства дисперсии
1) Размерность дисперсии равна квадрату размерности случайной величины.
2) Дисперсия может быть любым неотрицательным действительным числом.
3) Дисперсия постоянной величины равна нулю:
D(C) = 0
4) Дисперсия суммы независимых случайных величин равна сумме дисперсий:
D(X + Y) = D(X) + D(Y)
5) Постоянный множитель можно вынести за знак дисперсии:
D(CX) = C2 · D(X)
Например:
Продолжим исследование и найдём дисперсию для распределения случайной величины X – числа появления белых шаров. Составим расчётную таблицу:
pi
0,0074
0,0618
0,2060
0,3433
0,2861
0,0954
1
xip1
0
0,0618
0,4120
1,0300
1,1444
0,4768
3,125
(mathrm{x_i^2})
0
1
4
9
16
25
–
(mathrm{x_i^2p_i})
0
0,0618
0,8240
3,0899
4,5776
2,3842
10,9375
Получаем: D(X) = 10,9375 – 3,1252 ≈ 1,1719.
п.4. Среднее квадратичное отклонение
Среднее квадратичное отклонение (СКО) дискретной случайной величины X = {xi} – это корень квадратный от дисперсии: $$ mathrm{ sigma(X)=sqrt{D(X)} } $$ СКО характеризует степень отклонения случайной величины от среднего значения.
Свойства СКО
1) Размерность СКО равна размерности случайной величины.
2) СКО может быть любым неотрицательным действительным числом.
3) СКО постоянной величины равно нулю:
σ(C) = 0
4) Постоянный множитель можно вынести за знак СКО:
σ(CX) = C · σ(X)
п.5. Правило трёх сигм
Большое количество случайных величин, измеряемых в экспериментах (например, в школьных лабораторных работах), имеет так называемое нормальное распределение.
В частности, при больших n, биномиальное распределение можно с хорошей точностью описывать как нормальное с M(X) = np и (mathrm{sigma(X)=sqrt{npq}}).
График плотности нормального распределения p(x) похож на колокол, с максимумом, соответствующим M(X) = Xcp – среднему значению измеряемой величины.
Величина СКО σ(X) характеризует степень отклонения X от среднего значения M(X).
Если величина X имеет нормальное распределение, то в пределах
±σ лежит 68,26% значений, принимаемых этой величиной
±2σ лежит 95,44% значений, принимаемых этой величиной
±3σ лежит 99,72% значений, принимаемых этой величиной
Вероятность того, что нормально распределённая величина примет значение, отклоняющееся от среднего больше, чем на «три сигмы», равна 0,28%, т.е. пренебрежимо мала.
п.6. Примеры
Пример 1. Найдите математическое ожидание, дисперсию и СКО при бросании кубика.
Закон распределения величины X – очки на верхней грани при бросании кубика и расчётная таблица:
pi
1/6
1/6
1/6
1/6
1/6
1/6
1
xip1
1/6
1/3
1/2
2/3
5/6
1
3,5
(mathrm{x_i^2})
1
4
9
16
25
36
–
(mathrm{x_i^2p_i})
(mathrm{frac16})
(mathrm{frac23})
(mathrm{1frac12})
(mathrm{2frac23})
(mathrm{4frac16})
6
(mathrm{15frac16})
Получаем: begin{gather*} mathrm{ M(X)=sum_{i=1}^6 x_ip_i=3,5 }\ mathrm{ D(X)=sum_{i=1}^6 x_i^2p_i-M^2(X)=15frac16-3,5^3=2frac{11}{12} }\ mathrm{ sigma(X)=sqrt{D(X)}=sqrt{2frac{11}{12}}approx 1,7 } end{gather*} Ответ: (mathrm{M(X)=3,5; D(X)=2frac{11}{12}; sigma(X)approx 1,7}).
Пример 2*. Найти математическое ожидание, дисперсию и СКО суммы очков при бросании двух кубиков.
Используем свойства мат.ожиданий и дисперсий.
Пусть X – очки на первом кубике, Y – на втором.
Параметры распределения для каждого из кубиков рассчитаны в примере 1.
(mathrm{M(X)=M(Y)=3,5, D(X)=D(Y)=2frac{11}{12}}).
Для суммы очков получаем:
(mathrm{M(X+Y)=M(X)+M(Y)=3,5+3,5=7})
(mathrm{D(X+Y)=D(X)+D(Y)=2frac{11}{12}+2frac{11}{12}=5frac56})
(mathrm{sigma(X+Y)=sqrt{D(X+Y)}=sqrt{5frac56}approx 2,4})
Ответ: (mathrm{M(X+Y)=7; D(X+Y)=5frac56; sigma(X+Y)approx 2,4}).
Пример 3*. Докажите, что в опытах по схеме Бернулли математическое ожидание M(X)=np, а дисперсия D(X)=npq.
Проведем один опыт. В нём может быть только два исхода: «успех» и «неудача».
Составим расчётную таблицу:
(mathrm{x_i^2p_i})
0
p
p
Мат.ожидание первого опыта (mathrm{M(X)=sum x_ip_i=p}).
Общее число успехов при n опытах складывается из числа успехов при каждом опыте, т.е. (mathrm{X=X_1+X_2+…+X_n}). Все опыты между собой независимы.
По свойству мат.ожидания суммы независимых событий: begin{gather*} mathrm{ M(X)=M(X_1+X_2+…+X_n)=M(X_1)+M(X_2)+…+M(X_n)= }\ mathrm{=underbrace{p+p+…+p}_{n text{раз}}=np } end{gather*} Дисперсия первого опыта (mathrm{D(X)=sum x_i^2p_i-M(X)=p-p^2=p(1-p)=pq})
По свойству дисперсии суммы независимых событий: begin{gather*} mathrm{ D(X)=D(X_1+X_2+…+X_n)=D(X_1)+D(X_2)+…+D(X_n)= }\ mathrm{=underbrace{pq+pq+…+pq}_{n text{раз}}=npq } end{gather*} Что и требовалось доказать.
Пример 4. 100 канцелярских кнопок высыпали на стул. Вероятность, что кнопка упала острием вверх, равна 0,4. Найдите среднее количество, дисперсию и СКО для числа кнопок, упавших острием вверх. Найдите интервал оценки для количества этих кнопок по правилу «трёх сигм».
По условию n = 100, p = 0,4.
Для каждой кнопки может быть два исхода: упасть острием вверх или вниз.
Таким образом, это испытание Бернулли с биномиальным распределением случайной величины. begin{gather*} mathrm{ M(X)=np=100cdot 0,4=40 }\ mathrm{D(X)=npq=100cdot 0,4cdot 0,6=24 }\ mathrm{sigma(X)=sqrt{D(X)}=sqrt{24}approx 4,9} end{gather*} Интервал оценки «три сигмы»: begin{gather*} mathrm{ M(X)-3sigma(X)lt Xlt M(X)+3sigma(X) }\ mathrm{40-3cdot 4,9lt Xlt 40+3cdot 4,9 }\ mathrm{25,3lt Xlt 54,7}\ mathrm{26leq Xleq 54} end{gather*} Скорее всего (99,7%), от 26 до 54 кнопок будут острием вверх.
Ответ: (mathrm{M(X)=40; D(X)=24; sigma(X)approx 4,9; 26leq Xleq 54})
Пример 5*. В тесте 10 задач с 4 вариантами ответов. Ответы выбираются наугад. Постройте распределение величины X = «количество угаданных ответов», найдите числовые характеристики этого распределения.
Найдите интервал оценки для количества угаданных ответов по правилу «трёх сигм».
Какова вероятность угадать хотя бы 1 ответ? Хотя бы 5 ответов? Угадать все 10 ответов?
По условию: (mathrm{n=10, p=frac14, q=frac34}).
Для каждого ответа может быть два исхода: «угадал»/ «не угадал».
Таким образом, это испытание Бернулли с биномиальным распределением случайной величины. $$ mathrm{ P_{10}(k)=C_{10}^kp^kq^{10-k}=C_{10}^kfrac{3^{10-k}}{4^{10}}=left(frac34right)^{10}frac{C_{10}^k}{3^k} } $$ Строим расчётную таблицу. Для (mathrm{C_{10}^k}) используем рекуррентную формулу (см. §36 данного справочника): $$ mathrm{ C_{n}^k=frac{n-k+1}{k}C_n^{k-1} } $$
| (mathrm{x_i=k}) | (mathrm{C_k}) | (mathrm{3^k}) | (mathrm{p_i(x_i)}) | (mathrm{x_icdot p_i}) | (mathrm{x_i^2}) | (mathrm{x_i^2cdot p_i}) |
| 0 | 1 | 1 | 0,0563135 | 0,0000000 | 0 | 0,0000000 |
| 1 | 10 | 3 | 0,1877117 | 0,1877117 | 1 | 0,1877117 |
| 2 | 45 | 9 | 0,2815676 | 0,5631351 | 4 | 1,1262703 |
| 3 | 120 | 27 | 0,2502823 | 0,7508469 | 9 | 2,2525406 |
| 4 | 210 | 81 | 0,1459980 | 0,5839920 | 16 | 2,3359680 |
| 5 | 252 | 243 | 0,0583992 | 0,2919960 | 25 | 1,4599800 |
| 6 | 210 | 729 | 0,0162220 | 0,0973320 | 36 | 0,5839920 |
| 7 | 120 | 2187 | 0,0030899 | 0,0216293 | 49 | 0,1514053 |
| 8 | 45 | 6561 | 0,0003862 | 0,0030899 | 64 | 0,0247192 |
| 9 | 10 | 19683 | 0,0000286 | 0,0002575 | 81 | 0,0023174 |
| 10 | 1 | 59049 | 0,0000010 | 0,0000095 | 100 | 0,0000954 |
| Σ | 1 | 2,5 | 8,125 |
Получаем: begin{gather*} mathrm{ M(X)=sum_{i=0}^{10} x_ip_i=2,5 }\ mathrm{ D(X)=sum_{i=0}^{10} x_i^2p_i-M^2(X)=8,125=2,5^2=1,875 }\ mathrm{ sigma(X)=sqrt{D(X)}=sqrt{1,875}approx 1,37 } end{gather*}
Интервал оценки «три сигмы»: begin{gather*} mathrm{ M(X)-3sigma(X) lt Xlt M(X)+3sigma(X) }\ mathrm{ 2,5-3cdot 1,37lt X lt 2,5+3cdot 1,37 }\ mathrm{ -1,61lt Xlt 6,61 }\ mathrm{ 0leq Xleq 6 } end{gather*} Скорее всего (по расчетам – 99,65%), вы угадаете от 0 до 6 ответов.
Вероятность угадать хотя бы один ответ: begin{gather*} mathrm{ P(Xgeq 1)=1-p_0approx 1-0,0563=0,9437 }end{gather*} Очень хорошие шансы – 94,37%.
Вероятность угадать хотя бы 5 ответов: begin{gather*} mathrm{ P(Xgeq 5)=1-left(sum_{i=0}^{4}{p_i} right)approx 1-(0,0563+0,1877+…+0,1460)=0,0781 }end{gather*} Шансов мало – 7,81%. Т.е. «средний балл» при сдаче тестов мало достижим методом научного тыка.
Вероятность угадать все 10 ответов: p10≈ 0,000001. Шанс – один из миллиона.
Решение типовых примеров:
Пример
1. Найти
математическое ожидание, дисперсию и
среднее квадратическое отклонение
случайной величины Х, имеющей следующий
закон распределения:
|
Х |
1 |
2 |
3 |
4 |
5 |
|
Р |
0,1 |
0,2 |
0,3 |
0,3 |
0,1 |
Решение:
Находим
математическое ожидание случайной
величины Х и ее квадрата:
Отсюда,
по формуле дисперсии находим:
Среднее
квадратическое отклонение случайной
величины Х равно:
.
Ответ:
.
Пример
2. Математическое
ожидание и дисперсия случайной величины
Х равны:
Найти
математическое ожидание и дисперсию
величины
Решение:
Согласно
свойствам 1-3 математического ожидания,
мы имеем:
Согласно
свойствам 1-3 дисперсии:
Ответ:
Задания для закрепления:
1.
Строительная инвестиционная компания
в настоящий момент продает акции по 16
условных денежных единиц за штуку.
Инвестор планирует покупку пакета акций
и предполагает хранение их в течении
года. Пусть Х — случайная величина,
означающая цену одной акции спустя год.
Ряд распределения Х задан в таблице:
-
цена
акции — ХР(Х)
16
17
18
19
20
0,35
0,25
0,25
0,10
0,05
а)
Показать, что заданное распределение
обладает всеми свойствами ряда
распределения.
б)
Чему равно ожидаемое среднее значение
цены акции спустя один год?
в)
Чему равен ожидаемый средний выигрыш
от акции спустя год? Чему равен процент
возврата инвестиций, отражаемый этим
ожидаемым значением?
г)
Определите дисперсию цены акции спустя
год.
Ответ:
б) 17,25; в) 1,25; г) 1,3875.
2.
Два строительных контракта случайным
образом распределяются среди трех фирм:
I,
II,
III.
Любая фирма может получить или один или
оба контракта. С каждого полученного
контракта прибыль фирмы составит 90000
условных денежных единиц.
а)
Найдите ожидаемую прибыль фирмы I.
б)
Если фирмы I
и II
принадлежат одному владельцу, то какова
ожидаемая общая прибыль владельца?
Ответ:
М(средняя прибыль)=60000; М(общая прибыль)=
120000.
3.
Некоторое предприятие планирует
реконструкцию и расширение производства
для выпуска новой продукции. Руководство
предприятия должно определить стратегию
реконструкции и выбрать один из двух
проектов, предусматривающих большие и
умеренные капиталовложения. Неопределенность
заключается в том, что спрос на новою
продукцию, которую собирается выпускать
предприятие неизвестен. Будущий спрос
может быть низким, умеренным и высоким.
Вероятности оцениваются как 0,20, 0,50 и
0,30 соответственно. Пусть Х означает
ежегодный доход 1000 условных денежных
единиц. Предприятие планирует следующий
доход для проектов с большими и умеренными
капиталовложениями:
|
доход
значительных |
доход
умеренных |
|||
|
спрос |
Х |
Р(Х) |
Х |
Р(Х) |
|
низкий умеренный высокий |
0 100 300 |
0,20 0,50 0,30 |
50 150 200 |
0,20 0,50 0,30 |
а)
вычислите
ожидаемое среднее значение дохода при
двух альтернативных типах реконструкции
предприятия. Какое решение предпочтительнее
для максимизации ожидаемого дохода?
б)
вычислите
дисперсию дохода для двух альтернативных
проектов. Какое решение Вы предпочтете
для минимизации риска и неопределенности?
Ответ:
а) М(Х) = 145; 140; б) D(Х)
= 2725; 12400.
4.
Доход от некоторого рискованного бизнеса
составляет сумму около 1000 условных
денежных единиц с заданным рядом
распределения:
|
xi |
-2000 |
-1000 |
0 |
1000 |
2000 |
3000 |
|
P(X=xi)=pi |
0,1 |
0,1 |
0,2 |
0,2 |
0,3 |
0,1 |
Замечание:
-2000, -1000 означают убыток.
а)
какой
наиболее вероятностный денежный доход
рискованного бизнеса?
б)
является
ли этот риск вероятностно успешным?
Объясните.
в)
чему равен на длительный период средний
доход от этого бизнеса?
Ответ:
в) 800.
5.
Найти математическое ожидание, дисперсию,
стандартное отклонение случайной
величины Х для условия задачи 7 предыдущего
параграфа.
Ответ:
6.
Для закона распределения задачи 5
предыдущего параграфа определить
ожидаемую среднюю сумму штрафа, если
предположить, что штраф, предъявляемый
машинистке за ошибки, исчисляется как
корень квадратный из числа ошибок на
страницу,
и каждая единица приравнивается к 1
условной денежной единице.
Ответ:
1,73 усл. ден. ед.
7.
Исходя из закона распределения ежедневных
продаж автомобилей, соответствующего
данным,
условия задачи 8 предыдущего параграфа,
определить ожидаемую среднюю сумму
заработка продавца, если предположить,
что он зарабатывает сумму, которая
рассчитывается как корень квадратный
из числа проданных автомобилей, умноженный
на 300 условных денежных единиц.
Ответ:
465,85797 усл. ден. ед.
8.
Чему равен ожидаемый процент людей,
откликнувшихся
на рекламу, если ряд распределения такой
же,
как и в задаче 6 из предыдущего параграфа?
Чему равны дисперсия и среднее
квадратическое отклонение?
Ответ:
9.
По данным условия задачи 4 предыдущего
параграфа определить чему равна
вероятность того, что в какой-то
определенный день число прибывающих
судов превысит ожидаемое среднее.
Ответ:
0,3.
-
Найти
математическое ожидание дискретной
случайной величины Х, заданной законом
распределения :
Х
0,21 0,54 0,61
р 0,1 0,5 0,4
Ответ:
MХ=0,535.
11.
Найти математическое ожидание случайной
величины Z=3Х+4Y,
если известно, что МХ=2 и МY=6.
Ответ: MZ=30.
12.
Случайные величины X
и Y
независимы. Найти дисперсию случайной
величины Z=2Х+3Y,
если известно, что DХ=4
и DY=5.
Ответ:
DZ=61.
13.
Дан перечень возможных значений
дискретной случайной величины Х: ,
а
так же даны математическое ожидание
этой величины и ее квадрата: МХ=2,3
и МХ2=5,9.
Найти вероятности, соответствующие
возможным значениям Х.
Ответ:
.
14.
Дискретная случайная величина Х имеет
только три значения:
,
причем
.
Вероятности того, что Х примет значения
х1
и х2
, соответственно равны 0,3 и 0,2. Найти
закон распределения величины Х, зная
ее математическое ожидание МХ=2,2 и
дисперсию DХ=
0,76.
Ответ:
Х 1 2 3
р
0,3 0,2 0,5.
15.
Брошены n
игральных костей. Найти дисперсию суммы
числа очков, которые могут появится на
всех выпавших гранях.
Ответ:
DХ=35n/12.
16.
Отдел технического контроля проверяет
изделия на стандартность. Вероятность
того, что изделие стандартно, равна 0,9.
В каждой партии содержится 5 изделий.
Найти математическое ожидание дискретной
случайной величины Х — числа партий, в
каждой из которых окажется ровно 4
стандартных изделия; если проверке
подлежит 50 партий.
Ответ:
.
-
Бросают
n
игральных костей. Найти математическое
ожидание числа таких бросаний, в каждом
из которых выпадет ровно m
шестерок, если общее число бросаний
равно N.
Ответ:
.
9-Занятие.
Моменты
высокого порядка. Коэффициент корреляции
и свойства
Начальный
момент порядка k
непрерывной
случайной величины Х, возможные значения
которой принадлежат всей оси ОХ,
определяется равенством: .
Центральный
момент порядка k
непрерывной
случайной величины Х, возможные значения
которой принадлежат всей оси ОХ,
определяется равенством:
.
Очевидно,
что если k=1,
то
.
Центральные
моменты выражаются через начальные
моменты по следующим формулам:
Как найти математическое ожидание?
Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание — это первый начальный момент заданной СВ.
Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины — срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).
Нужна помощь? Решаем теорию вероятностей на отлично
Спасибо за ваши закладки и рекомендации
Формула среднего случайной величины
Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Пример нахождения математического ожидания
Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.
Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Используем формулу для м.о. дискретной случайной величины:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Получаем:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Вот в этом примере 2 описано также нахождение дисперсии Х.
Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.
Используем для нахождения мат. ожидания формулу:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Подставляем из условия плотность вероятности и вычисляем значение интеграла:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{1} 12(x^2-x^3) cdot x dx = int_{0}^{1} 12(x^3-x^4) dx = \
=left.(3x^4-frac{12}{5}x^5) right|_0^1=3-frac{12}{5} = frac{3}{5}=0.6.
$$
Другие задачи с решениями по ТВ
Подробно решим ваши задачи по теории вероятностей
Вычисление математического ожидания онлайн
Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку «Вычислить».
- Калькулятор покажет вычисленное математическое ожидание $M(X)$.
Видео. Полезные ссылки
Видеоролики: что такое среднее (математическое ожидание)
Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Лучшее спасибо — порекомендовать эту страницу
Полезные ссылки
А теперь узнайте о том, как находить дисперсию или проверьте онлайн-калькулятор для вычисления математического ожидания, дисперсии и среднего квадратического отклонения дискретной случайной величины.
Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по терверу. Для закрепления материала — еще примеры решений по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Содержание:
Числовые характеристики случайных величин:
Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.
Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.
Математическое ожидание случайной величины
Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся
Рассмотрим свойства математического ожидания.
- Математическое ожидание постоянной величины равно самой постоянной: М(С) = С. (5.3)
- Постоянный множитель можно выносить за знак математического ожидания, т.е. M(СX) = С·M(X). (5.4)
- Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е
- Математическое ожидание произведений конечного числа случайных величин равно произведению их математических ожиданий, т.е. M(XY) = M(X)·M(Y). (5.6)
- Если все значения случайной величины увеличить (или уменьшить) на постоянную С, то на эту же постоянную С увеличится (или уменьшится) математическое ожидание этой случайной величины:
- Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
Пример:
Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение:
Используя свойства 1, 2, 3 математического ожидания, находим
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дисперсия случайной величины
Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
Для дискретной случайной величины X эта формула принимает вид:
Для непрерывной случайной величины: 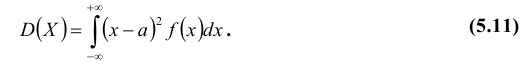
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: 

Рассмотрим свойства дисперсии.
- Дисперсия постоянной величины равна нулю:
- Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.
- Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.
- Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.
Пример №1
Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.
Решение:
Используя свойства дисперсии, находим
Среднее квадратическое отклонение случайной величины
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии:
Свойства среднего квадратического отклонения вытекают из свойств дисперсии.
Мода и медиана. Квантили
Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.
Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.
Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого 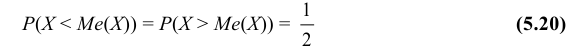
Пример №2
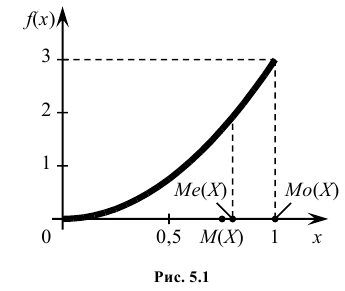
Найти моду, медиану случайной величины Х с плотностью вероятности
Решение:
Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия 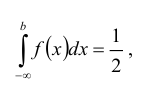
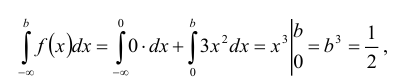
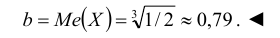
Наряду с модой и медианой для описания случайной величины используется понятие квантиля.
Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.
Пример №3
По данным примера 5.3 найти квантиль
Решение:
Находим функцию распределения 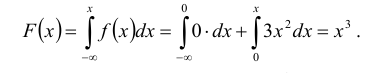
Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.
Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины: 

Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания:
Для дискретной случайной величины формула центрального момента имеет вид:
Для непрерывной случайной величины: 
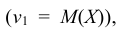
Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.
Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на 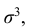
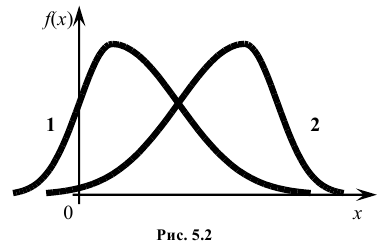
Полученная величина А называется коэффициентом асимметрии случайной величины: 
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0).
Четвертый центральный момент μ4 служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом случайной величины называется число 
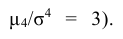
Числовые характеристики независимых испытаний
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (т.е. повторные независимые испытания). В этом случае математическое ожидание числа появлений события А в n испытаниях находится по формуле M(X) = np, (5.30) а дисперсия по формуле D(X) = npq. (5.31)
Одинаково распределенные взаимно независимые случайные величины
Рассмотрим n взаимно независимых случайных величин 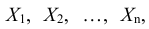
Обозначим среднее арифметическое n взаимно независимых случайных величин через
Сформулируем положения, устанавливающие связь между числовыми характеристиками среднего арифметического 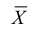
- Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
- Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в
раз меньше дисперсии D каждой из величин:
- Среднее квадратическое отклонение n одинаково распределенных взаимно независимых случайных величин в n раз меньше среднего квадратического отклонения σ каждой из величин:
Пример:
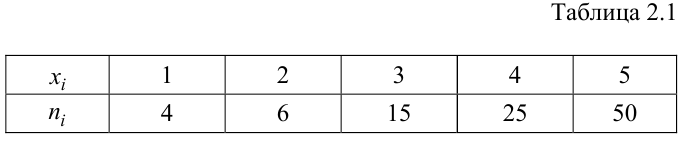
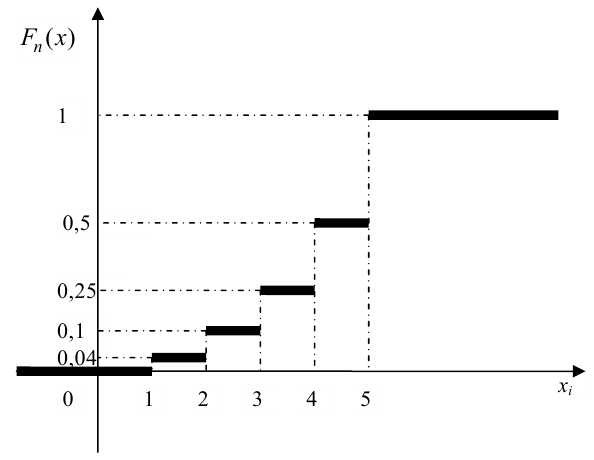
По данному распределению выборки (табл. 2.1) найти эмпирическую функцию распределения.
Решение. Определяем объем выборки:
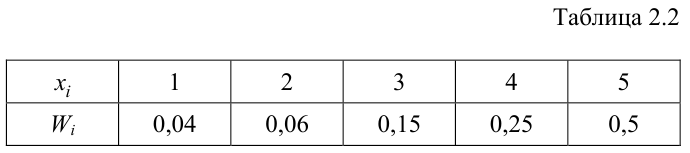
Определяем относительные частоты вариант (табл. 2.2):
Так как значение 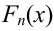
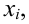
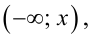
График примет вид:
- Нормальный закон распределения
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
Математикам прошлого не сиделось на месте, дай волю, как они опять что-нибудь придумают и накатают очередной, наскоро состряпанный, фундаментальный манифест. А нам потом разгребать. Сегодня это будет математическое ожидание. Как гласит вики, это одно из важнейших понятий в теории вероятностей, означающее среднее (взвешенное по вероятностям возможных значений) значение случайной величины
Математическое ожидание
Для дискретной случайной величины X с таблицей распределения
Математическим ожиданием (или средним значением) называется число E[X], которое вычисляется по формуле
Для непрерывный случайной величины X с плотностью f(u) математическим ожиданием (или средним значением) называется число E[X], которое вычисляется по формуле
Математическое ожидание тоже подходит для правила перехода из дискретного случая в непрерывному. Сумму меняем на интеграл, ai меняем на аргумент функции плотности, Pi меняем на f(u)du. Формула следующая:
Как интерпретировать математическое ожидание?
Математическое ожидание это, в некотором смысле, среднее значение случайной величины. Окей, мы перемножили значения на вероятности из таблички. Мы получили какое-то число. Допустим, пять. Что оно значит?
Физический смысл: если на отрезке, распределить единичную массу согласно распределению (в дискретном случае поместив в точки ai массу pi , а в непрерывном — согласно плотности f), то точка E[X] будет координатой «центра масс» отрезка.
Вероятностный смысл: при многократном повторении эксперимента, ассоциированного с X, среднее арифметическое получившихся значений X1, X2, X3, . . . будет стремиться к E[X], т.е. эксперимент мы повторяем бесконечное количество раз и записываем результат (X1, X2, X3…Xn). Если мы посчитаем среднее арифметическое результата n-экспериментов, то это число и будет математическим ожиданием случайной величины, при n стремящемуся к бесконечности
Этот факт называется «Законом больших чисел»
Давайте решим задачку.
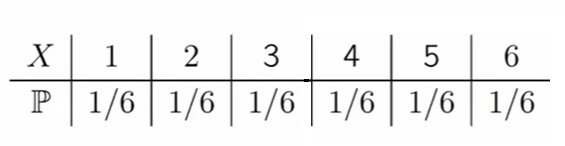
Пусть случайная величина X равна числу очков, выпадающих при одном подбрасывании игральной кости. Найти математическое ожидание E[X]
Как мы помним, вероятность выпадения каждой стороны кубика у нас 1/6
Как мы помним по формуле в начале статьи, нам нужна сумма всех возможных значений случайной величины перемноженных на вероятность их наступления (ai x pi):
E[X] = 1*1/6, 2*1/6, 3*1/6, 4*1/6, 5*1/6, 6*1/6 = 21/6 = 3,5
По науке формула будет выглядеть так:
Давайте найдем математическое ожидание (E[X]) равномерного распределения на отрезке от 0 до 1 (Unif[0, 1]). Тут даже без решения понятно, что «центр массы» у нас будет ровно посередине отрезка. С формулой это выглядит так:
Свойства математического ожидания:
- E[c] = c для любого c ∈ R (математическое ожидание для константы будет равно константе)
- E[cX] = cE[X] для любого c ∈ R (константу можно выносить из мат. ожидания)
- E[X + Y ] = E[X] + E[Y] для любых X и Y (мат. ожидание суммы это всегда сумма мат. ожиданий)
- E[X · Y ] = E[X] · E[Y], если X и Y независимы (мат. ожидание произведений — это произведение мат. ожиданий, если случайные величины независимы)
- Если X ≥ 0, то E[X] ≥ 0 (если случайная величина у нас не отрицательна, соотв. мат. ожидание тоже не отрицательно)
Преобразование случайной величины
Очень часто другие характеристики случайных величин тоже вычисляются как математическое ожидание (не обычное, а от некоторого преобразования случайной величины X). Для этого мы будем использовать произвольную функцию g, т.е. в итоге нам нужно будет найти E[g(X)].
В дискретном случае распределение g(X) будет следующим:
Как это будет выглядеть: если у нас математическое ожидание принимает вид E[x2], то случайная величина X примет значение (а1)2 . Заметим, что вероятность (p) остаётся точно такой же
Формула для дискретного распределения:
Формула для непрерывного распределения:
Дисперсия
Если математическое ожидание характеризует среднее значение случайной величины, дисперсия, наоборот, показывает разброс значения случайной величины относительно её математического ожидания. Дисперсия обозначается, как Var(X) и вычисляется по формуле ниже, т.е. дисперсия — это математическое ожидание от формулы случайная величина минус математическое ожидание X в квадрате:
Второй вариант формулы (после второго равно) получается, если применить свойство мат. ожидания. По первому варианту формулы удобней интерпретировать понятие дисперсии. По второму варианту — считать
Стоит заметить, что определение для дискретных и непрерывных распределений — оно одинаковое, однако, мат. ожидание будет считаться в этих случаях по-разному
Как интерпретировать математическое ожидание?
Дисперсия характеризует степень разброса значений случайной величины вокруг её мат. ожидания
Задача
Задача 1. Пусть случайная величина имеет равномерное распределение X ∼ Unif[0, 1]. Найти дисперсию Var(X).
Для решения будем использовать формулу Var(X) = E[X2] − (EX)2
Чтобы найти E[X2], заметим, что это E[g(X)] для g(u) = u2 . Из этого следует, что:
Если E[X] = 1/2, мы получим
Свойства дисперсии
- Var(c) = 0 для любого c ∈ R (дисперсия константы равна нулю)
- Var(cX) = c2 Var(X) для любого c ∈ R (константа тоже выносится с квадратом
- Var(X + Y ) = Var(X) + Var(Y ), если X и Y независимы (дисперсия суммы —
- это сумма дисперсий для независимых случайных величин)
- Var(X + c) = Var(X) для любого c ∈ R (Если мы к случайной величине добавляем константу, то дисперсия никак не учитывает, т.к. это не влияет на сам разброс)
- Var(X) ≥ 0 (дисперсия не может быть отрицательной)
Итого:
Математическое ожидание и дисперсия являются «базовыми» числовыми характеристиками распределений.
Дисперсия для распределение Бернулли: вероятность успеха умноженная на вероятность неуспеха
Дисперсия для биномиального распределения: Все характеристики умножаются на n
Дисперсия для равномерного распределения:
Дисперсия для нормального распределения: Сигма в квадрате
Базовые операции для случайных величин
Центрирование: вычитание из X ее мат. ожидания EX. Это операция позволяет сделать так, чтобы у случайной величины было мат. ожидание, которое равно нулю
E[X − EX] = E[X] − E[X] = 0
Нормирование: деление X на p Var(X). Дисперсию приводим к единице.
Стандартизация: центрирование + нормирование
Среднеквадратическое отклонение (или стандартное отклонение) — это квадратный корень из дисперсии случайной величины:
Разделив случайную величину X на σ, мы получим случайную величину с дисперсией Var(X/σ) = 1. Эта операция называется нормировкой.
Характеристики среднего значения случайной величины
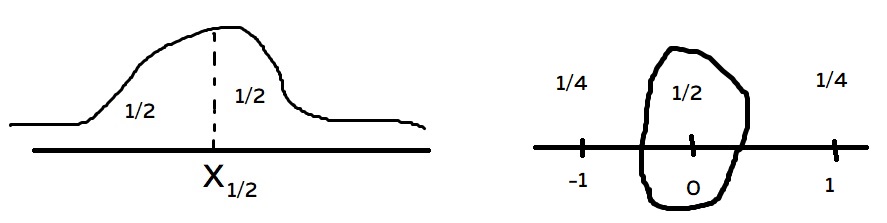
Теоретическая медиана случайной величины X — это число x1/2, удовлетворяющее неравенствам
Медиана — некоторая точка x1/2, которая делит функцию плотности пополам с точки зрения площади под графиком
Теоретическая мода:
• В дискретном случае — значение, которое принимаются с наибольшей вероятностью.
• В непрерывном случае — точка максимума функции плотности
Моменты старших порядков
• E[Xk] — k-ый момент (или момент порядка k)
• E[|X|k] — абсолютный k-ый момент X
• E[(X − EX)k] — центральный k-ый момент X
• E[|X − EX|k] — абсолютный центральный k-ый момент X
Все вышеприведенные моменты характеризуют распределение случайной величины. Они часто появляются в задачах концентрации
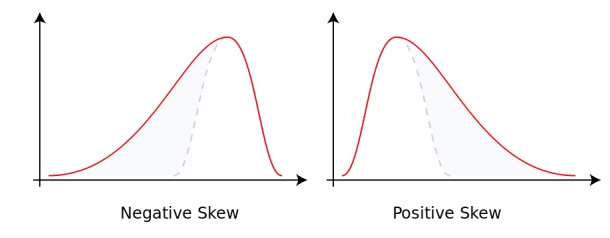
Коэффициент асимметрии (Skewness). Коэффициент асимметрии — величина, характеризующая асимметрию распределения данной случайной величины. Он показывает, если ли у нас скошенность в какую-либо сторону.
Например, вы работаете с выборкой и хотите проверить является ли она «нормальной» — там могут быть ошибки, но если они распределены нормально, то теоретические свойства модели будут хорошими. Чтобы проверить выборку можно использовать коэффициент асимметрии.
Если значение γ1 по модулю большое, то в выборке есть скошенность. Если значение близко к нулю, то ваша выборка нормальная.
γ1 — нормированный центральный момент порядка 3
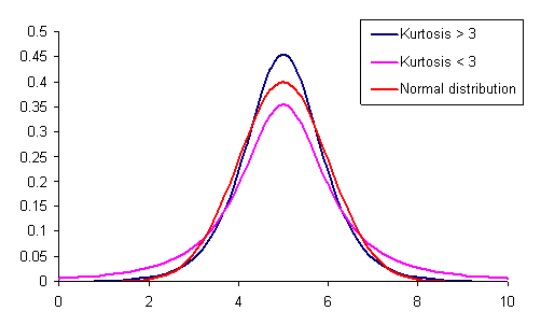
Коэффициент эксцесса (Kurtosis) — величина, которая характеризуют кривизну функции плотности около точки максимума. По научному — это мера остроты пика плотности
распределения случайной величины.
γ2 — нормированный центральный момент порядка 4. Если мы получим коэффициент эксцесса больше трёх, то это означает, что около точки максимума функция плотность имеет более острый пик, если меньше — функция плотности имеет меньшую кривизну





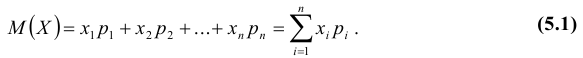
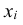
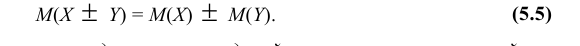


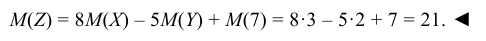







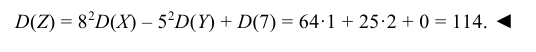
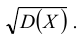

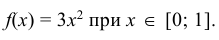

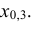
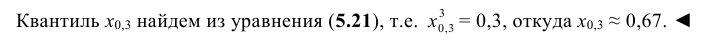



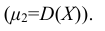
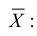
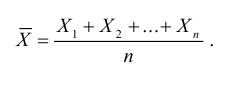

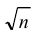 раз меньше дисперсии D каждой из величин:
раз меньше дисперсии D каждой из величин: