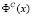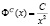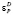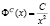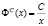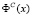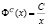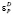Модели спроса и
потребления являются инструментарием,
предназначенным для анализа и
прогнозирования процессов формирования
спроса и потребления населения. Модели
позволяют характеризовать зависимость
объема и структуры личного потребления
и спроса населения от доходов, цен и
социально-демографических факторов.
Наибольшее распространение получила
модель оптимизации потребительского
поведения с ограничениями бюджетного
типа:
,
,
где
— целевая функция потребления,
характеризующая предпочтение потребителя,,
— количество рассматриваемых благ,
— объем потребления блага
,
— доход (бюджет) потребителя,
— цена единицы блага
.
Модель может описывать, как поведение
индивидуального потребителя, так и
предпочтения однородной группы
потребителей. В последнем случае
предполагается, что все входящие в
группу потребители приобретают товары
по одним и тем же ценам,
— вектор среднедушевого потребления
группы,— среднедушевой доход. Модель прогнозирует
реальное поведение, исходя из предположения
о том, что оно направлено на оптимизацию
потребительских предпочтений при
заданных ограничениях.
Проводя расчеты
при разных значениях
и
,
получают систему функций спроса,
связывающих объем потребления благас ценами и доходами:
,
что графически
может быть представлено в виде кривых
безразличия.
Зависимость
потребительского спроса на благо
от дохода и цен характеризует безразмерные
величины эластичности спроса по доходу
и ценам. Эластичность спроса по доходу
показывает на сколько процентов изменится
спрос на данное благо при изменении
дохода потребителя на 1%. Для благаэтот параметр определяется формулой
.
Более высокие
значения эластичностей свидетельствуют
о недостаточной насыщенности этих
потребителей.
Эластичность
спроса
на благо
от цены
блага
определяется формулой:
.
При
называется перекрестной эластичность,
при— прямой эластичностью спроса по цене.
показывает на сколько процентов изменится
потребление благапри изменении цены
блага
на 1 %. Положительное значение прямой
эластичности по цене называется
парадоксом Гиффина: изменение цены
блага обуславливает изменение спроса
на него в том же, а не в противоположном,
как обычно, направлении. Для большинства
товаров,
парадокс Гиффина может наблюдаться
только для товаров, у которых.
Полная схема для вычисления всех прямых
и косвенных эластичностей по цена и
эластичностей по доходу была предложена
норвежским ученым Р. Фришем. При изучении
и прогнозировании потребительского
спроса весьма информативными
характеристиками оказываются так
называемые эластичности Е. Е. Слуцкого,
где.
Товарыи
— взаимозамещающие (субституты) при
,
взаимодополняющие при,
независимые при.
На основе данных о значениях эластичностей
Слуцкого могут проводится исследования
возможностей переключения потребительского
спроса при ограниченном предложении
отдельных товаров.
В прикладных
исследованиях спроса и потребления
получила распространение линейная
модель Стоуна – Джири, целевая функция
которой задается в форме
,
где
— коэффициент, задающий приоритет
потребления блага;
— минимальный объем
потребления блага
.
Другие используемые
целевые функции
,
где
— минимальные и максимальные значения
(уровни насыщения) величин,
— весовые коэффициенты;
,
где
— постоянные параметры.
Иногда в моделях
оцениваются только параметры функций
спроса, а целевая функция потребления
непосредственно не задается. Кроме
статических моделей, в которых характер
зависимости спроса от цен и дохода не
меняется с течением времени, разработаны
и динамические модели, где целевая
функция зависит от так называемых
переменных состояний. В случае товаров
длительного пользования соответствующие
переменные интерпретируются как запасы
за счет покупок в предшествующий период,
а в случае остальных товаров – как
психологический «запас» (совокупность
исторически сложившихся привычек
потребителя, влияющих на уровень текущего
потребления).
Математическое
моделирование применяется в анализе
влияния социально-демографических
характеристик на объем и структуру
потребления. В качестве первичной
потребительской единицы в статистике
выступает семья («домашнее хозяйство»).
Поэтому группа моделей (шкалы потребления)
отражают воздействие размера и состава
семьи на структуру ее потребительского
спроса. При сопоставлении индивидуальных
семейных бюджетов расходы (в том числе
и расходы по отдельным статьям бюджета)
необходимо нормировать в зависимости
от половозрастного состава семьи
(соответствующие поправочные коэффициенты
объединяются в единую «шкалу потребления»).
Особенности
дифференциации личного потребления
населения изучаются в рамках модели
дифференцированного баланса доходов
и расходов населения (ДБ), которая
представляет систему таблиц, дающих
детальное описание структуры доходов
населения из различных источников и
структуры расходов в соответствии с
дифференциацией семей по различным
экономическим типам. Разработанный в
1960 – 1970 гг. в СССР и используемый в
Российской Федерации ДБ из всех факторов,
сказывающихся на дифференциации
потребления, практически учитывает
только доход. Наряду с основной схемой
ДБ нужно рассматривать и его расширенную
схему, включающую ряд дополнительных
(примыкающих) таблиц, отражающих
половозрастной состав семей, жилищные
условия населения и др. Число этих
дополнительных таблиц ДБ увеличивается
в соответствии с набором факторов,
определяющих жизненный уровень населения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Дулесов А.С.
1
Гиманова И.А.
1
Мельникова О.Л.
1
Колмакова З.А.
1
1 ФГБОУ ВО «Хакасский государственный университет имени Н.Ф. Катанова»
Рассматривается торгово-посредническая сеть, включающая в себя микрорынки и агентов – участников покупки и продажи товара одного вида. Для принятия решения экономическими агентами в соблюдении баланса между спросом и предложением предлагается построить линии потребительского спроса на основе наличия показателей, таких как цена и объем продаж товара. Решение такой задачи основывается на разработке упрощенной математической модели, описывающей наличие возможных закономерностей распределения статистических данных в процессе функционирования микрорынка. Среди закономерностей рассматриваются нормальное и степенное распределения, не исключая «закон Зипфа». Определена роль коэффициента, который связывает показатели двух микрорынков. Этот коэффициент необходим для оценки участия экономического агента при покупке и последующей продаже товара. Обоснованы возможности применения предлагаемой модели и даны примеры (с иллюстрациями) построения линий потребительского спроса. Функции линейного вида получены при наличии нормального закона распределения объемов продаж, нелинейного вида – при условии соблюдения «закона Зипфа» и степенного закона распределения. Модель позволяет строить линию спроса с её приближением к реально складывающемуся спросу на микрорынке при изменении степени и начальных условий.
моделирование
торгово-посредническая сеть
спрос и предложение
динамика взаимосвязи
1. Кураков Л.П., Игнатьев М.В., Тимирясова А.В. и др. Микроэкономика: учебник для вузов / Под общ. ред. А.Л. Куракова. М.: Изд-во ИАЭП, 2017. 353 с.
2. Поддубный В.В., Романович О.В. Математическое моделирование оптимального рынка конкурирующих товаров в условиях лага поставок // Компьютерные исследования, моделирования. 2012. Т. 4. № 2. С. 431–450.
3. Konigsberg L.W., Frankenberg S.R. Of Typicality and Predictive Distributions in Discriminant Function Analysis. Human Biology Open Access Pre-Prints. 2018. 130. [Electronic resource]. URL: https://digitalcommons.wayne.edu/humbiol_preprints/130 (date of access: 10.10.2019).
4. Стольникова Ю.С., Поливанова А.Е., Шошина В.О., Агишева Д.К., Зотова С.А. Функции спроса и предложения в экономике // Современные наукоемкие технологии. 2014. № 5 (2). С. 200–201.
5. Уфимцев Р. Узел 1. Причина степенных распределений. [Электронный ресурс]. URL: http://www.cognitivist.ru/er/kernel/knots_power_law_01.xml (дата обращения: 10.10.2019).
6. Schmidt D.F., Makalic E. Universal Models for the Exponential Distribution IEEE Transactions on Information Theory. 2009. Vol. 55 (7). P. 3087–3090.
7. Clauset A., Shalizi C.R., Newman M.E.J. Power-Law Distributions in Empirical Data SIAM Review. 2009. Vol. 51 (4). P. 661–703.
8. Jiang B., Jia T. Zipf’s law for all the natural cities in the United States: a geospatial perspective. International Journal of Geographical Information Science. 2011. Vol. 25 (8). P. 1269–1281.
9. Путь воина. Менеджерами не рождаются, менеджерами становятся. Закон Ципфа и фрактальная природа социальных и экономических явлений. [Электронный ресурс]. URL: http://baguzin.ru/wp/zakon-tsipfa-i-fraktalnaya-priroda-sots (дата обращения: 12.10.2019).
Рассматривая логистические процессы, агенты (производители, посредники и конечные потребители) торгово-посреднической сети (ТПС) обращают внимание не только на свои потенциальные возможности, но и на реакцию свободного рынка конкурирующих товаров. Важное место здесь занимают спрос и предложение. В классических моделях микроэкономики [1] рассматривается точка равновесия, образованная пересечением линий спроса и предложения, которая определяет цену товара и объем продаж. Если под воздействием факторов эта точка покидает равновесное состояние и путем управляющих воздействий должна вернуться в исходное состояние или близкое к нему, то речь идет об устойчивости системы. Движение точки имеет колебательный характер с равными по величине отклонениями справа и слева от точки равновесия. В этом случае будем иметь идеальный случай устойчивости, который подтвердится нормальностью закона распределения случайной величины таких показателей, как цена и объем продаж. В реальных условиях функционирования рынка можно предположить, что вид линии и, следовательно, функцию спроса можно построить исходя из покупательского спроса при различных ценах на один и тот же товар. Но вид линии предложения, как правило, неизвестен, и его практически невозможно оценить по наблюдениям за состоянием рынка [2].
Цель исследования заключается в разработке упрощенной математическая модели построения линий спроса с учетом возможных закономерностей распределения статистических данных в процессе функционирования микрорынка для агентов торгово-посреднической сети.
В системе поставок и реализации продукции на спрос и предложение оказывает немаловажное значение количество факторов влияния, что не позволяет четко судить о наличии той или иной закономерности распределения случайной величины [3]. Следовательно, на множестве 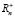
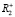
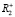
Модель построения линий спроса
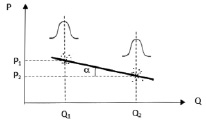
Если представить ТПС в виде графа сети, то его простейшее изображение имеет ребра/ветви – агенты и вершины/узлы – микрорынки, на которых осуществляется процесс купли-продажи. Микрорынки характеризуются показателями: P – цена единицы товара; Q – объем реализации товара при данной цене. Агент, связывающий микрорынки между собой, характеризуется количеством приобретенного и реализованного товара (производитель только реализует товар, конечный потребитель только приобретает его). Соотношение этих показателей позволяет рассчитать коэффициент R указывающий, в каком соотношении находится сложившийся спрос на микрорынках.
Определить коэффициент R можно следующим образом. На каждом из микрорынков, которые связывает агент, следует иметь данные о приобретении товара у поставщика/продавца и о его реализации покупателю, то есть P1,Q1∈?1 и P2,Q2∈?2. Здесь ?1 и ?2 – области данных, принадлежащие соответственно результатам покупки и продажи товара на микрорынках 1 и 2 (рис. 1). Анализ данных каждой из областей следует направить на выявление закономерностей распределения цены и объемов. В этом случае первое, что обычно приходит в голову – проверка на нормальность распределения случайных величин. Если данный закон распределения подтверждается, найти координату в ?1 и ?2 не составляет особого труда, поскольку речь идет о возможности определения математического ожидания или средней величины. Однако часто анализ указывает на наличие асимметрии (что обусловлено инфляционными процессами), то координаты возможно определить через медиану. Определить коэффициент, связывающий показатели двух микрорынков, можно по выражению
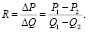
Этот коэффициент представляет собой тангенс угла α наклона прямой, связывающий две координаты, каждая из которых относится к своему микрорынку (рис. 1). Величина R может быть как отрицательной (относящейся к спросу), так и положительной (относящейся к предложению). Единицей измерения коэффициента является ден.ед/объем. Для производителей – 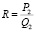
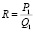
Рис. 1. Линия спроса между микрорынками
Переходя к рассмотрению спроса, сложившегося на микрорынке, построение её линии, которая отвечала бы требования учета практического большинства факторов – сложная задача. Далее будем рассматривать её построение в упрощенной постановке данной задачи.
В простейшем случае линия спроса, определяющая зависимость объема спроса товара от его цены, представляется прямой линией [1, 2], понижающейся с ростом цены:
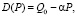
где α – модуль тангенса угла наклона линии (что и R) в координатах цена-спрос (P, Q), Q0 – спрос при нулевой цене.
Пример 1. Построение линии спроса линейного вида. Имеется две координаты: (144; 0) и (84; 6). Определим коэффициент: 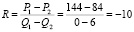
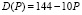
В действительности спрос D(P) не линеен (одна из его функций представлена в [4]). Когда цена приближается к нулю, объем очень быстро возрастает, а при значительном увеличении цены – медленно стремится к нулю, оставаясь положительным. Если принять во внимание линейную модель спроса (2), то она описывает простейшее приближение линии спроса, достаточно адекватное реальности лишь в окрестности точки рыночного равновесия, когда спрос и предложение сбалансированы. В данном случае если спрос на товар полностью удовлетворен, то выручка от продажи товара (как фактор будущего предложения) определяется по формуле: I = P·D(P).
Важной характеристикой спроса D(P) является следующее: в процессе купли/продажи на микрорынке агенты стремятся обеспечить покупательский спрос и при этом добиться максимальной прибыли путем соответствующего регулирования цены товара. В этом процессе становится очевидным факт того, что слишком высокие цены приведут к снижению покупательского спроса на товар и уменьшат объем продаж с соответствующим понижением прибыли. С другой стороны, попытка установить слишком низкие цены сделает рынок нерентабельным для продавцов. Следовательно, критерий оптимальности поведения микрорынка направлен на соблюдение требования поддержания покупательского спроса при цене, обеспечивающей максимальную прибыль продавцов, т.е. максимальную рентабельность микрорынка. Эти требования не исключают необходимости построения линии спроса для каждого агента, поскольку он, будучи задействованным на микрорынке, определяет спрос. Следовательно, на микрорынке каждый агент на будущее будет придерживаться тактики, опирающейся на собственный спрос, и ему предстоит строить для себя функцию спроса. Тем самым будем иметь к рассмотрению несколько линий спроса. Исходя из сложившейся ситуации на микрорынке в результате купли/продажи сформируется новый спрос с координатами, которые образуют обобщенный спрос. Данный спрос определяет количество благ, которые получат/приобретут все агенты на микрорынке в течение заданного времени и при сложившихся условиях. В такой постановке решение задачи определения координат обобщенного спроса и построения его функции может послужить основанием для принятия к анализу полученных результатов всеми агентами микрорынка. Следовательно, можно рассчитывать на упрощение расчетов распределения товарных потоков в ТПС.
Далее рассмотрим процедуру построения линии спроса нелинейного вида. Как было отмечено выше, наблюдение за спросом – «размазанное» поле точек в пространстве и во времени. Кроме пространственной и временной индивидуальной «размазанности» присутствует коллективная, когда множество факторов распределяются в пространстве, а множество событий – во времени [5]. Анализ коллективного явления предполагает помимо параметров P и Q рассматривать некоторые дополнительные измеримые параметры, которые можно характеризовать некоторой совокупностью распределений. Среди них часто выделяют два класса распределений: экспоненциальное и степенное.
Если имеем в распоряжении данные, относящиеся к рассматриваемым параметрам (не имеющим нулевых значений), то наиболее простой и во многих случаях подтверждающейся гипотезой является гипотеза о том, что параметр (например, Q) имеет нормальное распределение (рис. 1). Аналогично, если анализ указывает на то, что рассматриваемый параметр чаще принимает малые значения, нежели большие, то, вполне возможно, подтвердится гипотеза, когда параметр отвечает экспоненциальному распределению [6].
Тем не менее первое предположение о нормальности распределения считается главной гипотезой [5]. Это связано с тем, что механизм развития нормального распределения выглядит фундаментально просто и элегантно, чего нельзя сказать об упомянутых альтернативах. Простота обеспечивает универсальность механизма, поскольку можем предположить его действие во многих случаях, когда рассматриваемое явление характеризуется параметрами, демонстрирующими колоколообразные распределения.
В подтверждение упомянутого рассмотрим следующий пример. Пусть на микрорынке присутствует несколько агентов (производителей и посредников). Обозначим начальный момент времени, когда агенты не имеют в своем распоряжении ресурсов, то есть количества товаров, подлежащих купле/продаже. Запускаем механизм купли/продажи и под воздействием факторов спроса количество товара случайным образом распределяется между агентами. Очевидно в таком случае будем иметь нормальное распределение и, вполне возможно, с наличием асимметрии. Если аналогичные процессы будут протекать на всех микрорынках, то распределение товарного потока по всей ТПС также будет нормальным. Данное утверждение основано на наличии спроса конечных потребителей, когда товар между ними распределяется случайным образом, в зависимости от их предпочтений.
Еще один пример. Пусть на одном из микрорынков рассматривается вопрос об управлении товарным потоком. В данном случае количество товаров будет попадать на другие микрорынки и по истечении некоторого времени распределение количества товара на них будет экспоненциальным, а не нормальным.
Разница между распределениями товарного потока заключается в том, что в первом примере количество товара на микрорынке связано со спросом (чем чаще возникает спрос, тем больше представлено на рынке товара), тогда как во втором – частота продаж/покупок не зависит от имеющегося количества товара. Очевидно следующее: в первом случае спрос определяет количество реализованного товара, а во втором – скорее всего формируется агентами.
Кроме упомянутых распределений существует особый класс распределений – степенной [7]. В сфере потребления он определяет распределение объема собственных средств граждан некоторого общества. В ситуации, когда гражданин распределяет собственные средства нельзя сказать, что он это делает случайным образом, тем не менее множество граждан определяют спрос на товарном рынке. Не исключено при этом не только нормальное или экспоненциальное, но и степенное распределения, уравнение которого можно записать в таком виде:
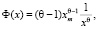
где θ > 1 – показатель степени, xm – минимальное значение наблюдаемого статистического параметра x. Поскольку степенное распределение не должно иметь нулевого значения параметра, то необходимо вести нижнюю границу возможных значений параметра, иначе распределение не сходится.
Важное значение в (3) принимает показатель степени. Если принять θ = 2, то будем иметь известный «закон Зипфа» [8, 9]:
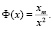
Форма данного распределения схожа с формой экспоненциального: малые значения параметра P встречаются чаще (покупатель предпочитает брать больше товара с низкой ценой, нежели с высокой), кривая распределения спадает. Справедливость (4) уместна, когда при покупке товара, покупатель рассчитывает на объем денежных средств C, используя которые он может купить xm по самой высокой цене Pmax. Тогда (4) можно переписать в виде:
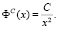
Функция (5) имеет степенной вид, то есть относится к степенному закону:
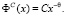
Константа C, так же как и θ, имеет фиксированное значение, но может изменяться экспоненциально: 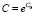
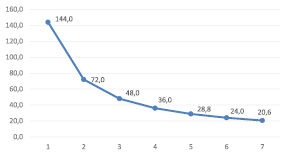
Построенная кривая спроса (5) на каждом из рассматриваемых участках характеризуется эластичностью. Поскольку нас интересует эластичность по цене, её определяют по формуле:
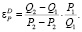
Далее представим примеры построения линий спроса, используя функцию (3).
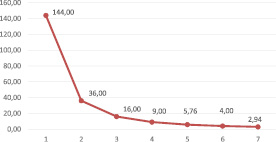
Пример 2. Построение линии спроса вида 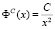
Таблица 1
Решение задачи построения
линии спроса
|
№ п/п |
Количество x (или Q) |
|
|
|
1 |
1 |
144,00 |
– |
|
2 |
2 |
36,00 |
1,3 |
|
3 |
3 |
16,00 |
0,9 |
|
4 |
4 |
9,00 |
0,8 |
|
5 |
5 |
5,76 |
0,7 |
|
6 |
6 |
4,00 |
0,7 |
|
7 |
7 |
2,94 |
0,6 |
Линия спроса изображена на рис. 2.
Рис. 2. Линия спроса
Рис. 3. Линия спроса
Поскольку спрос по цене в данном примере не эластичен, то есть 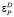
Пример 3. Построение линии спроса вида: 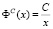
Таблица 2
Решение задачи построения
линии спроса
|
№ п/п |
Количество x (или Q) |
|
|
|
1 |
1 |
144,00 |
– |
|
2 |
2 |
72,0 |
2,0 |
|
3 |
3 |
48,0 |
1,5 |
|
4 |
4 |
36,0 |
1,3 |
|
5 |
5 |
28,8 |
1,3 |
|
6 |
6 |
24,0 |
1,2 |
|
7 |
7 |
20,6 |
1,2 |
Линия спроса изображена на рис. 3.
Как видно, на рис. 3 «тяжелый хвост» отсутствует. Спрос по цене в данном примере эластичен, 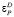
В конечном итоге нельзя однозначно сказать о том, какой вид будет иметь линия спроса, которая необходима агенту как некоторое условие для совершения сделок покупки/продажи. Для более точного результата все-таки требуется выполнить процедуру обработки статистических данных с тем, чтобы подтвердить гипотезу о наличии закона распределения случайной величины.
Заключение
Построение линии потребительского спроса для агентов торгово-посреднической сети предполагает наличие математической модели, а по существу – функции спроса. Она позволяет агенту торгово-посреднической сети определиться с ценой и объемами продаж/покупки на её микрорынках. Построение функции спроса основывается на наличии статистических данных параметров рынка (цена и объем продаж) и их обработке. Выдвигая гипотезу о возможном распределении случайной величины рассматриваемого параметра, её подтверждение – основа для построения функции спроса. В тех случаях, когда рынок нестабилен, довольно сложно решить задачу о справедливости наличия закона распределения случайной величины. Здесь прослеживается вариант, когда с некоторой долей уверенности, при наличии одной или двух координат на евклидовом пространстве (имеющих некоторое усредненное или медианное значение), можно построить функции спроса в виде прямой или кривой линии.
Представленная в данной работе математическая модель построения линий спроса, в своей основе базируется на уравнении степенного распределения. Выдвигается подтверждённое примерами предположение о том, что степень определяет не только связь цены с объемом, но и обосновывает взаимоотношения агентов на микрорынке торгово-посреднической сети, пусть даже и в весьма упрощенной постановке задачи. Изменяя степень и начальные условия, модель позволяет строить линию спроса с её приближением к реально складывающемуся спросу на микрорынке.
Исследование выполнено при финансовой поддержке РФФИ и республики Хакассия в рамках научного проекта № 19-47-190001.
Библиографическая ссылка
Дулесов А.С., Гиманова И.А., Мельникова О.Л., Колмакова З.А. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПОСТРОЕНИЯ ЛИНИИ ПОТРЕБИТЕЛЬСКОГО СПРОСА ДЛЯ АГЕНТОВ ТОРГОВО-ПОСРЕДНИЧЕСКОЙ СЕТИ // Современные наукоемкие технологии. – 2019. – № 11-2.
– С. 264-269;
URL: https://top-technologies.ru/ru/article/view?id=37802 (дата обращения: 29.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СПРОСА
© Дамиров В.М.*
Сарапульский политехнический институт (филиал)
Ижевского государственного технического университета, г. Сарапул
В статье рассмотрены проблемы доработки предложенной ранее многокритериальной модели, предназначенной для моделирования спроса потребителей на группу товаров, выпускаемых предприятием. Предложенная ранее модель позволяет учитывать основные факторы, влияющие на спрос.
Разработанная на основе нее новая математическая модель позволяет провести моделирование спроса для группы потребителей с различным уровнем доходов, минимизировать себестоимость продукции и максимизировать прибыль. Разработанная модель является моделью нечеткой многокритериальной оптимизации. В статье дана постановка нечеткой задачи оптимизации для целевой функции с интервальными коэффициентами и рассмотрены некоторые из методов ее решения, а именно поиск компромиссного решения и определение компромиссного решения при помощи метода редукции.
Также в статье была произведена общая постановка задачи многокритериальной оптимизации, рассмотрены методы решения данной задачи, а именно метод приведения ее к однокритериальному виду и метод декомпозиции. Для решения поставленной нечеткой многокритериальной задачи моделирования спроса потребителей был выбран метод декомпозиции.
В условиях мирового экономического кризиса, при наблюдающемся спаде производства и уменьшении доходов потребителей, а соответственно и их покупательной способности, очень важно иметь наиболее четкий прогноз спроса на группу товаров, выпускаемых или продаваемых предприятием.
Под спросом будем понимать объем товара, который может быть реализован на рынке в определенный период времени по заданной цене.
Для прогнозирования спроса можно использовать математическое моделирование.
Целью работы является повышение эффективности управления предприятием, за счет планирования выпуска продукции.
Для достижения цели была поставлена задача — разработать математическую модель для исследования потребительского спроса на группу товаров, выпускаемых предприятием.
* Доцент кафедры «Технология машиностроения металлорежущие станки и инструменты», к.п.н.
1. Анализ основных факторов, влияющих на спрос
Спрос на продукцию серьезно ограничивает объем ее производства, т.е. влияет на предложение товаров предприятия потребителям. На спрос может влиять множество факторов, рассмотрим их более подробно (рис. 1).
И Т.П.
Рис. 1. Факторы, влияющие на спрос
Сразу следует отметить, что влияние внешнеэкономических факторов на спрос учитывать будет достаточно сложно, поскольку доля влияния данных факторов может существенно колебаться в зависимости от видов товаров, состава населения, мест продажи товаров и т.п. Кроме того само влияние данных факторов на спрос достаточно сложно определить как при помощи математических методов, так и при помощи методов экспертных оценок.
Процент влияния факторов каждой категории на спрос показан на рис. 2.
Поскольку, как уже говорилось выше, влияние внешнеэкономических факторов достаточно сложно учесть и процент их влияния на спрос, как
можно увидеть на рис. 2, не велик, то в дальнейшем будем рассматривать только экономические факторы.
10%
Рис. 2. Влияние факторов на спрос
При этом необходимо учитывать то, что значение данных факторов для каждого товара также может значительно колебаться.
Следовательно, необходимо разработать математическую модель для моделирования потребительского спроса на группу товаров, выпускаемых предприятием. При этом данная модель должна позволять учесть не только влияние экономических факторов на спрос, но и долю такого влияния для каждого из товаров.
2. Постановка задачи
Рассмотрим поставленную перед нами задачу, на содержательном уровне ее можно описать следующим образом: потребитель при фиксированной цене и растущем доходе сначала увеличивает потребление данного товара до некого максимального значения, а затем дальнейший рост дохода ведет к снижению потребления данного товара до некого оптимального уровня. Снижение вызывается, во-первых, ростом затрат на транспортировку и хранение товара и ограниченностью возможностей для хранения запасов; во-вторых, перераспределением растущего дохода в пользу более дорогих товаров, которые становятся доступны по мере роста благосостояния потребителя [1].
Если формализовать данную задачу то можно прийти к известной «задаче о рюкзаке»: имеется совокупность объектов, обладающих двумя признаками, необходимо составить набор таким образом, чтобы максимизировать оценку по одному из признаков, при существующем ограничении на второй признак. Задача о рюкзаке бывает двух типов — дискретная задача о рюкзаке и непрерывная задача о рюкзаке. В первом случае все предметы неделимы, а во втором делимы.
В формализованном виде постановка задачи будет строиться на следующих утверждениях.
1. Покупатель собирается потратить некую денежную сумму Ь на покупку множества товаров X = {хь х2, …, хп}.
2. Товары X = {х1, х2, ., хп} продаются по цене р1, р2, ., рп соответственно, т.е. каждому элементу множества X соответствует элемент множества Р = {^1,Р2, …,Рп}.
3. Каждый товар из множестваX = (xb x2, xn} имеется максимальный объем Q = (qb q2, …, qn} соответственно.
4. Считается, что покупка каждого товара характеризуется некоторым коэффициентом полезности С = (Ci, C2, …, Cn} соответственно.
3. Параметризация задачи
Разработаем на основе предположений 1-4 математическую модель для проведения моделирования спроса. Предположения 1 и 2 можно представить виде следующего ограничения(1):
-b (i)
i=i
Предположение 3 дает более широкие возможности для имитационного моделирования, поскольку предлагает учитывать максимальный объем каждого товара. Ограничение, соответствующее данному предположению приведено ниже (2):
■x- ^ qt (2)
где qt — максимальный объем /-го товара.
Последнее предположение позволяет сформировать целевую функцию, разрабатываемой модели (3):
n
ZC‘x‘ ^ max (3)
i=i
При этом под коэффициентом полезности будем понимать некое обобщенное значение, на основании которого потребитель принимает решение
о покупке того или иного из товаров, выпускаемых предприятием.
Данный коэффициент должен учитывать следующие параметры:
— качество товара;
— цена взаимозаменяемого товара;
— цена сопрягаемого товара;
— важность товара для потребителя.
— и т.д.
Представим все факторы, влияющие на спрос i-ro товара, учитываемые в разрабатываемой модели в виде множества — Fi = (F1i, F2i, ., FKi}.
Логично предположить, что коэффициент полезности i-го товара, можно рассчитать по следующей формуле:
С- =± F j=1 ij
Однако в данном случае возникает проблема неоднородности значений показателей Fij; действительно, некоторые из них представляют собой количественные показатели, а некоторые качественные.
Для определения значений нечисловых параметров предлагается использовать пятибалльную шкалу, где 5 — самая высокая оценка, а 1 — самая низкая.
Однако, даже после приведения качественных показателей к количественному виду, возникает проблема неодинаковой размерности показателей; следовательно, необходимо привести показатели в безразмерный вид.
3.1. Приведение параметров к безразмерному виду
Как уже было сказано выше, следующим шагом для получения коэффициента полезности товара является приведение всех параметров к единому безразмерному виду.
Для этого можно использовать следующую функцию (5), приведенную В [2].
fj'(X) =
/М — fi (X,.)
Для позитивно ориентированных критериев
М т
~ (5)
/ (X.) — f т
,1— Для негативно ориентированных критериев
/* М у’ т
1 /
где//(Х,) — значениеу-го критерия для вариантаX, в безразмерном виде;
/(X) — значение у-го критерия для варианта X, в определенных единицах измерения;
гМ
/ — максимальное;
/т — минимальное значения критерия / на определенном множестве альтернатив {X,}.
Таким образом, множество показателей Fi будет преобразовано в безразмерное множество Fi’ следующим образом (6) согласно (5).
Р у = (F1M-F1,) / (F1M-Fr) (6)
3.2. Применение метода экспертных оценок для получения весовых коэффициентов
После приведения значений к безразмерному виду, необходимо определить весовые коэффициенты каждого из параметров для каждого из исследуемых товаров. Для расчета весовых коэффициентов можно использовать метод экспертных оценок, а именно: метод ранжирования.
На сегодняшний день данный метод применяется достаточно часто как в системах поддержки принятия решений, так и в других областях. Данный метод описан во многих источниках, например, в [2].
Содержательная постановка задачи, метода ранжирования, может быть сформулирована следующим образом. Из множества существующих вариантов решений надо выбрать наилучший, с учетом одного свойства, которое характеризуется соответствующим качественным критерием. Для решения этой задачи методом ранжирования экспертам может быть предложено сравнить варианты альтернативных решений на основе учета отдельного свойства /. При этом каждому варианту эксперт должен присвоить ранг (номер), который увеличивается с уменьшением оцениваемого свойства [2]. Рассмотрим основные моменты данного метода, согласно [2].
Пусть есть п вариантов решений, отдельное свойство I оценивает т экспертов. Обозначим через X1/ ранг /-того свойства/-го варианта в оценке /-го эксперта. Сумма рангов в ранжирования 1-го эксперта:
X/ =ЦхУ = 0.5п(п +1) (7)
/=1
При одинаковой оценке нескольких вариантов, эксперты должны придерживаться следующего правила: вариантам с одинаковой оценкой придается ранг, равный среднему арифметическому значению мест, которые они между собою делят. По результатам опрашивания экспертов строится матрица X/, что отображает результаты оценок экспертов. Элементом матрицы будет значения Xу.
Наилучший вариант А будет тот, который соответствует условию:
шш^/} (8)
где X / — суммарный ранг/-го варианта по свойству /.
т
т1
X/ =Х X1/ (9)
Необходимый вариант обработки результатов опроса экспертов — определение их согласованности. Для этого рассчитывается коэффициент конкордации:
/ 12Б1
т
.2,_3 (10)
‘(п3 -п) -т’У1Т1
/=1
При полном согласии экспертов коэффициент равен единице, при полном несогласии нулю, т.е. 0 < К < 1 чем ближе он к единице, тем согласованней мнения экспертов.
Далее рассчитывается дисперсия рангов по объектам Б:
Б1 = £а а = (X/ -Xсер)2 = 0,5т(п +1) (11)
/=1
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
/=1
Вектор оценки одного эксперта:
м
Т ) (12)
где — число повторов ^-ранга в ранжировании /-го эксперта.
Существует два метода взвешивания критериев: нормирование рангов и перевод рангов в диапазон возможных значений. Для определения весовых коэффициентов каждого из факторов предлагается использовать первый метод.
х, преобразуется в х/:
х,’ = (ш * п) — х, (13)
Значение весовых коэффициентов считается по формуле:
х<
р, =
х (14)
К]
,=1
После проведения экспертного оценивания и получения весовых коэффициентов критериев множество .Р/ преобразуется в множество Г», каждый элемент множества рассчитывается по формуле (14):
РУ’ = ¥,’ -р, (15)
3.3. Получение коэффициента полезности товара при помощи метода линейной свертки критериев
После получения весовых коэффициентов остается только получить из множества параметров коэффициент полезности товара, для этого можно использовать метод линейной свертки критериев (13), также описанный в [2].
V, =£ а, / (А,) (16)
]=1
где — степень важности критерия/;
/¡(А,) — оценка параметра А по /-му критерию.
В данной статье предлагается степенью важности считать весовой коэффициент критерия.
Следовательно, коэффициент полезности / -го товара С, можно рассчитать по формуле (17):
С, =&», (17)
,=1
3.4. Математическая модель задачи Таким образом, получена следующая модель задачи (18):
п
^С,х, ^ тах ¡=1
с, =Х р %
^ (18)
п
X РіХ — Ь
І=1
Хі < д,, і =1, …, п Хі > 0, і = 1, …, п
где С — коэффициент полезности цена ¡-го товара.
Рис. 3. Схема имитационного моделирования спроса
Разработанная модель является моделью задачи линейного программирования. Наиболее подходящим методом для решения данной задачи
является симплекс метод. Постановку задачи симплекс метода можно найти, например, в [3-5].
Данная модель отличается от предложенных ранее моделей, например В [1], наличием дополнительного ограничения, в котором учитывается максимальный объем товара, которое позволяет при проведении моделирования отсеять неподходящие для предприятия варианты.
Также в разработанной модели в качестве коэффициента полезности выступает не абстрактная функция полезности, как в [1], а конкретное значение, которое учитывает степень влияния каждого экономического фактора на спрос данного товара. При этом следует отметить, что список таких факторов является не постоянным и может меняться в зависимости от группы товаров. Однако при проведении моделирования одной группы такой список должен быть одинаков для каждого из товаров, при этом весовые коэффициенты одного и того же фактора могут существенно отличаться в зависимости от товара.
Общая схема имитационного моделирования при помощи предложенной модели показана на рис. 3.
Данный метод целесообразней всего использовать при анализе возможности изменения цены на группу товаров, которое выпускает предприятие, в процессе в процессе всего жизненного цикла товаров.
II. Нечеткая многокритериальная модель спроса
Рассмотрим предложенную ранее модель, предназначенную для проведения моделирования спроса на группу товаров выпускаемых предприятием (19).
Основной целью такого моделирования является повышение эффективности управления предприятием.
n
^CjXj ^ max
/=1
YjPXi <b (19)
/=1
Xi < qi, i =1, …, n xi > 0, i = 1, …, n
где Ci — коэффициент полезности i-го товара;
Pi — цена i-го товара;
Xi — объем i-ro товара, который купит потребитель;
b — доход;
qt — максимальный объем i-ro товара.
Коэффициент полезности товара учитывает основные факторы, влияющие на спрос, и рассчитывается с использованием медов ранжирования и линейной свертки критериев.
1. Максимизация прибыли и минимизация себестоимости
Предложенная ранее модель не учитывает нескольких важных моментов, а именно:
1. Цена товара не должна быть ниже себестоимости, поскольку такая цена даже при достаточно большом спросе, приведет к убыткам предприятия, что не допустимо, поскольку, основной целью данной работы является повышение эффективности управления предприятием. Следовательно, в предложенную ранее модель необходимо ввести еще одно ограничение, которое будет учитывать зависимость цены товара от себестоимости.
Р, > Б,
где- себестоимость /’-го товара.
2. С точки зрения эффективности управления предприятием, основной целью имитационного моделирования спроса, является максимизация прибыли самого предприятия. Данное утверждение можно необходимо представить в виде следующей целевой функции:
п
X РЯ‘ ^ тах
i =1
3. Кроме максимизации прибыли предприятия, эффективное управление предполагает минимизацию затрат на изготовления той или иной продукции, т.е. минимизацию себестоимости. Следовательно, в предложенную ранее модель добавляется еще одна целевая функция:
п
^ шп
i =1
Однако при рассмотрении себестоимости не рационально ограничиваться одним значением. Необходимо указать интервал значений для себестоимости, т.е. Б, е … Б,и],, = 1 … п
Такая задача оптимизации называется — нечеткой.
4. Также необходимо учитывать, что разрабатываемая имитационная модель предназначена для применения на конкретных предприятиях. Следовательно, количество продукции определенного вида на каждом из складов конечно, а значит, в данной модели необходимо учитывать и объемы складов. Ограничение на склад можно описать следующим образом:
±4, * о
, =1
где О — размер склада.
Проведем анализ основных методов нечеткой оптимизации, которые можно применить для минимизации себестоимости, описанных в [1].
1.1. Постановка задачилинейного программирования с нечеткими целевыми функциями
Предположим что только один элемент из пространства [SjL … SiU] х [S2L … S2U] х … х [SnL … Snu] является истинным вектором коэффициентов целевой функции, минимизации себестоимости. Тогда данная задача имеет единственный вектор целевой функции, но возникает проблема, которая содержит бесконечное множество целевых функций следующего вида:
z(q) = STq ^ min (20)
Данные функции должны быть минимизированы одновременно для q е Q, где Q = {q: q < O; q> 0}. Все векторы S е Rn из ограниченного интервала S0 = {s: SL< s < su}; slT = {siL, s^L, …, SnL}; suT ={siU, S2U, …, SnU}
должны рассматриваться как параметры.
«Полное» решение задачи линейного программирования с интервальными коэффициентами вида (21):
min{z(q) = STq | q: q < O; q > 0} (21)
определяется как:
E = {q eQ 13q eQ, 3st e S 0S’Tq > Sl_q, Vq eQ }
Нахождение такого «полного» решения является не только затруднительным, но и требует больших затрат. Поэтому достаточно часто в задачах оптимизации с несколькими целевыми функциями вместо множества эффективных решений ищут одно компромиссное [1].
Определение компромиссного решения приводится в [1].
Пусть функция Н:Р^Я-функция предпочтения для задачи (21), то элемент q е Q называется компромиссным решением задачи (20), если q е Ей H(q*) > H(q), Vq е Q.
1.2. Поиск компромиссного решения
Для определения компромиссного решения задачи линейного программирования существуют различные функции, называемые функциями предпочтения. Данные функции преобразовывают множество целевых функций в единственную компромиссную целевую функцию.
Простейший метод использующий данный подход и описанный в [1], заключается в том что выбирается одно значение st для каждого интервала [SiL … S,u] и вместо задачи (20) необходимо решить следующую задачу линейного программирования:
min{z (q) = £Stqt | q <O ;q >o} (22)
i =1
Исключив два крайних случая, максимальный и минимальный, получим:
zmin SL q, zmax SU q
Для получения компромиссного решения s необходимо выбрать в каждом интервале значение с наибольшей вероятностью появления. Но если у ЛПР нет достаточно сведений для принятия такого решения, то можно выбрать середину данного интервала [SiL … S,u] получим:
z = 0.5[Zmin(q) + Zmax(q)] = 0.5[SlT + SuT]q (23)
Дальнейшим развитием такого подхода является использование целевой функции, которая базируется на решающем правиле Гурвица.
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Критерий Гурвица основан на следующих двух предположениях: природа может находиться в самом невыгодном состоянии с вероятностью 1 — а и в самом выгодном — с вероятностью а, где а — коэффициент доверия [1].
z(q) = (1 — T)Zmin(q) + TZmax(q) = [(1 — t)SlT + TSj]q (24)
где т — параметр оптимизма, который отражает отношения к риску со стороны ЛПР.
Основным недостатком описанных выше подходов является то, что все они работают не с целым интервалом S0, ас отдельными его значениями.
Если у ЛПР нет возможности выбрать только одно какое-либо значение из интервала S0, необходимо использовать косвенный путь построения компромиссной целевой функции описанный в[1].
Сначала происходит фиксация множество состояний природы:
Zj, j = 1 … w
как состояний неопределенности. Выбор состояний происходит таким образом, что бы у ЛПР была возможность:
1) привести вероятность СОСТОЯНИЙ p(Zj)
2) наиболее точно определить параметры для каждого из состояний.
Исходя из всего вышесказанного, используя подход Бернулли, ожидаемая величина:
q=^LsTjqp(z j) =YjsTp (zjq (25)
j=1 j=1
выбирается функцией компромисса.
Так как sp(zj) е S0, для каждого из векторов состояний и для любого распределения вероятностей {p(zj)}, то любая функция компромисса при-
ведет к эффективному решению оптимизационной задачи. Но не решенным остается вопрос о возможности получении необходимой информации о значениях (р^)}, ^ }[1].
2. Общая постановка задачи
Необходимо провести моделирование спроса на группу товаров, выпускаемых предприятием для потребителей с разным уровнем дохода.
Основной целью данного моделирования является повышение эффективности управления предприятием.
Пусть 3 = (1 … т} множество потребителей с доходом
На основе проведенного ранее анализа автором сформулирована следующая математическая модель, предназначенная для имитационного моделирования спроса:
т п
X Т£уху ^ тах
] =1 < =1
п
XРЛ< ^ тах
I =1
п
£ ^ шп
I =1
£ Тр,х,<Ъ (26
] =1 < =1
Ъ, * О
1 =1
р, > 8
8, е [# … 8,и]
Ху < д,, = 1, …, п,] = 1, …, т Ху > 0, , = 1, …, п,] = 1, …, т
Данная модель является моделью многокритериальной нечеткой оптимизации.
В общем, виде задача многокритериальной оптимизации может быть определена следующим образом.
2.1 Постановка задачи многокритериальной оптимизации
Для каждого объекта (проекта, минимизация затрат и т.п.) вводят вектор — критерий П = (Ж1, Ы2, …, Ыт} в котором частный критерий Щ представляет функцию параметров х1, х2, …, хп (которые определяют, например, характеристики управлений проектом и т.п.). Функциональная зависимость частных критериев от параметров задачи задается, и тогда основная математическая модель многокритериальной оптимизации будет сформулирована так:
(Х) £ тпхЯ 1 = 1т
[ X = )Х/Х 6 кп, Че (Х) ^ о) е е1,V,V < п
В этой модели X — множество допустимых решений, удовлетворяющих определенным ограничениям, которые даны в виде системных неравенств Че (Х) < 0 накладываемых на векторпараметров х =(Х1, Х2, …, Хп }[2].
Функция Л (Х1, Х2, …, Хп) будет называться у-той целевой функцией, а вся совокупность (Х1), ., /т (Хт) образует векторную целевую функцию многокритериальной оптимизации [2].
2.2. Преобразование из многокритериальной в однокритериальную задачу
Одним из возможных путей решения многокритериальных задач является путь преобразования из многокритериальной в однокритериальную задачу. Рассмотрим более подробно такой подход, приведенный в [3].
Отметим, что поскольку Е(х) является неким вектором, то любые компоненты Е(х) являются конкурирующими и отсутствует некое единое решение поставленной задачи. Вместо него для описания характеристик целей используется концепция множества точек неулучшаемых решений (так называемая оптимальность по Паретто). Неухудшаемое решением будем называть такое решение, при котором улучшение в одной из целей приводит к ухудшению в другой.
Рассмотрим данную концепцию детальней. Пусть существует некая область допустимых решений О в параметрическом пространстве х е Х. Данное пространство удовлетворяет все принятые ограничения, т.е.:
О = (х е Яп}
при заданных в (10) ограничениях.
Отсюда возможно определить соответствующую область допустимых решений для пространства целевых функций Л.
Л = {у е Я„}
где у = Е(х) при условии Х е О.
Определение точки неулучшаемого решения приведено в [3].
Точка х е О является неулучшаемым решением, если для некоторой окрестности х нет некого Ах такого, что (х + Ах) ейи:
Е^х’ + Ах) < Е^х*), , =1, ., т Е1(х* + Ах) < Е}(х*), для некого у
Поскольку любая из точек пространства О, то есть пространства, не имеющего неухудшаемых точек, является точкой, в которой любое улуч-
шение может быть достигнуто во всех выбранных целях, то ясно, что такая точка не представляет никакой ценности. Следовательно, многокритериальная оптимизация должна включать в себя определенную генерацию и выбор точек с неулучшаемыми решениями [3].
2.3. Декомпозиция многокритериальной нечеткой задачи моделирования потребительского спроса
Следующим путем для решения многокритериальной задачи является ее декомпозиция, т.е. разбиение, на отдельные однокритериальные задачи оптимизации. Пример такой декомпозиции можно найти в [4].
Именно данный подход и предлагается использовать для решения разработанной имитационной модели спроса.
Сначала решим две однокритериальных задачи оптимизации для минимизации себестоимости и максимизации прибыли. При этом необходимо помнить, что первая задача является задачей нечеткой оптимизации.
1. Минимизация себестоимости.
п
£ 8^1 ^ тт
I =1
Ъ, * О (29)
I =1
Чг ^ 0
8, е & … Б,и]
2. Максимизация прибыли:
п
XР-Ч- ^ тах
‘=1 > 8 (3°)
Рг > 8
Рг > 0
После чего на каждом такте расчета у будем последовательно решать однокритериальную задачу моделирования спроса:
п
^СуХу ^ тах
1=1
1^Р<Ху <Ьу (31)
1=1
Ху < Чг, г = 1, …, п,у = 1, …, т Ху > 0, г = 1, …, п,у = 1, …, т
Как мы видим, разработанные модели тесно связаны между собою общими параметрами, поэтому на любом шаге моделирования спроса может возникнуть необходимость пересчитать показатели, получаемые в моделях (29) и (30).
Каждую из моделей (29)-(31) можно привести к целочисленному виду, поэтому при их решении целесообразно использование методы линейной целочисленной оптимизации.
Ш. Применение методов мелкозернистых вычислений
в однородных вычислительных средах для моделирования спроса с использованием численных методов и нейронных сетей
Предложено рассмотреть цену не как параметр, а как функцию многих переменных, в число которых входят и затраты на производство. При этом затраты на производство также представлены в виде монотонной для каждой переменной и имеющей разрывы на координатных плоскостях функции, которая стремится к минимуму. Для минимизации затрат предложено использовать численные методы, а именно метод наискорейшего спуска. Построен алгоритм нахождения минимума с использованием данного метода.
Для исследования и моделирования цены предлагается использовать нейронные сети. Рассмотрена теорема Колмогорова, на котором базируется такое исследование, и ее улучшение, которое позволяет применить данную теорему на практике.
После проведенного исследования построенной модели был сделан вывод о невозможности ее расчета последовательно и предложено использовать методы мелкозернистых вычислений в однородных средах. Кроме того, были выделены основные потоки для параллельных вычислений.
Одним из важнейших факторов, влияющих на разработку стратегии производственного предприятия на рынке готовой продукции, является спрос потребителей. Так как для точного планирования объема выпускаемой продукции нужно четко оценивать ситуацию на рынке, то есть проводить анализ спроса и исследования конкурентоспособности товаров, выпускаемых предприятием.
Произвести анализ спроса теоретически очень сложно, так как любое использование статистики, социологических исследований и тому подобное дает лишь приблизительный результат.
Исследование спроса на группу товаров, выпускаемых предприятием, является основой для управления хозяйственной деятельностью предприятия, планирования продаж и закупок и ценообразования на продукцию.
Для разработки стратегии развития предприятия необходимо не только учитывать текущий спрос на продукцию, но и проводить его моделирование.
Для моделирования спроса можно использовать следующие методы:
— статистическое моделирование;
— обобщённые математические модели или принципы (системный анализ в узком смысле [1]);
— аксиоматические методы моделирования (системный анализ в широком смысле или системный подход [1]).
— методы экстраполяции.
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Применение методов статистического моделирования базируется на применении случайных чисел. А именно, под статистическим моделированием подразумевается численный метод решения математических задач, при котором искомые величины представляют вероятностными характеристиками какого-либо случайного явления, это явление моделируется, после чего нужные характеристики приближённо определяют путём статистической обработки «наблюдений» модели [2].
Однако в сложных процессах и явлениях, к каковым можно отнести и моделирование спроса, часто проявленные и зафиксированные статистические параметры не могут быть признаны решающими или определяющими. Хотя данные методы и имеют механизмы ранжирования параметров. Кроме того статистические методы почти не приспособлены для выявления существенных и неизвестных ранее факторов.
К другим методам математического моделирования относятся математические модели (линейное и нелинейное программирование, марковские цепи и процессы и другие), которые позволяют выявлять существенные и неизвестные ранее факторы процесса или явления. Но любая математическая модель может применяться только в определенных границах, т.е. имеет ограничения по применению. Именно поэтому в системном анализе данный подход описывается как системный подход в «узком смысле» [1].
Использование системного подхода «в широком смысле» [1], то есть с позиций заимствования его аксиоматических методов для моделирования экономических процессов и явлений[1], хотя и позволяет провести более подробное моделирование, является достаточно сложно формализирован-ным методом, поскольку предполагает переход к более широким обобщениям в экономической науке путём совершенствования аксиоматических принципов для моделирования (системный подход [1]).
Экстраполяция базируется на распространении сложившихся в прошлом тенденций на будущее. Однако такой подход лучше всего применять при краткосрочном прогнозировании, поскольку рынок готовой продукции в наше время достаточно нестабилен. Особенно это касается продукции, не являющейся товарами ежедневного спроса.
Из проведенного исследования видно, что для моделирования и прогнозирования спроса на группу товаров, выпускаемой предприятием, наиболее эффективно использовать методы математического моделирования.
1. Постановка задачи
Ранее нами была разработана следующая многокритериальная нечеткая математическая модель для проведения имитационного моделирования спроса на группу товаров выпускаемых предприятием (32):
XX с
а =1 1=1
XР Аг ^ таХ
/=1
п
£ 8 д ^ тт
/=1
т п
X XРгха < Ьа
а =1 >=1
Ъ, * О
(32)
Рг > №г
х га < д г , 1 = 1, х,а > 0, г = 1,
№ … №?]
— п, а = 1 , п, а = 1
, т , т
где Сг — коэффициент полезности цена г-го товара; рг — цена г-го товара;
х г — объем г-го товара, который купит потребитель;
Ьа — доход а-го потребителя;
дг — максимальный объем г-го товара;
^ — себестоимость г-го товара;
О — размер склада.
Рассмотрим более подробно такой параметр данной модели, как цена товара. Представим цену товара как функцию нескольких переменных, а именно:
р(2, Рг, К, Я, 1п)
где 2 — затраты на производство товара;
Рг — прогноз продаж товара (как правило, рассматривается три варианта прогноза — оптимистический, пессимистический и средний варианты);
К — показатель качества товара. Данный показатель может определяться при помощи методов экспертных оценок и приводиться к единой шкале;
Я — целевой уровень рентабельности;
1п — коэффициент инфляции.
Необходимо отметить, что затраты на производство товара также можно представить в виде функции многих переменных.
1=1
2(01, Q2, …, 0) ^ тт
1.1. Метод наискорейшего спуска
Проведем более детальное исследование функции затрат, как функции многих переменных.
Можно утверждать, что данная функция является монотонной для каждой переменной и имеющей разрывы на координатных плоскостях. Для минимизации данной функции можно использовать численные методы, а именно метод наискорейшего спуска. Данный метод описан в [3-7].
Направление наискорейшего спуска задается антиградиентом УГ (33):
х[“+1] = х{и ]-1[“]У^ (х[и ]) (33)
Iм выбирается:
— постоянной, тогда метод может расходиться;
— при помощи дробного шага, т.е. длина шага при спуске делится на заданное число;
— наискорейшим спуском (34):
Iм = а^тшя Р(Xм -Л[и]УР(Xм)) (34)
Алгоритм данного метода показан на рис. 4.
Рис. 4. Алгоритм метода наискорейшего спуска
1.2. Нейронные сети
Если для моделирования затрат как функции многих переменных достаточно использовать численные методы, то при представлении цены как функции многих переменных такой подход не применим. Поскольку цена является не только одним из важнейших факторов, который влияет на спрос но и одним из наиболее важным факторов при планировании прибыли предприятия.
Кроме того, в современной Российской экономике процесс ценообразования достаточно специфичен, и зачастую, не опирается на использование каких либо методов или стратегий ценообразования. При этом, как правило, назначается максимально возможная цена, что приводит к тому, что предприятие быстро теряет свою конкурентоспособность.
Следовательно, при проведении моделирования цены на конкретный товар, необходимо учитывать еще и специфику ценообразования на данном конкретном предприятии, для которого и проводится моделирование спроса.
Однако не какой из математических методов не дает такой возможности в полной мере. Поэтому принято решение для моделирования цены использовать методы искусственного интеллекта. Поскольку использование этих методов позволит наиболее четко и полно провести моделирование цены с учетов всех возможных факторов, влияющих на нее.
Из всех методов искусственного интеллекта наиболее оптимальными для проведения моделирования цены являются нейронные сети, которые позволяют принять решение, близкое к тому которое принял бы человек в той или иной конкретной ситуации.
Под нейронной сетью (нейросеть) будем понимать набор нейронов, которые определенным образом связанных между собой [8, 9].
Для решения поставленной задачи — моделирования цены на товар, выпускаемый предприятием, как функции многих переменных достаточно использовать трехслойный перцептрон с п входами и одним выходом.
Первый слой — вход, только передает входные сигналы ко всем Н нейронам второго слоя. Каждый нейрон второго слоя имеет п входов, у каждого из них есть весовые коэффициенты ^л, ^ц, …, ДЛЯ г -го нейрона. При получении входного сигнала нейрон суммирует их согласно весовым коэффициентам, после чего применяет к результату передаточную функцию и пересылает на вход одного и нейронов третьего слоя. После этого нейрон третьего слоя суммирует полученные со второго слоя результаты согласно весовым коэффициентам у,. Предположим, что передаточные функции в скрытом слое являются сигмоидными, а в выходном слое используется функция р(х) = х, т.е. взвешенная сумма выходов второго слоя и будет ответом нейросети [8].
Тогда, при подаче на входы перцептрона любых чисел х1, х2, …, хп, получаем на выходе значение некоторой функции ^(х1, х2, …, хп), которое
является ответом (реакцией) нейросети. Ответ нейросети при этом зависит как от входного сигнала, так и от значений ее внутренних параметров — весовых коэффициентов нейронов [8].
Пример такой нейросети показан на рис. 5.
Х1
Х3
Рис. 5. Пример трехслойной нейронной сети
Представление функции множества переменных при помощи нейронных сетей базируется на теореме Колмогорова, описанной в [8].
Любая непрерывная функция от п переменных Р(х, х2, …, хп) может быть представлена при помощи операций сложения, умножения и суперпозиции из непрерывных функций одной переменной [8].
2 п+1 п
х2,…,хп) = (X Ну )) (35)
]=1 >=1
где gj и Ну — непрерывные функции, при этом Ну не зависит от начальной функции Р.
Однако на практике данную теорему применить достаточно сложно, т.к. функции Ну вычисляются с трудом и не являются гладкими. Кроме того не очень понятно как подбирать коэффициенты gj для заданной функции Е
Для достижения более значимых результатов необходимо провести ослабление требований а именно:
— вместо точного соответствия функций использовать приближенное;
— можно увеличить число нейронов в скрытом слое нейросети.
Новый вариант теоремы Колмогорова, который учитывает приведенные выше требования, описан в [8].
Пусть Р(х1, х2, …, хп) — любая непрерывная функция, тогда существует такое число Н и наборы чисел Vу, щ и V , что функция:
н
/ (xl, х2,…,хп ) =Х VP(WІ1 х1 + х2 + … + ™пхп + Щ ) (36)
1=1
приближает данную функцию с погрешностью не более е на всей области определения[8].
Формула (36) полностью идентична функции, которая реализуется перцептроном нейронной трехслойной сети и описана в [10].
2. Мелкозернистые вычисления в однородных средах
После введения цены как функции многих переменных в разработанную автором математическую модель (32) невозможно ее итерационное последовательное решение, предложенное ранее.
Данную задачу можно решить только при помощи применения методов параллельного вычисления, а именно мелкозернистых вычислений, так как именно для них используются модели нейронных сетей. Под мелкозернистыми вычислениями будем понимать большое количество относительно простых вычислительных задач.
В нашем случае можно говорить о параллельном решении следующих задач:
1. минимизация затрат при помощи численных методов, а именно метода наискорейшего спуска;
2. определение цены на товар как функции многих переменных;
3. минимизация себестоимости;
4. максимизация прибыли;
5. моделирование спроса.
Как можно заметить, из предыдущего описания задачи приведены в укрупненном виде, и каждая из них состоит из большого количества мелких подзадач.
Если рассмотреть данные задачи с точки зрения классификации вычислительных задач, то они представляют собой потоки. Следовательно, можно говорить о том, что данный подход рациональней применять в однородных вычислительных средах.
Однородные вычислительные среды являются развитием однородных вычислительных систем. Под однородной вычислительной системой будем понимать такую систему, в которой почти все простые задачи примерно одинаковы по объему вычислений и связаны между собой одинаковыми схемами обмена. Т.е. система для решения сложной задачи может быть построена при помощи неких стандартных одинаковых блоков.
Кроме того в однородной вычислительной системе соблюдаются принципы параллельности задач и переменности логической структуры.
Вычислительные среды представляют собой многомерную решетчатую структуру.
** *
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
В работе рассмотрены вопросы использования методов мелкозернистых вычислений в однородных вычислительных средах при моделировании спроса на группу товаров, выпускаемых предприятием. В математической модели используются методы искусственного интеллекта, а именно: как нейронные сети, так и численные методы — метод наискорейшего спуска.
Список литературы:
1. Блауберг И.В., Юдин Э.Г. Становление и сущность системного подхода. — М.: Наука, 1973. — 269 с.
2. Волков Е.А. Численные методы. — М.: Наука, 1982. — 254 с.
3. Ермаков С.М. Методы Монте-Карло и смежные вопросы. — М.: Наука, 1971. — 471 с.
4. Самарский A.A., Гулин A.B. Численные методы. — М.: Наука, 1989. -430 с.
5. ТурчакЛ.И. Основычисленныхметодов. — М.: Наука, 1987. — 318 с.
6. Steven C.C., Raymond С. Numerical Methods for Engineers: With Software and Programming Applications. — McGraw-Hill Science / Engineering / Math, 2001. — 944 p.
7. Hamming R.W. Numerical Methods for Scientists and Engineers. — Dover Publications, 1987. — 721 p.
8. Струнков Т. Думал ли Гильберт о нейронных сетях? // PC Week RE. -1999. — № 13.
9. Хайкин С. Нейронные сети: полный курс. — М.: Вильямс, 2006. — 1104 с.
10. Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. — М.: Горячая линия — Телеком, 2001. — 382 с.
11. Корнеев В. Будущее высокопроизводительных вычислительных систем // Открытые системы. — 2003. — № 5.
12. Малышкин В.Э. Введение в параллельное программирование мультикомпьютеров. — Новосибирск: ИВМ и МГ СО РАН, 2003. — 268 с.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Спрос в математическом смысле понимается как зависимость между ценой (P) и количеством товара (Q), который покупатели могут и желают приобрести по определенной цене, в определенный промежуток времени.
Спрос с точки зрения экономики это есть платежеспособная надобность покупателей в этом товаре при данной цене. Спрос характеризуется величиной спроса – количеством товаров, которое покупатели готовы приобрести по данной цене. Его величина показывает, что покупатели готовы купить такое количество товаров, но это не значит, что сделки действительно состоятся т.к. это зависит от ряда экономических факторов. Например, производители могут оказаться не в состоянии выпустить подобное количество товара. Под словом «готовы» понимается то, что у них есть потребность и наличие необходимых денежных средств для покупки товара в данном количестве. Можно рассмотреть как спрос конкретного покупателя, так и спрос всех покупателей, присутствующих на рынке. В экономике изучается общая величина спроса, так как конкретного покупателя зависит от личных предпочтений покупателя и не отражает действительной картины, сложившейся на рынке. Например, конкретный покупатель может не испытывать нужды в каком-либо товаре (например, самокате) но, на рынке спрос на этот товар будет существовать. Как правило, спрос на товар подчиняется закону спроса.
Прогнозирование спроса – это предсказание развития рынка во времени на основе изучения причинно-следственных связей, тенденций и закономерностей.
Прогнозирование спроса исполнять роль научно доказанного предвидение формирования платежеспособных потребностей населения на товары и услуги. При прогнозировании микроспроса распространенными являются следующие методы: с использованием структурных моделей; с использованием коэффициента эластичности спроса; экономико-математические.
Экономико-математические методы предлагают применение авторегрессионных, трендовых и факторных моделей.
Трендовые модели употребляются только если спрос является функцией времени: Y=f(t), где t — фактор времени; Y — фактор времени- показатель спроса. Эта зависимость описывает динамическое развитие спроса во времени. Формы зависимости спроса от времени могут быть различными. Существуют несколько видов прогнозирования спроса в экономике при помощи математического моделирования
Так же существуют следующие виды прогнозирования в зависимости от временного периода: оперативное (до 1 месяца); краткосрочное (от 1 до 2 лет); среднесрочное (от 2 до 5 лет); долгосрочное (от5до10лет).
Прямолинейная форма связи имеет вид: где Y — показатель спроса; t — время; а0 а1-параметры уравнения. Для определения параметров уравнения ад и а, в данном случае нужно решить следующую систему уравнений:
na0+a1∑lgt= ∑ya0∑lgt+a1∑(lg)2=∑ylgt
Применение данной модели предполагает снижение в динамическом ряду как абсолютных, так и относительных приростов спроса. Показательная форма связи имеет вид: . Для нахождения параметров уравнения а0 и а1 нужно решить следующую систему уравнений:
na0+a1∑t=∑ya0∑t+a1∑t2=∑yt
Использование предоставленной модели полагает приблизительно одинаковые показатели абсолютных приростов в динамическом ряду при снижении относительных темпов прироста.
Логарифмическая форма связи имеет вид: . Для определения параметров уравнения а0 и а1 нужно решить следующую систему уравнений:
nlga0+lga1∑t=∑lgylga0∑t+lga1∑t2=∑lgy∙t
Применение данной модели предполагает примерно постоянные относительные темпы прироста показателей спроса в динамическом ряду. Параболическая форма связи имеет вид: . Для определения параметров уравнения а0, а1, а2 нужно решить следующую систему уравнений:
na0+a1∑t+a2∑t2=∑ya0∑t+a1∑t2+a2∑t3=∑yta0∑t2+a1∑t3+a2∑t4=∑yt2
Необходимо оценить модель, рассчитав среднюю ошибку аппроксимации: ,
где E- ошибка аппроксимации; yi– теоретические показатели ряда динамики, рассчитанные по модели; уi – эмпирические показатели ряда динамики; n – количество показателей в динамическом ряду.
Прогноз на основе рассчитанной модели может иметь смысл, если отклонение теоретических значений показателей спроса (Y) от эмпирических (Y) в каждом конкретном случае не будет составлять больше 3-5%, при этом средний процент отклонений также не должен быть больше 3-5%.
Если отклонения и ошибка аппроксимации будут находиться в пределах нормы, то это значит, что предоставленную модель можно применять для прогнозирования. Для этого надо задать значение t для прогнозируемого периода и, подставив это значение в уравнение, рассчитать показатель Y для прогнозируемого периода.
Факторные экономико-математические модели полагают, что спрос является функцией нескольких факторов. В виде факторов могут быть цены, совокупный объем спроса, объем реализации заменяемого товара и др. Y=f(x), где Y – показатель спроса; х — фактор.
Зависимость характеризует изменение развития спроса в связи с динамикой выбранных факторов. В практике существуют разнообразные формы зависимости. Методика использования факторных моделей подобна рассмотренной методике трендовых моделей, только в качестве фактора берется не время (t), а другой показатель (х). Используются различные формы криволинейной зависимости (параболы, гиперболы, логарифмические и др.).
Разновидностью экономико-математических методов при прогнозировании спроса является авторегрессионная модель, которая имеет вид: , где Y –показатель спроса отчетного периода; Yi-1 – показатель спроса за предшествующий период.
Зависимость характеризует связь показателей отчетного периода с предыдущим. Форма связи имеет вид:, где Y — показатель спроса в отчетном периоде; Yt-1 – показатель спроса в предшествующем периоде; а0, а1 – параметры уравнения.
Для определения параметров уравнения а0 и а1 нужно решить следующую систему уравнений:
nlga0+a1∑yt-1=∑yta0∑yt-1+a1∑yt-12=∑yt∙yt-1
Для целей прогнозирования нам также необходимо оценить данную модель с точки зрения соответствия теоретических значений эмпирическим. Сложность использования для прогнозирования спроса разобранных моделей состоит в том, что довольно тяжело получить оперативную и статистическую информацию о реализации, как отдельных товаров, так и отдельных товарных групп на предприятиях торговли. Модель может быть применена при прогнозировании, если среднее значение отклонений будет равное не больше 3 — 5%. В настоящее время отсутствует официальная статистическая отчетность о реализации по товарным группам. Однако предприятия торговли и общественного питания, имея современные средства обработки предоставляемых данных, такой информацией располагают, а, значит, могут вводить, разрабатывать и использовать соответствующие программы для прогноза реализации как в целом по отдельным группам товаров, так и по предприятию и даже отдельным товарам. Способность спроса повышаться или понижаться под влиянием воздействия различных факторов называется эластичностью спроса. Наиболее легким и приемлемым методом прогнозирования спроса для оперативных и краткосрочных целей является использование коэффициента эластичности.
Для количественного измерения воздействия какого-либо фактора на спрос применяют коэффициент эластичности. Коэффициент эластичности спроса – это показатель, характеризующий сравнительное изменение спроса под воздействием изменения фактора. Коэффициент эластичности можно рассчитать по формуле: ,
где Кэл – коэффициент эластичности; – изменение спроса в отчетном периоде по сравнению с базисным; х – показатель фактора в базисном периоде; – изменение фактора в отчетном периоде по сравнению с базисным; у – показатель спроса в базисном периоде.
При прогнозировании спроса как фактора могут выступать спрос, цены в целом по предприятию, спрос на другой товар, на уровне региона — доходы на душу населения. Коэффициент эластичности показывает, на сколько процентов изменится спрос (Y) при изменении фактора (Х) на 1 процент. При расчете коэффициента эластичности изменение спроса (–) и выбранного фактора () должно быть проанализировано не менее чем за 2-3 периода в ряду динамики. Показатели Y и X могут быть выражены как в относительных, так и в абсолютных показателях. Если показатели Y и X в базисном периоде равны 100%, то формула коэффициента эластичности будет иметь следующий вид:.Рассчитанный коэффициент эластичности может быть использован для краткосрочного прогнозирования если известно, на сколько изменится фактор в прогнозируемом периоде., где ∆Yпр – изменение спроса в прогнозируемом периоде; ∆x – изменение фактора в прогнозируемом периоде; Кэл – коэффициент эластичности между спросом и выбранным фактором. По этой формуле можно рассчитать, на сколько процентов изменится последнее значение в ряду динамики и спрос в прогнозируемом периоде. После чего можно установить объем спроса в прогнозируемом периоде:
, где Рn– объем спроса в прогнозируемом периоде; Рn-1 – объем спроса в последнем периоде до прогноза.
Рассмотрим пример применения математического моделирования при прогнозировании спроса.
Имеется динамический ряд показателей.
Периоды
Общий объем реализованного спроса по предприятию (Х), цепной темп роста, %
Спрос на группу А(Y), цепной темп роста, %
I вариант
II вариант
I вариант
II вариант
Базисный
99,0
99,0
99,0
99,0
Предшествующий
103,0
103,0
104,0
102,0
Отчетный
106,0
106,0
108,0
105,0
Для I варианта =[(108-99)/100]/[(106-99)/100]=1,29, или =[(108-99)/(106-99)]=9/7=1,29.
Это значит, что при повышении совокупного объема спроса по предприятию на 1 % спрос на группу А растет на 1,29%, то есть быстрее, чем общий объем реализованного спроса. Для II варианта =[(105-99)/100]/[(106-99)/100]=0,86, или =[(105-99)/(106-99)]=6/7=0,86.
Это означает, что при увеличении общего объема реализованного спроса в целом по предприятию на 1% спрос на группу А растет на 0,86%, т.е. медленнее, чем общий объем реализованного спроса. По имеющимся прогнозам, в планируемом периоде общий объем реализованного спроса по предприятию увеличится на 3%. Тогда спрос на группу А в планируемом периоде возрастет: в 1 варианте — на 3,87% (); во 2 варианте — на 2,58% (). Если учесть, что в отчетном периоде объем реализации по группе А составил 1500 руб., в прогнозируемом периоде возможный объем спроса по данной группе может составить: в 1 варианте – 1558 руб. =1500*1,0387; во 2 варианте — 1519 руб. =1500*1,0258.
При прогнозировании спроса могут быть применены и структурные модели, образованные на данных бюджетной статистики. В корне разработки таких моделей находятся данные опросов потребителей, при этом потребности группируются по выбранным признакам. Структурная модель имеет вид: ,
где Y — показатель спроса; Аi— предпочтительный набор потребностей в i-й группе; Si — число потребителей в i-й группе; n — число групп потребителей. Допустим, что произведена первичная группировка потребителей по уровню среднего дохода на душу населения. Все опрошенные были распределены на 4 группы. Затем на основании опроса определяется спрос на какой-либо товар внутри каждой группы, либо предпочтение одного товара другим. Полученные данные применяются в формуле структурной модели.
Кроме рассмотренных нами методов могут применяться и другие, например экономико-статистические. В условиях рыночных отношений прогнозирование и изучение спроса на товары и услуги является необходимым условием благополучного функционирования предприятий торговли, общественного питания и сферы услуг.
Список литературы
-
А.И. Орлов Эконометрика — М.: Экзамен, 2002. — 576 с.
-
Долгополова А.Ф. Моделирование стратегии управления в социально-экономических системах с использованием Марковских процессов/А.Ф. Долгополова// Вестник АПК Ставрополья.-2011. -№ 1. -С. 67-70.
-
Камбарова Е.С., Долгополова А.Ф. Эконометрические методы для исследования экономических явлений // Современные наукоемкие технологии. -2013. -№ 6. -С. 69-72.