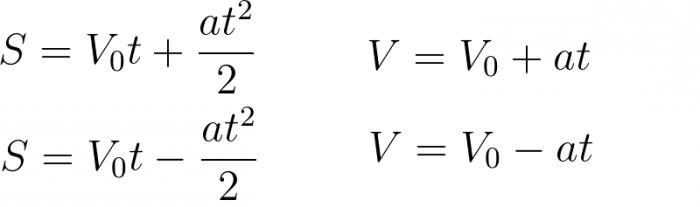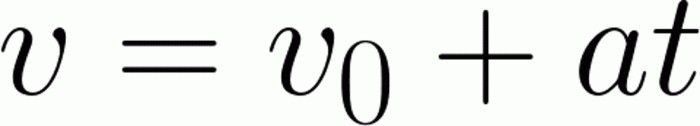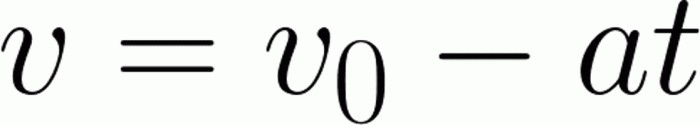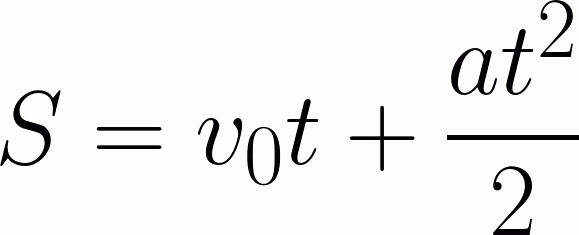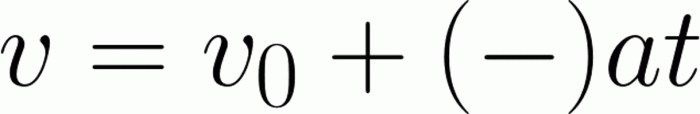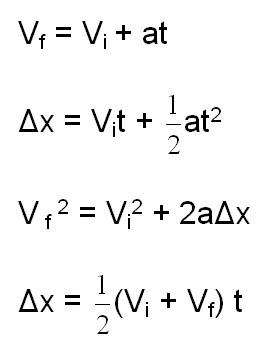Как найти материальную точку в физике

Что такое материальная точка? Какие физические величины связаны с ней, для чего вообще вводится понятие материальной точки? В этой статье мы порассуждаем об этих вопросах, приведем примеры задач, которые связаны с обсуждаемым понятием, а также поговорим о формулах, применяемых для их решения.

Определение

Итак, что же такое материальная точка? Разные источники дают определение в несколько разном литературном стиле. То же самое касается и преподавателей в вузах, колледжах и общеобразовательных учреждениях. Однако, согласно стандарту, материальной точкой называется тело, размерами которого (в сравнении с размерами системы отсчета) можно пренебречь.

Связь с реальными объектами

Казалось бы, как можно принять за материальную точку человека, велосипедиста, автомобиль, корабль и даже самолет, о которых в большинстве случаев идет речь в задачах по физике, когда речь заходит о механике движущегося тела? Давайте смотреть глубже! Для определения координаты движущегося тела в любой момент времени необходимо знать несколько параметров. Это и начальная координата, и скорость движения, и ускорение (если оно, конечно же, имеет место), и время.

Что необходимо для решения задач с материальными точками?

Координатную связь можно найти, только привязавшись к системе координат. Вот такой своеобразной системой координат для автомобиля и другого тела становится наша планета. А в сравнении с ее величиной размерами тела действительно можно пренебречь. Соответственно, если тело мы принимаем за материальную точку, ее координату в двухмерном (трехмерном) пространстве можно и нужно находить как координату геометрической точки.

Движение материальной точки. Задачи

В зависимости от сложности, задачи могут приобретать определенные условия. Соответственно, отталкиваясь от данных нам условий, можно использовать определенные формулы. Иногда, даже имея весь арсенал формул, решить задачу, что называется, «в лоб» все равно не представляется возможным. Поэтому крайне важно не просто знать формулы кинематики, имеющие отношение к материальной точке, но и уметь их использовать. То есть выражать нужную величину, а системы уравнений приравнивать. Вот основные формулы, которые мы будем применять в ходе решения задач:

Задача № 1

Автомобиль, стоящий на стартовой черте, резко начинает движение из неподвижного положения. Узнать, за какое время он разгонится до 20 метров в секунду, если его ускорение составляет 2 метра на секунду в квадрате.

Сразу хочется сказать, что эта задача – практически самое простое, что может ожидать ученика. Слово “практически” стоит здесь не просто так. Все дело в том, что проще может быть только подставить прямые значения в формулы. Нам же следует сначала выразить время, а затем произвести расчеты. Для решения задачи понадобится формула определения мгновенной скорости (мгновенная скорость — это скорость тела в определенный момент времени). Она имеет следующий вид:

Как мы видим, в левой части уравнения у нас стоит мгновенная скорость. Она нам там абсолютно не нужна. Поэтому делаем простые математические действия: произведение ускорения на время оставляем в правой части, а начальную скорость переносим влево. При этом следует внимательно следить за знаками, поскольку один неправильно оставленный знак может в корне изменить ответ к задаче. Далее немного усложняем выражение, избавляясь от ускорения в правой части: делим на него. В итоге справа у нас должно остаться чистое время, слева — двухуровневое выражение. Все это дело просто меняем местами, чтобы смотрелось привычнее. Остается только подставить величины. Итак, получается, что автомобиль разгонится за 10 секунд. Важно: мы решили задачу, предполагая, что в автомобиль в ней – материальная точка.

Задача № 2

Материальная точка начинает экстренное торможение. Определить, какой была начальная скорость в момент экстренного торможения, если до полной остановки тела прошло 15 секунд. Ускорение принять равным 2 метрам на секунду в квадрате.

Задача, в принципе, достаточно похожа на предыдущую. Но здесь есть пара своих нюансов. Во-первых, нам нужно определить скорость, которую мы обычно называем начальной. То есть в определенный момент начинается отсчет времени и расстояния, пройденного телом. Скорость при этом действительно будет подпадать под данное определение. Второй нюанс – знак ускорения. Напомним, что ускорение — это величина векторная. Следовательно, в зависимости от направления она будет изменять свой знак. Положительное ускорение наблюдается в том случае, если направление скорости тела совпадает с его направлением. Проще говоря, когда тело ускоряется. В противном случае (то есть в нашей ситуации с торможением) ускорение будет отрицательным. И эти два фактора нужно учитывать, чтобы решить данную задачу:

Как и в прошлый раз, сначала выразим необходимую нам величину. Чтобы избежать возни со знаками, начальную скорость оставим там, где она есть. С противоположным знаком переносим в другую часть уравнения произведение ускорения на время. Так как торможение было полным, конечная скорость составляет 0 метров в секунду. Подставляя эти и другие значения, легко находим начальную скорость. Она будет равна 30 метрам в секунду. Легко заметить, что, зная формулы, справляться с простейшими задачами не так уж и сложно.

Задача № 3

В определенный момент времени диспетчеры начинают слежение за перемещением воздушного объекта. Его скорость в этот момент равняется 180 километрам в час. Через промежуток времени, равный 10 секундам, его скорость увеличивается до 360 километров в час. Определите расстояние, пройденное самолетом за время перелета, если время полета составило 2 часа.

На самом деле в широком понимании данная задача имеет множество нюансов. Например, разгон воздушного судна. Понятно, что по прямолинейной траектории наше тело двигаться бы не могло в принципе. То есть ему нужно взлететь, набрать скорость, а потом уже на определенной высоте какой-то отрезок расстояния двигаться прямолинейно. В расчет не берутся отклонения, а также замедление самолета при посадке. Но это не наше дело в данном случае. Поэтому мы будем решать задачу в рамках школьных знаний, общих сведений о кинематическом движении. Чтобы решить задачу, нам понадобится следующая формула:

Но вот тут нас ожидает загвоздка, о которой мы говорили ранее. Знать формулы недостаточно – их нужно уметь использовать. То есть выводить одну величину при помощи альтернативных формул, находить ее и подставлять. При просмотре начальных сведений, которые имеются в задаче, сразу становится понятно, что решить ее просто так не получится. Об ускорении ничего не сказано, зато есть информация о том, как изменилась скорость за определенный промежуток времени. Значит, ускорение мы можем найти самостоятельно. Берем формулу нахождения мгновенной скорости. Она имеет вид

Ускорение и время оставляем в одной части, а начальную скорость переносим в другую. Затем делением обеих частей на время освобождаем правую часть. Здесь сразу же можно подсчитать ускорение, подставив прямые данные. Но гораздо целесообразнее выражать и дальше. Полученную для ускорения формулу подставляем в основную. Там можно немного сократить переменные: в числителе время дано в квадрате, а в знаменателе – в первой степени. Поэтому от этого знаменателя можно избавиться. Ну а дальше – простая подстановка, поскольку больше выражать ничего не надо. Ответ должен получиться следующий: 440 километров. Ответ будет другим, если переводить величины в другую размерность.

Заключение

Итак, что же мы выяснили в ходе этой статьи?

1) Материальная точка — это тело, размерами которого по сравнению с размерами системы отсчета можно пренебречь.

2) Для решения задач, связанных с материальной точкой, есть несколько формул (приведены в статье).

3) Знак ускорения в этих формулах зависит от параметра движения тела (ускорение или торможение).

Содержание книги

Предыдующая страница

§1. Описание положения тела в пространстве

1.4 Материальная точка

Во многих кинематических задачах оказывается возможным пренебречь размерами самого тела. Еще раз рассмотрим автомобиль, движущийся из Минска в Брест. Расстояние между этими городами порядка 350 километров, размеры автомобиля — несколько метров, поэтому в такой ситуации при описании положения автомобиля можно не учитывать его размеры — если капот автомобиля находится в Бресте у нужного подъезда нужного дома, то можно считать, что и его багажник находится приблизительно там же. Таким образом, в данной задаче можно мысленно заменить автомобиль его моделью — телом, размеры которого пренебрежимо малы. Такая модель тела очень часто используется в физике и называется материальной точкой.

Материальная точка — это идеальная модель тела, размерами которого в данных условиях можно пренебречь.

Общим у геометрической и материальной точек является отсутствие собственных размеров. Материальную точку, по мере необходимости, можно «наделять» свойствами, которыми обладают реальные тела, например, массой, энергией, электрическим зарядом и так далее.

Одним из критериев применимости модели материальной точки является малость размеров тела по сравнению с расстоянием, на которое оно перемещается. Однако это условие не является абсолютно однозначным. Так, описывая движение Земли вокруг Солнца при расчете ее положения на орбите, размерами Земли можно пренебречь, считать ее материальной точкой. Однако, если нам необходимо рассчитать времена восхода и заката Солнца, модель материальной точки принципиально неприменима, так как это описание требует учета вращения Земли, учета ее размеров и формы.

Рассмотрим еще один пример. Спринтеры соревнуются на стометровой дистанции. Цель описания движения – выявить, кто из спортсменов пробегает дистанцию за меньшее время (задача чисто кинематическая). Можно ли в данной задаче считать бегуна материальной точкой? Его размеры значительно меньше дистанции забега, но достаточно ли они малы, чтобы ими можно было пренебречь? Ответ на эти вопросы зависит от требуемой точности описания. Так, на серьезных соревнованиях время измеряется с точностью 0.01 секунды, за это время бегун смещается на расстояние порядка 10 сантиметров (простая оценка, полученная исходя из средней скорости спринтера 10 м/с). Следовательно, погрешность, с которой определяется положением бегуна (10 см) меньше, чем его поперечные размеры, поэтому модель материальной точки в данном случае неприменима. Не случайно мастера спринтерского бега на финише «бросают грудь вперед», выигрывая драгоценные сотые доли секунды. Таким образом, вторым критерием применимости модели является требуемая точность описания физического явления.

В некоторых ситуациях можно использовать модель материальной точки, даже если размеры тела сравнимы и даже больше расстояний, на которое смещается тело. Это допустимо тогда, когда положение одной точки тела однозначно определяет положение всего тела. Так при скольжении бруска по наклонной плоскости, зная положение его центра (как, впрочем, и любой другой точки) можно найти положение всего тела. Если модель материальной точки оказывается неприменимой, то необходимо использовать другие более сложные модели.

Следующая страница

Эта абстрактная модель представляет собой идеальное тело, имеющее определённую массу, размеры которого не имеют значения и не принимаются во внимание.

Такое упрощение необходимо для более простого решения различных задач, связанных с механическим движением.

Физические основы механики

Физика — это наука о природе, изучающая наиболее простые и общие свойства, присущие материальному миру. Благодаря этому, она является универсальной базой для естествознания и техники, а также состоит из большого количества отдельных дисциплин — классической и квантовой механики, теории относительности, а также электродинамики, оптики и прочих.

Изучение физики начинается с механики — раздела, который рассматривает движение как изменение положения тела в пространстве с течением времени. Поэтому законы механики наиболее ясно выражают пространственно-временные отношения между объектами и событиями.

Основополагающие законы физики были в своё время установленны именно на основе наблюдения соответствующих явлений и экспериментов, из-за этого, за небольшим исключением, сфера их применения довольно ограничена. В частности, классическая механика распространяется лишь на медленное движение частиц и тел в макроскопических областях пространства. Перемещение на околосветовых скоростях подчиняется законам теории относительности, а свойствами микроскопических частиц занимается квантовая механика.

Классическая механика решает две основные задачи:

1. Установление законов движения — соотношений, позволяющих выяснить характер и показатели перемещения любого тела или системы в зависимости от его взаимодействия с другими объектами.
2. Нахождение таких общих соотношений между механическими характеристиками систем, не зависящими от их состава, строения и конкретного взаимодействия элементов.

Решение первой задачи в своё время привело Исаака Ньютона к открытию общих принципов движения материальной точки — динамики. Вторая послужила установлению законов о сохранении импульса и энергии.

Модели и относительность

Физика относится к точным наукам — свои результаты она выражает не только на словах, но и с помощью математических соотношений и формул. Однако свойства физических тел и явлений настолько многогранны, что даже самая совершенная теория не в состоянии отобразить их во всей своей полноте. Поэтому вместо реальных объектов, наука предпочитает оперировать физическими моделями — идеализированными телами, которые отображают лишь существенные для рассмотрения явлений свойства и факторы.

В механике существует две основные модели:

1. Материальной точкой может называться тело, размерами которого при решении конкретной задачи разрешается пренебречь.
2. Абсолютно твёрдым телом следует считать объект, взаимное расположение всех составляющих которого остаётся стабильным. Другими словами, это система, состоящая из жёстко связанных точек и не подверженная деформации.

Положение объекта в пространстве и его перемещение можно определить лишь относительно другого материального тела отсчёта и связанной с ним системой координат. Помимо этого, для описания движения необходимо пользоваться общепринятым и согласованным принципом фиксации моментов, а также иметь возможность проведения измерений временных промежутков во всех точках пространства.

Совокупность тела отсчёта, системы координат и неподвижного относительно неё хронометра называют системой отсчёта.

Таким образом, местоположение и перемещение любого объекта во вселенной может быть определено лишь относительно конкретной точки, от которой ведётся отсчёт. В то же время выбор системы отсчёта является произвольным и определяется лишь удобством для описания движения в заданных условиях. Отсюда следует, что положение объекта и его перемещение в пространстве является относительным по определению.

Понятие материальной точки

В отличие от геометрической точки, не имеющей никаких материальных свойств и обладающей лишь одной пространственной координатой, материальная может иметь массу, электрический заряд и прочие характеристики, необходимые для решения конкретной задачи.

Определение материальной точки в физике необходимо ввести для упрощения расчётов. Очевидно, что для описания движения такой абстрактной модели требуется минимальное количество вычислительных ресурсов.

Как правило, точке приписывается масса реального объекта, а остальные характеристики опускаются. Это можно делать лишь в том случае, когда перемещение, совершаемое наблюдаемым телом, несоизмеримо больше его размера. К примеру, для описания движения Земли по солнечной орбите совсем необязательно учитывать её вращение вокруг собственной оси.

Если возникла необходимость рассчитать среднюю скорость авиалайнера, следующего по определённому пути, форма его корпуса не имеет никакого значения. В таком случае самолёт являет собой пример материальной точки, которая должна пройти определённое расстояние за промежуток времени. Однако при нахождении показателя сопротивления воздуха летательный аппарат необходимо рассматривать как сложную систему.

При поступательном движении все элементы тела движутся в одном направлении, его можно принимать за точку

Несмотря на универсальность и удобство точечной модели, её применение имеет существенные ограничения. Это хорошо видно на примере разреженного газа при высокой температуре. Каждая молекула имеет очень маленький размер, несоизмеримый с путём, который она проходит в пространстве. Однако в этом случае молекулу далеко не всегда можно принять за точку. Дело в том, что колебание и вращение частиц перегретого газа создают своеобразный энергетический резервуар, и пренебрегать этими характеристиками в большинстве случаев нельзя.

Описание движения в кинематике

Кинематика — это начальный раздел механики, в котором устанавливаются понятия и величины, определяющие движение, общие соотношения между его характеристиками и способы описания. В разделе не рассматриваются условия и причины, определяющие характер движения тел. Поскольку любой предмет можно считать как систему идеальных моделей, прежде всего рассматривается кинематика одной точки.

Существует три способа описания движения и положения точки в выбранной системе отсчёта:

1. Векторный основан на понятии радиус-вектора и является наиболее удобным для теории, поскольку позволяет лаконично и полно отобразить содержание кинематических величин и связь между ними.
2. Координатный. С телом отсчёта жёстко связывается любая система координат, чаще всего декартова, а положение точек обозначается при помощи трёх числовых значений: x, y, z. Эти числа соответствуют расстоянию от начала координат до проекции точки на соответствующую координатную ось.
3. Природный способ отлично подходит для описания движения по заданной траектории. Положение точки задаётся криволинейной координатой, которая представляет собой расстояние от начала отсчёта до этой точки, отложенное вдоль траектории. Закон движения при этом определяется зависимостью координаты от времени.

В классической механике для удобства используются инерциальные системы отсчёта. Их особенность заключается в том, что движение всех тел происходит равномерно и прямолинейно или же полностью отсутствует. Пространство и время в такой системе обладают изотропным и равномерным строением.

Динамика и законы Ньютона

Динамика — это раздел механики, в котором законы движения тел устанавливаются через причины, обусловливающие его характер. Основу раздела составляют 3 закона Ньютона, являющиеся обобщением результатов наблюдений и специально поставленных экспериментов. Их не получится вывести из каких-либо более простых принципов.

Законы динамики имеют важное практическое значение. На них основаны расчёты, по которым сооружаются всевозможных машины и механизмы, инженерные конструкции, космические аппараты и прочая техника.

Однако стоит заметить, что утверждения Ньютона не являются универсальными даже в рамках классической механики и выполняются лишь в инерциальных системах отсчёта.

Три закона Ньютона:

1. Тело, находящееся в инерциальной системе отсчёта при условии отсутствия взаимодействия с другими объектами, будет находиться в покое или совершать прямолинейное и равномерное движение.
2. Сила, действующая на тело, полностью определяет скорость, с которой изменяется импульс этого тела.
3. Два тела действуют друг на друга с силами равными по модулю и направленными в противоположные стороны прямой, соединяющей эти тела.

Законы Ньютона нельзя изолировать друг от друга, так как они — система органичных и взаимосвязанных утверждений. Они применяются для решения любой задачи динамики, но второй закон принято считать основным, поскольку он непосредственно оперирует основными характеристиками движения.

Для определения законов движения точки необходимо иметь достоверную и полную информацию о силах, действующих на неё.

В макроскопическом мире можно наблюдать большое количество всевозможных сил, которые являются проявлениями двух самых фундаментальных взаимодействий во вселенной — электромагнитного и гравитационного. Притяжение обусловлено гравитацией, а все остальные известные науке силы имеют электромагнитную природу.

Кратко ознакомившись с особенностями классической механики, можно понять, с какой целью используется понятие материальной точки. Нужно понимать, что физика не работают с реальными объектами, а лишь с абстрактными моделями. Это помогает облегчить теоретические построения и расчёты.

Определение

Материальной точкой называется макроскопическое тело, размерами, формой, вращением и внутренней структурой которого можно пренебречь при описании его движения.