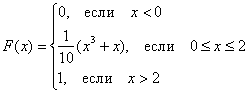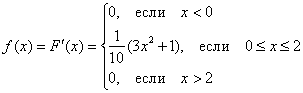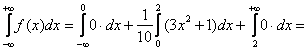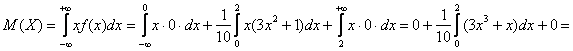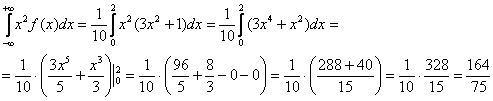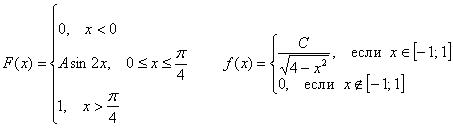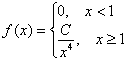Как найти матожидание функции случайной величины

Как найти математическое ожидание?

Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание — это первый начальный момент заданной СВ.

Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины — срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).

Нужна помощь? Решаем теорию вероятностей на отлично

Полезная страница? Сохрани или расскажи друзьям

Формула среднего случайной величины

Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$

Пример нахождения математического ожидания

Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.

Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$

Используем формулу для м.о. дискретной случайной величины:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Получаем:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Вот в этом примере 2 описано также нахождение дисперсии Х.

Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.

Используем для нахождения мат. ожидания формулу:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Подставляем из условия плотность вероятности и вычисляем значение интеграла:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{1} 12(x^2-x^3) cdot x dx = int_{0}^{1} 12(x^3-x^4) dx = \
=left.(3x^4-frac{12}{5}x^5) right|_0^1=3-frac{12}{5} = frac{3}{5}=0.6.
$$

Другие задачи с решениями по ТВ

Подробно решим ваши задачи по теории вероятностей

Вычисление математического ожидания онлайн

Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.

  • Введите число значений случайной величины К.
  • Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
  • Нажмите на кнопку «Вычислить».
  • Калькулятор покажет вычисленное математическое ожидание $M(X)$.

Видео. Полезные ссылки

Видеоролики: что такое среднее (математическое ожидание)

Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).

Лучшее спасибо — порекомендовать эту страницу

Полезные ссылки

А теперь узнайте о том, как находить дисперсию или проверьте онлайн-калькулятор для вычисления математического ожидания, дисперсии и среднего квадратического отклонения дискретной случайной величины.

Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по терверу. Для закрепления материала — еще примеры решений по теории вероятностей.

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

Источник

Функции случайных величин

Определение функции случайных величин. Функция дискретного случайного аргумента и ее числовые характеристики. Функция непрерывного случайного аргумента и ее числовые характеристики. Функции двух случайных аргументов. Определение функции распределения вероятностей и плотности для функции двух случайных аргументов.

Закон распределения вероятностей функции одной случайной величины

При решении задач, связанных с оценкой точности работы различных автоматических систем, точности производства отдельных элементов систем и др., часто приходится рассматривать функции одной или нескольких случайных величин. Такие функции также являются случайными величинами. Поэтому при решении задач необходимо знать законы распределения фигурирующих в задаче случайных величин. При этом обычно известны закон распределения системы случайных аргументов и функциональная зависимость.

Таким образом, возникает задача, которую можно сформулировать так.

Дана система случайных величин (X_1,X_2,ldots,X_n), закон распределения которой известен. Рассматривается некоторая случайная величина Y как функция данных случайных величин:

Y=varphi(X_1,X_2,ldots,X_n).

(6.1)

Требуется определить закон распределения случайной величины Y, зная вид функций (6.1) и закон совместного распределения ее аргументов.

Рассмотрим задачу о законе распределения функции одного случайного аргумента

Y=varphi(X).

Пусть X — дискретная случайная величина, имеющая ряд распределения

begin{array}{|c|c|c|c|c|}hline{X}&x_1&x_2&cdots&x_n\hline{P}&p_1&p_2&cdots&p_n\hlineend{array}

Тогда Y=varphi(X) также дискретная случайная величина с возможными значениями y_1=varphi(x_1),y_2=varphi(x_2),ldots,y_n=varphi(x_n). Если все значения y_1,y_2,ldots,y_n различны, то для каждого k=1,2,ldots,n события {X=x_k} и {Y=y_k=varphi(x_k)} тождественны. Следовательно,

P{Y=y_k}=P{X=x_k}=p_k

и искомый ряд распределения имеет вид

begin{array}{|c|c|c|c|c|}hline{Y}&y_1=varphi(x_1)&y_2=varphi(x_2)&cdots&y_n=varphi(x_n)\hline{P}&p_1&p_2&cdots&p_n\hlineend{array}

Если же среди чисел y_1=varphi(x_1),y_2=varphi(x_2),ldots,y_n=varphi(x_n) есть одинаковые, то каждой группе одинаковых значений y_k=varphi(x_k) нужно отвести в таблице один столбец и соответствующие вероятности сложить.

Для непрерывных случайных величин задача ставится так: зная плотность распределения f(x) случайной величины X, найти плотность распределения g(y) случайной величины Y=varphi(X). При решении поставленной задачи рассмотрим два случая.

Предположим сначала, что функция y=varphi(x) является монотонно возрастающей, непрерывной и дифференцируемой на интервале (a;b), на котором лежат все возможные значения величины X. Тогда обратная функция x=psi(y) существует, при этом являясь также монотонно возрастающей, непрерывной и дифференцируемой. В этом случае получаем

g(y)=fbigl(psi(y)bigr)cdot |psi'(y)|.

(6.2)

Пример 1. Случайная величина X распределена с плотностью

f(x)=frac{1}{sqrt{2pi}}e^{-x^2/2}

Найти закон распределения случайной величины Y, связанной с величиной X зависимостью Y=X^3.

Решение. Так как функция y=x^3 монотонна на промежутке (-infty;+infty), то можно применить формулу (6.2). Обратная функция по отношению к функции varphi(x)=x^3 есть psi(y)=sqrt[LARGE{LARGE{3}}]{y}, ее производная psi'(y)=frac{1}{3sqrt[LARGE{LARGE{3}}]{y^2}}. Следовательно,

g(y)=frac{1}{3sqrt{2pi}}e^{-sqrt[LARGE{LARGE{3}}]{y^2}/2}frac{1}{sqrt[LARGE{LARGE{3}}]{y^2}}

Рассмотрим случай немонотонной функции. Пусть функция y=varphi(x) такова, что обратная функция x=psi(y) неоднозначна, т. е. одному значению величины y соответствует несколько значений аргумента x, которые обозначим x_1=psi_1(y),x_2=psi_2(y),ldots,x_n=psi_n(y), где n — число участков, на которых функция y=varphi(x) изменяется монотонно. Тогда

g(y)=sumlimits_{k=1}^{n}fbigl(psi_k(y)bigr)cdot |psi'_k(y)|.

(6.3)

Пример 2. В условиях примера 1 найти распределение случайной величины Y=X^2.

Решение. Обратная функция x=psi(y) неоднозначна. Одному значению аргумента y соответствуют два значения функции x

begin{gathered}x_1=psi_1(y)=+sqrt{y};\x_2=psi_2(y)=-sqrt{y}.end{gathered}

Применяя формулу (6.3), получаем:

begin{gathered}g(y)=f(psi_1(y))|psi'_1(y)|+f(psi_2(y))|psi'_2(y)|=\\=frac{1}{sqrt{2pi}},e^{-left(-sqrt{y^2}right)^2/2}!left|-frac{1}{2sqrt{y}}right|+frac{1}{sqrt{2pi}},e^{-left(sqrt{y^2}right)^2/2}!left|frac{1}{2sqrt{y}}right|=frac{1}{sqrt{2pi{y}}},e^{-y/2}.end{gathered}

Закон распределения функции двух случайных величин

Пусть случайная величина Y является функцией двух случайных величин, образующих систему (X_1;X_2), т. е. Y=varphi(X_1;X_2). Задача состоит в том, чтобы по известному распределению системы (X_1;X_2) найти распределение случайной величины Y.

Пусть f(x_1;x_2) — плотность распределения системы случайных величин (X_1;X_2). Введем в рассмотрение новую величину Y_1, равную X_1, и рассмотрим систему уравнений

left{!begin{gathered}y=varphi(x_1;x_2);hfill\y_1=x_1.hfillend{gathered}right.

Будем полагать, что эта система однозначно разрешима относительно x_1,x_2

left{!begin{gathered}x_2=psi(y;y_2);hfill\x_1=y_1.hfillend{gathered}right.

и удовлетворяет условиям дифференцируемости.

Плотность распределения случайной величины Y

g_1(y)=intlimits_{-infty}^{+infty}f(x_1;psi(y;x_1))!left|frac{partialpsi(y;x_1)}{partial{y}}right|dx_1.

Заметим, что рассуждения не изменяются, если введенную новую величину Y_1 положить равной X_2.

Математическое ожидание функции случайных величин

На практике часто встречаются случаи, когда нет особой надобности полностью определять закон распределения функции случайных величин, а достаточно только указать его числовые характеристики. Таким образом, возникает задача определения числовых характеристик функций случайных величин помимо законов распределения этих функций.

Пусть случайная величина Y является функцией случайного аргумента X с заданным законом распределения

Y=varphi(X).

Требуется, не находя закона распределения величины Y, определить ее математическое ожидание

M(Y)=M[varphi(X)].

Пусть X — дискретная случайная величина, имеющая ряд распределения

begin{array}{|c|c|c|c|c|}hline{x_i}&x_1&x_2&cdots&x_n\hline{p_i}&p_1&p_2&cdots&p_n\hlineend{array}

Составим таблицу значений величины Y и вероятностей этих значений:

begin{array}{|c|c|c|c|c|}hline{y_i=varphi(x_i)}&y_1=varphi(x_1)&y_2=varphi(x_2)&cdots&y_n=varphi(x_n)\hline{p_i}&p_1&p_2&cdots&p_n\hlineend{array}

Эта таблица не является рядом распределения случайной величины Y, так как в общем случае некоторые из значений могут совпадать между собой и значения в верхней строке не обязательно идут в возрастающем порядке. Однако математическое ожидание случайной величины Y можно определить по формуле

M[varphi(X)]=sumlimits_{i=1}^{n}varphi(x_i)p_i,

(6.4)

так как величина, определяемая формулой (6.4), не может измениться от того, что под знаком суммы некоторые члены будут заранее объединены, а порядок членов изменен.

Формула (6.4) не содержит в явном виде закон распределения самой функции varphi(X), а содержит только закон распределения аргумента X. Таким образом, для определения математического ожидания функции Y=varphi(X) вовсе не требуется знать закон распределения функции varphi(X), а достаточно знать закон распределения аргумента X.

Для непрерывной случайной величины математическое ожидание вычисляется по формуле

M[varphi(X)]=intlimits_{-infty}^{+infty}varphi(x)f(x),dx,

где f(x) — плотность распределения вероятностей случайной величины X.

Рассмотрим случаи, когда для нахождения математического ожидания функции случайных аргументов не требуется знание даже законов распределения аргументов, а достаточно знать только некоторые их числовые характеристики. Сформулируем эти случаи в виде теорем.

Теорема 6.1. Математическое ожидание суммы как зависимых, так и независимых двух случайных величин равно сумме математических ожиданий этих величин:

M(X+Y)=M(X)+M(Y).

Теорема 6.2. Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс корреляционный момент:

M(XY)=M(X)M(Y)+mu_{xy}.

Следствие 6.1. Математическое ожидание произведения двух некоррелированных случайных величин равно произведению их математических ожиданий.

Следствие 6.2. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

Дисперсия функции случайных величин

По определению дисперсии имеем D[Y]=M[(Y-M(Y))^2].. Следовательно,

D[varphi(x)]=M[(varphi(x)-M(varphi(x)))^2], где M(varphi(x))=M[varphi(X)].

Приведем расчетные формулы только для случая непрерывных случайных аргументов. Для функции одного случайного аргумента Y=varphi(X) дисперсия выражается формулой

D[varphi(x)]=intlimits_{-infty}^{+infty}(varphi(x)-M(varphi(x)))^2f(x),dx,

(6.5)

где M(varphi(x))=M[varphi(X)] — математическое ожидание функции varphi(X); f(x) — плотность распределения величины X.

Формулу (6.5) можно заменить на следующую:

D[varphi(x)]=intlimits_{-infty}^{+infty}varphi^2(x)f(x),dx-M^2(X)

Рассмотрим теоремы о дисперсиях, которые играют важную роль в теории вероятностей и ее приложениях.

Теорема 6.3. Дисперсия суммы случайных величин равна сумме дисперсий этих величин плюс удвоенная сумма корреляционных моментов каждой из слагаемых величин со всеми последующими:

D!left[sumlimits_{i=1}^{n}X_iright]=sumlimits_{i=1}^{n}D[X_i]+2sumlimits_{i<j}mu_{x_ix_j}

Следствие 6.3. Дисперсия суммы некоррелированных случайных величин равна сумме дисперсий слагаемых:

D!left[sumlimits_{i=1}^{n}X_iright]=sumlimits_{i=1}^{n}D[X_i]

Теорема 6.4. Дисперсия произведения двух независимых случайных величин вычисляется по формуле

D[XY]=D[X]D[Y]+M^2(X)D[Y]+M^2(Y)D[X].

Корреляционный момент функций случайных величин

Согласно определению корреляционного момента двух случайных величин X и Y, имеем

mu_{xy}=M[(X-M(X))(Y-M(Y))].

Раскрывая скобки и применяя свойства математического ожидания, получаем

mu_{xy}=M(XY)-M(X)M(Y).

(6.6)

Рассмотрим две функции случайной величины X

Y_1=varphi_1(X);qquad Y_2=varphi_2(X).

Согласно формуле (6.6)

mu_{y_1y_2}= M(Y_1Y_2)-M(Y_1)M(Y_2).

отсюда

mu_{y_1y_2}=M(varphi_1(X)varphi_2(X))-M(varphi_1(X))M(varphi_2(X)).

т.е. корреляционный момент двух функций случайных величин равен математическому ожиданию произведения этих функций минус произведение из математических ожиданий.

Рассмотрим основные свойства корреляционного момента и коэффициента корреляции.

Свойство 1. От прибавления к случайным величинам постоянных величин корреляционный момент и коэффициент корреляции не изменяются.

Свойство 2. Для любых случайных величин X и Y абсолютная величина корреляционного момента не превосходит среднего геометрического дисперсий данных величин:

|mu_{xy}|leqslantsqrt{D[X]cdot D[Y]}=sigma_xcdot sigma_y,

где sigma_x,sigma_y — средние квадратические отклонения величин X и Y.

Следствие 6.5. Для любых случайных величин X и Y абсолютная величина коэффициента корреляции не превосходит единицы:

|r_{xy}|leqslant1.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Рассмотрим случайную
функцию Х(t).
При фиксированном значении аргумента,
например при t=t1,
получим
сечение—случайную величину Х(t1)
с математическим ожиданием М[X(t1)].
(Полагаем, что математическое ожидание
любого сечения существует.) Таким
образом, каждое фиксированное значение
аргумента определяет сечение—случайную
величину, а каждой случайной величине
соответствует ее математическое
ожидание. Отсюда следует, что каждому
фиксированному значению аргумента t
соответствует определенное математическое
ожидание; это означает, что математическое
ожидание случайной функции есть функция
(неслучайная) от аргумента t;
ее обозначают через mx(t).
В частном случае функция тx(t)
может сохранять постоянное значение
при всех допустимых значениях аргумента.
Дадим теперь определение математического
ожидания.

Математическим
ожиданием случайной функции Х(t)
называют
неслучайную функцию mx(t),
значение которой при каждом фиксированном
значении аргумента t
равно математическому ожиданию сечения,
соответствующего этому же фиксированному
значению аргумента:

mx(t)=M[X(t)].

Геометрически
математическое ожидание случайной
функции можно истолковать как «среднюю
кривую», около которой расположены
другие кривые—реализации; при
фиксированном значении аргумента
математическое ожидание есть среднее
значение сечения («средняя ордината»),
вокруг которого расположены его возможные
значения (ординаты).

§ 5. Свойства математического ожидания случайной функции

Используя свойства
математического ожидания случайной
величины, легко получить свойства
математического ожидания случайной
функции.

Свойство
1.
Математическое
ожидание неслучайной функции
φ(t)(О
равно
самой неслучайной функции:

М[φ(t)]=φ(t).

Свойство
2.
Неслучайный
множитель
φ(t)
можно выносить за знак математического
ожидания:

М[φ(t)Х(t)]=φ(t)М[X(t)]=φ(t)тx(t).

Свойство
3.
Математическое
ожидание суммы двух случайных функций
равно сумме математических ожиданий
слагаемых:

M[X(t)+Y(t)]=mx(t)+my(t).

Следствие.
Для
того чтобы найти математическое ожидание
суммы случайной и неслучайной функций,
достаточно к математическому ожиданию
случайной функции прибавить неслучайную
функцию:

M[X(t)+φ(t)]=mx(t)+φ(t).

Рекомендуем
самостоятельно доказать приведенные
свойства, учитывая, что при любом
фиксированном значении аргумента
случайная функция является случайной
величиной, а неслучайная функция—постоянной
величиной. Например, свойство 3 доказывается
так: при фиксированном значении аргумента
случайные функции Х(t)
и У(t)
являются случайными величинами, для
которых математическое ожидание суммы
равно сумме математических ожиданий
слагаемых.

Пример.
Найти математическое ожидание случайной
функции X(t)=Ucost,
где U—случайная
величина, причем M(U)=2.

Решение. Найдем
математическое ожидание, учитывая, что
неслучайный множитель cost
можно вынести за знак математического
ожидания:

М[X(t)]=М
[Ucos
t]
=
cos tM(U)
=
2 cost.

Итак, искомое
математическое ожидание mx(t)=3cost.

§ 6, Дисперсия случайной функции

Рассмотрим случайную
функцию Х(t).
При фиксированном значении аргумента,
например при t=t1,
получим
сечение—случайную величину Х(t1)
с дисперсией D[X(t1)]=0
(предполагается, что дисперсия любого
сечения существует). Таким образом,
каждое фиксированное значение аргумента
определяет сечение—случайную величину,
а каждой случайной величине соответствует
ее дисперсия. Отсюда следует, что каждому
фиксированному значению аргумента t
соответствует определенная дисперсия;
это означает, что дисперсия случайной
функции есть функция (неслучайная,
причем неотрицательная) от аргумента
t;
ее обозначают через Dx(t).
В частном случае Dx(t)
может сохранять постоянное значение
при всех допустимых значениях аргумента.
Дадим теперь определение дисперсии.

Дисперсией
случайной функции Х(t)
называют неслучайную неотрицательную
функцию Dx(t),
значение которой при каждом фиксированном
значении аргумента t
равно дисперсии сечения, соответствующего
этому же фиксированному значению
аргумента:

Dx(t)=D[X(t)].

Дисперсия
характеризует степень рассеяния
возможных реализации (кривых) вокруг
математического ожидания случайной
функции («средней кривой»). При
фиксированном значении аргумента
дисперсия характеризует степень
рассеяния возможных значений (ординат)
сечения вокруг математического ожидания
сечения («средней ординаты»).

Часто вместо
дисперсии рассматривают среднее
квадратическое отклонение случайной
функции, которое определяют по аналогии
со средним квадратическим отклонением
случайной величины.

Средним
квадратическим отклонением случайной
функции
называют квадратный корень из дисперсии:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Непрерывная случайная величина

  • Краткая теория
  • Примеры решения задач
  • Задачи контрольных и самостоятельных работ

Краткая теория

Случайная величина называется непрерывной, если ее функция
распределения

 непрерывно дифференцируема. В этом случае

 имеет производную, которую обозначим через

 – плотность распределения вероятностей.

Плотностью распределения вероятностей непрерывной случайной
величины

 называются функцию

 – первую производную от функции распределения

:

Из этого определения следует, что функция распределения является
первообразной для плотности распределения.

Заметим, что для описания распределения вероятностей дискретной
случайной величины плотность распределения неприменима.

Вероятность того, что непрерывная случайная величина

 примет значение, принадлежащее интервалу

 равна определенному интегралу от плотности
распределения, взятому в пределах от

 до

.

Зная плотность распределения

,
можно найти функцию распределения

 по формуле:

Числовые характеристики непрерывной случайной величины

Математическое ожидание непрерывной случайной величины

,
возможные значения которой принадлежат всей оси

,
определяется равенством:

где

 – плотность распределения случайной величины

.
Предполагается, что интеграл сходится абсолютно.

В частности, если все возможные значения принадлежат интервалу

,
то:

Все свойства математического ожидания, указанные для
дискретных случайных величин, сохраняются и для непрерывных величин.

Дисперсия непрерывной случайной величины

,
возможные значения которой принадлежат всей оси

,
определяется равенством:

или равносильным равенством:

В частности, если все возможные значения

 принадлежат интервалу

,
то

или

Все свойства дисперсии, указанные для дискретных случайных
величин, сохраняются и для непрерывных случайных величин.

Среднее квадратическое отклонение
непрерывной случайной величины определяется так же, как и для дискретной
величины:

При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.

Основные законы распределения непрерывных случайных величин

  • Нормальный закон распределения СВ
  • Показательный закон распределения СВ
  • Равномерный закон распределения СВ

Примеры решения задач

Пример 1

Дана
функция распределения F(х) непрерывной случайной величины 
Х.

Найти плотность распределения вероятностей f(x), математическое ожидание M(X), дисперсию D(X) и вероятность попадания X на отрезок [a,b]. Построить графики функций F(x) и f(x).

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Плотность
распределения вероятностей:

Математическое
ожидание:

Дисперсию
можно найти по формуле:

Вероятность
попадания на отрезок:

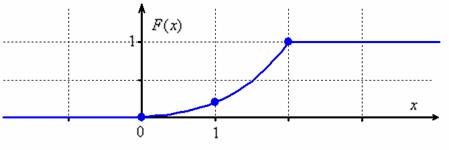
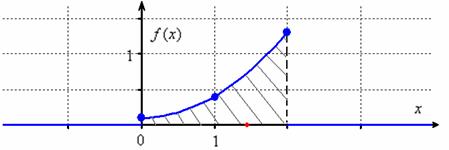
Построим графики функций F(x) и f(x).

График плотности
распределения

График функции
распределения

Пример 2

Случайная величина Х задана плотностью вероятности

Определить константу c, математическое ожидание, дисперсию, функцию распределения величины X, а также вероятность ее попадания в интервал [0;0,25].

Решение

Константу

 определим,
используя свойство плотности вероятности:

В нашем случае:

Найдем математическое
ожидание:

Найдем дисперсию:

Искомая дисперсия:

Найдем функцию
распределения:

для

:

для

:

для

:

Искомая функция
распределения: 

Вероятность попадания
в интервал

:

Пример 3

Плотность
распределения непрерывной случайной величины

 имеет вид:

Найти:

а)
параметр

;

б)
функцию распределения

;

в)
вероятность попадания случайной величины

 в интервал

г)
математическое ожидание

 и дисперсию

д)
построить графики функций

 и

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

а)
Постоянный параметр

 найдем из
свойства плотности вероятности:

В нашем
случае эта формула имеет вид:

б)
Функцию распределения

 найдем из
формулы:

Учитывая
свойства

,  сразу можем отметить,
что:

Остается
найти выражение для

, когда

 принадлежит
интервалу

:

Получаем:  

в)
Вероятность
попадания случайной величины

 в интервал

:

г)
Математическое ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

Среднее
квадратическое отклонение равно квадратному корню из дисперсии:

д) Построим графики

 и

:

График плотности вероятности f(x)

График функции распределения F(x)

Задачи контрольных и самостоятельных работ

Задача 1

НСВ на всей
числовой оси oX задана интегральной функцией:

Найти
вероятность, что в результате 2 испытаний случайная величина примет значение,
заключенное в интервале (0;4).

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 2

Дана
дифференциальная функция непрерывной СВ Х. Найти: постоянную С, интегральную
функцию F(x).

Задача 3

Случайная
величина Х задана функцией распределения F(x):

а) Найти
плотность вероятности СВ Х — f(x).

б) Построить графики
f(x), F(x).

в) Найти вероятность
попадания НСВ в интервал (0; 3).

Задача 4

Дифференциальная
функция НСВ Х задана на всей числовой оси ОХ:

Найти:

а) постоянный
параметр С=const;

б) функцию
распределения F(x);

в) вероятность
попадания в интервал -4<X<4;

г) построить
графики f(x), F(X).

Задача 5

Случайная величина
Х задана функцией распределения F(x):

а) Найти
плотность вероятности СВ Х — f(x).

б) Построить
графики f(x), F(x).

в) Найти
вероятность попадания НСВ в интервал (0;π⁄2).

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 6

НСВ X имеет
плотность вероятности (закон Коши)

а) постоянный
параметр С=const;

б) функцию
распределения F(x);

в) вероятность
попадания в интервал -1<X<1;

г) построить
графики f(x), F(X).

Задача 7

Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:

а) найти
параметр C;

б) при
заданной интегральной функции F(x) найти дифференциальную
функцию f(x), а при заданной дифференциальной функции f(x) найти интегральную
функцию F(x);

в)
построить графики функций F(x) и f(x);

г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(X);

д)
вычислить вероятность попадания в интервал P(a≤x≤b);

е)
определить, квантилем какого порядка является точка xp;

ж)
вычислить квантиль порядка p

Задание 8

Дана
интегральная функция распределения случайной величины X. Найти дифференциальную
функцию распределения, математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение.

Задача 9

Случайная
величина X задана интегральной функцией распределения

Найти
дифференциальную функцию, математическое ожидание и дисперсию X.

Задача 10

СВ Х
задана функцией распределения F(x). Найдите вероятность
того, что в результате испытаний НСВ Х попадет в заданный интервал (0;0,5).
Постройте график функции распределения. Найдите плотность вероятности НСВ Х и
постройте ее график. Найдите числовые
характеристики НСВ Х, если

  • Краткая теория
  • Примеры решения задач
  • Задачи контрольных и самостоятельных работ
Источник


2.4.4. Как вычислить математическое ожидание и дисперсию НСВ?

Ответ на этот вопрос состоит из двух слов: с помощью интегралов.

Сам смысл математического ожидания и дисперсии мы уже разбирали ранее (но, конечно, повторим), и сейчас настало время узнать, как они определяются для непрерывной случайной величины. Всё очень просто, по аналогии с ДСВ:

Математическое ожидание непрерывной случайной величины  определяется, как несобственный интеграл:
, где  – функция плотности распределения этой случайной величины.
Дисперсия тоже имеет «знакомые очертания»:  (по определению), но в практических задачах гораздо удобнее применять формулу:
 

Как и в дискретном случае, дисперсия не может быть отрицательной!

И среднее квадратическое отклонение вычисляется точно так же:

Итак, все инструменты в руках и мы с энтузиазмом приступаем к любимому делу:

Задача 110
Непрерывная случайная величина  задана функцией

Вычислить . И построим ещё графики  и , ну а куда же без них? Повторение и ещё раз повторение!

Решение начнём как раз с графика функции распределения. При его ручном построении  удобно найти промежуточное значение  и аккуратно провести кусок кубической параболы :

Повторяем: функция распределения  описывает вероятность того, что случайная величина  примет значение, МЕНЬШЕЕ, чем переменная , «пробегающая» все значения от  до .  Данная функция изменяется в пределах  и не убывает (т. к. «накапливает» вероятности). Но если в дискретном случае она разрывна (вспоминаем «ступеньки»), то здесь – всюду непрерывна!

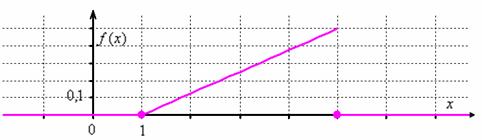
Очевидно, что случайная величина  принимает случайные значения из отрезка , и какие из них более вероятны, а какие – менее, наглядно показывает функция ПЛОТНОСТИ распределения вероятностей:

Найдём опорные точки параболы: , и готово:

В отличие от , функции плотности может быть разрывна и может принимать значения бОльшие единицы (как в нашем случае); может, как убывать, так и возрастать и даже иметь экстремумы (наш кусок параболы растёт). Однако (повторяем), она неотрицательна:   и обладает свойством , и это лучше всегда проверять (а то мало ли, опечатка или ошибка). Неотрицательность функции очевидна по чертежу, а вот интеграл подлежит вычислению. Используя свойство аддитивности, делим его на три части:

 – данный результат равен заштрихованной площади (см. выше) и с вероятностной точки зрения означает тот факт, что случайная величина  достоверно примет одно из значений отрезка . Причём, по чертежу хорошо видно, что значения из правой части отрезка гораздо более вероятны, чем значения слева.

И эти вероятности оцениваются кусками площади, а не значениями функции !!! (окончательно избавляемся от распространённой иллюзии)

Ради интереса вычислим:
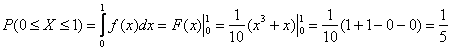
 – вероятность того, что случайная величина  примет какое-нибудь значение из промежутка

Теперь числовые характеристики. Очевидно, что математическое ожидание (среднеожидаемое значение) случайной величины  должно находиться в «живом» отрезке , причём – ближе к его правому концу (поскольку там выше плотность вероятности).

Убедимся в этом аналитически. По формуле вычисления математического ожидания, и в силу того же свойства аддитивности:


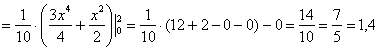
 – ну что же, вполне и вполне правдоподобно, результат я отметил красной точкой на чертеже.

! Примечание: в общем случае (и в этом, в частности)  не делит площадь на 2 равные части!

Если промежуток конечен, то можно сразу записывать, что матожидание равно определённому интегралу:
 

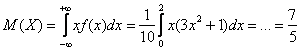
Дисперсию (меру рассеяния случайных значений относительно ) вычислим по формуле:

Сначала удобно разделаться с интегралом, здесь я не буду расписывать подробно:

Таким образом:

И, наконец, среднее квадратическое отклонение:

Вот такое вот у нас получилось захватывающее повторение-изучение-исследование! И коль скоро спрашивалось немного, запишем:

ответ:

Строго говоря, ответ следовало записывать и в предыдущих задачах, но когда пунктов много, то итоговые результаты вполне допустимо помечать по ходу решения, например, подчёркивать или обводить карандашом.

Следующее задание для самостоятельного решения:

Задача 111
Дана функция:

Представить  в аналитическом виде и показать, что она может служить плотностью вероятностей случайной величины . Вычислить  и 

Справка: уравнение прямой, проходящей через точки , можно составить по формуле .
Бывает, вычисление матожидания и дисперсии сопряжено с техническими трудностями, и в соответствующей статье сайта я рассмотрел следующие функции:

Однако вся трудность этих заданий состоит в более сложных интегралах, что, собственно, уже не относится к теории вероятностей, и посему я не включил эти примеры в настоящую книгу. Но вот задачка с несобственными интегралами не помешает:

Задача 112
Непрерывная случайная величина  задана плотностью распределения вероятностей:

Найти  и . Составить функцию распределения и построить графики . Вычислить вероятность того, что случайная величина  примет значение, бОльшее, чем её математическое ожидание.

Попробуйте решить её самостоятельно! И для желающих есть более трудное задание с функцией  (смотрите опять же на сайте – ссылка выше).

Но этим всё дело не ограничивается. Точно так же, как и в дискретном случае, у непрерывной случайной величины существуют особые законы распределения вероятностей, и наиболее популярные из них мы рассмотрим прямо сейчас:

2.5.1. Равномерное распределение вероятностей

2.4.3. Функция ПЛОТНОСТИ распределения вероятностей

| Оглавление |



Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Понравилась статья? Поделить с друзьями:
  • Взвешенные вещества в воде как найти
  • Как найти рисунок в интернете по фото
  • Как найти объем продаж в ценах
  • Как найти обои по фото для стен
  • Как составить меню по хлебным единицам