Как найти матрицу длин путей

Справка по идз «Графы»

Скелет
графа общего вида.
В
случае, когда при исследовании графа
L=(X.U;P) общего вида требуется не полная
информация о нём, а лишь знание того,
какие пары его различных вершин смежны
и какие нет, прибегают к носителю такой
информации – скелету
графа
L, который обозначим как

.
Граф

относится к классу обыкновенных графов
с множеством вершин тем же, что и в графе
L, и новым множеством рёбер

,
определённым следующим образом:

1. если
   в графе L есть петли, то они удаляются;

2. если
   в графе L есть дуги, то производится
   дезориентация дуг;

3. если
   в графе L есть кратные рёбра, то они
   заменяются одним эквивалентным
   ребром-звеном;

4. оставшиеся
   рёбра образуют множество рёбер

   .

Таким
образом, множество рёбер

состоит из рёбер, полученных из множества
U после выполнения описанных выше
процедур 1, 2, 3.

1.3. Определение числа маршрутов длины «l» на графе

Маршрутом
_i,j
в графе G=(X,U) называется конечная
последовательность вершин и рёбер вида
–

_0,l
=( x₀,u₁,x₁,u₂,x₂,…,x_l–1,u_k,
x_l
),

где
x₀,
x_l
– соответственно начальная и конечная
вершины маршрута _0,l
.

Очевидно,
в конечном графе G=(X,U) можно выделить
только конечное число маршрутов. Длина
маршрута _i,j
равна числу рёбер, которые в него входят.

Часто
требуется знать, сколько маршрутов
заданной длины в графе G связывает
вершину x_i
с вершиной x_j
.

Для
определения маршрутов длины q в графе
G=(X,U) его матрицу смежности R возводят
в степень, равную q. Тогда для каждого
значения степени q=1,2,…,k значение
элемента (r_i,j)^q
матрицы R^q
определяет количество маршрутов _i,j
длиной,
равной значению степени q.

Рисунок
3

ПРИМЕР.
Для графа G= (X,U) , представленного на
рисунке 3, определить количество
маршрутов длины, равной 2.

Матрица
смежности R графа G имеет вид:

R=

	X1	X2	X3	X4
X1	0	1	1	0
X2	1	0	0	1
X3	1	0	0	1
X4	0	1	1	0

Возведем
матрицу R в квадрат:

R²=

	X1	X2	X3	X4
X1	2	0	0	2
X2	0	2	2	0
X3	0	2	2	0
X4	2	0	0	2

Значение
каждого элемента r_i,j
матрицы R²
равно числу маршрутов длины 2, ведущих
из вершины x_i
в вершину x_j.

Например,
r_3,2=2
означает, что в графе два маршрута
длины 2, которые ведут из вершины x₃
в вершину x₂
. Запишем их:

_3,2=x_3,3,x₁,1,x₂;
_3,2
=x₃,4,x₄,2,x₂.

Задание
4.

Для
графа, представленного на рисунке 1
выполнить следующее:

4.1.
Привести примеры подграфов 3-х вершинных,
4-х вершинных, 1-вершинных.

4.2.
Привести пример суграфа данного графа.

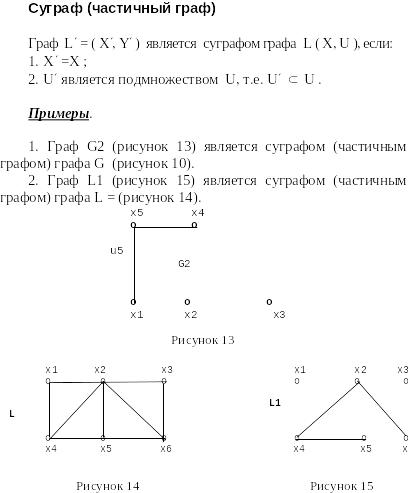
4.3.
Выполнить унарные операции для вершин,
помеченных *.

Задание
5.

Для
графа G=(X,U)
(
рисунок 1)
выполнить следующее:

5.1.
Построить матрицу метрики (отклонений).

5.2.
Вычислить радиус и диаметр.

5.3.
Определить периферийные точки.

Способ
нахождения метрики графа

Для
нахождения метрики

=

графа L = (X,U) достаточно знать его матрицу
смежности R={ r_i,j}
над булевой алгеброй B = ( 0,1 ), т.е.
элементы матрицы r_i,j
= 1, если вершины x_i
и x_j
– смежны и r_i,j
= 0, в противном случае, все действия
над элементами матрицы R производятся
по правилам логической
алгебры:

1
+ 1 = 1; 0 + 0 = 0; 1 + 0 = 1; 0 * 0 = 0; 1 * 0 = 0.

Сопоставляя
уже известные нам способы для установления
существования маршрутов в графе длины
q = m, можно утверждать, что при возведении
в степень
матрицы S = R + E, где Е – единичная
матрица той же размерности, что и
размерность матрицы R, на
некотором шаге возведения в степень
получим:

S
= S^k+1,
т.е. устойчивую
матрицу S в
степени «k».

Значения
степеней p матрицы S^p:
p= {k, k–1, k–2, … , 1} равны
длинам простых кратчайших цепей,
связывающих вершины x_i
и x_j.

Таким
образом, последовательно возводя в
степень p = {1, 2, 3,…, k} матрицу S до
получения устойчивой матрицы S^k,
можно определить расстояния между всеми
вершинами графа L=(X,U), построив матрицу
метрики графа L.

Алгоритм
построения матрицы метрики графа

Исходные
данные для построения матрицы метрики
(отклонений):

1.
Граф L=(X,U).

2.
Матрица смежности R графа L c элементами
логического типа:

 1,
если вершины x_i,
x_j
– смежны;

r_i,j

= 

0
в противном случае.

Введем
обозначения:

R
– матрица смежности заданного графа
L;

E
– единичная матрица;

М
– матрица метрики (отклонений).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень) 

§17. Графы.

---

Что такое граф?

Ключевые слова:

• граф	
• вершина	
• ребро	
• матрица смежности	
• степень вершины	
• связный граф
• взвешенный граф
• весовая матрица
• ориентированный граф
• оптимальный путь
• количество путей

Давайте подумаем, как можно наглядно представить такую информацию:

От пос. Васюки три дороги идут в Солнцево, Грибное и Ягодное. Между Солнцевом и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное.
Нарисуйте в тетради схему дорог по этому описанию.

Можно, например, нарисовать такую схему (рис. 3.17, а).

Рис. 3.17

В информатике для исследования таких схем используют графы.

Граф — это набор вершин (узлов) и связей между ними — рёбер.

Граф, соответствующий нашей схеме дорог, показан на рис. 3.17, б, для краткости населённые пункты обозначены латинскими буквами.

Матрица смежности графа

Для хранения информации об узлах и связях показанного выше графа можно использовать таблицу такого вида (рис. 3.18).

Рис. 3.18

Единица на пересечении строки А и столбца В означает, что между вершинами А и В есть связь. Ноль указывает на то, что связи нет. Такая таблица называется матрицей смежности. Она симметрична относительно главной диагонали (см. закрашенные клетки в таблице).

Исследуйте матрицу смежности и сравните её с графом на рис. 3.17, б. Что означает единица на пересечении столбца С и строки С?

В этом графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.

Степенью вершины называют количество рёбер, с которыми связана вершина. При этом петля считается дважды (с вершиной связаны оба конца ребра!).

Подсчитайте по матрице смежности, сколько ребёр в графе. Определите степени всех вершин. Как вы рассуждали?

Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (например, как на рис. 3.17, б), но матрица смежности не даёт никакой информации о том, как именно располагать вершины друг относительно друга. Для таблицы, приведённой выше, возможны, например, такие варианты (рис. 3.19).

Рис. 3.19

Нарисуйте по матрице смежности (рис. 3.20) два разных изображения графа.

Рис. 3.20

Граф имеет 4 вершины, причём каждая вершина связана рёбрами со всеми остальными. Нарисуйте этот граф. Сколько всего рёбер в этом графе?

Граф имеет N вершин, причём каждая вершина связана рёбрами со всеми остальными. Сколько всего рёбер в этом графе?

Граф имеет 4 ребра. Чему равна сумма степеней вершин в этом графе? Зависит ли она от количества вершин?

Граф имеет N рёбер. Чему равна сумма степеней вершин в этом графе?

Попробуйте нарисовать граф с пятью вершинами, где все вершины имеют степень 3. Получилось ли у вас? Почему?

Связный граф

В графе на рис. 3.17, б все вершины связаны: между любой парой вершин существует путь — последовательность вершин, в которой каждая следующая связана ребром с предыдущей. Такой граф называется связным.

Связный граф — это граф, между любыми вершинами которого существует путь.

Теперь представьте себе, что дороги Васюки-Солнцево, Васю- ки-Грибное и Грибное-Ягодное завалило снегом (или размыло дождём) так, что по ним ни пройти, ни проехать (рис. 3.21).

Рис. 3.21

Эту схему тоже можно считать графом (она соответствует определению), но в таком графе есть две несвязанные части, каждая из которых — связный граф. Такие части называют компонентами связности.

Постройте матрицу смежности графа, изображённого на рис. 3.21.

Граф имеет 4 вершины и две компоненты связности. Какое наибольшее количество рёбер может быть в этом графе, если в нём нет петель? Нарисуйте этот граф.

Вспоминая материал предыдущего параграфа, можно сделать вывод, что дерево — это частный случай связного графа. Но у него есть одно важное свойство — в дереве нет замкнутых путей — циклов, т. е. путей, которые начинаются и заканчиваются в одной и той же вершине.

Найдите все циклы в графе на рис. 3.17.

Дерево — это связный граф, в котором нет циклов.

Взвешенный граф

Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).

Рис. 3.22

Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.

Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.

Как хранить информацию о таком графе? Ответ напрашивается сам собой — нужно в таблицу записывать не 1 или 0, а вес ребра. Если связи между двумя узлами нет, на бумаге можно оставить ячейку таблицы пустой, а при хранении в памяти компьютера записывать в неё условный код, например, число -1 или очень большое число. Такая таблица называется весовой матрицей, потому что содержит веса рёбер. В данном случае она выглядит так (рис. 3.23).

Рис. 3.23

Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.

Что означают пустые ячейки в весовой матрице?

Как по весовой матрице сразу определить, сколько рёбер в графе?

Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?

Рис. 3.24

Оптимальный путь в графе

Для того чтобы определить оптимальный (наилучший) путь между двумя вершинами графа, нужно ввести какой-то числовой показатель, по которому можно сравнивать пути — определять, какой из них лучше. Обычно для оценки пути используют сумму весов ребёр, входящих в этот путь. Например, при поиске кратчайшего пути чем меньше это значение, тем лучше.

Какие показатели вы используете в жизни для определения оптимального пути? Всегда ли самый короткий путь — самый лучший?

Если в графе немного узлов, по весовой матрице можно легко определить оптимальный путь из одной вершины в другую простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей на рис. 3.25 (числа определяют стоимость поездки между соседними пунктами).

Рис. 3.25

Найдём наилучший путь из А в В — такой, при котором общая стоимость поездки минимальная.

Для решения задачи будем строить дерево перебора вариантов. Видим, что из пункта А напрямую

Рис. 3.26

Числа около рёбер обозначают стоимость поездки по этому участку, а индексы у названий узлов показывают общую стоимость проезда в данный узел из узла А. Теперь разберём варианты дальнейшего движения из узла С I tM lt;pb р (рис. 3.27).

Рис. 3.27

Почему, на ваш взгляд, на схеме не показана возможность движения из С в А?

Видим, что из С сразу можно попасть в В, стоимость проезда в этом случае равна 7.

Почему нельзя на этом остановиться, ведь путь из А в В найден?

Проверяя пути через узел В, выясняем, что можно сократить стоимость до 6 (рис. 3.28)

Рис. 3.28

Нужно ли исследовать дальше путь, содержащий цепочку ACED? Сравните стоимость этого пути и стоимость уже найденного пути из А в В.

Аналогично строим вторую часть схемы (рис. 3.29).

Рис. 3.29

Таким образом, оптимальный (наилучший) путь — ADEB, его стоимость — 3.

Нужно ли проверять пути ACED и ADEC, не дошедшие до узла В? Могут ли они улучшить результат?

Конечно, для более сложных графов метод перебора работает очень долго, поэтому используются более совершенные (но значительно более сложные) методы.

Ориентированный граф

Наверное, вы заметили, что при изображении деревьев, которые описывают иерархию (подчинение), мы ставили стрелки от верхних уровней к нижним. Это означает, что для каждого ребра указывается направление, и двигаться можно только по стрелкам, но не наоборот.

Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление.

Орграф может служить, например, моделью системы дорог с односторонним движением. Матрица смежности и весовая матрица для орграфа уже не обязательно будут симметричными.

На схеме на рис. 3.30 всего две дороги с двусторонним движением, по остальным можно ехать только в одну сторону.

Рис. 3.30

Рёбра в орграфе называют дугами. Дуга, в отличие от ребра, имеет начало и конец.

Нарисуйте граф по весовой матрице, показанной на рис. 3.31. С помощью дерева перебора найдите все возможные пути из вершины А в вершину Е, не проходящие дважды через одну и ту же вершину, и стоимости проезда по каждому из этих путей. Определите оптимальный путь из вершины А в вершину Е.

Рис. 3.31

---

Количество путей

Определим количество возможных путей из вершины А в вершину К для ориентированного графа, показанного на рис. 3.32.

Рис. 3.32

Так как граф ориентированный, переходить в другую вершину можно только по стрелкам.

В графе на рис. 3.32 есть одна начальная вершина А, из которой дуги только выходят. Такая вершина называется истоком. Вершина, в которую дуги только входят (и ни одна не выходит), называется конечной вершиной или стоком. В нашем графе сток — это вершина К.

По весовой матрице на рис. 3.31 найдите исток и сток в графе. Как вы рассуждали?

Будем двигаться по стрелкам от начальной вершины А. Около каждой вершины запишем количество возможных путей из вершины А в эту вершину. В вершину А существует единственный путь — пустой (никуда не ехать). Найдём все вершины, в которые можно приехать только из А: это вершины Б и Г, записываем около них количество путей 1 (рис. 3.33).

Рис. 3.33

Теперь ищем вершины, в которые можно попасть только из уже отмеченных вершин. Например, в вершину В есть один путь из А напрямую, а также по одному пути через Б и Г (так как эти вершины отмечены числом 1). Общее количество путей из А в Б равно сумме отметок предыдущих вершин: для вершины В получаем 3 пути. В вершину Ж можно попасть только из Г, поэтому число путей в Г и Ж совпадает (рис. 3.34).

Рис. 3.34

В вершину Д идёт один путь через Б и три пути через В, поэтому общее число путей — 4. Аналогично получаем 4 пути в вершину Е: 3 пути через В и один через Ж (рис. 3.35).

Рис. 3.35

Далее находим один путь из А в И (только через Ж) и 4 пути из А в 3 (все через Д). В конечную вершину К можно приехать через вершины Д (4 пути), 3 (4 пути), Е (4 пути) и И (1 путь), таким образом, общее количество различных путей равно 13 (рис. 3.36).

Рис. 3.36

---

Выводы

• Граф — это набор вершин (узлов) и связей между ними — рёбер.
• Матрица смежности — это таблица, в которой единица на пересечении строки и столбца обозначает ребро между соответствующими вершинами, а ноль — отсутствие ребра.
• Связный граф — это граф, между любыми вершинами которого существует путь.
• Цикл — это замкнутый путь в графе.
• Дерево — это связный граф, в котором нет циклов.
• Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра. Взвешенный граф описывается весовой матрицей.
• Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление. Рёбра орграфа называют дугами. Матрица смежности и весовая матрица орграфа могут быть несимметричными.

Нарисуйте в тетради интеллект-карту этого параграфа.

---

Вопросы и задания

1. Можно ли сказать, что лес (множество деревьев) — это граф? Почему?
2. Как по матрице смежности определить, есть ли петли в графе?
3. Как по весовой матрице определить длину пути в графе?
4. Когда для представления данных используются орграфы? Приведите примеры.
5. Выполните по указанию учителя задания в рабочей тетради.

---

Оглавление

§16. Списки и деревья.

§17. Графы.

§18. Игровые стратегии.

---

Учитывая прямоугольный путь в виде двоичной матрицы, найдите длину максимально длинного маршрута от источника до пункта назначения, перемещаясь только к ненулевым соседним позициям, т. Е. Мы можем сформировать маршрут из позиций, имеющих значение 1. Примечание. в выходном пути не должно быть циклов.

Например, самый длинный путь от исходной ячейки (0, 0) в ячейку назначения (5, 7) имеет длину 22 для следующей матрицы.

(0, 0) —> (1, 0) —> (2, 0) —> (2, 1) —> (2, 2) —> (1, 2) —> (0, 2) —> (0, 3) —> (0, 4) —> (1, 4) —> (1, 5) —> (2, 5) —> (2, 4) —> (3, 4) —> (4, 4) —> (5, 4) —> (5, 5) —> (5, 6) —> (4, 6) —> (4, 7) —> (4, —> (5, —> (5, 7)

Потренируйтесь в этой проблеме

 
Мы можем использовать Backtracking Для решения этой проблемы. Мы начинаем с данной исходной ячейки в матрице и исследуем все четыре возможных пути и рекурсивно проверяем, приведут ли они к месту назначения или нет. Мы должны отслеживать расстояние текущей ячейки от источника и обновлять значение самого длинного пути, найденного до сих пор, при достижении ячейки назначения. Если путь не достигает пункта назначения или не изучены все возможные маршруты из текущей ячейки, выполните возврат. Чтобы убедиться, что путь прост и не содержит циклов, отслеживайте ячейки, участвующие в текущем пути, в матрице, и перед исследованием любой ячейки игнорируйте ячейку, если она уже покрыта текущим путем.

Ниже приведена реализация этой идеи на C++, Java и Python:

Временная сложность приведенного выше решения экспоненциальна и требует дополнительного места для рекурсии (стека вызовов).