Аннотация: Рассматриваются вопросы достижимости для орграфов и способы нахождения матриц достижимости и контрдостижимости. Рассматривается матричный способ нахождения количества путей между любыми вершинами графа, а также нахождение множества вершин, входящих в путь между парой вершин. Цель лекции: Дать представление о достижимости и контрдостижимости и способах их нахождения
Достижимость и контрдостижимость
Задач, в которых используется понятие достижимости, довольно много. Вот одна из них. Граф может быть моделью какой-то организации, в которой люди представлены вершинами, а дуги интерпретируют каналы связи. При рассмотрении такой модели можно поставить вопрос, может ли информация от одного лица хi быть передана другому лицу хj, т. е. существует ли путь, идущий от вершины хi к вершине хj. Если такой путь существует, то говорят, что вершина хj достижима из вершины хi. Можно интересоваться достижимостью вершины хj из вершины хi только на таких путях, длины которых не превосходят заданной величины или длина которых меньше наибольшего числа вершин в графе и т. п. задачи.
Достижимость в графе описывается матрицей достижимости R=[rij], i, j=1, 2, … n, где n – число вершин графа, а каждый элемент определяется следующим образом:
rij=1, если вершина хj достижима из хi,
rij=0, в противном случае.
Множество вершин R(xi) графа G, достижимых из заданной вершины xi, состоит из таких элементов xj, для которых (i, j)-й элемент в матрице достижимостей равен 1. Очевидно, что все диагональные элементы в матрице R равны 1, поскольку каждая вершина достижима из себя самой путeм длины 0. Поскольку прямое отображение 1-го порядка Г+1(xi) является множеством таких вершин xj, которые достижимы из xi с использованием путей длины 1, то множество Г+(Г+1(xi)) = Г+2(xi) состоит из вершин, достижимых из xi с использованием путей длины 2. Аналогично Г+p(xi) является множеством вершин, которые достижимы из xi с помощью путей длины p.
Так как любая вершина графа, которая достижима из xi, должна быть достижима с использованием пути (или путей) длины 0 или 1, или 2, …, или p, то множество вершин, достижимых для вершины xi, можно представить в виде
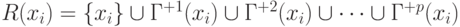
Как видим, множество достижимых вершин R(xi) представляет собой прямое транзитивное замыкание вершины xi, т. е. R (xi) = T+(xi). Следовательно, для построения матрицы достижимости находим достижимые множества R (xi) для всех вершин 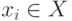
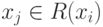
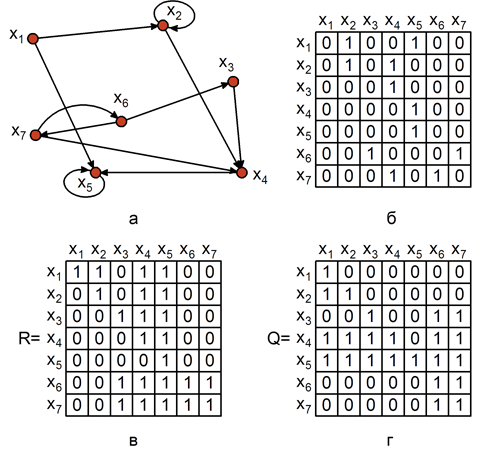
Рис.
4.1.
Достижимость в графе: а –граф; б – матрица смежности; в – матрица достижимости; г- матрица контрдостижимости.
Для графа, приведенного на
рис.
4.1,а, множества достижимостей находятся следующим образом:

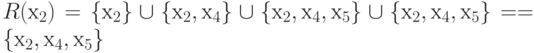

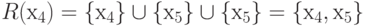
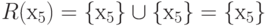
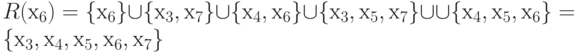
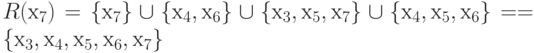
Матрица достижимости имеет вид, как показано на
рис.
4.1,в. Матрицу достижимости можно построить по матрице смежности (
рис.
4.1,б), формируя множества T+(xi) для каждой вершины xi
.
Матрица контрдостижимости Q = [ qij], i, j =1, 2, … n, где n – число вершин графа, определяется следующим образом:
qij=1, если из вершины xj
можно достичь вершину xi
,
qij=0, в противном случае.
Контрдостижимым множеством Q (xi) является множество таких вершин, что из любой вершины этого множества можно достичь вершину xi
. Аналогично построению достижимого мно-жества R (xi) можно записать выражение для Q (xi):
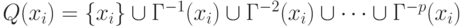
Таким образом, видно, что Q (xi) – это есть не что иное как обратное транзитивное замыкание вершины xi
, т. е. Q (xi) = Т—xi). Из определений очевидно, что столбец xi
матрицы Q (в котором qij=1, если 
матрицы R, т. е. Q = RT,где RT
– матрица, транспонированная к матрице достижимости R.
Матрица контрдостижимости показана на
рис.
4.1,г.
Следует отметить, что поскольку все элементы матриц R и Q равны 1 или 0, то каждую строку можно хранить в двоичной форме, экономя затраты памяти ЭВМ. Матрицы R и Q удобны для обработки на ЭВМ, так как с вычислительной точки зрения основными операциями являются быстродействующие логические операции.
Рассматриваются вопросы достижимости
для орграфов и способы нахождения матриц
достижимости и контрдостижимости.
Рассматривается матричный способ
нахождения количества путей между
любыми вершинами графа, а также нахождение
множества вершин, входящих в путь между
парой вершин. Цель лекции: Дать
представление о достижимости и
контрдостижимости и способах их
нахождения
Достижимость и
контрдостижимость
Задач, в которых используется понятие
достижимости, довольно много.
Вот одна из них. Графможет быть
моделью какой-то организации, в которой
люди представлены вершинами, а дуги
интерпретируют каналы связи. При
рассмотрении такой модели можно поставить
вопрос, может ли информация от одного
лицахiбыть передана другому лицухj, т. е. существует ли путь, идущий от
вершиныхiк вершинехj. Если такой путь существует, то говорят,
что вершинахjдостижимаиз вершиныхi.
Можно интересоваться достижимостью
вершиныхjиз вершиныхiтолько на таких путях, длины которых не
превосходят заданной величины или длина
которых меньше наибольшего числа вершин
в графе и т. п. задачи.
Достижимость в графе описывается
матрицей достижимости R=[rij],
i, j=1, 2, … n, гдеn–
число вершин графа, а каждый элемент
определяется следующим образом:
rij=1,
если вершинахjдостижима изхi,
rij=0,
в противном случае.
Множество вершин R(xi)графаG, достижимых из
заданной вершиныxi, состоит из таких элементовxi, для которых(i, j)-й
элемент в матрице достижимостей равен
1. Очевидно, что все диагональные элементы
в матрицеRравны 1,
поскольку каждая вершина достижима из
себя самой путeм длины 0. Поскольку прямое
отображение 1-го порядкаГ+1(xi)является множеством таких вершинxj, которые достижимы изxiс использованием путей длины 1, то
множествоГ+(Г+1(xi))
= Г+2(xi)состоит из вершин, достижимых изxiс использованием путей длины 2. АналогичноГ+p(xi)является множеством вершин, которые
достижимы из xi с помощью путей
длиныp.
Так как любая вершина графа, которая
достижима из xi, должна быть достижима с использованием
пути (или путей) длины 0 или 1, или 2, …,
илиp, то множество
вершин, достижимых для вершиныxi, можно представить в виде
R (xi)
= { xi }
Г+1(xi)
Г+2(xi)
…
Г+p(xi).
Как видим, множество достижимых вершин
R(xi)представляет собой прямое транзитивное
замыкание вершиныxi, т. е.R(xi)
= T+(xi).
Следовательно, для построения матрицы
достижимости находим достижимые
множестваR(xi)для всех вершинxiX.
Полагая,rij=1,
еслиxj
R(xi)иrij=0в противном случае.
Рис. 4.1. Достижимость в графе: а –граф;
б – матрица смежности; в – матрица
достижимости; г- матрица контрдостижимости.
Для графа, приведенного на рис. 4.1,а,
множества достижимостейнаходятся
следующим образом:
R (х1) = { х1}{ х2, х5}
{ х2, х4, х5 }
{ х2, х4, х5} = { х1,
х2, х4, х5},
R (х2) = { х2}{ х2, х4}
{ х2, х4, х5}
{
х2, х4, х5} = { х2,
х4, х5},
R (х3) = { х3}{ х4}
{ х5}
{ х5 } = { х3, х4, х5},
R (х4) = { х4}{ х5}
{ х5} = { х4, х5},
R (х5) = { х5}{ х5} = { х5},
R (х6) = { х6}{ х3, х7}
{ х4, х6}
{ х3, х5, х7}
{ х4, х5, х6} = { х3,
х4, х5, х6, х7},
R (х7) = { х7}{ х4, х6}
{ х3, х5, х7}
{ х4, х5, х6} = { х3,
х4, х5, х6, х7}.
Матрица достижимостиимеет вид,
как показано на рис. 4.1,в.Матрицу
достижимости можно построить поматрице смежности(рис. 4.1,б), формируя
множестваT+(xi)для каждой вершиныxi.
Матрица контрдостижимостиQ
= [ qij],i, j =1, 2, … n, гдеn– число вершин графа, определяется
следующим образом:
qij=1,
если из вершиныxjможно достичь вершинуxi,
qij=0,
в противном случае.
КонтрдостижимыммножествомQ
(xi)является множество таких вершин, что
из любой вершины этого множества можно
достичь вершинуxi. Аналогично построению достижимого
множестваR (xi)можно записать выражение дляQ
(xi):
Q (xi)
= { xi }
Г-1(xi)
Г—2(xi)
…
Г-p(xi).
Таким образом, видно, что Q
(xi)– это есть не что иное как обратное
транзитивное замыкание вершиныxi, т. е.Q (xi)
= Т—(xi).
Из определений очевидно, что столбец
xiматрицыQ(в
которомqij=1,
еслиxj
Q (xi),
иqij=0в противном случае) совпадает со строкойxi
матрицыR, т. е.Q
= RT,гдеRT– матрица, транспонированная кматрице
достижимостиR.
Матрица контрдостижимостипоказана
на рис. 4.1,г.
Следует отметить, что поскольку все
элементы матриц RиQравны 1 или 0, то каждую строку можно
хранить в двоичной форме, экономя затраты
памяти ЭВМ. МатрицыRиQудобны для обработки
на ЭВМ, так как с вычислительной точки
зрения основными операциями являются
быстродействующие логические операции.
Нахождение
множества вершин, входящих в путь
Если необходимо узнать о вершинах графа,
входящих в эти пути, то следует вспомнить
определения прямого и обратного
транзитивных замыканий. Так как T+(xi)– это множество вершин, в которые есть
пути из вершиныxi,
аT–(хj)– множество вершин, из которых есть
пути вxj, тоT+(xi)
T–(xj)– множество вершин, каждая из которых
принадлежит, по крайней мере, одному
пути, идущему отxiкxj
. Эти вершины называются существенными
или неотъемлемыми относительно двух
концевых вершинxiиxj. Все остальные вершины графа называются
несущественными или избыточными,
поскольку их удаление не влияет на пути
отxiкxj.
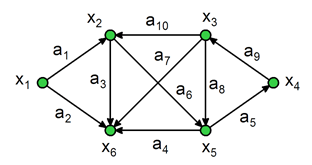
Рис. 4.2. Орграф
Так для графа на рис. 4.2 нахождение
вершин, входящих в путь, например из
вершины х2в вершинух4, сводится к нахождениюТ+(
х2)
={ х2,
х3,
х4,
х5,
х6},
Т—(
х4)
={ х1,
х2,
х3,
х4,
х5},
и их пересеченияT+(х2)
T–(х4)
={ х2,
х3,
х4,
х5}.
Матричный метод нахождения путей в
графах
Матрица смежности полностью определяет
структуру графа. Возведем матрицу
смежности в квадрат по правилам
математики. Каждый элемент матрицы А2
определяется по формуле
a(2)ik=nj=1aijajk
Слагаемое в формуле равно 1 тогда и
только тогда, когда оба числа aijиajk
равны 1, в противном случае оно равно
0. Поскольку из равенстваaij
= ajk
= 1следует существование пути длины
2 из вершиныxiв вершинухk, проходящего через вершинуxj, то (i -й,k-й) элемент матрицыА2равен числу путей длины 2, идущих изxiвхk.
В таблице 4.1a представлена матрица
смежности графа, изображенного на рис.
4.2. Результат возведения матрицы смежности
в квадрат А2показан в таблице 4.1б.
Так «1», стоящая на пересечении
второй строки и четвертого столбца,
говорит о существовании одного пути
длиной 2 из вершины х2к вершинех4. Действительно, как видим вграфена рис. 4.2, существует такой путь:a6,
a5. «2» в
матрицеA2говорит о существовании двух путей
длиной 2 от вершиных3к вершинех6:a8,
a4иa10,
a3.
Аналогично для матрицы смежности,
возведенной в третью степень A3
(таблица 4.1в),a (3)
ikравно числу
путей длиной 3, идущих отxiкхk. Из четвертой строки матрицыA3видно, что пути длиной 3 существуют: один
изх4вх4(a9,
a8,
a5),
один изх4в
х5(a9,
a10,
a6)и два пути изх4вх6(a9,
a10,
a3
и a9,
a8,
a4).
МатрицаA4показывает существование путей длиной
4 (таблица 4.1г).
Таким образом, если a р
ikявляется
элементом матрицыAр,тоa р
ikравно числу
путей (не обязательно орцепей или простых
орцепей) длиныр, идущих
отxiкхk.
Соседние файлы в папке МОТС
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Среди задач анализа ориентированных графов весьма важ-
важны следующие задачи.
- Вычисление для заданного ориентированного графа его
матрицы достижимости. Эту задачу будем называть
задачей построения транзитивного замыкания
ванного графа. Такое название связано с тем, что матрицу
достижимости можно рассматривать как матрицу
транзитивного и рефлексивного замыкания бинарного отношения
непосредственной достижимости в ориентированном графе. - Вычисление наименьших расстояний между всеми парами
вершин в ориентированном графе. Эту задачу будем называть
задачей о кратчайших расстояниях.
Задачу о кратчайших расстояниях можно сформулировать
так. Пусть задан взвешенный ориентированный граф и пусть
из вершины v достижима вершина w. Фиксируем какой-либо
путь S, ведущий из v в w. Расстоянием от вершины v до
вершины w по пути S называют сумму меток дуг, входящих в
этот путь, а наименьшим — минимальное из расстояний между
вершинами v и w по всем возможным путям.
Отметим, что задача о кратчайших расстояниях не всегда
имеет решение. Например, если в ориентированном графе есть
петля, метка которой — отрицательное число, то по этой петле
можно проходить сколько угодно раз и тем самым уменьшать
сумму меток дуг пути, включающего эту петлю, до любого
наперед заданного значения. - Перечисление всех путей между двумя произвольными
вершинами. Эту задачу будем называть задачей о
перечислении путей. При ее решении требуется для любой заданной
пары вершин u и v ориентированного графа получить все пути,
для которых u является началом, а v — концом.
Все указанные задачи (перечисленные в порядке возраста-
возрастания сложности) можно решить в рамках единого подхода, суть
которого сводится к следующему.
Ранее мы ввели понятие взвешенного неориентированного
(ориентированного) графа и метки ребер (дуг) определили как
числа, поставленные в соответствие ребру (дуге). Обобщим
это понятие для ориентированного графа.
Определение 5.13. Взвешенным (или размеченным)
ориентированным графом называют пару W = (G, φ), где
G = (V, Е) — обычный ориентированный граф, а φ: Е → R —
весовая функция (или функция разметки) со значениями
в некотором идемпотентном полукольце R = (R, +, ⋅, 0, 1),
причем (∀e ∈ Е)(φ(е) ≠ 0).
Мы будем в этом случае также говорить, что
ориентированный граф размечен над идемпотентным полукольцом R. Часто
полукольцо R является замкнутым, хотя это требование
необязательно. Будем, однако, везде в этом пункте предполагать,
что R — полукольцо с итерацией.
Пусть вершины ориентированного графа каким-либо
образом пронумерованы. Тогда взвешенный ориентированный граф
может быть задан матрицей А, элемент которой aij равен
значению φ((i,j)) весовой функции на дуге (i, j), если из вершины
i ведет дуга в вершину j, или нулю полукольца в противном
случае. Эту матрицу будем называть матрицей меток дуг.
Оказывается, что вычисление итерации А* матрицы А дает
решение всех сформулированных выше задач, если для каждой
задачи выбирать соответствующее полукольцо. А именно в
случае полукольца В (см. пример 3.2) получаем решение задачи о
транзитивном замыкании, в случае полукольца R+ (см.
пример 3.1) — решение задачи о кратчайших расстояниях*.
Будем называть задачу вычисления матрицы А* для
ориентированного графа, размеченного над произвольным
полукольцом с итерацией, в частности над замкнутым полукольцом,
общей задачей о путях во взвешенных ориентированных
графах.
В такой общности подхода, когда множество, казалось бы,
не связанных друг с другом задач решается единым
алгоритмом, „настраиваемым» на разные задачи выбором
соответствующего идемпотентного полукольца (т.е. разных областей
значений весовой функции), состоит несомненное преимущество
абстрактно-алгебраического подхода к решению таких задач
на графах.
*О методе решения третьей из сформулированных выше задач см.
задачу 7.36.
Рассмотрим теперь решение общей задачи о путях для
произвольного замкнутого полукольца R.
Метка пути, ведущего из вершины vi в вершину vj, есть
произведение в полукольце R меток входящих в путь дуг в
порядке их следования (для пути ненулевой длины) и есть 1
(единица полукольца R) для пути нулевой длины.
Стоимость прохождения из вершины vi в вершину vj
(или между i-й и j-й вершинами) — это сумма в полукольце R
меток всех путей, ведущих из вершины vi в вершину vj.
Заметим, что сумма, определяющая стоимость
прохождения, вообще говоря, есть бесконечная сумма замкнутого
полукольца, т.е. точная верхняя грань соответствующей
последовательности меток. Это связано с тем, что множество всех
путей, ведущих из одной вершины графа в другую, в общем
случае бесконечно (но, как можно доказать, не более чем счетно).
Аналогично можно определить стоимость прохождения из
вершины в вершину по какому-либо множеству путей.
Отметим, что если стоимость прохождения между парой вершин по
какому-либо множеству путей равна 0, то это означает, что не
существует пути, принадлежащего данному множеству путей,
ведущего из первой вершины рассматриваемой пары во вторую
вершину.
Матрица меток дуг является элементом полукольца матриц
над полукольцом R. В этом полукольце определены операции
сложения и умножения матриц, а также возведение матрицы в
неотрицательную степень. Докажем следующее утверждение.
Лемма 5.1. Элемент (l)ij матрицы Аl, l ≥ 0, равен
стоимости прохождения из вершины vi в вершину vj по всем путям
длины l.
◀ Доказательство проведем индукцией по l. При l = 0
утверждение очевидно, так как А0 = Е, где Е — единичная матрица,
которая будет матрицей стоимости прохождения по всем путям
длины 0.
При l = 1 утверждение также очевидно. Далее,
Согласно предположению индукции, элемент а(l-1)ik равен
стоимости прохождения из вершины vi в вершину vk по всем путям
длины l-1. Множество всех путей длины l из вершины vi в
вершину vj, проходящих через фиксированную k-ю вершину так,
что вершина vk связана дугой с вершиной vj (vk → vj,)
образуется путем присоединения дуги (vk, vj) к каждому из путей,
ведущих из vi в vk и имеющих длину l — 1.
 |
Тогда видно, что написанное выше |
Так как стоимость прохождения между парой вершин (vi,vj)
равна сумме меток всех путей, ведущих из первой вершины во
вторую, а указанную сумму можно можно получить, суммируя
последовательно метки путей длины 0, длины 1, длины 2 и т.д.,
то матрица стоимостей взвешенного ориентированного графа с
учетом доказанной леммы 5.1 может быть представлена в виде
До сих пор мы рассматривали матрицы над замкнутым
полукольцом. Однако, если элементы матрицы А принадлежат
некоторому полукольцу с итерацией, из теоремы 3.9 следует,
что и все элементы матрицы стоимостей С = А* останутся в
этом же полукольце. Таким образом, полученные результаты
можно перенести на произвольное полукольцо с итерацией.
Теорема 5.4. Матрица стоимостей ориентированного
графа G, размеченного над полукольцом с итерацией R (в
частности, над замкнутым полукольцом), равна итерации матрицы А
меток дуг ориентированного графа G. #
Для вычисления С = А* достаточно решить (т.е. найти
наименьшее решение) в R при всех j = 1,n систему уравнений
ξ = A ξ + εj,
где εj ∈ Rn — j-й единичный вектор, т.е. вектор, все элементы которого, кроме j-ro, равны 0, a j-й равен единице полукольца
R. Наименьшее решение имеет вид ξ = A*εj (см. 3.3). Тогда
столбец ξ = A*εj есть j-й столбец матрицы А*. Такой метод
вычисления матрицы А* аналогичен известному из линейной
алгебры методу элементарных преобразований при вычислении
обратной матрицы.
Выясним теперь смысл матрицы стоимостей С = А* для
полуколец В и R+.
В первом из этих полуколец метка отдельного пути всегда
равна 1 (так как метка дуги в размеченном над полукольцом
графе не может, согласно определению, быть нулем
полукольца). Следовательно, стоимость сij = 1, если существует хотя бы
один путь из i-й вершины в j-ю, и сij = 0, если иначе.
Другими словами, для полукольца сij матрица стоимостей совпадает с
матрицей достижимости ориентированного графа.
В полукольце R+ метка пути — это арифметическая сумма
меток его дуг, так как умножение в R+ — это обычное
арифметическое сложение. Поскольку сложение в R+ — это взятие
наименьшего из слагаемых, то стоимость сij — это
наименьшая из меток пути среди всех путей, ведущих из i-й вершины
в j-ю, т.е. это и есть наименьшая длина пути между
указанными вершинами. Таким образом, в полукольце R+ матрица
стоимостей является матрицей кратчайших расстояний, т.е.
наименьших длин путей между всеми парами вершин
ориентированного графа.
Пример 5.9. Рассмотрим граф, изображенный на рис. 5.27,
и решим для него задачу вычисления матрицы достижимости.
На числовые метки дуг внимания пока не обращаем, считая,
что ориентированный граф размечен над
полукольцом В и метка каждой дуги равна
1, т.е. ориентированный граф задан матрицей
Запишем систему уравнений в полукольце В для определения первого столбца матрицы А*
Отметим, что часто нулевые слагаемые не записывают, как и
в системах уравнений в поле действительных чисел.
Воспользуемся методом последовательного исключения
неизвестных (см. 3.3). Поскольку в правой части первого
уравнения нет переменной х1, можно исключить эту переменную из
системы, подставив в остальные уравнения. С учетом
идемпотентности сложения получим
Из второго уравнения имеем х2 = 1*(x3 + 0). В полукольце В
итерация любого элемента равна единице полукольца. Поэтому
х2 = х3 + 0. Исключив х2 из системы, получим
Далее вычислим х3 = 1*0 = 1 ⋅ 0 = 0. Подставив х3 = 0 в
последнее уравнение, найдем х4 = 1*1 = 1.
Итак, первый столбец А* есть
Второй столбец определяется из системы
Исключая х1, получаем
Из второго уравнения имеем х2 = 1*(х3 + 1) = х3 + 1. Далее находим
Отсюда х3 = 1*1 = 1 и х4 = х4 +1. В итоге х4 = 1*1 = 1, х2 = 1 + 1 = 1, х1 = 1 + 1 + 1 + 0 = 1. Таким образом, второй столбец
А* есть
Аналогично вычисляем третий и четвертый столбцы и в
результате получаем матрицу А*:
Анализ этой матрицы показывает (см. 5.2), что данный
граф связен и имеет две бикомпоненты: {v1, v4} и {v2, v3}.
Заметим, что в полукольце В можно упростить решение
систем уравнений, воспользовавшись свойствами полукольца.
Легко видеть, что наименьшее решение уравнения
есть xk = 1 и не зависит от значений переменных в правой части
уравнения. С учетом этого решение системы (5.3) упростится.
Так, из первого уравнения сразу получаем х1 = 1. Тогда
четвертое уравнение принимает вид х4 = x3 +1, откуда х4 = 1.
Поскольку х1 и х4 не входят в оставшиеся два уравнения, их
решение нужно искать, используя метод исключения.
Пример 5.10. Для графа, изображенного на рис. 5.27,
вычислим матрицу кратчайших расстояний, перейдя к полукольцу
R+. Договоримся, что для упрощения записи ∞ здесь будем
понимать как +∞.
Наш взвешенный ориентированный граф задается теперь
следующей матрицей:
Система для вычисления первого столбца матрицы А* имеет
вид
Обратим внимание на нюансы, связанные с работой в
полукольце R+: элементы 1 и 0 не являются единицей и нулем
полукольца, т.е. х ≠ x + 0 и х ≠ 1 ⋅ x в общем случае. Напомним,
что сложение в полукольце R+ — взятие наименьшего из двух
чисел, а умножение — обычное арифметическое сложение.
Заметим, что наличие слагаемого 0 в любой сумме (в полукольце)
означает, что вся сумма равна 0; слагаемое +∞ можно не
записывать (как нуль полукольца).
Из первого уравнения системы сразу следует, что х1 = 0,
так как одно из слагаемых в правой части есть элемент 0.
Напомним, что итерация любого элемента в рассматриваемом
полукольце равна единице полукольца. Учитавая этот факт, из
второго уравнения получаем
x2 = 2*(3x3 + ∞) = 3x3.
Исключая x2 из остальных уравнений системы и учитывая,
что x1 = 0, получаем
Далее, из второго уравнения имеем
x3 = (1 ⋅ 3)x3 + ∞ = 43 + ∞,
откуда x3 = 4* ⋅ ∞ = ∞, и поэтому
x3 = 3 ⋅ 0 + 4 ⋅ ∞ + ∞ = 3 + ∞ = 3
Подставляя найденное значение x3 в выражение для x2
получаем x2 = ∞. Первый столбец искомой матрицы вычислен:
Этот столбец содержит кратчайшие расстояния от всех вершин
графа до вершины v1. Наличие в нем нулей полукольца во
второй и третьей строках говорит о том, что вершина v1 не
достижима из вершин v2 и v3.
Аналогично вычисляются остальные столбцы матрицы А*.
Результат будет следующим:
Для данного простого ориентированного графа легко
сопоставить полученный алгебраический результат с результатом
„визуального» анализа ориентированного графа. Рассмотрим,
например, пару вершин (v1, v3). В ориентированном графе есть
различные пути из вершины v1 в вершину v3. Легко видеть,
что заведомо „не выгодны» пути, содержащие контуры и
петли, поэтому их рассматривать не будем и вычислим метки по
простым путям. По пути v1 → v4 → v3 сумма меток равна 5,
по пути v1 → v3 — 10, а по пути v1 → v2 → v3 — 8. Кратчайшее
расстояние — 5, что совпадает с ответом, полученным
алгебраически: элемент а*13 также равен 5. #
Помимо изложенного есть еще один способ вычисления
замыкания матрицы с элементами в замкнутом полукольце. Он
основан на понятии пути ранга k из вершины vi в вершину vj.
Пусть в ориентированном графе выбрана и зафиксирована
нумерация вершин. Будем полагать, что все вершины
пронумерованы подряд натуральными числами, начиная с 1.
Путь vi0 → vi1 → … → vim длины m называют путем ранга k
при m > 1, если k — наибольшее среди чисел i1, …, im-1 и
путем ранга 0 при m = 1. Путь нулевой длины также считают
путем ранга 0. Таким образом, ранг пути — это
максимальный номер вершины, в которую разрешено заходить по пути из
vi в vj (исключая вершины vi и vj). Путь ранга 0 не содержит
промежуточных вершин. Максимальный ранг пути в
ориентированном графе при указанном выше способе нумерации равен
числу его вершин.
Пример 5.11. В ориентированном графе, изображенном
на рис. 5.27, путь v1 → v4 → v1 имеет ранг 4, путь v4 → v1 → v2 — ранг 1, путь v4 → v1 → v3 → v2 — ранг 3. Пути
v4 → v3 → v2, v4 → v1 → v3 → v2 и v4 → v2 → v2 → v3 → v2 также
имеют ранг 3. #
Обозначим через Сk матрицу стоимостей прохождения
между различными парами вершин по всем путям ранга, не
превосходящего k. Ее элемент c(k)ij содержит стоимость
прохождения из вершины vi в вершину vj по всем путям рангов 0, …, k-1, k.
Выведем формулу для вычисления элемента c(k)ij матрицы Сk. Для этого заметим следующее. По пути ранга, не
большего k, из вершины vi в вершину vj можно пройти следующими
способами:
|
|
При первом способе следования стоимость прохождения из
вершины vi в vj по всем путям ранга, не большего л — 1,
составит c(k-1)ij.
При втором способе следования стоимость прохождения из
vi в vk по всем путям ранга, не большего л — 1, будет равна
c(k-1)ik. Стоимость прохождения из vk в vk по всем замкнутым
путям ранга, не большего k — 1, составит (c(k-1)kk)*.
Поясним это в частном случае, когда вершина vk
содержится в каком-то одном контуре. Пусть Г — такой контур, а μГ —
метка этого контура. Тогда очевидно, что метка пути,
образованного нуль-кратным прохождением по контуру Г, равна
единице полукольца (как метка всякого пути длины 0),
метка же пути, образованного m-кратным прохождением по Г при
m ≥ 1, равна μmГ. Следовательно, стоимость прохождения по
всем путям, которые получаются при произвольном числе
прохождений по контуру Г, составит
Стоимость прохождения из вершины vk в вершину vj по
пути ранга, не большего k — 1, равна c(k-1)kj (см. рис. 5.28).
Таким образом, стоимость прохождения по пути ранга, не
большего k, при указанном способе следования составит
c(k-1)ik (c(k-1)kk)* c(k-1)kj.
Таким образом, словесное описание «путешествия» из vi в vj
по путям ранга, не большего k, приводит к следующей формуле
для вычисления элемента матрицы Сk:
c(k)ij = c(k-1)ij + c(k-1)ik (c(k-1)kk)* c(k-1)kj. (5.5)
Пусть aij — элементы матрицы меток дуг
ориентированного графа. Поскольку каждый путь ранга 0 между
дающими вершинами состоит из одной дуги, а каждая вершина
достижима сама из себя по пути нулевой длины с меткой 1 или
по петле с меткой аii, то элементы матрицы С0 имеют вид
Тогда матрицу стоимостей С = А* можно найти, вычисляя
последовательно матрицы С(k) k = 0,n, по формулам (5.5)
и (5.6).
Вычисления по формулам 5.5 и 5.6 образуют алгоритм
Флойда — Уоршелла — Клини определения стоимости
прохождения между любыми парами вершин.
Для полуколец В и R+ в силу того, что в них итерация
любого элемента х равна единице полукольца, получим упрощенный
вариант формулы (5.5):
c(k)ij = c(k-1)ij + c(k-1)ik c(k-1)kj. (5.7)
Вычисления по формуле (5.7) начинают с матрицы
определяемой соотношением (5.6). Все дальнейшие вычисления
удобно также проводить в матричном виде. Для нахождения
матрицы С(k) удобно определить сначала матрицу D(k)
элементы которой вычисляются по формуле
d(k)ij = c(k-1)ik c(k-1)kj.
Чтобы найти j-й столбец матрицы D(k) достаточно k-й столбец
матрицы С(k-1) умножить (в смысле соответствующего
полукольца) на j-й элемент k-й строки этой же матрицы.
Решим описанным способом задачу о кратчайших
расстояниях в графе, изображенном на рис. 5.27. Для него С0 = А,
где матрица А имеет вид (5.4). Используя формулу (5.7),
следовательно находим
Например, матрица С(2) по матрице С(1) вычисляется так.
Сначала выделим в С(1) вторую строку и второй столбец:
Затем, чтобы вычислить первый столбец матрицы С(2),
берем второй (выделенный) столбец матрицы С(1) и умножаем (в
полукольце 7?+) его элементы по очереди на первый элемент
второй (выделенной) строки той же матрицы С(1). Каждое
такое произведение складываем в полукольце с одноименным
элементом первого столбца матрицы С(1). Поскольку
умножение в полукольце R+ — это арифметическое сложение, а
сложение — взятие наименьшего из двух чисел, мы получим
следующие элементы первого столбца матрицы С(2):
c(2)11 = min{c(1)11, c(1)12 + c(1)21} = min{0, ∞} = 0,
c(2)21 = min{c(1)21, c(1)22 + c(1)21} = min{∞, ∞} = ∞,
c(2)31 = min{c(1)31, c(1)32 + c(1)21} = min{∞, ∞} = ∞,
c(2)41 = min{c(1)41, c(1)42 + c(1)21} = min{3, ∞} = 3.
Как видим, первый столбец матрицы С(2) не изменился по
сравнению с первым столбцом матрицы С(1) Это означает, что
нельзя уменьшить стоимость прохождения в первую вершину
из других вершин графа, идя через вторую вершину (см.
рис. 5.27).
Точно так же для вычисления второго столбца матрицы С(2)
умножаем второй столбец С(1) на второй элемент второй
строки той же матрицы, для вычисления третьего столбца — на
третий элемент второй строки и т.д. Не выписывая подробно
всех вычислений, отметим характерный момент — изменение
элемента c(2)13 = 8 по сравнению с c(1)13 = 10, связанное с тем, что
стоимость прохождения из v1 в v3 по пути ранга 2 оказалась
меньше, чем стоимость прохождения по пути ранга 1.
Минимальная же стоимость прохождения c(4)13 = 5 получена по пути ранга 4.
Тема: Уравнения в идемпотентных полукольцах. Гомоморфизм графов. Алгоритмы обхода вершин графа.. Читаем, комментируем, решаем ДЗ.
Идемпотентные полукольца
Идемпотентным называется полукольцо, ,
в котором операция сложения идемпотентна: .
Примером таких полуколец являются:
В указанных полукольцах для каждого элемента можно ввести операцию итерации:
— бесконечная сумма степеней
элементов. Под степенью элемента понимается умножение его на себя
раз, а нулевая
степень равна единице полукольца по определению: .
Для приведённых выше полуколец итерация для любых элементов находится очень просто:
:
: для любого
Идемпотентные полукольца интересны тем, что в них можно решать уравнения вида:
Интересно, что такие необычные для арифметики уравнения как или
имеют здесь единственные решения:
Нахождение матрицы достижимости
Важной задачей в теории графов является нахождение матрицы достижимости по матрице
смежности. Можно доказать, что матрица достижимости может быть получена как итерация
матрицы смежности:
Таким образом, для получения матрицы необходимо решить
систем уравнений следующего
вида для :
где — элементы матрицы смежности, а
— элементы единичной
матрицы. Решением каждой из систем будет -й столбец матрицы
.
|
|
Рассмотрим пример. На рисунке 1 показан ориентированный граф из шести
вершин, матрица смежности которого равна:
- 1-й столбец
- 2-й столбец
- 3-6 столбцы
Полученная матрица достижимости примет вид:
Нахождение кратчайших путей
Теория графов широко применяется при решении транспортных задач — нахождения кратчайших
маршрутов в графах дорог, сетей и т.п. Для этого используются размеченные графы:
, где
— весовая функция над
некоторым полукольцом . Т.е. каждому ребру (или дуге)
сопоставляется число, символизирующее длину пути, сложнсть задачи или любую другую
стоимость перемещения между вершинами.
Рассмотрим граф, размеченный над полукольцом (см. рисунок 2).
|
|
Для такого графа можно записать матрицу метог дуг (эта матрица аналогична
матрице смежностей), где
В нашем случае матрица меток дуг равна:
Матрица стоимостей находится аналогично, с помощью решения
систем уравнений. Важно
отметить, что в данном случае вся работа ведётся в полукольце , в котором
нулём полукольца является , а единицей — 0!
- 1-й столбец
- 2-й столбец
- 3-6 столбцы
Полученная матрица стоимостей будет иметь вид:
Гомоморфизм и автоморфизм графов
Примеры гомоморфизма и не гомоморфизма представлены на рисунке 3.
|
|
Аналогичным образом гомоморфизм определяется для ориентированных графов. Рассмотрим
соответвтующий пример: для заданного графа (см. рисунок 4) необходимо
найти все друхвершинные гомоморфные образы.
|
|
Изоморфизм графа на себя (перестановка вершин) называется автоморфизмом.
Для анализа возможных существующих автоморфизмов в неориентированных графах удобно
использовать дополнения к графам: граф с тем же набором вершин и набором дуг, не
принадлежащих исходному графу. На рисунке 5 показан исходный граф и
его дополнение.
|
|
Можно увидеть, что любая перестановка из множества дополнении к графу оставит граф
неизменным:
Такие циклические перестановки можно записать в сокращённом виде:
Алгоритмы обхода графов. Поиск в глубину, поиск в ширину
Часто возникает задача обхода вершин и рёбер графа, т.е. посещение всех вершин или
рёбер, причём только по одному разу. Такой обход может использоваться, например, в поиске
информациии на графе. Существуют два широко известных алгоритма обхода вершин графа: поиск
в глубину и поиск в ширину. В обоих из них поиск ведётся от какой-то вершины, избранной в
качестве начальной.
Поиск в глубину использует в своей работе рекурсию (или стэк в явном виде). Основная идея
алгоритма состоит в «погружении» в граф от начальной вершины на максимально возможную
глубину, а затем постепенный возврат из рекурсивных вызовов.
С помощью рекурсии алгоритм поиска в глубину можно представить следующим образом:
bool visited[N] = {false, ... }; // массив флагов посещённых вершин
edge edges[M]; // массив рёбер
// рекурсивная процедура поиска
void deep_search(vertex_t v) {
visited[v] = true; // отметить вершину как посещённую
... // сделать с вершиной то, ради чего обход затевался
for(size_t i = 0; i < M; i++) {
edge e = edges[i];
if(e.from == v && !visited[e.to]) {
deep_search(e.to);
}
}
}
Если стэк использовать явным образом, можно избавиться от рекурсивного вызова:
bool visited[N] = {false, ... }; // массив флагов посещённых вершин
edge edges[M]; // массив рёбер
stack<vertex_t> s; // стэк
// нерекурсивная процедура поиска
void deep_search(vertex_t v0) {
s.push(v0);
while(!s.empty()) {
vertex_t v = s.pop();
if(visited[v]) continue; // пропустить посещённую вершину
visited[v] = true; // отметить вершину как посещённую
... // сделать с вершиной что-то
for(size_t i = 0; i < M; i++) {
edge e = edges[i];
if(e.from == v && !visited[e.to]) {
s.push(e.to);
}
}
}
}
В обоих случаях поиск запускается вызовом процедуры с параметром начальной вершины.
Рассмотрим пример поиска в глубину на неориентированном графе, изображённый не рисунке
6. Остовный подграф, получившийся при обходе вершин обозначен
пунктиром. Очевидно, что этот подграф является деревом с корнем в начальной вершине, а его
вид будет зависеть от порядка обхода вершин во внутреннем цикле рекурсивной процедуры.
|
|
Порядок следования вершин и состояние стэка на каждом шаге:
Аналогично производится поиск в глубину на ориентированном графе (см. рисунок
7).
|
|
С помощью алгоритма поиска в глубину можно классифицировать дуги ориентированного графа
следующим образом:
- остовные дуги
- получаются непосредственно при поиске в глубину, образуют дерево (или
в общем случае лес), на рисунке обозначены пунктиром; - прямые дуги
- соединяют предка и потомка в остовном пути, на рисунке обозначены
буквой F; - обратные дуги
- соединяют потомка и предка в остовном пути, на рисунке обозначены
буквой B, интересно то, что каждая из таких дуг задаёт элементарный контур в графе; - перекрёстные дуги
- все остальные дуги, на рисунке обозначены буквой C.
Вторым широко распространённым алгоритмом является поиск в глубину. Это алгоритм
использует очередь для хранения списка обрабатываемых вершин. В результате работы
алгоритмя также получается остовное дерево, которое в общем случае отличается от дерева
поика в глубину. Можно предложить следующий алгоритм поиска в ширину:
bool visited[N] = {false, ... }; // массив флагов посещённых вершин
edge edges[M]; // массив рёбер
queue<vertex_t> q; // очередь
// процедура поиска
void wide_search(vertex_t v0) {
q.push(v0);
while(!q.empty()) {
vertex_t v = q.pop();
if(visited[v]) continue; // пропустить посещённую вершину
visited[v] = true; // отметить вершину как посещённую
... // сделать с вершиной что-то
for(size_t i = 0; i < M; i++) {
edge e = edges[i];
if(e.from == v && !visited[e.to])
q.push(e.to);
}
}
}
|
|
Рассмотрим пример поиска в ширину на неориентированном графе, изображённый не рисунке
8. Остовный подграф, получившийся при обходе вершин обозначен
пунктиром. Порядок следования вершин и состояние очереди на каждом шаге представлены в табице:
Матрица достижимости простого ориентированного графа 

Содержание
- 1 Способы построения матрицы достижимости
- 1.1 Перемножение матриц
- 1.1.1 Случай нескольких путей
- 1.1.2 Пример
- 1.2 Алгоритм Уоршелла
- 1.1 Перемножение матриц
- 2 Связанные понятия
- 2.1 Матрица сильной связности
- 2.1.1 Построение матрицы сильной связности
- 2.1.2 Пример
- 2.2 Матрица связности графа
- 2.3 Матрица контрдостижимости
- 2.1 Матрица сильной связности
- 3 Примечания
Способы построения матрицы достижимости
Перемножение матриц
Пусть дан простой граф 




По определению, матрица композиции отношений 



После нахождения матриц 






Случай нескольких путей
Если булевы операции 



Пример
Граф
Рассмотрим простой связный ориентированный граф 
Он имеет матрицу смежности 

Найдём булевы степени этой матрицы 





Получим матрицу достижимости

Таким образом, из вершины 
При использовании же алгебраических операций получится матрица

Она показывает количество путей длины от 1 до 4 между вершинами орграфа.
Алгоритм Уоршелла
Существует другой алгоритм, позволяющий найти матрицу достижимости в точности за 
Связанные понятия
Матрица сильной связности
Матрица сильной связности простого орграфа — бинарная матрица, содержащая информацию обо всех сильно связанных вершинах в орграфе. Матрица сильной связности симметрична. У сильно связного графа такая матрица заполнена единицами.
Построение матрицы сильной связности
Матрица сильной связности может быть построена из матрицы достижимости. Пусть 



Пример
Рассмотрим тот же граф, что и ранее.
Его матрица достижимости:

Из неё получаем матрицу сильной связности:

Вершины 3 и 4 сильно связаны друг с другом и сами с собой.
Матрица связности графа
Для обычного (не ориентированного) связного графа существует понятие матрицы связности, сходное с матрицей достижимости.
Матрица контрдостижимости
Матрица контрдостижимости Q графа G может быть найдена из матрицы достижимости путем ее транспонирования.