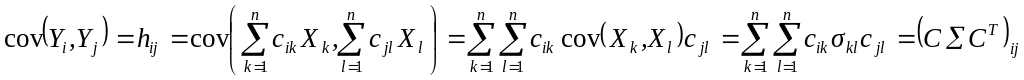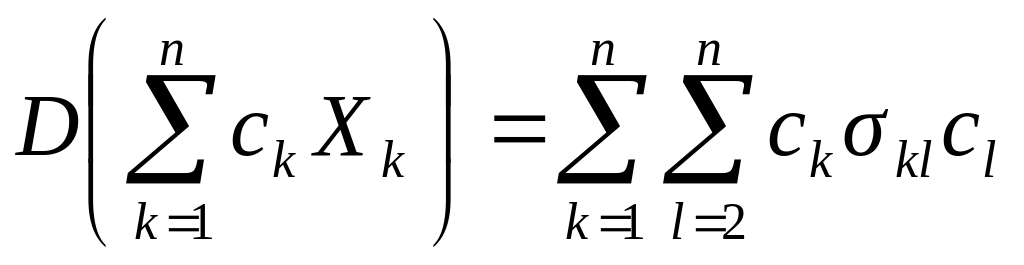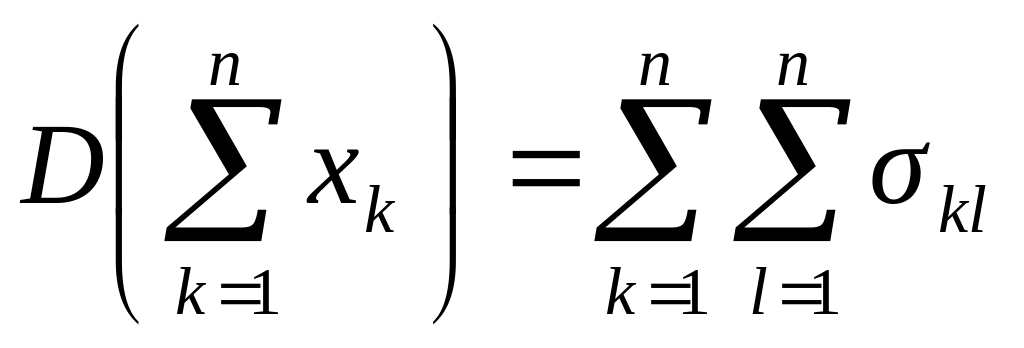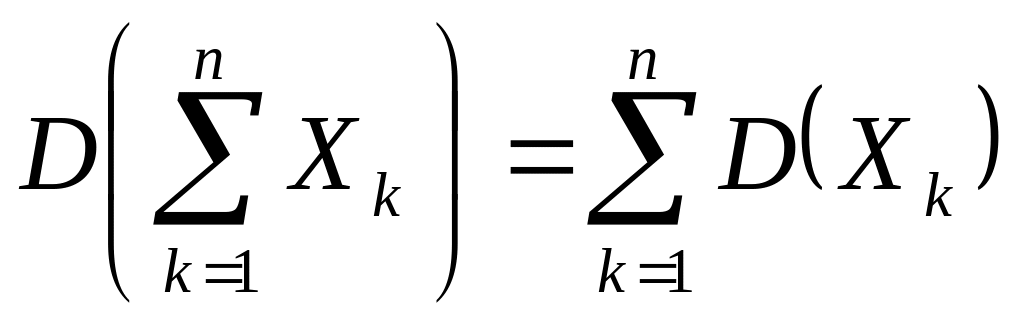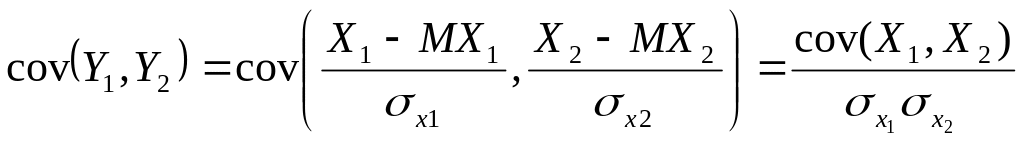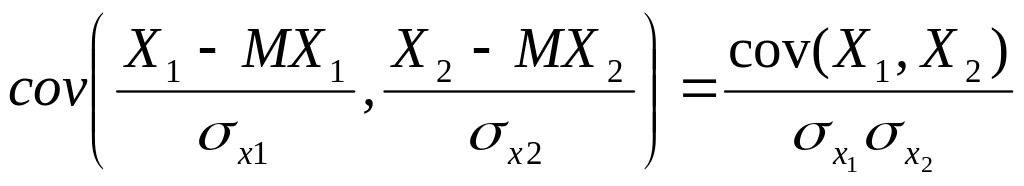Как найти матрицу ковариации

A covariance matrix is a type of matrix used to describe the covariance values between two items in a random vector. It is also known as the variance-covariance matrix because the variance of each element is represented along the matrix’s major diagonal and the covariance is represented among the non-diagonal elements. A covariance matrix is usually a square matrix. It is also positive semi-definite and symmetric. This matrix comes in handy when it comes to stochastic modeling and Principal component analysis.

What is Covariance Matrix?

The variance-covariance matrix is a square matrix with diagonal elements which represent the variance and the non-diagonal components that express covariance. The covariance of a variable can take any real value- positive, negative, or zero. A positive covariance suggests that the two variables have a positive relationship, whereas a negative covariance indicates that they do not. If two elements do not vary together, they have a zero covariance.

Covariance Matrix Example

Say there are 2 data sets X = [10, 5] and Y = [3, 9]. The variance of Set X = 12.5 and the variance of set Y = 18. The covariance between both variables is -15. The covariance matrix is as follows:

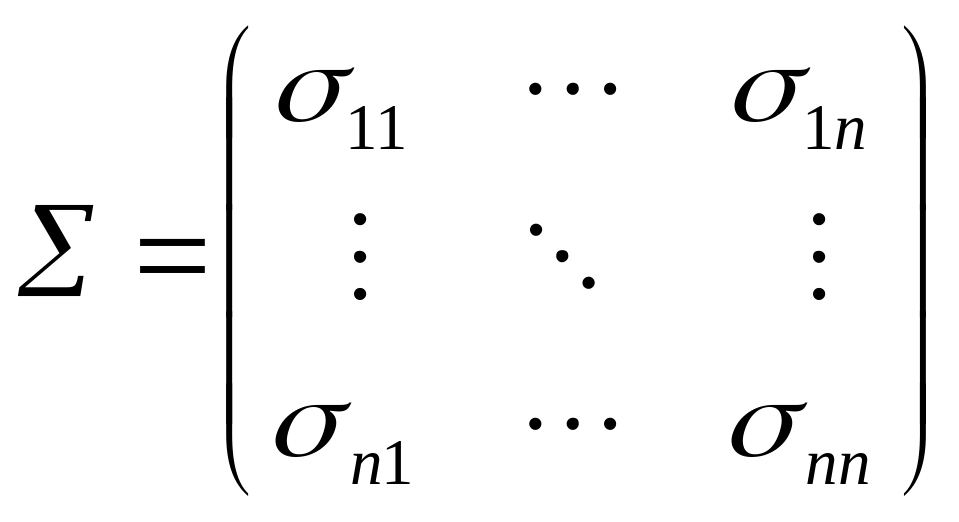
$begin{bmatrix} Variance~of~Set~X & Coorelation~of~Both~Sets\ Coorelation~of~Both~Sets& Variance~of~Set~Y end{bmatrix}=begin{bmatrix} 12.5 & -15\ -15& 18 end{bmatrix}$

Covariance Matrix Formula

The general form of a covariance matrix is given as follows:

$begin{bmatrix} Var(x_{1}) & &Cov(x_{1},x_{n})\ Cov(x_{n},x_{1}) & & Var(x_{n}) end{bmatrix}$

where,

How to find the Covariance Matrix?

The dimensions of a covariance matrix are determined by the number of variables in a given data set. If there are only two variables in a set, then the covariance matrix would have two rows and two columns. Similarly, if a data set has three variables, then its covariance matrix would have three rows and three columns.

The data pertains to marks scored by Anna, Caroline, and Laura in Psychology and History. Make a covariance matrix.

Student	Psychology(X)	History(Y)
Anna	80	70
Caroline	63	20
Laura	100	50

The following steps have to be followed:

Step 1: Find the mean of variable X. Sum up all the observations in variable X and divide the sum obtained with the number of terms. Thus, (80 + 63 + 100)/3 = 81.

Step 2: Subtract the mean from all observations. (80 – 81), (63 – 81), (100 – 81).

Step 3: Take the squares of the differences obtained above and then add them up. Thus, (80 – 81)² + (63 – 81)² + (100 – 81)².

Step 4: Find the variance of X by dividing the value obtained in Step 3 by 1 less than the total number of observations. var(X) = [(80 – 81)² + (63 – 81)² + (100 – 81)²] / (3 – 1) = 343.

Step 5: Similarly, repeat steps 1 to 4 to calculate the variance of Y. Var(Y) = 633.

Step 6: Choose a pair of variables.

Step 7: Subtract the mean of the first variable (X) from all observations; (80 – 81), (63 – 81), (100 – 81).

Step 8: Repeat the same for variable Y; (70 – 47), (20 – 47), (50 – 47).

Step 9: Multiply the corresponding terms: (80 – 81)(70 – 47), (63 – 81)(20 – 47), (100 – 81)(50 – 47).

Step 10: Find the covariance by adding these values and dividing them by (n – 1). Cov(X, Y) = (80 – 81)(70 – 47) + (63 – 81)(20 – 47) + (100 – 81)(50 – 47)/3-1 = 481.

Step 11: Use the general formula for the covariance matrix to arrange the terms. The matrix becomes: $begin{bmatrix} 343 & 481\ 481& 633 end{bmatrix}$

Properties of Covariance Matrix

A covariance matrix is always square, implying that the number of rows in a covariance matrix is always equal to the number of columns in it.
A covariance matrix is always symmetric, implying that the transpose of a covariance matrix is always equal to the original matrix.
A covariance matrix is always positive and semi-definite.
The eigenvalues of a covariance matrix are always real and non-negative.

Solved Examples on Covariance Matrix

Example 1: The marks scored by 3 students in Physics and Biology are given below:

Student	Physics(X)	Biology(Y)
A	92	80
B	60	30
C	100	70

Prepare the sample covariance matrix from the above data.

Solution:

Sample covariance matrix is given by $frac{sum_{1}^{n}left ( x_{i} -overline{x}right )^{2} }{n-1}$ .

Here, μ_x = 84, n = 3

var(x) = [(92 – 84)² + (60 – 84)² + (100 – 84)²] / (3 – 1) = 448

Also, μ_y = 60, n = 3

var(y) = [(80 – 60)² + (30 – 60)² + (70 – 60)²] / (3 – 1) = 700

Now, cov(x, y) = cov(y, x) = [(92 – 84)(80 – 60) + (60 – 84)(30 – 60) + (100 – 84)(70 – 60)] / (3 – 1) = 520.

The population covariance matrix is given as: $begin{bmatrix} 448 & 520\ 520& 700 end{bmatrix}$

Example 2. Prepare the population covariance matrix from the following table:

Age	Number of People
29	68
26	60
30	58
35	40

Solution:

Population variance is given by $frac{sum_{1}^{n}left ( x_{i} -muright )^{2} }{n}$ .

Here, μ_x = 56.5, n = 4

var(x) = [(68 – 56.5)² + (60 – 56.5)² + (58 – 56.5)² + (40 – 56.5)² ] / 4 = 104.75

Also, μ_y = 30, n = 4

var(y) = [(29 – 30)² + (26 – 30)² + (30 – 30)² + (35 – 30)²] / 4 = 10. 5

Now, cov(x, y) = $frac{sum_{1}^{4}left ( x_{i} -mu_{x}right )left ( y_{i}-mu_{y} right ) }{4}$

cov(x, y) = -27

The population covariance matrix is given as: $begin{bmatrix} 104.7 &-27 \ -27& 10.5 end{bmatrix}$

Example 3. Interpret the following covariance matrix:

$begin{bmatrix} & X & Y & Z\ X & 60 & 32 & -4\ Y & 32 & 30 & 0\ Z & -4 & 0 & 80 end{bmatrix}$

Solution:

The diagonal elements 60, 30, and 80 indicate the variance in data sets X, Y, and Z respectively. Y shows the lowest variance whereas Z displays the highest variance.

The covariance for X and Y is 32. As this is a positive number it means that when X increases (or decreases) Y also increases (or decreases)

The covariance for X and Z is -4. As it is a negative number it implies that when X increases Z decreases and vice-versa.

The covariance for Y and Z is 0. This means that there is no predictable relationship between the two data sets.

Example 4. Find the sample covariance matrix for the following data:

X	Y	Z
75	10.5	45
65	12.8	65
22	7.3	74
15	2.1	76
18	9.2	56

Solution:

Sample covariance matrix is given by $frac{sum_{1}^{n}left ( x_{i} -overline{x}right )^{2} }{n-1}$ .

n = 5, μ_x = 22.4, var(X) = 321.2 / (5 – 1) = 80.3

μ_y = 12.58, var(Y) = 132.148 / 4 = 33.037

μ_z = 64, var(Z) = 570 / 4 = 142.5

cov(X, Y) = $frac{sum_{1}^{5}left ( x_{i} -22.4right )left ( y_{i}-12.58right ) }{5-1} = -11.76$

cov(X, Z) = $frac{sum_{1}^{5}left ( x_{i} -22.4right )left ( z_{i}-64 right ) }{5-1} = 34.97$

cov(Y, Z) = $frac{sum_{1}^{5}left ( y_{i} -12.58right )left ( z_{i}-64 right ) }{5-1} = -40.87$

The covariance matrix is given as:

$begin{bmatrix} 80.3 & -13.865 &14.25 \ -13.865 & 33.037 & -39.5250\ 14.25 & -39.5250 & 142.5 end{bmatrix}$

FAQs on Covariance Matrix

Question 1: What is a covariance matrix?

Answer:

A covariance matrix is a type of matrix used to describe the covariance values between two items in a random vector.

Question 2: What is the general form of a 2 x 2 covariance matrix?

Answer:

The general form of a covariance matrix is given as follows:

$begin{bmatrix} Var(x_{1}) & &Cov(x_{1},x_{n})\ Cov(x_{n},x_{1}) & & Var(x_{n}) end{bmatrix}$

Question 3: Is the Variance Covariance Matrix Symmetric?

Answer:

Yes, the variance-covariance matrix is symmetric. It means that the transposition of a covariance matrix will result in the original matrix. In other words, M^T = M, where M is the covariance matrix.

Question 4: What are the Applications of the Covariance Matrix?

Answer:

The covariance matrix is commonly used in economics, financial engineering, and machine learning. The Cholesky decomposition performs a Monte Carlo simulation using the covariance matrix. This simulation is used to develop a variety of mathematical models.

Related Resources

Chance and Probability

Pie Chart

Graphical Representation of Data

Last Updated :
09 Jan, 2023

Like Article

Save Article

Источник

Между
случайными величинами может существовать
функциональная взаимосвязь. Однако
связь может быть и такого рода, что закон
распределения одной случайной величины
изменяется в зависимости от значений,
принимаемых другой случайной величиной.
Такую зависимость называют стохастической
или вероятностной. Одной из характеристик
стохастической взаимосвязи двух
случайных величин является ковариация
случайных величин.

Определение
1.
Ковариацией
случайных величин Х_i
и Х_j
называется число, равное математическому
ожиданию произведения отклонений
случайных величин Х_i
и X_j
от своих математических ожиданий

.
(1)

При
вычислении используется формула

.
(2)

Покажем
справедливость этого утверждения:

_ij=M((X_i
– MX_j)
(X_j
– MX_j))
= M(Х_i
Х_j
– X_i
MX_j
– MX_j
X_j+
MX_j
MX_j)
=M(Х_i
Х_j)
– MX_j
MX_j
– MX_j
MX_j
+ MX_j
MX_j
= M(Х_i
Х_j)
– MX_j
MX_j.

Если
Х_i
и Х_j
независимы, то ковариация равна нулю,
так как М(Х_i
, X_j)
= МХ_iМX_j.
Обратное утверждение неверно. Если
ковариация не равна нулю, то случайные
величины зависимы.

Рассмотрим
некоторые свойства ковариации:

1)
cov(X,
Y)
= cov(Y,
X);

2)
cov(X,
X)
= DX;

3)
cov(X
+
c,
Y
+
c)
= cov(X,
Y);

4)
cov(Xc₁
+ Yc₂,
Z)
= с₁cov(X,
Z)
+ с₂cov(Y,
Z),
с₁,
c₂
– const.

Пусть
задан случайный вектор X
=
(X₁,
X_2,…,X_n).

Определение
2. Ковариационной
матрицей случайного вектора X
= (X₁,
X_2,…,X_n)
назвается матрица ,
элементами которой являются ковариации

:

(3)

Очевидно,
что матрица симметричная, а диагональные
элементы равны дисперсиям случайных
величин Х_i,
_ii
= DX_i,
i
= 1,2,…

Определение
3. Определитель
ковариационной матрицы 
называется обобщенной
дисперсией
случайного вектора, который характеризует
меру рассеивания случайного n-мерного
вектора.

В
теории вероятностей и её приложениях
часто появляется необходимость перейти
с помощью линейного преобразования к
новым случайным величинам, X
=
(X₁,
X_2,

…,X_n)→
Y
= (Y₁,
Y_2,

…,Y_m),при
этом

.

Обозначим
через С
=
{c_ij}
матрицу коэффициентов линейного
преобразования, через Х
и
Y
– векторы столбцы
,
тогда линейное преобразование можно
записать как Y
= CX.

Теорема
1.
Если для случайного вектора Х
существует
ковариационная матрица Σ, то при любых
значениях элементов матрицы С
существует
ковариационная матрица Н
для случайного вектора Y
=
CX,
причём

.

Доказательство.
Пусть

;

;

Следствие
1.

.
(4)

Доказательство.
Пусть

.

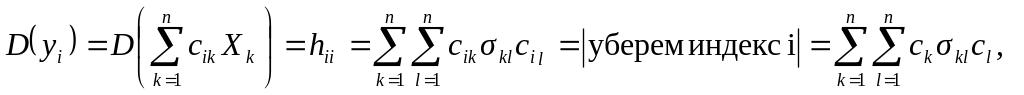
например,
если n
= 2, то

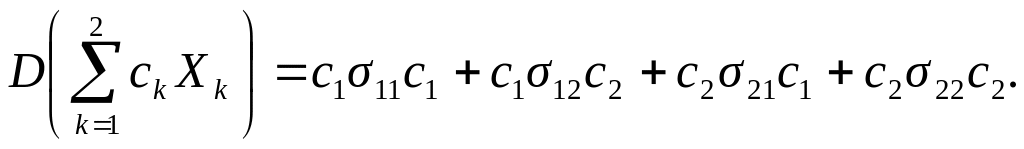
Следствие
2.
Если в формуле из следствия 1 предположить,
что

,
то

.
(5)

Следствие
3.
Если в формуле из следствия 1 предположить,
что n
=
1, то

Следствие
4.
Если в формуле из следствия 2 предположить,
что n
=
2, то

(6)

Следствие
5.
Если Х_k
независимы, то в матрице 
все недиагональные элементы равны нулю,
а диагональные элементы равны дисперсиям
соответствующих элементов Х_к,
поэтому, учитывая следствие 2, имеем

Пример
1.
Вычислим ковариационную матрицу 
случайного вектора Z
= (X,Y),
дисперсии случайных величин U₁
= X+Y,
U₂
= 2X–3Y
и ковариационную матрицу Н
вектора U
= (U₁,
U₂).
Распределение случайного вектора Z
задано в таблице.

	J	1	2	3	4	p_i_
I	Y_j X_i	0	0,1	0,2	0,3
1	5	0,2	0,1	0,05	0,05	0,4
2	6	0	0,15	0,15	0,15	0,1
3	7	0	0	0,1	0,1	0,2
p__j		0,2	0,25	0,3	0,25

МХ
= 5·0,4+6·0,4+7·0,2 = 5,8; М
Y
= 0·0,2+0,1·0,25+0,2·0,3+0,3·0,25 = 0,16;

М(Х,Y)=
5·0·0,2+5·0,1·0,1+5·0,05·0,2+5·0,05·0,3+6·0·0+6·0,1·0,1+6·0,15·0,2+6·0,1·0,3+7·0·0+7·0·0,1+7·0,1·0,2+7·0,1·0,3
= 0,975.

Матрица

имеет
вид
=
,
где
_11

=cov(X,X),
_12

=cov(X,Y),
_21

=cov(Y,X),
_22

=cov(Y,Y);

₁₂
= ₂₁=
M(XY)-MXMY
= 0,975-5,8·0,16 = 0,047;

₁₁
= cov(X,X)
= DX=MX²–
(MX)²
= (5²·0,4+6²·0,4+7²·0,2)
– 5,8²
= 0,56;

_22

=cov(Y,Y)
= DY
= MY²–
(MY)²
= (0·0,2+0,1²·0,25+0,2²·0,3+0,3²·0,25)
– 0,16²
= 0,0114.

Следовательно,

=

.

Найдем
DU₁
= D(X
+ Y)=

0,56
+ 0,047 + 0,047 + 0,0114 = 0,6654;

DU₂
= D(2X
– 3Y)
=

c₁₁₁c₁
+ c₁₁₂c₂
+ c₂₂₁c₁+
c₂₂₂c₂
= 2·2·0,56 – 2·3·0,047 – 3·2·0,047 + 3·3·0,0114 = 1,778.

Ковариационную
матрицу вектора U
= (U₁,
U₂)
можно определить по формуле

,
где С
=

,
тогда Н
=

.

Из
свойств ковариации следует, что значение
ковариации линейно зависит от масштаба
измерения случайных величин. Если
изменить масштаб, то изменится и значение
ковариации, например, если от случайной
величины Х₂
перейти к новой случайной величине Y₂=
с₂
Х₂,
то cov(X₁,
Y₂)
= c₂cov(X₁,X₂).
Это свойство ковариации ограничивает
возможности его применения. Для получения
характеристики взаимосвязи случайных
величин, которая бы не зависела от
преобразования случайных величин вида
Y
= аX
+ в,
перейдем к рассмотрению нормированных
случайных величин.

Пусть
Х₁,
Х₂
– случайные величины. Тогда им
соответствуют нормированные величины:

,

.

Найдем
ковариацию Y₁,Y₂

– коэффициент
корреляции случайных величин.

Определение
4. Коэффициентом
корреляции случайных величин Х₁,
Х₂
называется число _х1,

х2
равное ковариации нормированных
случайных величин Х₁,
Х₂,
т.е.

_х1,

х2
=
.

Для
независимых случайных величин _х1,х2
= 0, так как cov(X₁,X₂)
= 0. Обратное утверждение не верно (оно
справедливо только для нормально
распределенных случайных величин), но
если _х1,х2

0, то случайные величины Х₁,
Х₂
– зависимы.

Определение
5.
Случайные
величины называются некоррелированными,
если
_х1,

х2
= 0.

При
изменении масштаба случайной величины
значение корреляции не изменяется.

Рассмотрим
пример, который показывает, что из
равенства нулю коэффициента корреляции
не следует независимость случайных
величин.

Пусть

,
тогда

Теорема
2.
Абсолютное значение коэффициента
корреляции меньше либо равно 1:

Доказательство.
Пусть заданы случайные величины Х₁,
Х₂.
Рассмотрим нормированные случайные
величины

,

.
Тогда в соответствии с формулой (6)

следовательно,

Теорема
3.

,
тогда и только тогда, когда X_1,X₂связаны
линейной зависимостью, т.е. Х₂
= Х₁
+ ,
причем если 
> 0, то

;
если <
0, то

Доказательство.

Пусть

.
Покажем, что Х₁
и Х₂линейно
зависимы.

,
т.е.

Покажем,
что с = 0.

,
т.е.

,

следовательно

.
Запишем последнее равенство в виде

выразим
из него Х₂:

обозначив
множитель при первом слагаемом ,
а два других через ,
получим, что

Х₂
= Х₁
+ .

Аналогичный
результат можно получить в предположении,
что

II.
Пусть Х₂
= Х₁
+ ,
покажем, что

.

,

,
следовательно

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Время на прочтение
5 мин

Количество просмотров 42K

В первой части показано, как на основе матрицы расстояний между элементами получить матрицу Грина. Ее спектр образует собственную систему координат множества, центром которой является центроид набора. Во второй рассмотрены спектры простых геометрических наборов.

В данной статье покажем, что матрица Грина и матрица корреляции — суть одно и то же.

7. Векторизация и нормирование одномерных координат

Пусть значения некой характеристики элементов заданы рядом чисел . Для того, чтобы данный набор можно было сравнивать с другими характеристиками, необходимо его векторизовать и обезразмерить (нормировать).
Для векторизации находим центр (среднее) значений

и строим новый набор как разность между исходными числами и их центроидом (средним):

Получили вектор. Основной признак векторов состоит в том, что сумма их координат равна нулю. Далее нормируем вектор, — приведем сумму квадратов его координат к 1. Для выполнения данной операции нам нужно вычислить эту сумму (точнее среднее):

Теперь можно построить ССК исходного набора как совокупность собственного числа S и нормированных координат вектора:

Квадраты расстояний между точками исходного набора определяются как разности квадратов компонент собственного вектора, умноженные на собственное число. Обратим внимание на то, что собственное число S оказалось равно дисперсии исходного набора (7.3).

Итак, для любого набора чисел можно определить собственную систему координат, то есть выделить значение собственного числа (она же дисперсия) и рассчитать координаты собственного вектора путем векторизации и нормирования исходного набора чисел. Круто.

Упражнение для тех, кто любит «щупать руками». Построить ССК для набора {1, 2, 3, 4}.

Ответ.

Собственное число (дисперсия): 1.25.
Собственный вектор: {-1.342, -0.447, 0.447, 1.342}.

8. Векторизация и ортонормирование многомерных координат

Что, если вместо набора чисел нам задан набор векторов — пар, троек и прочих размерностей чисел. То есть точка (узел) задается не одной координатой, а несколькими. Как в этом случае построить ССК? Стандартный путь следующий.

Введем обозначение характеристик (компонент) набора. Нам заданы точки (элементы) и каждой точке соответствует числовое значение характеристики . Обращаем внимание, что второй индекс — это номер характеристики (столбцы матрицы), а первый индекс — номер точки (элемента) набора (строки матрицы).

Далее векторизуем характеристики. То есть для каждой находим центроид (среднее значение) и вычитаем его из значения характеристики:

Получили матрицу координат векторов (МКВ) .
Следующим шагом как будто бы надо вычислить дисперсию для каждой характеристики и их нормировать. Но хотя таким образом мы действительно получим нормированные векторы, нам-то нужно, чтобы эти векторы были независимыми, то есть ортонормированными. Операция нормирования не поворачивает вектора (а лишь меняет их длину), а нам нужно развернуть векторы перпендикулярно друг другу. Как это сделать?

Правильный (но пока бесполезный) ответ — рассчитать собственные вектора и числа (спектр). Бесполезный потому, что мы не построили матрицу, для которой можно считать спектр. Наша матрица координат векторов (МКВ) не является квадратной — для нее собственные числа не рассчитаешь. Соответственно, надо на основе МКВ построить некую квадратную матрицу. Это можно сделать умножением МКВ на саму себя (возвести в квадрат).

Но тут — внимание! Неквадратную матрицу можно возвести в квадрат двумя способами — умножением исходной на транспонированную. И наоборот — умножением транспонированной на исходную. Размерность и смысл двух полученных матриц — разный.

Умножая МКВ на транспонированную, мы получаем матрицу корреляции:

Из данного определения (есть и другие) следует, что элементы матрицы корреляции являются скалярными произведениями векторов (грамиан на векторах). Значения главной диагонали отражают квадрат длины данных векторов. Значения матрицы не нормированы (обычно их нормируют, но для наших целей этого не нужно). Размерность матрицы корреляции совпадает с количеством исходных точек (векторов).

Теперь переставим перемножаемые в (8.1) матрицы местами и получим матрицу ковариации (опять же опускаем множитель 1/(1-n), которым обычно нормируют значения ковариации):

Здесь результат выражен в характеристиках. Соответственно, размерность матрицы ковариации равна количеству исходных характеристик (компонент). Для двух характеристик матрица ковариации имеет размерность 2×2, для трех — 3×3 и т.д.

Почему важна размерность матриц корреляции и ковариации? Фишка в том, что поскольку матрицы корреляции и ковариации происходят из произведения одного и того же набора векторов, то они имеют один и тот же набор собственных чисел, один и тот же ранг (количество независимых размерностей) матрицы. Как правило, количество векторов (точек) намного превышает количество компонент. Поэтому о ранге матриц судят по размерности матрицы ковариации.

Диагональные элементы ковариации отражают дисперсию компонент. Как мы видели выше, дисперсия и собственные числа тесно связаны. Поэтому можно сказать, что в первом приближении собственные числа матрицы ковариации (а значит, и корреляции) равны диагональным элементам (а если межкомпонентная дисперсия отсутствует, то равны в любом приближении).

Если стоит задача найти просто спектр матриц (собственные числа), то удобнее ее решать для матрицы ковариации, поскольку, как правило, их размерность небольшая. Но если нам необходимо найти еще и собственные вектора (определить собственную систему координат) для исходного набора, то необходимо работать с матрицей корреляции, поскольку именно она отражает скалярное произведение векторов.

Отметим, что метод главных компонент как раз и состоит в расчете спектра матрицы ковариации/корреляции для заданного набора векторных данных. Найденные компоненты спектра располагаются вдоль главных осей эллипсоида данных. Из нашего рассмотрения это вытекает потому, что главные оси — это и есть те оси, дисперсия (разброс) данных по которым максимален, а значит, и максимально значение спектра.

Правда, могут быть и отрицательные дисперсии, и тогда аналогия с эллипсоидом уже не очевидна.

9. Матрица Грина — это матрица корреляции векторов

Рассмотрим теперь ситуацию, когда нам известен не набор чисел, характеризующих точки (элементы), а набор расстояний между точками (причем между всеми). Достаточно ли данной информации для определения ССК (собственной системы координат) набора?

Ответ дан в первой части — да, вполне. Здесь же мы покажем, что построенная по формуле (1.3′) матрица Грина и определенная выше матрица корреляции векторов (8.1) — это одна и та же матрица.

Как такое получилось? Сами в шоке. Чтобы в этом убедиться, надо подставить выражение для элемента матрицы квадратов расстояний

в формулу преобразования девиации:

Отметим, что среднее значение матрицы квадратов расстояний отражает дисперсию исходного набора (при условии, что расстояния в наборе — это сумма квадратов компонент):

Подставляя (9.1) и (9.3) в (9.2), после несложных сокращений приходим к выражению для матрицы корреляции (8.1):

Итак, матрица Грина и матрица корреляции векторов — суть одно и то же. Ранг матрицы корреляции совпадает с рангом матрицы ковариации (количеством характеристик — размерностью пространства). Это обстоятельство позволяет строить спектр и собственную систему координат для исходных точек на основе матрицы расстояний.

Для произвольной матрицы расстояний потенциальный ранг (количество измерений) на единицу меньше количества исходных векторов. Расчет спектра (собственной системы координат) позволяет определить основные (главные) компоненты, влияющие на расстояния между точками (векторами).

Таким образом можно строить собственные координаты элементов либо на основании их характеристик, либо на основании расстояний между ними. Например, можно определить собственные координаты городов по матрице расстояний между ними.

Источник

3.3. Математические ожидания и ковариации векторов и матриц

При работе с линейными моделями удобно представлять данные в виде векторов или матриц. Элементы некоторых векторов или матриц статистических линейных моделей являются случайными переменными. Определение случайной переменной было дано. Значение этой переменной зависит от случайного результата опыта.

В этой книге рассматривается такой тип векторов случайных переменных отклика, элементы которого могут быть коррелированы, а влияющие на них переменные являются контролируемыми и неслучайными. В конкретной линейной модели, влияющие на отклик переменные, имеют выбранные или полученные в результате расчёта детерминированные значения. Таким образом, в рассматриваемых линейных моделях имеются два вектора случайных переменных:

у= и e=.

Значения i-й переменной у_i (i=1, 2, …, n) отклика наблюдаются в результате проведения i-го опыта эксперимента, а значения переменной e_i случайной ошибки не наблюдаются, но могут оцениваться по наблюдаемым значениям переменной отклика и значениям влияющих на неё переменных.

При рассмотрении линейных моделей широко используются векторы и матрицы случайных переменных, поэтому в первую очередь для них необходимо обобщить идеи математического ожидания, ковариации и дисперсии.

Математические ожидания

Математическое ожидание вектора у размеров пх1 случайных переменных y₁, y₂, …, у_п определяется как вектор их ожидаемых значений:

Е(у)=Е===y, (3.3.1)

Ковариационная и корреляционная матрицы случайного вектора

В случае многомерной случайной величины (случайного вектора) характеристикой разброса ее составляющих и связей между ними является ковариационная матрица.

Ковариационная матрица определяется как математическое ожидание произведения центрированного случайного вектора на тот же, но транспонированный вектор:

где

Ковариационная матрица имеет вид

где по диагонали стоят дисперсии координат случайного вектора o_n=D_Xi, o₂₂=D_X2, о_кк = D_Xk, а остальные элементы представляют собой ковариации между координатами

Ковариационная матрица является симметрической матрицей, т.е.

Для примера рассмотрим ковариационную матрицу двумерного вектора

Аналогично получается ковариационная матрица для любого /^-мерного вектора.

Дисперсии координат можно представить в виде

где Gi,C2. 0? — средние квадратичные отклонения координат случайного вектора.

Коэффициентом корреляции называется, как известно, отношение ковариации к произведению средних квадратичных отклонений:

После нормирования по последнему соотношению членов ковариационной матрицы получают корреляционную матрицу

которая является симметрической и неотрицательно определенной.

Многомерным аналогом дисперсии случайной величины является обобщенная дисперсия, под которой понимается величина определителя ковариационной матрицы

Другой общей характеристикой степени разброса многомерной случайной величины является след ковариационной матрицы

где т — вектор-столбец математических ожиданий;

|Х| — определитель ковариационной матрицы X;

? -1 — обратная ковариационная матрица.

Матрица X -1 , обратная к матрице X размерности пх п, может быть получена различными способами. Одним из них является метод Жордана—Гаусса. В этом случае составляется матричное уравнение

где х — вектор-столбец переменных, число которых равно я; b — я-мерный вектор-столбец правых частей.

Умножим слева уравнение (6.21) на обратную матрицу ХГ 1 :

Так как произведение обратной матрицы на данную дает единичную матрицу Е, то

Если вместо b взять единичный вектор

то произведение X -1 -е_х дает первый столбец обратной матрицы. Если же взять второй единичный вектор

то произведение Е 1 е₂ дает первый столбец обратной матрицы и т.д. Таким образом, последовательно решая уравнения

методом Жордана—Гаусса, получаем все столбцы обратной матрицы.

Другой метод получения матрицы, обратной к матрице Е, связан с вычислением алгебраических дополнений A_tJ.= (/= 1, 2. п; j = 1, 2, . п) к элементам данной матрицы Е, подстановкой их вместо элементов матрицы Е и транспортированием такой матрицы:

Обратная матрица получается после деления элементов В на определитель матрицы Е:

Важной особенностью получения обратной матрицы в данном случае является то, что ковариационная матрица Е является слабо обусловленной. Это приводит к тому, что при обращении таких матриц могут возникать достаточно серьезные ошибки. Все это требует обеспечения необходимой точности вычислительного процесса или использования специальных методов при вычислении таких матриц.

Пример. Написать выражение плотности вероятности для нормально распределенной двумерной случайной величины v Х₂)

при условии, что математические ожидания, дисперсии и ковариации этих величин имеют следующие значения:

Решение. Обратную ковариационную матрицу для матрицы (6.19) можно получить, используя следующее выражение обратной матрицы к матрице X:

где А — определитель матрицы X.

А_и, Л₁₂, А₂₁, А₂₂ — алгебраические дополнения к соответствующим элементам матрицы X.

Тогда для матрицы ]г- ! получаем выражение

Так как а₁₂ = 01О2Р и °2i =a 2 a iP> а a i2 a 2i = cyfст|р, то Значит,

Функция плотности вероятности запишется в виде

Подставив исходные данные, получим следующее выражение для функции плотности вероятности

Корреляция, ковариация и девиация (часть 3)

В данной статье покажем, что матрица Грина и матрица корреляции — суть одно и то же.

7. Векторизация и нормирование одномерных координат

и строим новый набор как разность между исходными числами и их центроидом (средним):

Упражнение для тех, кто любит «щупать руками». Построить ССК для набора <1, 2, 3, 4>.

8. Векторизация и ортонормирование многомерных координат

Умножая МКВ на транспонированную, мы получаем матрицу корреляции:

Правда, могут быть и отрицательные дисперсии, и тогда аналогия с эллипсоидом уже не очевидна.

9. Матрица Грина — это матрица корреляции векторов

в формулу преобразования девиации:

Подставляя (9.1) и (9.3) в (9.2), после несложных сокращений приходим к выражению для матрицы корреляции (8.1):

Предварительная обработка для глубокого обучения: от матрицы ковариации к улучшению изображения

Автор: FreeCodeCapm Team
Дата записи

Целью этого поста является переход от основ предварительной обработки данных к современным методам, используемым в глубоком обучении. Моя точка зрения в том, что мы можем использовать код (например, python/numpy), чтобы лучше понять абстрактные математические представления. Думать, кодируя! ?

Мы начнем с базовых, но очень полезных концепций в науке о данных и машинном обучении/глубоко обучении, таких как дисперсию и ковариационные матрицы. Мы пойдем дальше к некоторым методам предварительной обработки, используемые для подачи изображений в нейронные сети. Мы постараемся получить более конкретные идеи, используя код, чтобы на самом деле посмотреть, что делает каждое уравнение.

Предварительная обработка Относится ко всем преобразованиям на необработанные данные, прежде чем он подается в изучение машины или алгоритма глубокого обучения. Например, обучение сверточной нейронной сети на необработанных изображениях, вероятно, приведет к плохой классификации спектаклей ( Pal & Sudeep, 2016 ). Предварительная обработка также важно ускорить обучение (например, методы центрирования и масштабирования, см. Lecun et al., 2012; см. 4.3 ).

Вот учебник этого урока:

1. Фон: В первой части мы получим некоторые напоминания о дисперсии и ковариации. Мы увидим, как генерировать и построить поддельные данные, чтобы лучше понять эти концепции.

2. Препроцессия: Во второй части мы увидим основы некоторых методов предварительной обработки, которые могут быть применены к любым видам данных – средняя нормализация , Стандартизация и Отбеливание Отказ

3. Отбеливание изображений: В третьей части мы будем использовать инструменты и концепции, полученные в 1. и 2. сделать особый вид отбеливания под названием Анализ нуля компонента (Zca). Его можно использовать для предварительной обработки изображений для глубокого обучения. Эта часть будет очень практичной и веселой ☃️!

Не стесняйтесь вилкой ноутбук, связанный с этим постом ! Например, проверьте фигуры матриц каждый раз, когда у вас возникнут сомнение.

1. История

А. Дисперсия и ковариация

Дисперсия переменной описывает, сколько значения распространяются. Ковариация – это мера, которая рассказывает количество зависимости между двумя переменными.

Положительная ковариация означает, что значения первой переменной велики, когда значения второго переменных также большие. Отрицательная ковариация означает противоположное: большие значения из одной переменной связаны с небольшими значениями другого.

Ковариационная стоимость зависит от масштаба переменной, поэтому его трудно проанализировать. Можно использовать коэффициент корреляции, который легче интерпретировать. Коэффициент корреляции – это просто нормализованная ковариация.

Ковариационная матрица представляет собой матрицу, которая суммирует отклонения и ковариации набора векторов, и он может рассказать много вещей о ваших переменных. Диагональ соответствует дисперсии каждого вектора:

Давайте просто проверим с формулой дисперсии:

с N Длина вектора, а X̄ среднее значение вектора. Например, дисперсия первого столбца вектора А является:

Это первая клетка нашей ковариационной матрицы. Второй элемент на диагонали соответствует дисперсии второго вектора столбца от А и так далее.

Примечание : векторы, извлеченные из матрицы А соответствовать столбцам А Отказ

Другие клетки соответствуют ковариации между двумя векторами столбец от А Отказ Например, ковариация между первым и третьим столбцом расположена в ковариационной матрице в качестве столбца 1 и строки 3 (или столбец 3 и строки 1).

Давайте проверим, что ковариация между первым и третьим колоннельным вектором А равно -2,67. Формула ковариации между двумя переменными Х и Y является:

Переменные Х и Y Первые и третий столбец векторы в последнем примере. Давайте разделим эту формулу, чтобы быть уверенным, что она Crystal Clear:

Символ суммы ( σ ) означает, что мы будем инаправлять на элементах векторов. Начнем с первого элемента ( i = 1 ) и рассчитайте первый элемент Х минус среднее значение вектора Х Отказ

2. Умножьте результат с первым элементом Y минус среднее значение вектора Y Отказ

3. Повторяйте процесс для каждого элемента векторов и рассчитайте сумму всех результатов.

4. Разделите количество элементов в векторе.

Давайте начнем с матрицы А :

Мы рассчитаем ковариацию между первым и третьим векторами столбец:

X̄ = 3 , ȳ = 4 и n = 3 Итак, у нас есть:

Ок, отлично! Это ценность ковариационной матрицы.

Теперь простой способ Отказ С Numpy, ковариационная матрица может быть рассчитана с помощью функции NP.cov Отказ

Стоит отметить Что если вы хотите Numpy использовать столбцы в качестве векторов, параметр Rowvar = false должен быть использован. Также смещение = правда делится на N а не по N-1 Отказ

Давайте сначала создадим массив:

Теперь мы рассчитаем ковариацию с помощью функции numpy:

Нахождение ковариационной матрицы с точечным продуктом

Есть еще один способ вычислить ковариационную матрицу А Отказ Вы можете центрировать А Около 0. Среднее значение вектора вычтено из каждого элемента вектора, чтобы иметь вектор со средним значением 0. Он умножается со своим собственным транспонированием и делится на количество наблюдений.

Давайте начнем с реализации, а затем мы попытаемся понять связь с предыдущим уравнением:

Давайте проверим это на нашей матрице А :

Мы в конечном итоге с тем же результатом, что и раньше.

Объяснение просто. Точечный продукт между двумя векторами можно выразить:

Это верно, это сумма продуктов каждого элемента векторов:

Если N это количество элементов в наших векторах, и что мы делимся по N :

Вы можете отметить, что это не слишком далеко от формулы ковариации, которую мы видели ранее:

Единственное отличие состоит в том, что в формуле ковариации мы вычитаем среднее значение вектора от каждого из его элементов. Вот почему нам нужно центрировать данные, прежде чем делать точечный продукт.

Теперь, если у нас есть матрица А точечный продукт между А И его транспонирование даст вам новую матрицу:

Это ковариация матрицы!

B. Визуализируйте данные и ковариационные матрицы

Чтобы получить больше понимания о ковариационной матрице и как это может быть полезно, мы создадим функцию для его визуализации вместе с двумя данными. Вы сможете увидеть связь между ковариационной матрицей и данными.

Эта функция рассчитает ковариационную матрицу, как мы видели выше. Он создаст два подлома – один для ковариационной матрицы и один для данных. HeatMap () Функция из Морской Используется для создания градиентов цвета – небольшие значения будут окрашены в светло-зеленых и больших значениях в темно-синем. Мы выбрали одну из наших цветов палитры, но вы можете предпочесть другие цвета. Данные представлены в виде ScatterPlot.

C. Имитация данных

Теперь, когда у нас есть функция сюжета, мы создадим некоторые случайные данные для визуализации того, что может сказать нам ковариационную матрицу. Начнем с некоторых данных, нарисованных из обычного распространения с функцией Numpy NP.RANDOM.NOMMAL () Отказ

Эта функция нуждается в среднем, стандартное отклонение и количество наблюдений распределения в качестве ввода. Мы создадим две случайные переменные 300 наблюдений со стандартным отклонением 1. Первым будет иметь среднее значение 1 и второе среднее значение 2. Если мы случайным образом рисовали два набора 300 наблюдений от нормального распределения, оба вектора будут некоррелирован.

Примечание 1 : Мы транспонируем данные с .T Потому что оригинальная форма – (2, 300) И мы хотим количества наблюдений, как строки (так с формой (300, 2) ).

Примечание 2 : Мы используем np.random.seed Функция для воспроизводимости. Такое же случайное число будет использоваться в следующий раз, когда мы запускаем ячейку.

Давайте проверим, как выглядит данные:

Приятно, у нас есть два колоночных вектора.

Теперь мы можем проверить, что распределения являются нормальными:

Мы видим, что распределения имеют эквивалентные стандартные отклонения, а разные средства (1 и 2). Так что именно то, о чем мы просили.

Теперь мы можем построить наш набор данных и его ковариационную матрицу с нашей функцией:

Мы видим на рассеянном рассеянии, что два размера некоррелированы. Обратите внимание, что у нас есть одно измерение со средним значением 1 (оси Y), а другая со средним количеством 2 (ось X).

Кроме того, ковариационная матрица показывает, что дисперсия каждой переменной очень большой (около 1), а ковариация колонн 1 и 2 очень маленькая (около 0). Поскольку мы гарантировали, что два вектора независимы, это согласовано. Противоположное не обязательно верно: ковариация 0 не гарантирует независимость (см. здесь ).

Теперь давайте построим зависимые данные, указав один столбец с другой.

Корреляция между двумя размерами видна на графике разброса. Мы видим, что линия может быть нарисована и используется для прогнозирования y от х и наоборот. Ковариационная матрица не диагональна (вне нулевых клеток вне диагонали). Это означает, что ковариация между размерами ненулена.

Замечательно! Теперь у нас есть все инструменты, чтобы увидеть различные методы предварительной обработки.

2. Предварительная обработка

А. Средняя нормализация

Средняя нормализация просто удаляет среднее из каждого наблюдения.

где X ‘ Является ли нормализованный набор данных Х это оригинальный набор данных, а X̅ это среднее значение Х Отказ

Средняя нормализация имеет влияние центрирования данных вокруг 0. Мы создадим функцию Центр () сделать это:

Давайте попробуем с матрицей B Мы создали ранее:

Первый участок показывает снова оригинальные данные B И второй сюжет показывает центрированные данные (посмотрите на масштаб).

B. Стандартизация или нормализация

Стандартизация используется для размещения всех функций в одинаковом масштабе. Каждое измерение с нулевым центром разделена на его стандартное отклонение.

где X ‘ это стандартизированный набор данных, Х Оригинальный набор данных X̅ это среднее значение Х , и Σ это стандартное отклонение Х Отказ

Давайте создадим другой набор данных с другой шкалой, чтобы убедиться, что он работает.

Мы видим, что масштабы х и y разные. Обратите внимание, что корреляция кажется меньше из-за различий в масштабах. Теперь давайте стандартизируем это:

Выглядит неплохо. Вы можете видеть, что масштабы одинаковы, и что набор данных сосредоточен в соответствии с обеими осями.

Теперь посмотрите на ковариационную матрицу. Вы можете видеть, что дисперсия каждой координаты – верхняя левая ячейка и нижняя правая клетка – равна 1.

Эта новая ковариационная матрица на самом деле является корреляционной матрицей. Коэффициент корреляции Пирсона между двумя переменными ( C1 и C2 ) составляет 0,54220151.

C. Отбеливание

Отбеливание, или сферирование, данные означает, что мы хотим преобразовать его, чтобы иметь ковариационную матрицу, которая является матрицей идентификатора – 1 в диагонали и 0 для других ячеек. Это называется отбеливание в отношении белого шума.

Вот более подробную информацию о матрице личности.

Отбеливание немного сложнее, чем другая предварительная обработка, но теперь у нас есть все инструменты, которые нам нужно сделать это. Это включает в себя следующие шаги:

Нулевой центр данных
Декорреляция данных
Rescale данные

Давайте снова возьмем C и попробуйте сделать эти шаги.

Нулевое центрирование

Это относится к нормализации ( 2. A ). Проверьте для получения подробной информации о Центр () функция.

На данный момент нам нужно декоррелировать наши данные. Интуитивно, это означает, что мы хотим повернуть данные до тех пор, пока больше нет корреляции. Посмотрите на следующее изображение, чтобы увидеть, что я имею в виду:

Левый участок показывает коррелированные данные. Например, если вы возьмете точку данных с большой х ценность, шансы состоят в том, что связанные y Также будет довольно большой.

Теперь возьмите все точки данных и выполните вращение (возможно, примерно на 45 градусов против часовой стрелки. Новые данные, нанесенные справа, больше не коррелируются. Вы можете видеть, что большие и маленькие y y значения связаны с тем же типом x ценности.

Вопрос в том, как мы можем найти правильное вращение, чтобы получить некоррелированные данные?

На самом деле, именно то, что делают собственные векторы ковариационной матрицы. Они указывают на направление, где распространение данных на его максимуме:

Собственные векторы ковариационной матрицы дают вам направление, которое максимизирует дисперсию. Направление зеленый Линия – это то, где дисперсия максимальная. Просто посмотрите на самую маленькую и крупнейшую точку, проецируемую на этой строке – распространение большой. Сравните это с проекцией на Оранжевый Линия – распространение очень мало.

Для получения более подробной информации о eigendecomposition, см. Это пост Отказ

Таким образом, мы можем декоррелировать данные, проецируя его с помощью собственных веществ. Это будет иметь эффект, чтобы применить необходимое вращение и удалить корреляции между размерами. Вот шаги:

Рассчитайте ковариационную матрицу
Рассчитайте собственные векторы ковариационной матрицы
Примените матрицу собственных векторов к данным – это применит вращение Давайте упаковывать это в функцию:

Давайте попробуем декоррелировать нашу нулевую матрицу C Чтобы увидеть это в действии:

Хороший! Это работает.

Мы можем видеть, что корреляция больше не здесь. Ковариационная матрица, теперь диагональная матрица, подтверждает, что ковариация между двумя измерениями равна 0.

3. Ссылка данных

Следующим шагом является масштабирование некоррелированной матрицы, чтобы получить ковариационную матрицу, соответствующую матрицу идентификатора. Для этого мы масштабируем наши декоррелированные данные, разделив каждое измерение квадратным корнем его соответствующего собственного значения.

Примечание : Мы добавляем небольшое значение (здесь 10 ^ -5), чтобы избежать разделения на 0.

Ура! Мы видим, что с ковариационной матрицей, что это все хорошо. У нас есть то, что выглядит как матрица личности – 1 по диагонали и 0 в других местах.

3. Отбеливание изображений

Мы увидим, как отбеливание может быть применено для предварительной обработки набора данных изображения. Для этого мы будем использовать статью Pal & Sudeep (2016) где они дают некоторые подробности о процессе. Эта методика предварительной обработки называется нулевой компонентной анализом (ZCA).

Проверьте газету, но вот тот результат, который они получили. Оригинальные изображения (слева) и изображения после ZCA (справа) отображаются.

Первые вещи в первую очередь. Мы загрузим изображения из CIFAR DataSet. Этот набор данных доступен из KERAS, и вы также можете скачать его здесь Отказ

Набор тренировок CIFAR10 DataSet содержит 50000 изображений. Форма X_train это (50000, 32, 32, 3) Отказ Каждое изображение составляет 32 пиксель на 32 пикселя, и каждый пиксель содержит 3 размера (R, G, B). Каждое значение является яркость соответствующего цвета от 0 до 255.

Мы начнем с выбора только подмножества изображений, скажем, 1000:

Так-то лучше. Теперь мы изменим массив, чтобы иметь плоские данные изображения с одним изображением на строку. Каждое изображение будет (1, 3072) потому что 32 х 32 х. Таким образом, массив, содержащий все изображения, будет (1000, 3072) :

Следующим шагом является возможность увидеть изображения. Функция imshow () От MatPlotlib ( DOC ) можно использовать для отображения изображений. Это нужны изображения с формой (m x n x 3), поэтому давайте создадим функцию, чтобы изменить изображения и иметь возможность визуализировать их из формы (1, 3072) Отказ

Например, давайте построим один из изображений, которые мы загрузили:

Теперь мы можем реализовать отбеливание изображений. Pal & Sudeep (2016) Опишите процесс:

1. Первым шагом является расписание изображений для получения диапазона [0, 1] путем разделения на 255 (максимальное значение пикселей).

Напомним, что формула для получения диапазона [0, 1]:

Но, здесь минимальное значение равно 0, так что это приводит к:

Среднее вычитание: per-pixel или per – изображение?

Хорошо, круто, диапазон наших ценностей пикселей составляет от 0 до 1. Следующий шаг:

2. Вычтите среднее от всех изображений.

Будьте осторожны здесь.

Один из способов сделать это – взять каждое изображение и удалить среднее значение этого изображения из каждого пикселя ( jarrett et al., 2009 ). Интуиция этого процесса состоит в том, что он центрирует пиксели каждого изображения около 0.

Еще один способ сделать это – взять каждый из 3072 пикселей, которые у нас есть (32 на 32 пикселя для R, G и B) для каждого изображения и вычтите среднее значение этого пикселя по всем изображениям. Это называется средним вычитанием Per-Pixel. На этот раз каждый пиксель будет сосредоточен вокруг 0 Согласно всем изображениям Отказ Когда вы будете кормить свою сеть с изображениями, каждый пиксель считается другой особенностью. С помощью среднего вычитания PER-PIXEL мы сосредоточили каждую функцию (пиксель) около 0. Этот метод обычно используется (например, wan et al., 2013 ).

Теперь мы сделаем среднее вычитание Per-Pixel с наших 1000 изображений. Наши данные организованы с этими размерами (изображения, пиксели) Отказ Это было (1000, 3072) Поскольку есть 1000 изображений с 32 х 32-х пикселями. Таким образом, средний пиксель может быть получен из первой оси:

Это дает 3072 значения, которые являются количеством средств – один на пиксель. Давайте посмотрим, какие значения у нас есть:

Это около 0,5, потому что мы уже нормализовались до диапазона [0, 1]. Тем не менее, нам все еще нужно удалить среднее из каждого пикселя:

Просто чтобы убедить себя, что это сработало, мы вычислим среднее значение первого пикселя. Будем надеяться, что это 0.

Это не совсем 0, но достаточно маленькое, что мы можем считать, что это сработало!

Теперь мы хотим рассчитать ковариационную матрицу с нулевыми центрированными данными. Как мы видели выше, мы можем рассчитать его с NP.cov () Функция от Numpy.

Пожалуйста, обратите внимание на Что наши переменные являются нашими разными изображениями. Это подразумевает, что переменные являются рядами матрицы Х Отказ Просто чтобы быть понятным, мы расскажем эту информацию о Numpy с параметром Rowvar = True Даже если это Правда По умолчанию (см. DOC ):

Теперь волшебная часть – Мы рассчитаем особые значения и векторы ковариационной матрицы и используем их, чтобы повернуть наш набор данных. Посмотрите на Мой пост О сингулярном разложении ценностей (SVD), если вам нужно больше деталей.

Примечание : Это может занять немного времени с большим количеством изображений, и поэтому мы используем только 1000. В статье они использовали 10000 изображений. Не стесняйтесь сравнивать результаты в соответствии с тем, сколько изображений вы используете:

В статье они использовали следующее уравнение:

с U левые сингулярные векторы и S Особое значения ковариации первоначального нормализованного набора данных изображений и Х Нормализованный набор данных. ε это гиперпараметр, называемый коэффициентом отбеливания. Diag (а) Соответствует матрицу с вектором А как диагональ и 0 во всех других клетках.

Мы постараемся реализовать это уравнение. Давайте начнем с проверки размеров SVD:

S это вектор, содержащий 1000 элементов (сингулярные значения). Diag (ы) Таким образом, будет иметь форму (1000, 1000) с S Как диагональ:

Проверьте эту часть:

Это также форма (1000, 1000) а также U и U ^ T Отказ Мы также видели, что Х имеет форму (1000, 3072) Отказ Форма X_ZCA Таким образом:

который соответствует форме исходного набора данных. Хороший.

Неожиданно! Если вы посмотрите на бумагу, это не тот результат, который они показывают. На самом деле, это потому, что мы не перекаливали пиксели, и есть отрицательные значения. Для этого мы можем вернуть его в диапазон [0, 1] с той же техникой, что и выше:

Ура! Замечательно! Похоже на изображение из бумаги. Как упоминалось ранее, они использовали 10000 изображений, а не 1000, как мы.

Чтобы увидеть различия в результатах в соответствии с количеством используемых изображений и эффект Hyper-Parameter ε Вот результаты для разных ценностей:

Результат отбеливания отличается в зависимости от количества изображений, которые мы используем, и значение Hyper-Parameter ε Отказ Изображение слева – это исходное изображение. В статье Pal & Sudeep (2016) Используются 10000 изображений и. Это соответствует нижнему левому изображению.

Я надеюсь, что вы нашли что-то интересное в этой статье, вы можете прочитать его на моем Блог с латексным для математики вместе с другими статьями.

Вы также можете вилить ноутбук Jupyter на Github здесь Отказ

What is Covariance Matrix?

Covariance Matrix Example

Covariance Matrix Formula

How to find the Covariance Matrix?

Properties of Covariance Matrix

Solved Examples on Covariance Matrix

FAQs on Covariance Matrix

Related Resources

7. Векторизация и нормирование одномерных координат

8. Векторизация и ортонормирование многомерных координат

9. Матрица Грина — это матрица корреляции векторов

Рекомендуемые материалы

Ковариационная и корреляционная матрицы случайного вектора

Корреляция, ковариация и девиация (часть 3)

7. Векторизация и нормирование одномерных координат

8. Векторизация и ортонормирование многомерных координат

9. Матрица Грина — это матрица корреляции векторов

Предварительная обработка для глубокого обучения: от матрицы ковариации к улучшению изображения

1. История

А. Дисперсия и ковариация

B. Визуализируйте данные и ковариационные матрицы

C. Имитация данных

2. Предварительная обработка

А. Средняя нормализация

B. Стандартизация или нормализация

C. Отбеливание

3. Отбеливание изображений

Рекомендации