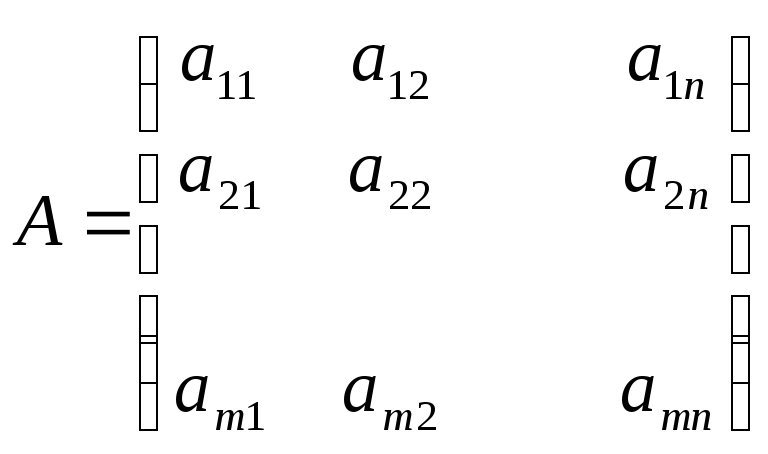Матрица линейного отображения
выберем базис в каждом пространстве
—
базис
—
базис
Каждому элементу пространства
сопоставляется один набор координат.
Рассмотрим образы всех базисных координат
Сопоставим матрицу A
число строк это размерность M, число столбцов это размерностьL

Матрица Аназывается матрицей
отображения в базисеeиg
Обозначение
Матрица линейного отображения: столбцы
матрицы линейного отображения – это
координатные столбцы образов базисных
векторов.
Пример
—
базис
Рассмотрим образы всех базисных векторов
4))
Изменение матрицы линейного отображения при смене базиса.
Пусть
—
базис и—
новый базис
— базис и
—
новый базис
Известна матрица отображения
Мы хотим найти
И известны матрицы перехода
и
§4
Инвариантные пространства
линейных операторов собственные числа
и собственные вектора.
1)
Определение:
Пусть есть линейный оператор Aкоторый действует вL
M– подпространство пространства
—
подпространство.
Пространство Mназывается инвариантным подпространством
оператораL, если
справедливо соотношение: образM
лежит вM.
Пример:
линейное пространство многочленов
оператор дифференцирования, тогда
инвариантным является подпространство
Теорема:
—
инвариантное подпространство оператораAэто условие равносильно
тому, что существует такой базис
пространстваL, в
Пусть
— базисLв котором
матрица имеет вид
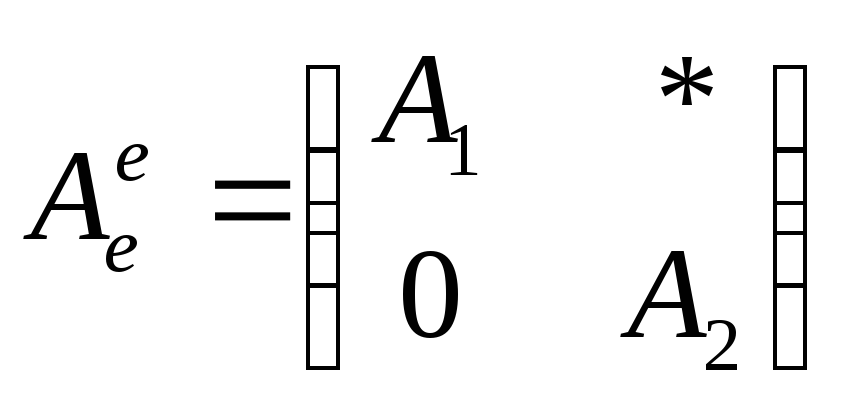
пространстваM
— базисM
Доказательство:
1)
— базисM
Любой линейно независимый набор можно
дополнить до базиса L:
—
базиси рассмотрим, как выглядит матрица
перехода в этом базисе.
следовательно
тогда матрица оператора
ч.т.д.
2) Следовательно в обратную сторону
Доказать, что есть пространство
M-размерностиrинвариантное относительно этого поля.
Возьмем.
— первые базисные вектора.
— их линейная оболочка
а) это линейная оболочка r– линейно независимых векторов
b) докажем, что оно
инвариантно: каждый образ элемента,
этого пространства лежит в пространстве.
т.е. образы всех базисов лежит в M
2))
Ядро и образ линейного оператора.
Определение:
,
тогда его ядром
это множество тех векторов пространства
L, которые операторомAпереводятся в 0.
Примеры
1)
2) А– проектирование пространствана плоскостиX0Y
Свойства ядра:
Лемма:ядро всякого оператора –
это инвариантное подпространство.
Доказательство.
1) Если
,
то их линейная комбинация так же лежит
в ядре. Рассмотрим
2) Образ ядра – это 0.
ч.т.д.
Определение:
Образ – это множество всех образов,
образ оператора A:ImA– это множество
всех векторов из пространстваL,
которые могут быть записаны как образы
Каши (?) либо элементов
ПримерДифферен.образ-
1)
2) оператора проектирования
Лемма:
Образ линейного оператора инвариантное
подпространство.
=
инвариантное подпространство
Доказательство:
1)
рассмотрим
Если 2 элемента лежат в образе, то их
линейная комбинация лежит в образе.
2) Докажем, что это подпространство
инвариантно.
3) Лемма:размерность ядра и образа
линейного оператора.
,
dim A=n,
тогда n=m+r
Доказательство.
Зафиксируем какой-нибудь базис
— базис
построим матрицу оператора в этом базисе
— матрица
среди векторов
;r –ЛНЗ следовательно
…
Вектора
порождают образы – это система образующих,
тогда в—r– ЛНЗ столбцов
следовательно.
рассмотрим ядро.
2)
Xe=0
=rang
rпространство
решенийn—r
системы размерность
эта размерность и есть размерность ядра
m=n—r
==
— базис каждому
y=Ax
ImAтогда
соответствует
—
это линейные комбинации столбцов матрицыА
3))
Матрица линейного отображения
Пусть — линейное отображение n-мерного пространства
в m-мерное пространство
. Зафиксируем в пространстве
произвольный базис
, а в пространстве
базис
. Линейное отображение однозначно задается образами базисных векторов (см. свойство 6). Разложим образы
, базисных векторов
по базису
Из координатных столбцов векторов относительно базиса
составим матрицу размеров
(9.1)
Она называется матрицей линейного отображения в базисах
и
. Матрицу отображения обозначают также
, чтобы подчеркнуть ее зависимость от выбранных базисов.
При помощи матрицы отображения найдем координаты образа по координатам прообраза
. Пусть
— координатный столбец вектора
, а
— координатный столбец вектора
, т.е.
и
. Тогда
В силу единственности разложения вектора по базису
получаем
Используя матричные операции, связь координат можно записать в виде
(9.2)
где — матрица (9.1) отображения
.
Таким образом, для каждого линейного отображения n-мерного пространства в m-мерное пространство
(с фиксированными базисами
и
соответственно) определена единственная матрица (9.1) этого отображения, и наоборот, любая числовая матрица размеров
является матрицей некоторого линейного отображения n-мерного пространства
в m-мерное пространство
.
Для нахождения матрицы отображения нужно выполнить следующие действия:
1) зафиксировать базисы и
пространств
и
2) найти образ первого базисного вектора и разложить его по базису
. Полученные координаты записать в первый столбец матрицы (9.1) отображения
;
3) найти образ второго базисного вектора и разложить его по базису
. Полученные координаты записать во второй столбец матрицы (9.1) отображения и т.д. В последний столбец матрицы (9.1) записать координаты образа
последнего базисного вектора.
Найдем матрицы отображений, рассмотренных выше.
1. Матрица нулевого отображения нулевая относительно любых базисов пространств
и
, так как образ любого базисного вектора равен нулевому вектору
, координаты которого равны нулю (относительно любого базиса пространства
).
2. Пусть в n-мерном линейном пространстве задан базис
. Рассмотрим отображение
, которое ставит в соответствие каждому вектору
его координатный столбец
относительно заданного базиса. В пространстве
выберем стандартный базис
. Напомним, что в стандартном базисе координатный столбец вектора
совпадает с самим столбцом
, так как
Поэтому образ первого базисного вектора
имеет координатный столбец
, совпадающий с первым базисным вектором
. Образ
и т.д. Составляя из этих столбцов матрицу отображения
, получаем единичную матрицу
n-го порядка.
3. В n-мерном евклидовом пространстве возьмем ортонормированный базис
. В качестве базиса одномерного линейного пространства
возьмем единицу. Рассмотрим отображение
, где
— алгебраическое значение проекции вектора
на направление, задаваемое вектором
. Тогда матрица отображения
имеет вид
, так как
, а
для
.
4. Взяв в пространствах и
стандартные базисы, находим образы базисных векторов (первые производные многочленов):
Записывая найденные координаты по столбцам матрицы отображения, получаем матрицу размеров
Свойства матриц линейных отображений
При фиксированных базисах линейных пространств:
1) матрица суммы линейных отображений равна сумме их матриц;
2) матрица произведения линейного отображения на число равна произведению матрицы отображения на то же самое число;
3) матрица обратного отображения является обратной для матрицы отображения;
4) матрица композиции отображений равна произведению матриц отображений:
.
Докажем, например, последнее свойство. Пусть в линейных пространствах фиксированы базисы
соответственно. Отображения
,
, а также их композиция
, имеют матрицы
относительно соответствующих базисов. Для координатных столбцов
векторов
запишем связи (9.2):
. Тогда
для координатного столбца
произвольного вектора
. Отсюда следует, что
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Определение 1. Пусть 














Пусть произвольный вектор 








Предложение 1. Существует взаимно однозначное отображение между множеством всех линейных отображений из 




Определение 2. Матрица линейного оператора2) — это матрица линейного отображения в случае, когда 
Пример 1. Пусть 






Предложение 2. Пусть 



Умножением двух линейных операторов 



Предложение 3. Пространство линейных операторов 






Содержание
Для понимания материалов настоящего раздела крайне желательно ознакомиться с разделом
ЛИНЕЙНОЕ ПРОСТРАНСТВО.
Линейное отображение
Линейным отображением линейного векторного пространства $ mathbb V_{} $ с операцией сложения векторов, обозначаемой $ +_{} $,
в линейное векторное пространство $ mathbb W_{} $ с операцией сложения векторов, обозначаемой $ boxplus_{} $,
называется функция (соответствие)
$$ mathcal A: mathbb V longmapsto mathbb W $$
(т.е. определенная на $ mathbb V_{} $, имеющая
значения в $ mathbb W_{} $), обладающая свойством линейности, которое описывается одним из двух эквивалентных представлений:
$$
mathcal A (X_1 +X_2)= mathcal A(X_1) boxplus mathcal A(X_2),quad mathcal A (alpha_1 X_1)=
alpha_1 mathcal A (X_1),
$$
или
$$
mathcal A(alpha_1 X_1 + alpha_2 X_2)= alpha_1 mathcal A(X_1) boxplus alpha_2 mathcal A(X_2)
$$
указанные свойства должны быть выполнены для любых векторов $ X_1,X_2 $ пространства $ mathbb V_{} $ и любых скаляров $ alpha_1,alpha_ 2 $ (вещественных если оба пространства
вещественны, и комплексных если хотя бы одно из пространств комплексное).
Если $ Y=mathcal A(X) $, то говорят, что $ Y_{} $ — образ вектора $ X_{} $, а $ X_{} $ —
прообраз вектора $ Y_{} $ при отображении $ mathcal A_{} $. Пространство $ mathbb V_{} $ называется областью определения отображения $ mathcal A_{} $.
Образно говоря, свойство линейности отображения заключается в том, что при этом отображении образ суммы любых двух векторов совпадает с суммой образов этих векторов, а произвольное растяжение прообраза влечет за собой сообразное же растяжение образа1).
Примеры линейных отображений
П
Пример 1. Рассмотрим линейное пространство
полиномов степени не выше $ n_{} $:
$$ mathbb P_n={p(x) in mathbb R[x] mid deg p(x) le n } , ; $$
в это же множество включаем и тождественно нулевой полином (для которого степень не определяется). Операция нахождения частного и операция нахождения остатка от деления полинома $ p(x)_{} $ на заданный фиксированный полином $ g(x) in mathbb R[x], g(x) notequiv 0 $ являются линейными отображениями пространства $ mathbb P_{n} $: если
$$ p_1(x)equiv q_1(x)g(x)+r_1(x), p_2(x)equiv q_2(x)g(x)+r_2(x) $$
при $ deg r_j(x)<deg g(x) $
то
$$
(alpha_1p_1(x)+alpha_2p_2(x)) equiv
$$
$$
equiv
(alpha_1q_1(x)+alpha_2q_2(x)) g(x) + (alpha_1r_1(x)+alpha_2r_2(x)) . $$
Фактически, операция деления на $ g_{}(x) $ (с остатком) порождает два разных линейных отображения. Если $ deg g(x) = m $ при $ 0<mle n $, то операция нахождения остатка — это отображение $ mathbb P_{n} mapsto mathbb P_{m-1} $, а операция нахождения частного — это отображение $ mathbb P_{n} mapsto mathbb P_{n-m} $.
П
Пример 2. В том же линейном пространстве $ mathbb P_{n}^{} $ операция дифференцирования
$$ frac{d }{d, x}: p(x) {color{Red}{ longmapsto} } p'(x) $$
является отображением $ mathbb P_{n}^{} $ в $ mathbb P_{n-1}^{} $ линейным
поскольку
$$frac{d }{d, x} (alpha_1 p_1(x) + alpha_2 p_2(x))=
alpha_1 frac{d }{d, x} p_1(x) + alpha_2 frac{d }{d, x} p_2(x)
.
$$
Прообраз любого элемента $ mathbb P_{n-1}^{} $ неединствен:
$ frac{d }{d, x}(frac{1}{2} x^2 + const)=x $.
П
Пример 3. Операцию нахождения первообразной:
$$
int_{0}^{x}:
begin{array}{ccc}
p(x) & {color{Red}{ longmapsto} } & int_{0}^{x} p(t) d, t \
a_0x^n+a_1x^{n-1}+cdots+a_n & {color{Red}{ longmapsto} } &
displaystyle frac{a_0}{n+1}x^{n+1}+frac{a_1}{n}x^{n}+cdots+a_nx
end{array}
$$
тоже можно рассматривать как линейное отображение
$ mathbb P_n {color{Red}{ longmapsto} } mathbb P_{n+1} $. При этом прообраз каждого полинома из
$ mathbb P_{n+1} $ (если существует) будет единствен.
П
Пример 4. Линейная форма от переменных $ x_{1},dots,x_n $:
$$mathcal A(x_1,dots,x_n)=a_1x_1+dots+a_nx_n,quad {a_j }_{j=1}^{n}
subset mathbb R $$
является примером линейного отображения $ mathbb R^{n}_{} $ в $ mathbb R_{} $. Здесь тоже
прообразов у одного и того же элемента из $ mathbb W_{} $ может быть несколько:
$$mathcal A(x_1,x_2)=2x_1-x_2 mbox{ отображает вектора } X_1=[0,0]
mbox{ и } X_2=[1,2] mbox{ в } 0 .$$
П
Пример 5. Обобщением предыдущего примера является
отображение $ mathcal A: mathbb R^n longmapsto mathbb R^m $, задаваемое
$$
mathcal A
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)
= left(begin{array}{c}
a_{11}x_1+a_{12}x_2 + cdots + a_{1n}x_n \
dots \
a_{m1}x_1+a_{m2}x_2 + cdots + a_{mn}x_n
end{array}
right)=
$$
$$
=
left(begin{array}{cccc}
a_{11} & a_{12}& dots & a_{1n} \
dots & & & dots \
a_{m1} & a_{m2}& dots & a_{mn}
end{array}
right) cdot
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)
$$
при произвольной вещественной матрице. Оно является линейным — в отличие от похожего на него отображения
$$
begin{array}{ll}
tilde{mathcal A}
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)
&= left(begin{array}{c}
a_{11}x_1+a_{12}x_2 + cdots + a_{1n}x_n +b_1 \
dots \
a_{m1}x_1+a_{m2}x_2 + cdots + a_{mn}x_n + b_m
end{array}
right)= \
&=left(begin{array}{cccc}
a_{11} & a_{12}& dots & a_{1n} \
dots & & & dots \
a_{m1} & a_{m2}& dots & a_{mn}
end{array}
right) cdot
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)+
left(begin{array}{c}
b_1 \ vdots \ b_m
end{array}
right)
end{array}
$$
при хотя бы одном из чисел $ b_1,dots,b_{m} $ отличном от нуля. В самом деле, если записать последнее в матричном виде:
$$
tilde{mathcal A}(X)=Acdot X+ mathcal B,
$$
то
$$
tilde{mathcal A}(alpha X)=Acdot (alpha X)+ mathcal B ne alpha tilde{mathcal A}(X)=
alpha left(Acdot X+ mathcal B right).
$$
Для этого отображения свойство линейности не выполняется. Для отображений такого типа приходится расширять множество линейных отображений: см.
☟
AФФИННОЕ ОТОБРАЖЕНИЕ.
П
Пример 6. Предыдущим примерам
можно дать и геометрическую интерпретацию. Так, линейное отображение $ mathbb R^3 longmapsto mathbb R^3 $:
$$left(begin{array}{c}
x \ y \ z
end{array}
right) longmapsto
left(begin{array}{c}
x \ y \ 0
end{array}
right)
$$
задает ортогональную проекцию вектора $ X=(x,y,z) $ на плоcкость $ z=0 $.
Можно рассматривать его и как отображение $ mathbb R^{3} longmapsto mathbb R^2 $.
Проецирование же на произвольное подпространство может быть задано
с помощью матрицы. Так, например, отображение
$$left(begin{array}{c}
x \ y \ z
end{array}
right) longmapsto
frac{1}{3} left(begin{array}{rrr}
2 & -1 & -1 \
-1& 2 & -1 \
-1 & -1 & 2
end{array}
right)
left(begin{array}{c}
x \ y \ z
end{array}
right)
$$
задает ортогональную проекцию вектора $ X_{} $ на многообразие $ x+y+z=0 $.
Общее выражение для отображения ортогонального проецирования на линейное подпространство в $ mathbb R^{n}_{} $
☞
ЗДЕСЬ.
П
Пример 7. В линейном пространстве $ mathbb R^{mtimes n} $ матриц порядка $ mtimes n_{} $ с вещественными элементами определим два отображения:
$$ X mapsto Acdot X quad u quad X mapsto X cdot B $$
умножения слева на фиксированную матрицу $ A_{elltimes m} $ и умножения справа на также фиксированную матрицу $ B_{ntimes k} $.
Оба отображения являются линейными. Линейным также будет и отображение
$$ X mapsto Acdot X cdot B . $$
При дополнительных условиях $ m=n=ell=k $ линейным будет и отображение
$$ X mapsto Acdot X + X cdot B . $$
Оно отображает пространство $ mathbb R^{ntimes n} $ в себя.
П
Пример 8. В пространстве полиномов с вещественными коэффициентами от $ m_{} $ переменных $ x_1,x_2,dots,x_{m} $ степени не выше $ n_{} $ рассмотрим отображение
$$ f(x_1,x_2,dots,x_m) mapsto operatorname{grad} (f)= left(frac{partial f}{partial x_1}, frac{partial f}{partial x_2}, dots, frac{partial f}{partial x_m}
right) .
$$
Здесь вектор $ operatorname{grad} (f) $ называется градиентом функции $ f_{} $. Это отображение будет линейным. Для его записи используют следующий формализм. Вводят в рассмотрение специальный вектор, называемый набла2)
$$ nabla = left(frac{partial }{partial x_1}, frac{partial }{partial x_2}, dots, frac{partial }{partial x_m} right) . $$
Умножение этого вектора на функцию $ f_{} $ имеет результатом именно градиент:
$$ nabla cdot f = operatorname{grad} (f) . $$
Умножение же этого вектора по правилу скалярного произведения на вектор $ F= (f_1,f_2,dots,f_m) $,
состоящий из $ m_{} $ полиномов, порождает отображение этого вектора в полином:
$$ operatorname{div} (F) = langle nabla, F rangle =frac{partial f_1 }{partial x_1}+ frac{partial f_2 }{partial x_2}+ dots+ frac{partial f_m }{partial x_m} ; $$
он называется дивергенцией вектора $ F_{} $. Это отображение
$$ F mapsto operatorname{div} (F) $$
также будет линейным.
?
В частном случае линейных форм:
$$ f_j=a_{j1}x_1+dots+a_{jn}x_m quad npu quad jin{1,dots,m} $$
получим связь $ operatorname{div} (F) $ с одним объектом матричного анализа. Каким именно?
?
Является ли линейным отображение
$$ X longmapsto operatorname{Sp} (X) , $$
определенное в пространстве квадратных матриц порядка $ n_{} $? Здесь $ operatorname{Sp} (X) $ — след матрицы $ X_{} $.
?
Про линейное отображение $ mathcal A $ пространства $ mathbb R^{3}_{} $ в пространство $ mathbb P_3^{} $ известно, что
$$ mathcal A(1,0,1)=1+3,x+x^3, mathcal A(1,-1,0)=-1+x-x^2 . $$
Найти $ mathcal A(-1,2,1) $.
Свойства линейных отображений
§
В настоящем пункте $ mathbb O_{} $ означает нулевой вектор пространства $ mathbb V_{} $,
а $ mathbb O’ $ — нулевой вектор пространства $ mathbb W_{} $.
Два линейных отображения $ mathcal A $ и $ mathcal B $ из
$ mathbb V_{} $ в $ mathbb W_{} $ называются равными если $ mathcal A(X)=mathcal B(X) $ для любого
$ Xin mathbb V $. Нулевое отображение определяется условием
$${mathcal O}(X)=mathbb O’ quad npu quad forall Xin mathbb V .$$
Т
Теорема 1. Для любого линейного отображения $ mathcal A(X) $:
а) $ mathcal A(mathbb O)=mathbb O’ $;
б) если система $ {X_1,dots,X_k} $ линейно зависима, то и система $ { mathcal A(X_1),dots,mathcal A(X_k) } $ линейно зависима;
в) если система $ { mathcal A(X_1),dots,mathcal A(X_k) } $ линейно независима, то и система
$ {X_1,dots,X_k} $ линейно независима.
Т
Теорема 2. Линейное отображение отображает произвольное линейное многообразие пространства $ mathbb V_{} $ в линейное же многообразие пространства $ mathbb W_{} $.
Доказательство. Если
$$ mathbb M = X_0+mathcal L(X_1,dots,X_k)=
$$
$$
={X_0+alpha_1X_1+dots+ alpha_kX_k mid (alpha_1,dots,alpha_k)in mathbb R^k } ,
$$
то свойство линейности отображения $ mathcal A_{} $ дает:
$$
mathcal A( mathbb M) ={mathcal A(X_0)boxplus alpha_1mathcal A(X_1) boxplus dots boxplus alpha_kmathcal A(X_k) mid (alpha_1,dots,alpha_k)in mathbb R^k } =
$$
$$
=mathcal A(X_0) boxplus mathcal L(mathcal A(X_1),dots,mathcal A(X_k)) .
$$
Заметим, что в соответствии с теоремой 1, можно утверждать, что линейное отображение не увеличивает размерности отображаемого многообразия: $ dim mathcal A( mathbb M) le dim mathbb M $.
♦
=>
Линейное отображение отображает произвольную прямую пространства $ mathbb V_{} $ в прямую или точку пространства $ mathbb W $.
?
Доказать, что линейное отображение отображает параллельные многообразия пространства $ mathbb V_{} $ в параллельные же многообразия пространства $ mathbb W_{} $.
Т
Теорема 3. Пусть $ {X_1,dots,X_n} $ — произвольный базис $ mathbb V_{} $,
а $ Y_1,dots,Y_n $ — произвольные векторы из $ mathbb W_{} $. Существует единственное линейное отображение $ mathcal A: mathbb V longmapsto mathbb W $ такое, что$$ mathcal A(X_1)=Y_1,dots,mathcal A(X_n)=Y_n .$$
Иными словами: любое линейное отображение пространства $ mathbb V_{} $ в другое пространство однозначно определяется его заданием на базисных векторах пространства $ mathbb V_{} $.
Доказательство. Поскольку векторы $ X_1,dots,X_{n} $ — базисные, то существует
и единственно разложение любого $ Xin mathbb V_{} $: $ X=x_1X_1+cdots+x_nX_n $.
Зададим отображение $ mathcal A: mathbb V longmapsto mathbb W $ формулой
$$mathcal A(X) = x_1Y_1boxplus dots boxplus x_nY_n . $$
Легко проверить свойство его линейности. Кроме того:
$$mathcal A(X_j)=mathcal A(0cdot X_1+dots+1cdot X_j+dots+0cdot X_n)=
$$
$$
=0cdot Y_1 boxplus dots boxplus 1cdot Y_j boxplus dots boxplus 0cdot Y_n=Y_j,$$
т.е. оно удовлетворяет условиям теоремы.
Предположим теперь, что существует еще одно отображение $ mathcal B(X) $,
удовлетворяющее этим условиям: $ mathcal B(X_j)=Y_j $. Тогда
$$mathcal A(X)=x_1Y_1 boxplus cdots boxplus x_nY_n=
$$
$$
=x_1mathcal B(X_1) boxplus cdots boxplus x_nmathcal B(X_n)=mathcal B(X),$$
и, на основании определения, $ mathcal A(X)=mathcal B(X) $.
♦
Отображение $ {mathcal S}: mathbb V longmapsto mathbb W $ называется
суммой линейных отображений $ mathcal A $ и $ mathcal B $ если
$ mathcal S(X)=mathcal A(X) boxplus mathcal B(X) $ для $ forall Xin mathbb V_{} $. Отображение
$ mathcal F:mathbb V longmapsto mathbb W $ называется
произведением линейного отображения $ mathcal A_{} $ на число (скаляр)
$ lambda_{} in mathbb R $ если $ {mathcal F}(X)=lambda cdot mathcal A(X) $ для $ forall Xin mathbb V_{} $.
Т
Теорема 4. Отображения $ {mathcal S} $ и $ {mathcal F} $ — линейные.
П
Пример. В пространстве полиномов $ mathbb P_n $
операцию нахождения второй производной
$$ frac{d^2 }{d, x^2}:p(x) longmapsto p»(x)$$
тоже можно рассматривать как линейное отображение $ mathbb P_n longmapsto mathbb P_{n-1} $.
Линейным также будет и отображение
$$ frac{d^2 }{d, x^2}times Box + 2 frac{d}{d, x}times Box: p(x)
longmapsto p»(x)+2 p'(x) .$$
Т
Теорема 5. Множество $ {mathcal H}om(mathbb V,mathbb W) $ всех линейных
отображений из $ mathbb V_{} $ в $ mathbb W_{} $ образует линейное пространство и$$dim {mathcal H}om(mathbb V,mathbb W) = dim mathbb V cdot dim mathbb W .$$
Ядро и образ линейного отображения
Для линейного отображения $ mathcal A $ его ядром3) называется множество векторов из $ mathbb V_{} $, отображающихся в
$ mathbb O’ in mathbb W $:
$$mathcal{K}er (mathcal A)= left{Xin mathbb V big| mathcal A(X)=mathbb O’ right} ; $$
а его образом называется множество всех векторов из
$ mathbb W_{} $, для каждого из которых существует прообраз из $ mathbb V_{} $:
$$mathcal{I}m (mathcal A)= left{Yin mathbb W mid exists X in mathbb V, mathcal A(X)= Y
right} .$$
Фактически $ mathcal{I}m (mathcal A) $ можно назвать областью значений линейного отображения $ mathcal A_{} $.
Т
Теорема 1. $ mathcal{K}er (mathcal A) $ и $ mathcal{I}m(mathcal A) $ являются
линейными подпространствами соответствующих пространств.
Для линейного отображения $ mathcal A_{} $ его дефектом называется размерность ядра,
а его рангом — размерность образа:
$$ operatorname{dfc}(mathcal A )=dim (mathcal{K}er (mathcal A )) ,
operatorname{rank}(mathcal A )= dim (mathcal{I}m (mathcal A )) .
$$
Отображение называется невырожденным если $ operatorname{dfc}(mathcal A )=0 $.
Т
Теорема 2. Линейное отображение $ mathcal A $ невырождено тогда и только тогда, когда у каждого образа существует единственный прообраз.
Доказательство. Необходимость. Если $ mathcal A $ невырождено, то $ mathcal{K}er (mathcal A )={mathbb O} $, т.е. единственным вектором из $ mathbb V_{} $, отображающимся в $ mathbb O’ in mathbb W $ должен быть $ mathbb O_{} $. Если предположить неединственность прообраза для какого-то
$ Yin mathbb W $: $ Y=mathcal A (X_1)=mathcal A (X_2) $ при $ X_1ne X_2 $, то
$$mathbb O’=mathcal A (X_1)-mathcal A (X_2)=mathcal A (X_1-X_2)$$
и получаем противоречие с единственностью прообраза у $ mathbb O’ $.
Достаточность. Пусть $ mathcal A (X_1)ne mathcal A (X_2) $ для любых $ X_1ne X_2 $. Если бы $ mathcal{K}er (mathcal A ) $ имело ненулевую размерность, то существовал бы $ Xne mathbb O $ такой, что $ mathcal A (X)=mathbb O’ $, что противоречило бы предыдущей фразе: $ mathcal A (X)= mathcal A (mathbb O) $.
♦
Т
Теорема 3. Если $ {X_1,dots,X_{n}} $ — произвольный базис $ mathbb V_{} $,
то $ mathcal{I}m (mathcal A) $ совпадает с линейной оболочкой образов этих векторов$$ mathcal{I}m (mathcal A) ={mathcal L}left(mathcal A (X_1),dots, mathcal A (X_n) right) .$$
Доказательство. Действительно, любой вектор $ Y in mathcal{I}m (mathcal A) $ является
образом какого-то вектора $ X=x_1X_1+cdots+x_nX_n $, тогда на основании
линейности отображения:
$$ Y=mathcal A (X)=x_1mathcal A (X_1) boxplus cdots boxplus x_n mathcal A (X_n) in
{mathcal L}left(mathcal A (X_1),dots, mathcal A(X_n) right) .$$
Таким образом
$$mathcal{I}m (mathcal A) subset
{mathcal L}left(mathcal A (X_1),dots, mathcal A (X_n) right) .$$
Обратно, поскольку векторы $ mathcal A (X_1),dots, mathcal A (X_n) $ принадлежат
$ mathcal{I}m (mathcal A) $, то по теореме 1 и любая линейная комбинация
этих векторов должна принадлежать $ mathcal{I}m (mathcal A) $:
$${mathcal L}left(mathcal A (X_1),dots, mathcal A (X_n) right)
subset mathcal{I}m (mathcal A) .$$
Из двух взаимных включений множеств следует их равенство.
♦
П
Пример. Найти ядро и образ отображения $ mathbb R^3 longmapsto mathbb R^4 $
$$
mathcal A left(begin{array}{c}
x_1 \ x_2 \ x_3
end{array}
right)=
left(begin{array}{c}
x_3 \ 0 \x_1+x_2+x_3 \ x_1+x_2-x_3
end{array}
right) .
$$
Решение. Для определения $ mathcal{K}er (mathcal A) $ найдем фундаментальную
систему решений системы уравнений
$$left{ begin{array}{rrr}
x_3 &=&0 \
0 &=&0 \
x_1+x_2+x_3 &=&0 \
x_1+x_2-x_3 &=&0
end{array} right. quad Longrightarrow
X_1= left(begin{array}{r}
-1 \ 1 \0
end{array}
right)
$$
Имеем $ operatorname{dfc}(mathcal A )=1 $ и $ mathcal{K}er (mathcal A)= mathcal L (X_1) $.
Теперь для нахождения $ mathcal{I}m (mathcal A) $ воспользуемся теоремой 3:
базис следует искать среди векторов
$$Y_1=mathcal A left(begin{array}{c}
1 \ 0 \0
end{array}
right)= left(begin{array}{c}
0 \ 0 \ 1 \ 1
end{array}
right),
Y_2=mathcal A left(begin{array}{c}
0 \ 1 \0
end{array}
right)= left(begin{array}{c}
0 \ 0 \ 1 \ 1
end{array}
right),
$$
$$
Y_3=mathcal A left(begin{array}{c}
0 \ 0 \1
end{array}
right)= left(begin{array}{r}
1 \ 0 \ 1 \ -1
end{array}
right) .
$$
Имеем: $ operatorname{rank}(mathcal A )=2 $ и $ mathcal{I}m (mathcal A) = mathcal L (Y_1,Y_3) $.
♦
П
Пример. Найти ядро и образ отображения пространства полиномов $ mathbb P_3 $ в $ mathbb P_2 $, задаваемого формулой:
$$ mathcal A left(p(x)right) = x^2 p^{prime prime} (x) + p^{prime} (x) — 6, p(x) . $$
Решение. Для начала проверим, что это отображение именно $ mathbb P_3 mapsto mathbb P_2 $, т.е. при таком отображении происходит понижение степени полинома, по крайней мере на $ 1_{} $. И действительно, если $ p(x)=a_0x^3+a_1x^2+a_2x+a_3 $, то
$$ x^2 p^{prime prime} (x) + p^{prime} (x) — 6 p(x) equiv
$$
$$
equiv (-4,a_1+3,a_0)x^2+(2,a_1-6,a_2)x+(a_2-6,a_3) . $$
Теперь понятно, что $ mathcal{I}m (mathcal A) subset mathbb P_2 $, а, на самом деле, это включение может быть заменено на равенство. Действительно, в соответствии с теоремой 2, имеем:
$$ mathcal{I}m (mathcal A)= {mathcal L}left(mathcal A (1),mathcal A (x),mathcal A (x^2),mathcal A (x^3) right)=
$$
$$
= {mathcal L}left(-6,,-6,x+1 ,, -4,x^2+2,x ,, 3,x^2 right) = mathbb P_2 $$
поскольку три из четырех получившихся полиномов линейно независимы.
Теперь найдем $ mathcal{K}er (mathcal A) $, или, в альтернативной формулировке, подмножество решений дифференциального уравнения
$$ x^2 p^{prime prime} (x) + p^{prime} (x) — 6 p(x)=0 $$
во множестве $ mathbb P_3 $ (полиномов степени не выше третьей). Воспользуемся уже выведенной выше формулой для образа произвольного полинома $ p(x) in mathbb P_3 $.
Этот образ будет тождественно равным нулю полиномом при выполнении условий
$$ -4,a_1+3,a_0=0, 2,a_1-6,a_2=0, a_2-6,a_3=0 . $$
Решаем эту систему:
$$ a_0=frac{4}{3} a_1, a_2=frac{1}{3} a_1, a_3=frac{1}{18} a_1 . $$
Таким образом,
$$ mathcal{K}er (mathcal A) = left{ lambda (24,x^3+18,x^2+6,x+1) mid lambda in mathbb R right} . $$
♦
Т
Теорема 4. Пусть $ {X_1,dots,X_{{mathfrak{r}}}} $ — относительный базис $ mathbb V_{} $ над $ mathcal{K}er (mathcal{A}) $. Тогда система $ {mathcal{A}(X_1),dots,mathcal {A}(X_{{mathfrak{r}}}) } $ образует базис $ mathcal{I}m (mathcal{A}) $.
Доказательство. Любой вектор $ Xin mathbb V $ представи́м в виде $ X=X_{ast}+alpha_1X_1+dots+ alpha_{{mathfrak{ r}}}X_{{mathfrak{r}}} $, где $ X_{ast} in mathcal{K}er (mathcal{A}) $. Тогда $ mathcal{A}(X) in mathcal{L} ( mathcal{A}(X_1),dots, mathcal{A}(X_{{mathfrak {r}}})) $ и, следовательно,
$$ mathcal{I}m (mathcal{A}) = mathcal L ( mathcal{A}(X_1),dots, mathcal{A}(X_{{mathfrak{r}}})) . $$
Если векторы $ mathcal{A}(X_1),dots,mathcal{A}(X_{{mathfrak{r}}}) $ удовлетворяют равенству:
$$ beta_1 mathcal{A}(X_1) boxplus dots boxplus beta_{{mathfrak{r}}} mathcal{A}(X_{{mathfrak{r}}})= mathbb O’ , $$
то $ beta_1 X_1 + dots + beta_{{mathfrak{r}}} X_{{mathfrak{r}}} in mathcal{K}er (mathcal{A}) $. На основании определения относительного базиса из такого равенства необходимо следует $ beta_1 = dots = beta_{{mathfrak{r}}}=0 $. Таким образом,
система $ {mathcal A(X_1),dots,mathcal A(X_{{mathfrak{r}}}) } $ л.н.з.
♦
Т
Теорема 5. Имеет место равенство:
$$ dim mathbb V=dim left( mathcal{K}er (mathcal A) right) + dim left( mathcal{I}m (mathcal A) right) = operatorname{dfc}(mathcal A )+ operatorname{rank}(mathcal A ) .$$
Доказательство
☞
ЗДЕСЬ.
Утверждение $ mathbb V= mathcal{K}er (mathcal A) oplus mathcal{I}m (mathcal A) $ (здесь $ oplus $ означает прямую сумму подпространств ),
вообще говоря, неверно!
Т
Теорема 6. Пусть $ mathbb V_1 $ — линейное подпространство $ mathbb V_{} $, а $ mathbb W_1 $ — линейное подпространство $ mathbb W $, причем
$$
dim mathbb V_1 + dim mathbb W_1 =dim mathbb V .
$$
Тогда существует линейное отображение
$ mathcal A : mathbb V longmapsto mathbb W $ такое, что
$$
mathcal{K}er (mathcal A ) =mathbb V_1 , quad mathcal{I}m (mathcal A )=mathbb W_1 .
$$
Определенные в настоящем пункте множества $ mathcal{K}er (mathcal A) $ и $ mathcal{I}m(mathcal A) $ позволяют полностью решить и следующую задачу:
Задача. Установить множество всех прообразов вектора $ Y ne mathbb O^{prime} $ при линейном отображении $ mathcal A_{} $ .
Т
Теорема 7. Если $ Y notin mathcal{I}m(mathcal A) $, то у вектора $ Y in mathbb W $ не существует прообраза в $ mathbb V_{} $. Если $ X_{0} in mathbb V $ — какой-то из прообразов вектора $ Y_{} $, то все множество прообразов этого вектора является линейным многообразием в $ mathbb V_{} $, а именно:
$$ X_0 + mathcal{K}er (mathcal A) . $$
Матрица линейного отображения
Рассмотрим линейное отображение $ mathcal A: mathbb V longmapsto mathbb W $,
и пусть $ {X_1,dots,X_n} $ — базис $ mathbb V_{} $, а
$ {Y_1,dots,Y_m} $ — базис $ mathbb W_{} $. Найдем координаты векторов
$ mathcal A(X_1),dots,mathcal A(X_n) $ в базисе $ {Y_1,dots,Y_m} $:
$$
left{ begin{array}{ccr}
mathcal A(X_1)&=&{color{RubineRed} alpha }_{11}Y_1 boxplus {color{RubineRed} alpha }_{21}Y_2 boxplus dots boxplus {color{RubineRed} alpha }_{m1}Y_m, \
mathcal A(X_2)&=&{color{Green} alpha }_{12}Y_1 boxplus {color{Green} alpha }_{22}Y_2 boxplus dots boxplus {color{Green} alpha }_{m2}Y_m, \
dots & & dots, \
mathcal A(X_n)&=&alpha_{1n}Y_1 boxplus alpha_{2n}Y_2 boxplus dots boxplus alpha_{mn}Y_m.
end{array} right.
$$
Матрица
$$
{mathbf A}= left(begin{array}{cccc}
{color{RubineRed} alpha } _{11} & {color{Green} alpha }_{12}& dots & alpha_{1n} \
{color{RubineRed} alpha } _{21} & {color{Green} alpha }_{22}& dots & alpha_{2n} \
vdots & & & vdots \
{color{RubineRed} alpha } _{m1} & {color{Green} alpha }_{m2}& dots & alpha_{mn}
end{array}
right)_{mtimes n},
$$
по столбцам которой стоят координаты образов базисных векторов, называется матрицей линейного отображения $ mathcal A_{} $ в выбранных базисах.
Почему запись координат в матрицу производится по столбцам? Казалось бы, естественней ставить их по строкам Объяснение этому решению будет дано ниже.
Т
Теорема 1. Координаты произвольного вектора
$ X=x_1X_1+dots+x_nX_n $ и его образа $ mathcal A (X)=y_1Y_1 boxplus dots boxplus y_mY_m $
связаны формулой:
$$
left(begin{array}{l}
y_1 \ vdots \ y_m
end{array}
right) =
{mathbf A}left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right) .
$$
Вот именно для этой последней формулы необходимо было «транспонировать» запись матрицы линейного отображения в начале настоящего пункта.
Доказательство. С помощью приведенных выше формул для $ mathcal A (X_1), dots, mathcal A (X_n) $ получаем:
$$
begin{array}{rcl}
mathcal A (X)&=&mathcal A (x_1X_1+dots+x_nX_n)=x_1mathcal A (X_1) boxplus dots boxplus
x_nmathcal A (X_n)= \
&=&x_1 (alpha_{11}Y_1 boxplus dots boxplus alpha_{m1}Y_m) boxplus dots boxplus
x_n(alpha_{1n}Y_1 boxplus dots boxplus alpha_{mn}Y_m)= \
&=&underbrace{(x_1alpha_{11} +dots+x_nalpha_{1n})}_{y_1}Y_1 boxplus dots boxplus
underbrace{(x_1alpha_{m1}+dots+x_nalpha_{mn})}_{y_m}Y_m,
end{array}
$$
откуда и следует утверждение теоремы.
♦
П
Пример. Найти матрицу линейного отображения
$$
mathcal A left(begin{array}{c}
x_1 \ x_2 \ x_3
end{array}
right)=
left(begin{array}{c}
x_3 \ 0 \x_1+x_2+x_3 \ x_1+x_2-x_3
end{array}
right)
$$
в стандартных базисах пространств
$$
overbrace{left{underbrace{left[ begin{array}{c} 1 \ 0 \ 0 end{array} right]}_{=mathfrak e_{_1}} ,
underbrace{left[ begin{array}{c} 0 \ 1 \ 0 end{array} right]}_{=mathfrak e_{_2}},
underbrace{left[ begin{array}{c} 0 \ 0 \ 1 end{array} right]}_{=mathfrak e_{_3}}
right}}^{mathbb R^3} quad u quad
overbrace{left{
underbrace{left[ begin{array}{c} 1 \ 0 \ 0 \ 0 end{array} right]}_{={mathfrak E_{_1}}} ,
underbrace{left[ begin{array}{c} 0 \ 1 \ 0 \0 end{array} right]}_{=mathfrak E_{_2}},
underbrace{left[ begin{array}{c} 0 \ 0 \ 1 \0 end{array} right]}_{=mathfrak E_{_3}} ,
underbrace{left[ begin{array}{c} 0 \ 0 \ 0 \1 end{array} right]}_{=mathfrak E_{_4}}
right}
}^{mathbb R^4}
$$
Решение.
$$ mathcal A(mathfrak e_1)=
left[ begin{array}{c} 0 \ 0 \ 1 \ 1 end{array} right]=0cdot mathfrak E_{_1}+0cdot mathfrak E_{_2}+1cdot mathfrak E_{_3}+1cdot mathfrak E_{_4} ;quad mathcal A(mathfrak e_2)=
left[ begin{array}{c} 0 \ 0 \ 1 \ 1 end{array} right]=0cdot mathfrak E_{_1}+0cdot mathfrak E_{_2}+1cdot mathfrak E_{_3}+1cdot mathfrak E_{_4} ;
$$
$$
mathcal A(mathfrak e_3)=
left[ begin{array}{r} 1 \ 0 \ 1 \ -1 end{array} right]=1cdot mathfrak E_{_1}+0cdot mathfrak E_{_2}+1cdot mathfrak E_{_3}-1cdot mathfrak E_{_4} .
$$
Матрица отображения $ mathcal A_{} $ в выбранных базисах:
$$ mathbf A=
left(begin{array}{ccr}
0 & 0 & 1 \
0 & 0 & 0 \
1& 1 & 1 \
1 & 1 & -1
end{array}
right)
$$
совпадает с матрицей коэффициентов при переменных $ x_1,x_2,x_3 $ в выражениях координат вектора $ mathcal A(X) $.
♦
П
Пример. Найти матрицу линейного отображения пространства полиномов $ mathbb P_3 $ в $ mathbb P_2 $, задаваемого формулой:
$$ mathcal A left(p(x)right) = x^2 p^{prime prime} (x) + p^{prime} (x) — 6 p(x) . $$
Базисом пространства $ mathbb P_3 $ выбран $ {1,x,x^2,x^3} $, а базис пространства
$ mathbb P_2 $ состоит из полиномов Лежандра
$$ {P_0(x)=1, P_1(x)= x, P_2(x)=frac{1}{2}(3,x^2-1) } .$$
Решение. В предыдущем ПУНКТЕ уже были получены выражения:
$$ mathcal A(1)=-6, mathcal A(x)=-6,x+1, mathcal A(x^2)=-4,x^2+2,x
, mathcal A(x^3)=3,x^2 .$$
Если бы базис пространства $ mathbb P_2 $ составляли полиномы, входящие в базис исходного пространства,
т.е. $ {1,x,x^2} $, то матрица линейного отображения построилась бы достаточно просто:
$$
mathbf B=
left(
begin{array}{rrrr}
-6 & 1 & 0 & 0 \
0 &-6 & 2 & 0 \
0 & 0 & -4 & 3 \
end{array}
right) .
$$
Однако базис пространства $ mathbb P_2 $ отличается от $ {1,x,x^2} $ в последнем полиноме: $ P_2(x) notequiv x^2 $. Координаты $ mathcal A(1) $ и $ mathcal A(x) $ остаются прежними, а вот $ mathcal A(x^2) $ и $ mathcal A(x^3) $ приходится переписывать под базис из полиномов Лежандра:
$$ -4,x^2+2,x equiv a_{13}cdot 1 + a_{23}cdot x + a_{33} cdot left( frac{1}{2}(3,x^2-1)
right) . $$
Откуда получаем: $ a_{13}=-4/3, a_{23}=2, a_{33}=-8/3 $. Аналогично
$$ 3,x^2equiv P_0(x)+2,P_2(x) $$
и, следовательно, матрица линейного отображения:
$$
mathbf A=
left(
begin{array}{rrrr}
-6 & 1 & -4/3 & 1 \
0 &-6 & 2 & 0 \
0 & 0 & -8/3 & 2 \
end{array}
right) .
$$
♦
Т
Теорема 2. Существует изоморфизм между линейным пространством $ {mathcal H}om(mathbb V,mathbb W) $ (линейных отображений из $ mathbb V_{} $ в $ mathbb W_{} $)
и линейным пространством матриц $ mathbb R^{mtimes n } $.
Фактически теоремы $ 1_{} $ и $ 2_{} $ сводят рассмотрение произвольного линейного отображения $ mathcal A_{} $ пространства $ mathbb V_{} $ в пространство $ mathbb W_{} $ к рассмотрению отображения арифметического пространства $ n_{} $-компонентных столбцов в арифметическое пространство $ m_{} $-компонентных столбцов
$$ Y=mathbf AX quad mbox{ при } quad Xin mathbb R^n, Yin mathbb R^m ; $$
это отображение задается $ mtimes n_{} $-матрицей $ mathbf A_{} $. Получается, что для полного задания исходного линейного отображения достаточно знать только результат его действия на базисные векторы пространства $ mathbb V_{} $. После фиксирования базисов обоих пространств и установления матрицы линейного отображения, можно «забыть» о природе этих пространств и исследовать свойства отображения в «переводе на язык» умножения матрицы на столбец. В частности, «почти даром» получаем следующий результат:
Т
Теорема 3. Если $ A_{} $ — матрица линейного отображения $ mathcal A_{} $ в каких-то выбранных базисах пространств $ mathbb V_{} $ и $ mathbb W_{} $, то
$$operatorname{rank} (mathcal A)=operatorname{rank}( A ), operatorname{dfc} (mathcal A)=n-operatorname{rank}( A ) .$$
Ядро линейного отображения
$$ Y=AX quad mbox{ при } quad Xin mathbb R^n, Yin mathbb R^m, quad A in mathbb R^{mtimes n } $$
часто называется ядром матрицы $ A_{} $ или нуль-пространством матрицы $ A_{} $ и также обозначается $ {mathcal K}er (A) $. Наряду с определением ядра матрицы через свойства отображения
$ AX $, можно дать ему и другую интерпретацию:
Т
Теорема 4. Если в пространстве $ mathbb R_{}^{n} $, рассматриваемом как пространство $ n_{} $-строк, ввести скалярное произведение формулой
$$ langle X,Y rangle=x_1y_1+x_2y_2+dots+x_ny_n quad npu quad X=[x_1,x_2,dots,x_n], Y=[y_1,y_2,dots,y_n] , $$
то $ {mathcal K}er (A) $ образует ортогональное дополнение линейной оболочки строк этой матрицы в пространстве $ mathbb R_{}^{n} $:
$$ {mathcal K}er (A) bot mathcal L ( A^{[1]}, A^{[2]},dots, A^{[m]} ),
{mathcal K}er (A) oplus mathcal L ( A^{[1]}, A^{[2]},dots, A^{[m]} ) = mathbb R_{}^{n} .
$$
Дефектом матрицы4) $ A_{} $ будем называть размерность ядра этой матрицы, или, что то же, число элементов фундаментальной системы решений системы линейных однородных уравнений $ AX=mathbb O $. В соответствии с результатами, приведенными
☞
ЗДЕСЬ:
$$ operatorname{dfc}(A) = n — mathfrak r npu mathfrak r = operatorname{rank}(A) . $$
Вернемся теперь к общему случаю линейного пространства.
Задача. Как изменяется матрица линейного отображения $ mathcal A_{} $ при изменении
базисов?
Т
Теорема 5. Пусть $ {{mathfrak X}_1,dots,{mathfrak X}_n } $ — новый базис пространства $ mathbb V_{} $, $ { {mathfrak Y}_1,dots,{mathfrak Y}_m } $— новый базис $ mathbb W_{} $, и в этих
базисах линейное отображение $ mathcal A $ имеет матрицу $ {mathbf B} $. Если $ C_{} $ — матрица перехода от старого базиса к новому в пространстве $ mathbb V_{} $, а $ D_{} $ — матрица перехода от старого базиса к новому в пространстве $ mathbb W_{} $, то
$$ {mathbf B}=D^{-1}cdot {mathbf A} cdot C . $$

Доказательство. Действительно, координаты произвольного вектора
$$ X=x_1X_1+dots+x_nX_n = {mathfrak x}_1 {mathfrak X}_1+dots+ {mathfrak x}_n {mathfrak X}_n ,$$
и его образа
$$ Y =mathcal A(X)=y_1Y_1 boxplus dots boxplus y_mY_m= {mathfrak y}_1{mathfrak Y}_1 boxplus dots boxplus {mathfrak y}_m{mathfrak Y}_m $$
связаны следующими соотношениями: с одной стороны, на основании теоремы 1,
$$
left(begin{array}{c}
y_1 \ vdots \ y_m
end{array}
right) = {mathbf A}left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right), qquad
left(begin{array}{c}
{mathfrak y}_1 \ vdots \ {mathfrak y}_m
end{array}
right) = {mathbf B}left(begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array}
right) .
$$
с другой стороны, на основании результатов пункта
☞
ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ЗАМЕНЕ БАЗИСА,
$$
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)=C left(begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array}
right),
qquad
left(begin{array}{c}
y_1 \ vdots \ y_m
end{array}
right)=D left(begin{array}{c}
{mathfrak y}_1 \ vdots \ {mathfrak y}_m
end{array}
right).
$$
Получаем цепочку равенств:
$$
{mathbf B}left(begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array}
right)=
left(begin{array}{c}
{mathfrak y}_1 \ vdots \ {mathfrak y}_m
end{array}
right) =D^{-1}left(begin{array}{c}
y_1 \ vdots \ y_m
end{array}
right)=D^{-1} {mathbf A}left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)=D^{-1} {mathbf A} C left(begin{array}{c}
{mathfrak x}_1 \ {mathfrak x}_2 \ vdots \ {mathfrak x}_n
end{array}
right).
$$
Поскольку равенство справедливо для любого столбца координат, то оно справедливо и для столбцов
$$
left(begin{array}{c}
1 \ 0 \ vdots \ 0
end{array}
right) ,
left(begin{array}{c}
0 \ 1 \ vdots \ 0
end{array}
right)
,dots,
left(begin{array}{c}
0 \ 0 \ vdots \ 1
end{array}
right) .
$$
Объединяя полученные $ n_{} $ равенств в одно матричное, получаем $ {mathbf B}E = D^{-1} {mathbf A} C E $, где $ E_{} $ — единичная матрица порядка $ n_{} $. Отсюда и следует утверждение теоремы.
♦
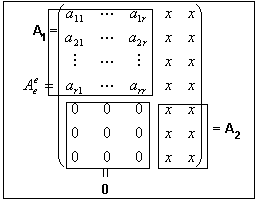
Канонический вид матрицы линейного отображения
Задача. Подобрать базисы пространств $ mathbb V_{} $ и $ mathbb W_{} $ так, чтобы матрица заданного линейного отображения $ mathcal A $ имела наиболее простой вид.
Найдем относительный базис $ mathbb V_{} $ над $ mathcal{K}er (mathcal A) $, т.е. базис $ mathcal{K}er (mathcal A) $ дополним до базиса $ mathbb V_{} $:
$$
{X_1,dots,X_{{mathfrak r}}} gets mbox{ относительный базис }
mathbb V mbox{ над } mathcal{K}er (mathcal A)
$$
$$
{X_{{mathfrak r}+1},dots,X_{n} } gets mbox{ базис } mathcal{K}er (mathcal A)
$$
Было доказано (см.
☞
теорему 4 ), что $ {mathcal A(X_1),dots,mathcal A(X_{{mathfrak r}}) } subset mathbb W $ является базисом $ mathcal{I}m (mathcal A) $. Составим базис $ mathbb W_{} $ ее дополнением:
$$
{mathcal A(X_1),dots,mathcal A(X_{{mathfrak r}})} gets
mbox{ базис } mathcal{I}m (mathcal A)
$$
$$
{ Y_{{mathfrak r}+1},dots,Y_{m}} gets mbox{ относительный базис }
mathbb W mbox{ над } mathcal{I}m (mathcal A)
$$
Т
Теорема. В выбранных базисах матрица линейного отображения $ mathcal A $ имеет следующий канонический вид:
$$
{mathbf B}=left( begin{array}{cccccc}
1 & & & & \
&1 & & &mathbb O\
& &ddots& & \
& & & 1 & \
& & & & \
&mathbb O & & & mathbb O
end{array}
right)
begin{array}{r}
left. begin{array}{r}
\ \ \ \ end{array} right} \
\ \
end{array}
begin{array}{r}
\ \ {mathfrak r} \ \ \
\ \
end{array}
= left( begin{array}{ll}
E_{{mathfrak r}times {mathfrak r}} & mathbb O_{{mathfrak r}times (n-{mathfrak r})} \
mathbb O_{(m-{mathfrak r})times {mathfrak r}} & mathbb O_{(m-{mathfrak r})times (n-{mathfrak r})}
end{array}
right) .
$$
Здесь $ {mathfrak r}= operatorname{rank} (mathcal A) $.
Доказательство. Разложим образы базисных векторов $ {X_1,dots,X_n} $ по базису пространства $ mathbb W $:
$$
begin{array}{llllllll}
mathcal A(X_1) & = 1cdot mathcal A(X_1) & boxplus 0 cdot mathcal A(X_2) & boxplus dots & boxplus 0cdot mathcal A(X_{mathfrak r})&
boxplus 0cdot Y_{{mathfrak r}+1}&boxplusdots &boxplus 0cdot Y_m, \
mathcal A(X_2) & = 0cdot mathcal A(X_1) & boxplus 1 cdot mathcal A(X_2) & boxplus dots & boxplus 0cdot mathcal A(X_{mathfrak r})&
boxplus 0cdot Y_{{mathfrak r}+1}&boxplus dots & boxplus 0cdot Y_m, \
dots & & & dots \
mathcal A(X_{mathfrak r}) & = 0cdot mathcal A(X_1) & boxplus 0 cdot mathcal A(X_2) & boxplus dots & boxplus 1cdot mathcal A(X_{mathfrak r})&
boxplus 0cdot Y_{{mathfrak r}+1}&boxplus dots & boxplus 0cdot Y_m,
end{array}
$$
а $ mathcal A(X_{{mathfrak r}+1})=mathbb O^{prime},dots, mathcal A(X_{m})=mathbb O^{prime} $ по определению
$ mathcal{K}er (mathcal A) $.
♦
Матричный формализм
§
Настоящий пункт может быть пропущен при первоначальном чтении.
В частном случае отображения $ mathbb R^{n} $ в $ mathbb R^{m} $, задаваемого матрицей в стандартных базисах пространств, результат последнего пункта можно переформулировать в следующем виде.
Т
Теорема. Любую матрицу $ A_{mtimes n} $ ранга $ mathfrak r > 0 $ можно представить в виде произведения
$$ A=Dcdot A_d cdot tilde C $$
при
$$
A_d =left( begin{array}{cccccc}
1 & & & & \
&1 & & &mathbb O\
& &ddots& & \
& & & 1 & \
& & & & \
&mathbb O & & & mathbb O
end{array}
right)
begin{array}{r}
left. begin{array}{r}
\ \ \ \ end{array} right} \
\ \
end{array}
begin{array}{r}
\ \ {mathfrak r} \ \ \
\ \
end{array}
= left( begin{array}{ll}
E_{{mathfrak r}times {mathfrak r}} & mathbb O_{{mathfrak r}times (n-{mathfrak r})} \
mathbb O_{(m-{mathfrak r})times {mathfrak r}} & mathbb O_{(m-{mathfrak r})times (n-{mathfrak r})}
end{array}
right) $$
и при невырожденных матрицах $ D_{mtimes m} $ и $ tilde C_{ntimes n} $.
Здесь матрица $ tilde C $ соответствует матрице $ C^{-1} $ из теоремы предыдущего пункта.
П
Пример. Представить матрицу
$$ A =
left(
begin{array}{rrr}
2 & — 1 & 0 \
-2/3 & 5/3 & 4/3 \
2 & — 1 & 0 \
-2/3 & 5/3 & 4/3
end{array}
right)
$$
в виде произведения из теоремы.
Решение. Здесь $ operatorname{rank} (A) =2 $, так что
$$
A_d=
left(begin{array}{ccc}
1 & 0 & 0 \
0 & 1 & 0 \
0 & 0 & 0 \
0 & 0 & 0
end{array}
right) , .
$$
Для нахождения матрицы $ C $ из теоремы предыдущего пункта ищем базис ядра отображения $ AX $, т.е. попросту говоря, фундаментальную систему решений системы уравнений $ AX=mathbb O $. Можно взять $ X=[1,2,-2]^{top} $. Этот столбец будет третьим столбцом матрицы $ C $. Первые два — любые линейно независимые с этим столбцом. Например
$$
C=
left(begin{array}{ccr}
1 & 0 & 1 \
0 & 1 & 2 \
0 & 0 & -2
end{array}
right) , .
$$
Теперь умножаем столбцы $ C_{[1]} $ и $ C_{[2]} $ на матрицу $ A $ (слева). Полученные столбцы
$$
D_{[1]}=left[2,-2/3,2,-2/3right]^{top}, D_{[2]}=left[-1,5/3,-1,5/3right]^{top}
$$
будут первыми столбцами искомой матрицы $ D $. Оставшиеся два выбираем произвольными линейно независимыми с уже найденными.
$$
D=
left(
begin{array}{rrrr}
2 & — 1 & 1 & 0 \
-2/3 & 5/3 & 0 & 1 \
2 & -1 & 0 & 0 \
-2/3 & 5/3 & 0 & 0
end{array}
right), quad tilde C= C^{-1} =
left(
begin{array}{rrr}
— 1 & 0 & 1/2 \
0 & 1 & 1 \
0 & 0 & -1/2
end{array}
right) , .
$$
♦
Разложение матрицы в произведение из теоремы не единственно. Так, например, матрицу $ tilde C $ можно выбрать в классе ортогональных матриц. Из этого замечания можно «перебросить мостик» к похожему разложению матрицы в произведение, известному как сингулярное разложение. Очень полезно в задачах обработки данных.
Линейный оператор
Линейное отображение векторного пространства $ mathbb V_{} $
в себя
$$ mathcal A : mathbb V longmapsto mathbb V $$
называется линейным преобразованием $ mathbb V_{} $ или линейным оператором на $ mathbb V_{} $. Подробнее
☞
ЗДЕСЬ.
Аффинное отображение
Линейные отображения пространства $ mathbb V_{} $ в пространство $ mathbb W_{} $ составляют подмножество более широкого класса отображений.
Рассмотрим пример $ 5_{} $
☞
ЗДЕСЬ. Отображение пространства $ mathbb R^{n}_{} $ в пространство $ mathbb R^{m} $, задаваемое соотношением
$$
begin{array}{ll}
tilde{mathcal A}
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)
&= left(begin{array}{c}
a_{11}x_1+a_{12}x_2 + cdots + a_{1n}x_n +b_1 \
dots \
a_{m1}x_1+a_{m2}x_2 + cdots + a_{mn}x_n + b_m
end{array}
right)= \
&=left(begin{array}{cccc}
a_{11} & a_{12}& dots & a_{1n} \
dots & & & dots \
a_{m1} & a_{m2}& dots & a_{mn}
end{array}
right) cdot
left(begin{array}{c}
x_1 \ x_2 \ vdots \ x_n
end{array}
right)+
left(begin{array}{c}
b_1 \ vdots \ b_m
end{array}
right)
end{array}
$$
будет линейным отображением при условии, что $ b_1=0,dots, b_m=0 $ и не будет линейным отображением при хотя бы одном из чисел $ b_1,dots,b_{m} $ отличном от нуля.
Тем не менее, по своему внешнему виду отображение из $ mathbb R^{n}_{} $ в $ mathbb R^{m} $, задаваемое в матричном виде как $ A, X + mathcal B $ напоминает линейную функцию $ a, x+b $, действующую в $ mathbb R $. Кажется очень несправедливым лишать подобные отображения эпитета линейный, однако же именно это и произошло в линейной алгебре и геометрии.
Аффинным5) отображением линейного векторного пространства $ mathbb V_{} $ с операцией сложения векторов, обозначаемой $ +_{} $,
в линейное векторное пространство $ mathbb W_{} $ с операцией сложения векторов, обозначаемой $ boxplus_{} $,
называется функция вида
$$ mathcal A(X) boxplus_{} mathcal B npu X in mathbb V . $$
Здесь $ mathcal A $ — линейное отображение $ mathbb V_{} $ в $ mathbb W_{} $, а $ mathcal B $ — некоторый вектор пространства $ mathbb W_{} $.
Образно говоря, аффинное отображение может быть получено сдвигом некоторого линейного отображения. Фактически же определение содержит в себе объяснение той причины, по которой аффинные отображения изучаются менее подробно, чем линейные: первые сводятся ко вторым.
Основное геометрическое свойство аффинного отображения проявилось в
☞
ПУНКТЕ для отображения линейного.
Т
Теорема. Аффинное отображение отображает произвольное линейное многообразие пространства $ mathbb V_{} $ в линейное же многообразие пространства $ mathbb W_{} $. Аффинное отображение отображает параллельные многообразия пространства $ mathbb V_{} $ в параллельные же многообразия пространства $ mathbb W_{} $.
=>
Аффинное отображение отображает произвольную прямую пространства $ mathbb V_{} $ в прямую или точку пространства $ mathbb W $.
Почему рассматриваются только линейные отображения?
Почему во всех вузовских курсах алгебры не рассматриваются более сложные отображения, задаваемые, например, нелинейными полиномами:
$$
left(
begin{array}{l}
x_1 \
x_2 \
x_3
end{array}
right) mapsto
left(
begin{array}{c}
x_1^4-sqrt{2} x_1^2x_3 + 17, x_2^5+2, x_1 — 3,x_3-14 \
x_2^{18}- x_2^7+x_1x_2^4x_3^6-x_1-5,x_2+2 \
x_2x_3^3+x_3-6 \
x_1-2,x_2+6,x_3-33
end{array}
right) ?
$$
— Да потому что про них мало что понятно. Попытки обобщения на нелинейный случай практически любого понятия, введенного для линейного отображения, приводят к нерешенной задаче. Так, для обобщения понятия ядра придется решить не решенную на настоящий момент 16-ю проблему Гильберта;
еще одна нерешенная проблема — проблема якобиана — связана с существованием обратного к полиномиальному отображению.
В одном частном случае нелинейные отображения сравнительно хорошо изучены — это отображения $ mathbb R^2 mapsto mathbb R^2 $, заданные условиями:
$$
left(
begin{array}{l}
x \
y
end{array}
right) mapsto
left(
begin{array}{l}
u(x,y) \
v(x,y)
end{array}
right) quad npu quad frac{partial u}{partial x}=frac{partial v}{partial y}, frac{partial u}{partial y}=-frac{partial v}{partial x} ;
$$
(функции $ u_{} $ и $ v_{} $ — не обязательно полиномы).
Последние два условия называются условиями Коши-Римана (Даламбера-Эйлера); из них следует, что каждая из функций $ u_{} $ и $ v_{} $ является гармонической функцией, т.е. удовлетворяет тождествам:
$$
frac{partial^2 u}{partial x^2}+frac{partial^2 u}{partial y^2}equiv 0,quad frac{partial^2 v}{partial x^2}+frac{partial^2 v}{partial y^2} equiv 0 .
$$
Подобные отображения рассматриваются в разделе математики, известном как КОМПЛЕКСНЫЙ АНАЛИЗ или теория функций комплексной переменной (ТФКП).
Как же исследовать нелинейные отображения в общем случае? — Ну, по крайней мере, можно попытаться свести их исследование к линейному случаю. Рассмотрим пример отображения из начала
пункта
$$
left(
begin{array}{l}
x_1 \
x_2 \
x_3
end{array}
right) mapsto
left(
begin{array}{c}
x_1^4-sqrt{2} x_1^2x_3 + 17, x_2^5+2, x_1 — 3,x_3-14 \
x_2^{18}- x_2^7+x_1x_2^4x_3^6-x_1-5,x_2+2 \
x_2x_3^3+x_3-6 \
x_1-2,x_2+6,x_3-33
end{array}
right) =
$$
$$
=left(
begin{array}{r}
-14 \
2 \
-6 \
-33
end{array}
right)
+
left(
begin{array}{c}
2, x_1 — 3,x_3 \
-x_1-5,x_2 \
x_3 \
x_1-2,x_2+6,x_3
end{array}
right)
+ dots
$$
В разложении каждого элемента вектора отбросим все члены степени выше первой. В результате мы получили отображение, которое можно представить в матричном виде
$$
left(
begin{array}{l}
x_1 \
x_2 \
x_3
end{array}
right) mapsto
underbrace{left(
begin{array}{r}
-14 \
2 \
-6 \
-33
end{array}
right)}_{=mathcal B}+
underbrace{left(
begin{array}{rrr}
2 & 0 & — 3 \
-1 & -5 & 0 \
0 & 0 & 1 \
1 & -2 & 6
end{array}
right)}_{=A}
left(
begin{array}{l}
x_1 \
x_2 \
x_3
end{array}
right) .
$$
Это новое отображение является аффинным отображением пространства $ mathbb R^{3} $ в пространство $ mathbb R^{4} $. Таким образом, исходное, существенно нелинейное, отображение $ mathcal F(X) $ фактически заменили аффинным $ tilde{mathcal A}(X)=AX+mathcal B $. Насколько такая замена оправдана? — Ну, по крайней мере, в одной точке эти отображения совпадают: $ mathcal F(mathbb O) = tilde {mathcal A}(mathbb O) $. Трудно ожидать, что они будут совпадать еще где-нибудь. Однако же, в малой окрестности точки $ mathbb O $ значения этих двух функций оказываются близкими!
$$
begin{array}{lll}
mathcal F left(
begin{array}{r}
0.01 \
-0.02\
0.07
end{array}
right)=
left(
begin{array}{r}
-14.19000994 \
2.090000000 \
-5.930006860 \
-32.53000000
end{array}
right); &
mathcal F left(
begin{array}{r}
0.05 \
0.12\
-0.14
end{array}
right)=
left(
begin{array}{r}
-13.47907577 \
1.349999642 \
-6.140329280 \
-34.03000000
end{array}
right); & mathcal F left(
begin{array}{r}
-0.30 \
0.25\
-0.24
end{array}
right)=
left(
begin{array}{r}
-13.82475143 \
1.049938741 \
-6.243456000 \
-35.24000000
end{array}
right) ; dots
\
tilde{mathcal A}
left(
begin{array}{r}
0.01 \
-0.02\
0.07
end{array}
right)=
left(
begin{array}{r}
-14.19000000 \
2.090000000 \
-5.930000000 \
-32.53000000
end{array}
right) ; &
tilde{mathcal A}
left(
begin{array}{r}
0.05 \
0.12\
-0.14
end{array}
right)=
left(
begin{array}{r}
-13.48000000 \
1.350000000\
-6.140000000 \
-34.03000000
end{array}
right) &
tilde{mathcal A} left(
begin{array}{r}
-0.30 \
0.25\
-0.24
end{array}
right)=
left(
begin{array}{r}
-13.88000000 \ 1.050000000 \ -6.240000000 \ -35.24000000
end{array}
right); dots
end{array}
$$
Иными словами, в некоторой достаточно малой окрестности6) точки $ X_0=mathbb O_{} $ нелинейное отображение аппроксимируется аффинным. А чем аппроксимировать за пределами этой окрестности, скажем, в окрестности вектора $ X_0=[1,-1,1]^top $? — Для этого придется привлекать аппарат разложения нелинейных функций нескольких переменных в ряды Тейлора. К счастью, функции нашего примера являются полиномиальными, поэтому этот ряд не будет содержать бесконечного числа членов. Воспользовавшись материалом пункта
☞
ФОРМУЛА ТЕЙЛОРА, получим:
$$
mathcal F left(
begin{array}{r}
x_1 \
x_2\
x_3
end{array}
right)
=
left(
begin{array}{c}
-31-sqrt{2} \
9 \
-6 \
-24
end{array}
right)+
left(
begin{array}{rrr}
(6-2,sqrt{2})(x_1-1) &+ 85, (x_2+1) & +(-sqrt{2}-3)(x_3-1)\
&-34,(x_2+1) & +6,(x_3-1) \
&(x_2+1) & -2,(x_3-1)\
(x_1-1) &- 2,(x_2+1) & +6,(x_3-1)
end{array}
right)+ dots
$$
Перепишем второе слагаемое в матричном виде:
$$
=
left(
begin{array}{c}
-31-sqrt{2} \
9 \
-6 \
-24
end{array}
right)+
left(
begin{array}{ccc}
6-2,sqrt{2} &85& -sqrt{2}-3\
0 &-34 & 6 \
0&1& -2\
1 &- 2 & 6
end{array}
right)left(
begin{array}{c}
x_1-1 \
x_2+1 \
x_3-1
end{array}
right) + dots
$$
В общем же случае, если
$$
mathcal{F} left(
begin{array}{l}
x_1 \
x_2\
vdots \
x_n
end{array}
right)=
left(
begin{array}{c}
f_1(x_1,dots,x_n) \
vdots \
f_m(x_1,dots,x_n)
end{array}
right),
$$
то, в окрестности вектора $ X_0= (x_{01},x_{02},dots,x_{0n})^{top} $ его можно аппроксимировать аффинным отображением
$$
tilde{mathcal A} left(
begin{array}{l}
y_1 \
y_2\
vdots \
y_n
end{array}
right)=
underbrace{left(
begin{array}{c}
f_1(x_{01},dots,x_{0n}) \
vdots \
f_m(x_{01},dots,x_{0n})
end{array}
right)}_{=mathcal F(X_0)}+
underbrace{left(
begin{array}{cccc}
{partial f_1}/{partial x_1} & {partial f_1}/{partial x_2} & dots & {partial f_1}/{partial x_n} \
{partial f_2}/{partial x_1} & {partial f_2}/{partial x_2} & dots & {partial f_2}/{partial x_n} \
dots & && dots \
{partial f_m}/{partial x_1} & {partial f_m}/{partial x_2} & dots & {partial f_m}/{partial x_n}
end{array}
right)}_{mathbf J}left(
begin{array}{l}
y_1 \
y_2\
vdots \
y_n
end{array}
right) ,
$$
которое рассматривается в окрестности $ Y_0=mathbb O_{} $. Здесь все частные производные в матрице $ mathbf J $ вычисляются в точке $ X_{0} $. Матрица
$$
mathbf J = left[ frac{partial f_j}{partial x_k} right]_{j=1,dots,m, atop k=1,dots,n}
$$
называется матрицей Якоби системы из $ m_{} $ функций $ {f_1(x_1,dots,x_n),dots,f_m(x_{1},dots,x_n)} $ по переменным $ x_1,dots,x_{n} $. Линейное отображение
$$
mathbf J left(
begin{array}{l}
y_1 \
y_2\
vdots \
y_n
end{array}
right)
$$
известно как дифференциал (первого порядка) функции $ mathcal F(X) $ в точке $ X_0 $.
Подводя итог, можно сказать, что линейные (аффинные) отображения служат основой анализа отображений нелинейных — но этот анализ носит локальный характер: линеаризация адекватно приближает исходное нелинейное отображение лишь в малых областях значений аргументов.