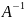Как найти матрицу обратного оператора - Исправление недочетов и поиск решений вместе с Examum.ru

0 / 0 / 0

Регистрация: 16.12.2012

Сообщений: 26

Найти матрицы оператора, обратного оператору

08.01.2015, 15:29. Показов 5873. Ответов 2

Помогите решить задачки по алгебре. Ну или хотя бы алгоритм решения напишите. А то в корне не могу понять как их решать
2. Найти матрицы оператора, обратного оператору A:R² —> R², Ax=(x¹+2x², x¹+3x²).

Programming

Эксперт

94731 / 64177 / 26122

Регистрация: 12.04.2006

Сообщений: 116,782

08.01.2015, 15:29

Ответы с готовыми решениями:

Найти матрицы и явный вид оператора
Пусть (вектор)x=(x1, x2, x3)Т, f(x)=(2×1, x2+5×3, -x1), g(x)=(x1-x2, x3+x2, 0). Найти матрицы…

Найти матрицу оператора сопряжённого для данного линейного оператора
Здравствуйте! Подскажите мне, пожалуйста, как делать данную задачу:

Матрица линейного оператора…

Как выделить символы строк от оператора к оператору ?
Работаю над тестом для кода калькулятора. Хочу сделать не простой калькулятор, а чтобы вписаное…

Операторы эквивалентные оператору присваиванияусловному оператору?
Здравствуйте уважаемые форумчане) Есть два задания, в которых я не могу понять даже смысла, будьте…

3944 / 2858 / 665

Регистрация: 08.06.2007

Сообщений: 9,668

Записей в блоге: 4

08.01.2015, 18:48

Сообщение было отмечено Staselletti как решение

Решение

Обратную матрицу ищите.

Модератор

35578 / 19476 / 4073

Регистрация: 12.02.2012

Сообщений: 32,511

Записей в блоге: 13

09.01.2015, 18:51

Выпишем матрицу этого линейного оператора:

$https://www.cyberforum.ru/cgi-bin/latex.cgi?begin{pmatrix}1 & 2\ 1 & 3end{pmatrix}$

Ее определитель равен 1*3-1*2=1, что облегчает прямое нахождение обратной матрицы. Она равна:

$https://www.cyberforum.ru/cgi-bin/latex.cgi?begin{pmatrix}3 & -2\ -1 & 1end{pmatrix}$

В том, что матрица действительно обратная исходной, можно убедиться прямым умножением:

$https://www.cyberforum.ru/cgi-bin/latex.cgi?begin{pmatrix}3 & -2\ -1 & 1end{pmatrix}*begin{pmatrix}1 & 2\ 1 & 3end{pmatrix}=begin{pmatrix}(3*1-2*1) & (3*2-2*3) \ (-1*1+1*1) & (-1*2+1*3) end{pmatrix}=begin{pmatrix}1 & 0\ 0 & 1end{pmatrix}$

Источник

Линейные операторы.[править]

Оператор называется линейным, если:

${displaystyle Theta :forall {vec {x}}:Theta {vec {x}}={vec {0}}_{y}}$ — нулевой оператор.

-тождественный оператор.

${displaystyle (A_{1}+A_{2}){vec {x}}{overset {def}{=}}A_{1}{vec {x}}+A_{2}{vec {x}}}$ — сумма двух операторов.

${displaystyle A^{2}{vec {x}}{overset {def}{=}}A(A({vec {x}}));A^{k}{vec {x}}=A(A^{k-1}({vec {x}}))}$ — степень оператора.

— умножение операторов.

Матрица линейного оператора.[править]

Возьмём базис ${displaystyle {vec {e}}_{1},dots ,{vec {e}}_{m}}$ в X,, ${displaystyle {vec {f}}_{1},dots ,{vec {f}}_{n}}$ базис в Y.

Покажем, что если известны результаты действия оператора А на базис, то оператор А полностью определён:

${displaystyle A({vec {e}}_{i})={vec {h}}_{i}in Y,i=1dots m.}$

${displaystyle forall {vec {x}}in X:{vec {x}}=sum limits _{j=1}^{m}x_{j}{vec {e}}_{j}Rightarrow A({vec {x}})=A(sum limits _{j=1}^{m}x_{j}{vec {e}}_{j})=sum limits _{j=1}^{m}x_{j}A({vec {e}}_{j})=sum limits _{j=1}^{m}x_{j}{vec {h}}_{j}.}$

Матрица оператора ${displaystyle A_{ef}=||a_{ij}||_{ntimes m}=left({begin{smallmatrix}a_{11}&a_{12}&dots &a_{1m}\dots &dots &dots &dots \a_{n1}&a_{n2}&dots &a_{nm}end{smallmatrix}}right)}$

${displaystyle A{vec {e}}_{1}=a_{11}{vec {f}}_{1}+dots +a_{n1}{vec {f}}_{n}}$

${displaystyle A{vec {e}}_{m}=a_{1m}{vec {f}}_{1}+dots +a_{nm}{vec {f}}_{n}}$

Утверждение. Если матрица ${displaystyle B=||b_{ij}||_{mtimes n}}$ осуществляет действие оператора А, то В является матрицей оператора А.

Доказательство. в базисе ${displaystyle {vec {e}}_{1},dots ,{vec {e}}_{n}{text{вектору}}{vec {e}}_{1}{text{соответствует}}left({begin{smallmatrix}1\0\vdots \0end{smallmatrix}}right)Rightarrow Bleft({begin{smallmatrix}1\0\vdots \0end{smallmatrix}}right)=left({begin{smallmatrix}a_{11}\a_{21}\vdots \a_{m1}end{smallmatrix}}right)}$

${displaystyle left({begin{smallmatrix}b_{11}&b_{12}&dots &b_{1m}\dots &dots &dots &dots \b_{n1}&b_{n2}&dots &b_{nm}end{smallmatrix}}right)left({begin{smallmatrix}1\0\vdots \0end{smallmatrix}}right)=left({begin{smallmatrix}b_{11}\b_{21}\vdots \b_{m1}end{smallmatrix}}right)=left({begin{smallmatrix}a_{11}\a_{21}\vdots \a_{m1}end{smallmatrix}}right)Rightarrow }$ первый столбец В совпадает с первым столбцом ${displaystyle A_{ef}}$ , аналогично все остальные тоже совпадают ${displaystyle Rightarrow B=A_{ef}}$

Утверждение. Если оператор \ , то ${displaystyle C_{ef}=A_{ef}+B_{ef}}$ (матрица оператора С равна сумме матриц оператора А и В)

Доказательство. ${displaystyle left(A_{ef}+B_{ef}right)left({begin{smallmatrix}x_{1}\vdots \x_{n}end{smallmatrix}}right)=A_{ef}left({begin{smallmatrix}x_{1}\vdots \x_{n}end{smallmatrix}}right)+B_{ef}left({begin{smallmatrix}x_{1}\vdots \x_{n}end{smallmatrix}}right)=A({vec {x}})+B({vec {x}})=(A+B)({vec {x}})=C({vec {x}})=C_{ef}left({begin{smallmatrix}x_{1}\vdots \x_{n}end{smallmatrix}}right)}$

Обратный оператор[править]

Если А — изоморфизм, то: возникает некоторое отображение ${displaystyle A^{-1}:A^{-1}({vec {y}})={vec {x}}.}$

Покажем, что ${displaystyle A^{-1}}$ линейный оператор:

1) ${displaystyle A^{-1}({vec {y}})rightarrow {vec {x}};A^{-1}({vec {y}}_{1})rightarrow {vec {x}}_{1}}$

${displaystyle A^{-1}({vec {y}}+{vec {y}}_{1})={vec {x}}+{vec {x}}_{1}=A^{-1}({vec {y}})+A^{-1}({vec {y}}_{1}),({text{т.к.}}A({vec {x}}+{vec {x}}_{1})=A({vec {x}})+A({vec {x}}_{1})={vec {y}}+{vec {y}}_{1}).}$

2) ${displaystyle A^{-1}(lambda {vec {y}})=lambda {vec {x}}=lambda A^{-1}({vec {y}}),({text{т.к.}}A(lambda {vec {x}})=lambda A({vec {x}})=lambda {vec {y}}).}$

Условие обратимости: — оператор обратим оператор А осуществляет изоморфизм.

Матрица обратного оператора

осуществляет изоморфизм (Ограниченный линейный оператор между нормированными пространствами называется изоморфизмом, если существует положительное вещественное число такое, что для всех векторов ) тогда ${displaystyle exists A^{-1}:Mrightarrow L}$ .

Возьмём ${displaystyle {vec {e}}_{1},dots ,{vec {e}}_{n}}$ — базис в L, ${displaystyle {vec {f}}_{1},dots ,{vec {f}}_{n}}$ — базис в M, тогда:

${displaystyle forall {vec {x}}={begin{pmatrix}x_{1}\vdots \x_{n}end{pmatrix}}=sum _{i=1}^{n}x_{i}{vec {e}}_{i};forall {vec {y}}=A({vec {x}})={begin{pmatrix}y_{1}\vdots \y_{n}end{pmatrix}}=sum _{i=1}^{n}y_{i}{vec {f}}_{i}}$

${displaystyle Y=A_{ef}XLeftrightarrow A_{ef}^{-1}Y=A_{ef}^{-1}A_{ef}XLeftrightarrow A_{ef}^{-1}Y=XRightarrow }$ матрица ${displaystyle A_{ef}^{-1}}$ осуществляет действие оператора ${displaystyle A^{-1}Rightarrow A_{ef}^{-1}}$ — матрица обратного оператора.

Источник

Единичный
(тождественный) оператор I
действует
по правилу I(x)
= x ∀x
∈
V.

Л.О.(Лин.Оператор)
f⁻¹
называется обратным по отношению к
Л.О. f,
если

=f*

=I
(или можно
Е).

Теорема: для
существования обратного оператора f
необходимо и достаточно, чтобы f
был взаимооднозначен.

Теорема: если А —
матрица линейного оператора в некотором
базисе, то

— матрица обратного оперетора в том же
базисе.

14.Собственные векторы л.О., собств. Значения, характерист. Уравнение.

Пусть f:V_n->V_n.

Опр.
Ненулевой вектор х
Vn
наз-ся
собственным
вектором
оператора f,
если fx=λx(1),
где λ–некоторое
число (λ
P),
то λ
наз-ся собственным значением.

Св-ва:1)Всякому
собств. вектору отвечает одно собств.
значение.

2)Собств.
векторы, отвечающие собственным значениям
— лин. независимы.

3)Мн-во всех
собств. векторов, отвечающих одному
собств. значению, дополненное нулевым
вектором, образует лин-ые подпространства
пространства Z_n.
Если в
некотором базисе оператор f
имеет матрицу А и
в том же базисе вектор x имеет
коорд. столбец X,
то AX= λX
или (A—
λE)X=0.
Можно записать
в матричной форме:
AX— λX,
где X—
матрица-столбец из коорд. вектора x.

Характ-им
многочленом
оператора f:V_n->V_n
называется характеристический
многочлен (x_f(λ)=det(λE—A_f))
его матрицы
в некотором базисе. Характ-кий мн-н лин.
оператора f не
зависит от выбора базиса, в котором
представлена его матрица. Уравнение
X_f(λ)=0 называется характ-ким
уравнением оператора f.
Хар. ур-ние: (-1)ⁿλⁿ+a_n_-1λⁿ^-1+…+a₁λ+
a₀=0
—
Многочлен
в левой части уравнения называется
характ-ким
мн-м. Характ.
многочлен явл-ся многочленом
n—ой
степени. Теорема.
Подобные
матрицы имеют один и тот же характ.
многочлен.

15.Правило нахождения собств. Векторов и собств. Значений

Выберем некоторый
базис e₁,e₂,e₃,…,e_n
(1), тогда в этом базисе оператор f
будет иметь некоторую матрицу А,
и Х–координатный
столбец вектора. Тот факт, что х–собств.
значения, а

–собств.
вектор оператора f,
то АХ= λХ;
(А– λE)X=0
(2). Система (2)–система линейных однородных
уравнений. Det(A–
λE)=0
(3). Решив ур-ние (3), получим характерист.
числа матрицы А.
Для нахождения собств. векторов, решим
систему: (A—
λE)X=0
.

16 Модель бездефецитной торговли

Пусть n
стран торгуют
между собой. Обозначим через

нац-ный
доход i-той
страны;

– это часть нац. дохода, которую j-тая
страна тратит на закупку товаров из
i-той
страны.

+ … +

— это доля нац. дохода j-той
страны, кот-я тратится на закупку товаров
в i-той
стране.

= 1

C
элементами

составим матрицу:А =

– структурная матрица международной
торговли

Сумма элементов
по столбцам равна 1

Сумма элементов
по строкам:

+ … +

– все то, что покупают у i-той
страны => выручка i-той
страны в этой торговле.

не может
быть больше, чем

(доход)

=> АХ
= Х Х =

Для бездефицитности
торговли нац. доходы стран должны быть
коорд-ми собственного вектора структурной
матрицы с собственным значением

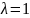
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Занятие 4 (Фдз 5).

Действия с линейными операторами. Образ, ядро, ранг, дефект линейного оператора.

4.1. Умножение линейного оператора на число, сложение линейных операторов, перемножение линейных операторов. Связь указанных действий с соответствующими операциями над матрицами линейных операторов.

4.2. Условие существования обратного отображения к линейному оператору, его свойства. Матрица обратного оператора, ее нахождение по матрице оператора.

4.3. Ядро и образ линейного оператора, их свойства. Ранг и дефект линейного оператора. Критерий обратимости линейного оператора в терминах его ядра, образа, ранга, дефекта.

4.1. Пусть даны два линейных оператора , действующие в одном и том же конечномерном линейном пространстве размерности .

По определению.

1) При умножении линейного оператора на число получается линейный оператор , действующий по правилу: , где .

2) При сложении линейных операторов и получается линейный оператор , действующий по правилу: , где .

3) Произведение линейных операторов и также дает линейный оператор , действующий по правилу .

Аналогично определяется произведение : , где .

Отметим, что и (в общем случае).

Пусть — базис пространства и

— матрицы линейных операторов , в базисе .

Тогда матрицы операторов , , , в базисе находятся так:

— матрица оператора в базисе ;

— — матрица оператора в базисе .

Пример 1. Даны два линейных оператора и :

— оператор поворота векторов на декартовой плоскости (вокруг начала координат против часовой стрелки) на угол ;

— оператор проектирования векторов на ось .

Найти матрицы операторов в базисе , где — единичные векторы на осях .

Решение.

Сначала найдем матрицы операторов в базисе .

— первый столбец матрицы ,

второй столбец матрицы . Следовательно, .

— первый столбец матрицы ,

второй столбец матрицы . Следовательно, .

Обозначим — матрицы операторов в базисе .

Найдем эти матрицы с помощью матриц .

4.2. В случае, когда линейный оператор осуществляет взаимно однозначное отображение линейного пространства на себя, то существует обратный линейный оператор . Если — матрица оператора в базисе пространства , то матрица оператора в этом базисе равна . Следовательно, линейный оператор обратим (имеет обратный оператор ) тогда и только тогда, когда матрица оператора не вырождена (т.е. ).

Пример 2. Выяснить, какие из линейных операторов , примера 1 являются обратимыми?

Решение.

Матрица оператора (в базисе ) равна

. .

Следовательно, матрица не вырождена (отсюда сразу же вытекает, что в любом другом базисе матрица оператора также не вырождена). Оператор обратим, и матрица обратного оператора в базисе равна

Матрица оператора (в базисе ) равна

. .

Следовательно, матрица вырождена (отсюда сразу же вытекает, что в любом другом базисе матрица оператора также вырождена). Оператор не обратим, и обратного оператора не существует.

4.3. Ядром линейного оператора называется множество всех , для которых . Для ядра линейного оператора принято обозначение . Ядро не может быть пустым множеством, т.к. для любого линейного оператора и, значит, нулевой элемент линейного пространства всегда принадлежит множеству .

Образ линейного оператора и ядро этого оператора являются линейными подпространствами в пространстве .

Рангом линейного оператора называется размерность образа этого оператора. Дефектом линейного оператора называется размерность ядра этого оператора. Если , то

Если известна матрица линейного оператора в каком-нибудь базисе , то ранг этого оператора можно найти по рангу матрицы : .

Пример 3. Найти ядро, образ, а также ранг и дефект линейного оператора , где , и оператор действует по правилу

Решение.

. Базис пространства состоит из четырех многочленов. Например, многочлены , , , образуют базис .

Найдем образ оператора .

— линейная оболочка трех многочленов . Эти многочлены представляют полную линейно независимую систему в . Следовательно, — базис . Значит, — ранг оператора .

— дефект оператора .

Найдем ядро оператора . Ядро состоит из тех многочленов , для которых .

Многочлен тождественно равен нулю (т.е. для всех ) тогда и только тогда, когда коэффициенты при всех степенях равны нулю.

Следовательно, .

Таким образом, ядро образует множество всех постоянных многочленов.

— одномерное линейное пространство (его базисом служит ) . Этот результат подтверждает ранее найденное значение дефекта оператора.

Ранг оператора можно получить другим способом. Найдем матрицу оператора в базисе , , , пространства .

— первый столбец матрицы .

— второй столбец матрицы .

— третий столбец матрицы .

— четвертый столбец матрицы .

. Ранг этой матрицы равен трем. Следовательно, .

Пример 4. Найти образ, ядро, ранг и дефект линейного оператора , где , и оператор действует по правилу , где .

Решение.

Стандартным базисом пространства служит система матриц .

Найдем образ оператора .

, где — произвольное число (в силу произвольности чисел ). Следовательно,

— одномерная линейная оболочка с базисом .

— ранг , — дефект .

Найдем ядро оператора . Нулевым элементом пространства является нулевая матрица.

Общее решение полученной системы из одного уравнения с четырьмя неизвестными (если считать свободными неизвестными) записать в виде

, где .

— линейная оболочка с базисом .

Вычислим теперь ранг оператора по матрице этого оператора. Матрицу оператора проще всего найти в базисе пространства .

— первый столбец матрицы .

— второй столбец матрицы .

— третий столбец матрицы .

— четвертый столбец матрицы .

Матрица получена из матрицы так: ко 2-й строке матрицы прибавили 3-ю строку.

Ранги матриц и одинаковы. .

___________________________________________________________________________

Домашнее задание.

1. Даны два линейных оператора , действующие в пространстве .

— оператор поворота векторов плоскости против часовой стрелки вокруг начала координат на угол .

— оператор проектирования векторов плоскости на прямую .

Найти матрицы операторов в базисе . Указать, какие из операторов имеют обратный оператор?

2. Найти ядро, образ, ранг и дефект линейного оператора

, .

Допускает ли данный оператор обратный оператор ?

3. Найти ядро, образ, ранг и дефект линейного оператора ,

действующего в линейном пространстве .

Источник