Как найти матрицу перестановки - Исправление недочетов и поиск решений вместе с Examum.ru

From Wikipedia, the free encyclopedia

In mathematics, particularly in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry of 1 in each row and each column and 0s elsewhere. Each such matrix, say P, represents a permutation of m elements and, when used to multiply another matrix, say A, results in permuting the rows (when pre-multiplying, to form PA) or columns (when post-multiplying, to form AP) of the matrix A.

Definition[edit]

Given a permutation π of m elements,

pi :lbrace 1,ldots ,mrbrace to lbrace 1,ldots ,mrbrace

represented in two-line form by

${begin{pmatrix}1&2&cdots &m\pi (1)&pi (2)&cdots &pi (m)end{pmatrix}},$

there are two natural ways to associate the permutation with a permutation matrix; namely, starting with the m × m identity matrix, I_m, either permute the columns or permute the rows, according to π. Both methods of defining permutation matrices appear in the literature and the properties expressed in one representation can be easily converted to the other representation. This article will primarily deal with just one of these representations and the other will only be mentioned when there is a difference to be aware of.

The m × m permutation matrix P_π = (p_ij) obtained by permuting the columns of the identity matrix I_m, that is, for each i, p_ij = 1 if j = π(i) and p_ij = 0 otherwise, will be referred to as the column representation in this article.^[1] Since the entries in row i are all 0 except that a 1 appears in column π(i), we may write

$P_{pi }={begin{bmatrix}{mathbf e}_{{pi (1)}}\{mathbf e}_{{pi (2)}}\vdots \{mathbf e}_{{pi (m)}}end{bmatrix}},$

where ${mathbf e}_{j}$ , a standard basis vector, denotes a row vector of length m with 1 in the jth position and 0 in every other position.^[2]

For example, the permutation matrix P_π corresponding to the permutation ${displaystyle pi ={begin{pmatrix}1&2&3&4&5\1&4&2&5&3end{pmatrix}}}$ is

$P_{pi }={begin{bmatrix}{mathbf {e}}_{{pi (1)}}\{mathbf {e}}_{{pi (2)}}\{mathbf {e}}_{{pi (3)}}\{mathbf {e}}_{{pi (4)}}\{mathbf {e}}_{{pi (5)}}end{bmatrix}}={begin{bmatrix}{mathbf {e}}_{{1}}\{mathbf {e}}_{{4}}\{mathbf {e}}_{{2}}\{mathbf {e}}_{{5}}\{mathbf {e}}_{{3}}end{bmatrix}}={begin{bmatrix}1&0&0&0&0\0&0&0&1&0\0&1&0&0&0\0&0&0&0&1\0&0&1&0&0end{bmatrix}}.$

Observe that the jth column of the I₅ identity matrix now appears as the π(j)th column of P_π.

The other representation, obtained by permuting the rows of the identity matrix I_m, that is, for each j, p_ij = 1 if i = π(j) and p_ij = 0 otherwise, will be referred to as the row representation.

Properties[edit]

The column representation of a permutation matrix is used throughout this section, except when otherwise indicated.

Multiplying $P_{{pi }}$ times a column vector g will permute the rows of the vector:

${displaystyle P_{pi }mathbf {g} ={begin{bmatrix}mathbf {e} _{pi (1)}\mathbf {e} _{pi (2)}\vdots \mathbf {e} _{pi (n)}end{bmatrix}}{begin{bmatrix}g_{1}\g_{2}\vdots \g_{n}end{bmatrix}}={begin{bmatrix}g_{pi (1)}\g_{pi (2)}\vdots \g_{pi (n)}end{bmatrix}}.}$

Repeated use of this result shows that if M is an appropriately sized matrix, the product, ${displaystyle P_{pi }M}$ is just a permutation of the rows of M. However, observing that

${displaystyle P_{pi }mathbf {e} _{k}^{mathsf {T}}=mathbf {e} _{pi ^{-1}(k)}^{mathsf {T}}}$

for each k shows that the permutation of the rows is given by π⁻¹. ( ${displaystyle M^{mathsf {T}}}$ is the transpose of matrix M.)

As permutation matrices are orthogonal matrices (that is, ${displaystyle P_{pi }P_{pi }^{mathsf {T}}=I}$ ), the inverse matrix exists and can be written as

${displaystyle P_{pi }^{-1}=P_{pi ^{-1}}=P_{pi }^{mathsf {T}}.}$

Multiplying a row vector h times $P_{{pi }}$ will permute the columns of the vector:

${displaystyle mathbf {h} P_{pi }={begin{bmatrix}h_{1}&h_{2}&cdots &h_{n}end{bmatrix}}{begin{bmatrix}mathbf {e} _{pi (1)}\mathbf {e} _{pi (2)}\vdots \mathbf {e} _{pi (n)}end{bmatrix}}={begin{bmatrix}h_{pi ^{-1}(1)}&h_{pi ^{-1}(2)}&cdots &h_{pi ^{-1}(n)}end{bmatrix}}}$

Again, repeated application of this result shows that post-multiplying a matrix M by the permutation matrix P_π, that is, M P_π, results in permuting the columns of M. Notice also that

${displaystyle mathbf {e} _{k}P_{pi }=mathbf {e} _{pi (k)}.}$

Given two permutations π and σ of m elements, the corresponding permutation matrices P_π and P_σ acting on column vectors are composed with

${displaystyle P_{sigma }P_{pi },mathbf {g} =P_{pi ,circ ,sigma },mathbf {g} .}$

The same matrices acting on row vectors (that is, post-multiplication) compose according to the same rule

${displaystyle mathbf {h} P_{sigma }P_{pi }=mathbf {h} P_{pi ,circ ,sigma }.}$

To be clear, the above formulas use the prefix notation for permutation composition, that is,

Let ${displaystyle Q_{pi }}$ be the permutation matrix corresponding to π in its row representation. The properties of this representation can be determined from those of the column representation since ${displaystyle Q_{pi }=P_{pi }^{mathsf {T}}=P_{{pi }^{-1}}.}$ In particular,

${displaystyle Q_{pi }mathbf {e} _{k}^{mathsf {T}}=P_{{pi }^{-1}}mathbf {e} _{k}^{mathsf {T}}=mathbf {e} _{(pi ^{-1})^{-1}(k)}^{mathsf {T}}=mathbf {e} _{pi (k)}^{mathsf {T}}.}$

From this it follows that

${displaystyle Q_{sigma }Q_{pi },mathbf {g} =Q_{sigma ,circ ,pi },mathbf {g} .}$

Similarly,

${displaystyle mathbf {h} ,Q_{sigma }Q_{pi }=mathbf {h} ,Q_{sigma ,circ ,pi }.}$

Permutation matrices can be characterized as the orthogonal matrices whose entries are all non-negative.^[3]

Matrix group[edit]

If (1) denotes the identity permutation, then P₍₁₎ is the identity matrix.

Let S_n denote the symmetric group, or group of permutations, on {1,2,…,n}. Since there are n! permutations, there are n! permutation matrices. By the formulas above, the n × n permutation matrices form a group under matrix multiplication with the identity matrix as the identity element.

The map S_n → GL(n, Z₂) that sends a permutation to its column representation is a faithful representation.

Doubly stochastic matrices[edit]

A permutation matrix is itself a doubly stochastic matrix, but it also plays a special role in the theory of these matrices. The Birkhoff–von Neumann theorem says that every doubly stochastic real matrix is a convex combination of permutation matrices of the same order and the permutation matrices are precisely the extreme points of the set of doubly stochastic matrices. That is, the Birkhoff polytope, the set of doubly stochastic matrices, is the convex hull of the set of permutation matrices.^[4]

Linear algebraic properties[edit]

The trace of a permutation matrix is the number of fixed points of the permutation. If the permutation has fixed points, so it can be written in cycle form as π = (a₁)(a₂)…(a_k)σ where σ has no fixed points, then e_a₁,e_a₂,…,e_{a_k} are eigenvectors of the permutation matrix.

To calculate the eigenvalues of a permutation matrix ${displaystyle P_{sigma }}$ , write sigma as a product of cycles, say, ${displaystyle sigma =C_{1}C_{2}cdots C_{t}}$ . Let the corresponding lengths of these cycles be ${displaystyle l_{1},l_{2}...l_{t}}$ , and let ${displaystyle R_{i}(1leq ileq t)}$ be the set of complex solutions of ${displaystyle x^{l_{i}}=1}$ . The union of all $R_{i}$ s is the set of eigenvalues of the corresponding permutation matrix. The geometric multiplicity of each eigenvalue equals the number of $R_{i}$ s that contain it.^[5]

From group theory we know that any permutation may be written as a product of transpositions. Therefore, any permutation matrix P factors as a product of row-interchanging elementary matrices, each having determinant −1. Thus, the determinant of a permutation matrix P is the signature of the corresponding permutation.

Examples[edit]

Permutation of rows and columns[edit]

When a matrix M is multiplied by a permutation matrix P on the left to make PM, the product is the result of permuting the rows of M. As a special case, if M is a column vector, then PM is the result of permuting the entries of M:

P · (1, 2, 3, 4)^T = (4, 1, 3, 2)^T

When instead M is multiplied by a permutation matrix on the right to make MP, the product is the result of permuting the columns of M. As a special case, if M is a row vector, then MP is the result of permuting the entries of M:

(1, 2, 3, 4) · P = (2, 4, 3, 1)

Permutation of rows[edit]

The permutation matrix P_π corresponding to the permutation ${displaystyle pi ={begin{pmatrix}1&2&3&4&5\1&4&2&5&3end{pmatrix}}}$ is

Given a vector g,

$P_{pi }{mathbf {g}}={begin{bmatrix}{mathbf {e}}_{{pi (1)}}\{mathbf {e}}_{{pi (2)}}\{mathbf {e}}_{{pi (3)}}\{mathbf {e}}_{{pi (4)}}\{mathbf {e}}_{{pi (5)}}end{bmatrix}}{begin{bmatrix}g_{1}\g_{2}\g_{3}\g_{4}\g_{5}end{bmatrix}}={begin{bmatrix}g_{1}\g_{4}\g_{2}\g_{5}\g_{3}end{bmatrix}}.$

Explanation[edit]

A permutation matrix will always be in the form

${begin{bmatrix}{mathbf {e}}_{{a_{1}}}\{mathbf {e}}_{{a_{2}}}\vdots \{mathbf {e}}_{{a_{j}}}\end{bmatrix}}$

where e_{a_i} represents the ith basis vector (as a row) for R^j, and where

${begin{bmatrix}1&2&ldots &j\a_{1}&a_{2}&ldots &a_{j}end{bmatrix}}$

is the permutation form of the permutation matrix.

Now, in performing matrix multiplication, one essentially forms the dot product of each row of the first matrix with each column of the second. In this instance, we will be forming the dot product of each row of this matrix with the vector of elements we want to permute. That is, for example, v = (g₀,…,g₅)^T,

e_{a_i}·v = g_{a_i}

So, the product of the permutation matrix with the vector v above, will be a vector in the form (g_a₁, g_a₂, …, g_{a_j}), and that this then is a permutation of v since we have said that the permutation form is

${begin{pmatrix}1&2&ldots &j\a_{1}&a_{2}&ldots &a_{j}end{pmatrix}}.$

So, permutation matrices do indeed permute the order of elements in vectors multiplied with them.

Restricted forms[edit]

Costas array, a permutation matrix in which the displacement vectors between the entries are all distinct
n-queens puzzle, a permutation matrix in which there is at most one entry in each diagonal and antidiagonal

References[edit]

Brualdi, Richard A. (2006). Combinatorial matrix classes. Encyclopedia of Mathematics and Its Applications. Vol. 108. Cambridge: Cambridge University Press. ISBN 0-521-86565-4. Zbl 1106.05001.
Joseph, Najnudel; Ashkan, Nikeghbali (2010), The Distribution of Eigenvalues of Randomized Permutation Matrices, arXiv:1005.0402, Bibcode:2010arXiv1005.0402N

Источник

Содержание

1 Матрица перестановок
- 1.1 Элементарная матрица перестановок
- 1.2 Пример
- 1.3 Применение
2 Свойства
3 См. также
4 Источники информации

Матрица перестановок

Определение:

Матрица перестановок (англ. Permutation matrix) — квадратная бинарная матрица, в каждой строке и в каждом столбце которой находится лишь одна единица.

Каждая матрица перестановки размера является матричным представлением перестановки порядка .

Пусть дана перестановка порядка :

Соответствующей матрицей перестановки является матрица вида:

, где — двоичный вектор длины , -й элемент которого равен единице, а остальные равны нулю.

Элементарная матрица перестановок

Определение:

Если матрица перестановок получена из единичной матрицы перестановкой местами двух строк (или двух столбцов), то такая матрица называется элементарной матрицей перестановок (англ. Elementary permutation matrix).

Пример

Пусть дана перестановка: . В соответствующей матрице в первом столбце единица будет стоять на первом месте, во втором столбе
на третьем месте, в третьем на втором. Итого: . Также эта матрица является элементарной матрицей перестановок, так как получена из единичной, перестановкой второго и третьего столбцов.

Применение

Благодаря своим свойствам, матрицам перестановок нашлось применение в линейной алгебре. Они используются в элементарных преобразованиях матриц, то есть домножение слева или справа на матрицу перестановок, есть перестановка любых строк или столбов соответственно.

Свойства

Утверждение:

Для любых двух перестановок их матрицы обладают свойством:

где — операция умножения перестановок.

Рассмотрим . Эта сумма может быть равна нулю или единице, причем единице в том случае, если в -той строчке на -том столбце матрицы и в -той строчке на -том столбце матрицы стоят единицы. значит, что в перестановке на -том месте стоит элемент , и означает что в перестановке на -том месте стоит элемент , а означает что в перестановке, которой соответствует эта матрица, так же на -том месте стоит элемент . Но также известно, что . В результате если , то . Аналогичные рассуждения можно провести когда , и также получим, что . Поэтому для любых справедливо , а раз такое равентсво выполняется, то .

Утверждение:

Для любой матрицы перестановок справедливо:

где — единичная матрица.

Рассмотрим

Теперь в обратную сторону
где — символ Кронекера.

Отсюда следует, что , так как по определению обратной матрицы .

Утверждение:

При умножение слева матрицы перестановок на матрицу происходит перестановка -й и -й строк матрицы .
Умножение справа матрицы перестановок на матрицу приводит к перестановке -го и -го столбцов матрицы .

Рассмотрим сначала умножение слева, т.е. матрицу , которую обозначим . Посчитаем чему равны элементы этой матрицы:

Действительно, по определению матрицы перестановок единица в строке стоит на -м месте, если , , на -м месте, если , и на -м месте, если . Итак, если , то -я строка матрицы просто совпадает с -й строкой
матрицы . Далее, -я строка матрицы совпадает с -й строкой матрицы , и
наоборот. Поэтому получается из перестановкой -й и -й строк.

Теперь рассмотрим умножение справа. Пусть .

По определению матрицы перестановок единица в столбце стоит на -м месте, если , на -м месте,
если , и на -м месте, если .
Итак, если , то -й столбец матрицы просто совпадает с -м столбцом
матрицы . Далее, -й столбец матрицы совпадает с -м столбцом матрицы , и

наоборот. Поэтому получается из перестановкой -го и -го столбцов.

Пример

Пусть задана матрица перестановки , которая соответствует перестановке , и матрица ,

тогда перемножив получим:

, видно, что вторая и третья строки поменялись местами.

, видно, что второй и третий столбец поменялись местами.

Утверждение:

Квадрат элементарной матрицы перестановок есть единичная матрица.

Любая элементарная матрица перестановок является симметричной матрицей, следовательно . Отсюда следует, что

, а .

Утверждение:

Матрица перестановок -го порядка может быть представлена в виде произведения элементарных матриц перестановок .

Обозначим — элементарную матрицу, полученную из единичной путем изменения -й и -й строк. Рассмотрим матрицу перестановок

Возьмем и перестановками строк (домножением соответствующей элементарной матрицей слева) или столбцов (домножением соответствующей элементарной матрицей справа) перемещаем его на первое место. Так как в каждой строке или столбце только одна единица, то получим: и так далее, пока не получится единичной матрицы.

В итоге: .

Все элементарные матрицы обратимы и обратная к элементарной матрице — это тоже элементарная матрица, следовательно: .

Заметим, что с каждым шагом мы домножаем на одну элементарную матрицу перестановок, следовательно всего будет таких матриц.

См. также

Умножение перестановок, обратная перестановка, группа перестановок

Источники информации

Википедия — Матрица перестановки
Матрица перестановки
Wikipedia — Permutation matrix
Brualdi, Richard A. (2006). Combinatorial matrix classes. Encyclopedia of Mathematics and Its Applications. Cambridge: Cambridge University Press. стр. 2, 19.

Источник

Если в единичной матрице изменить порядок расположения строк, то полученная матрица называется матрицей перестановок. Иначе говоря, квадратная матрица, в каждой строке и в каждом столбце которой только один элемент отличен от нуля и равен единице, называется матрицей перестановок.

Непосредственным вычислением легко проверяются следующие свойства матрицы перестановок.

Умножение слева матрицы перестановок на прямоугольную матрицу A приводит к перестановке строк матрицы A.
Умножение справа матрицы перестановок на прямоугольную матрицу A приводит к перестановке столбцов матрицы A.

Пусть, например, пятой строкой матрицы перестановок является строка вида (0, 1, 0, 0, …, 0). Тогда результатом умножения этой строки на столбцы прямоугольной матрицы A = || a_i j || является вторая строка (a₂₁ a₂₂ a₂₃ …) матрицы A, которая располагается в позиции пятой строки результитрующей матрицы.

Таким образом, если в i-ой строке матрицы перестановок P единица расположена в j-ом столбце, то умножение матрицы P слева на матрицу A приводит к перемещению j-ой строки матрицы A в позицию i-ой строки.

Аналогично, если в i-ом столбце матрицы перестановок P единица расположена в j-ой строке, то умножение матрицы P справа на матрицу A приводит к перемещению j-го столбца матрицы A в позицию i-го столбца.

Если матрицы перестановок P получена из единичной матрицы E перестановкой местами двуз строк (или двух столбцов), то такая матрица называется элементарной матрицей перестановок.


При умножение слева элементарной матрицы перестановок на матрицу A происходит перестановка соответствующих строк матрицы A.


Умножение справа элементарной матрицы перестановок на матрицу A приводит к перестановке соответствующих столбцов матрицы A.

Для любой матрицы перестановок P справедливы следующие свойства:

где — транспонированная матрица перестановок; E — единичная матрица.

Действительно,

где — дельта-символ Кронекера.

Терема 1. Произведение матриц перестановок одного и того же порядка есть матрица перестановок.

Терема 2. Матрица перестановок n-го порядка может быть представлена в виде произведения (n — 1) элементарных матриц перестановок.

Терема 3. Квадрат элементарной матрицы перестановок есть единичная матрица.

Доказательство этих утверждений предоставляется читателю.

Источник

Матрица перестановки (или подстановки) — квадратная бинарная матрица, в каждой строке и столбце которой находится лишь один единичный элемент. Каждая матрица перестановки размера является матричным представлением перестановки порядка .

Определение

Пусть дана перестановка порядка :

${displaystyle {begin{pmatrix}1&&2&&ldots &&n\sigma (1)&&sigma (2)&&ldots &&sigma (n)end{pmatrix}}}$

Соответствующей матрицей перестановки является матрица вида:

${displaystyle P_{sigma }={begin{pmatrix}mathbf {e} _{pi (1)}\mathbf {e} _{pi (2)}\vdots \mathbf {e} _{pi (n)}end{pmatrix}}}$

Где ${displaystyle mathbf {e} _{i}}$ — арифметический вектор длины , -й элемент которого равен 1, а остальные равны нулю.

Пример

Перестановка: ${displaystyle pi ={begin{pmatrix}1&&2&&3&&4\4&&2&&1&&3end{pmatrix}}}$

Соответствующая матрица:

${displaystyle P={begin{pmatrix}0&&0&&0&&1\0&&1&&0&&0\1&&0&&0&&0\0&&0&&1&&0\end{pmatrix}}}$

Свойства

Для любых двух перестановок их матрицы обладают свойством:

${displaystyle P_{sigma }P_{pi }=P_{sigma circ pi }}$

Матрицы перестановки ортогональны, так что для каждой такой матрицы существует обратная:

${displaystyle P_{sigma }^{-1}=P_{sigma }^{T}}$

Умножение произвольной матрицы на перестановочную соответственно меняет местами её строки.

Умножение перестановочной матрицы на произвольную меняет местами столбцы в .

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Матрица перестановки. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

Источник

Ма́трица
перестано́вки (или подстано́вки)
— квадратная бинарная
матрица,
в каждой строке и столбце которой
находится лишь один единичный элемент.
Каждая матрица перестановки
размера
является
матричным представлением перестановки порядка
.

Определение

Пусть
дана перестановка
порядка
:

Соответствующей
матрицей перестановки является
матрица
вида:

где
— вектор длины
,
-й
элемент которого равен 1, а остальные
равны нулю.

Пример

Перестановка:

Соответствующая
матрица:

Свойства

Для
любых двух перестановок
их
матрицы обладают свойством:

Матрицы
перестановки ортогональны,
так что для каждой такой матрицы
существует обратная:

Умножение
произвольной матрицы
на
перестановочную соответственно меняет
местами её столбцы.
Умножение
перестановочной матрицы на
произвольную
меняет
местами строки в
.

Вопрос 39.Решение системы линейных алгебраических уравнений методом Гаусса с выбором главного элемента по столбцам Метод Гаусса с выбором главного элемента

Метод
Гаусса с выбором главного элемента по
столбцам, в этом случае на каждом этапе
прямого хода строки матрицы переставляются
таким образом, чтобы диагональный
угловой элемент был максимальным. При
исключении соответствующего неизвестного
из других строк деление будет производиться
на наибольший из возможных коэффициентов
и, как следовательно, относительная
погрешность будет наименьшей. Обратный
ход происходит так же, как и в классическом
методе Гаусса.

Вопрос 40.Решение системы линейных алгебраических уравнений методом вращения Метод вращения

Как
и в методе Гаусса, цель прямого хода
преобразований в этом методе–приведение
системы к треугольному виду последовательным
обнулением поддиагональных элементов
сначала первого столбца, затем второго
и т.д.

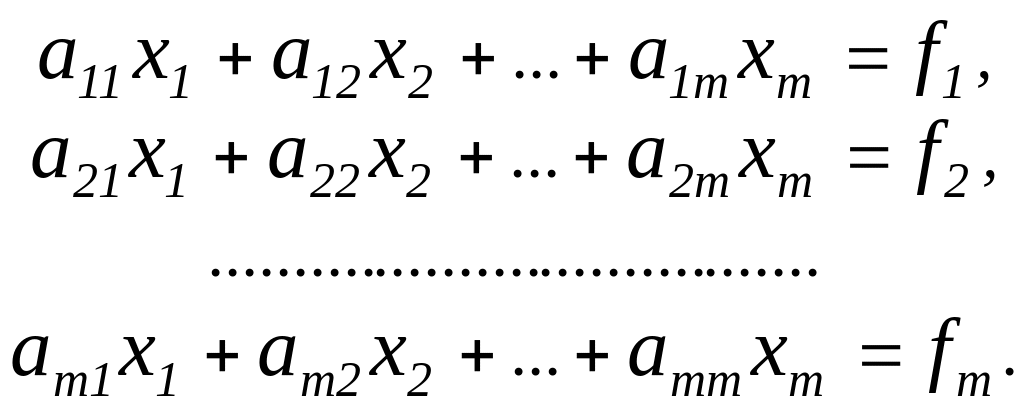
Умножим первое уравнение исходной
системы (1) на с₁ ,второе
на s₁ и сложим их ; полученным
уравнением заменим первое уравнение
системы. Затем первое уравнение исходной
системы умножаем на –s₁ ,
второе на c₁
и результатом их сложения заменим
второе уравнение . Таким образом, первые
два уравнения (1) заменяются уравнениями

Отсюда

.
Эти числа можно интерпретировать как
косинус и синус некоторого угла

(отсюда
название метод вращения, каждый
шаг такого преобразования можно
рассматривать как вращение расширенной
матрицы системы в плоскости обнуляемого
индекса).

В результате преобразований получим
систему

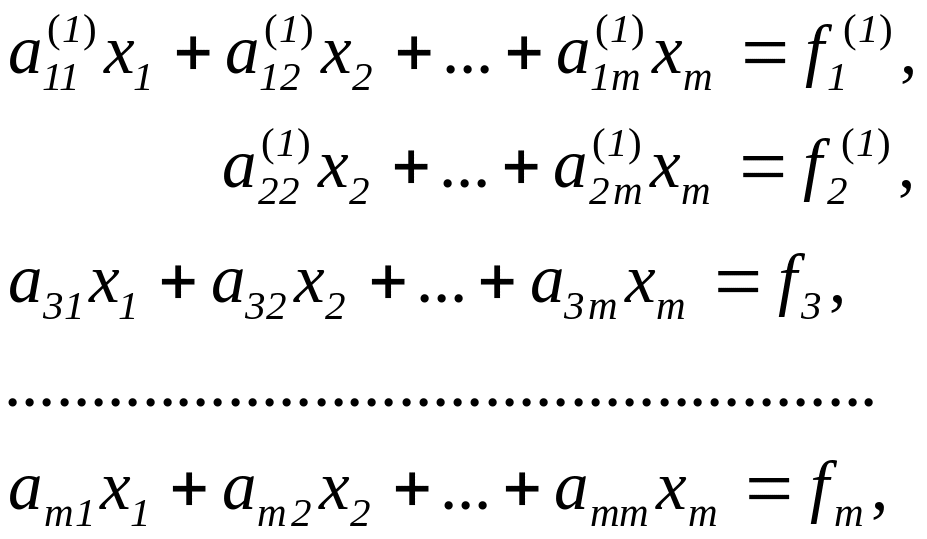
где

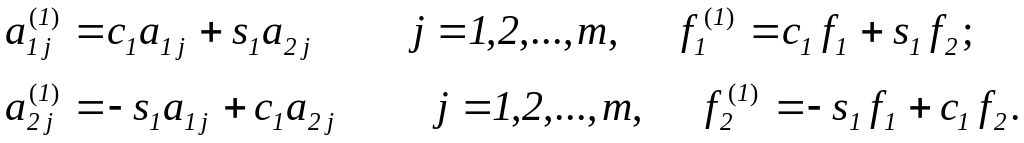
Далее
первое уравнение системы заменяется
новым, полученным сложением результатов
умножения первого и третьего уравнений
соответственно на

а
третье–уравнением, полученное при
сложении результатов умножения тех
же

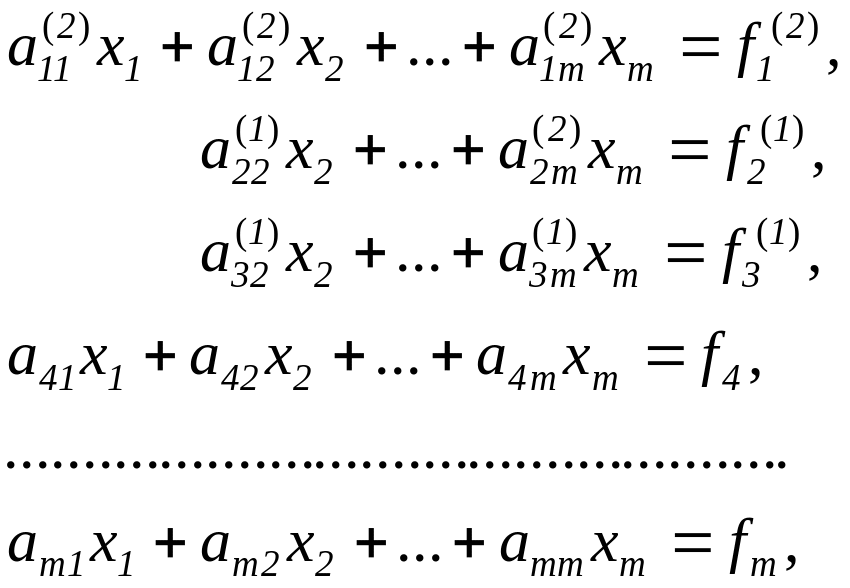
где

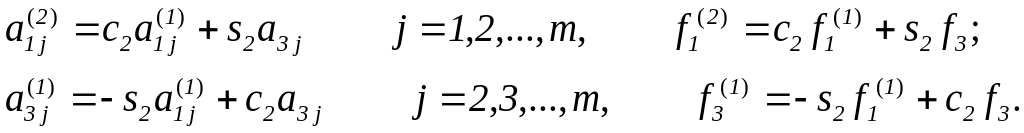
Выполнив
преобразование m-1 раз, придем к
системе

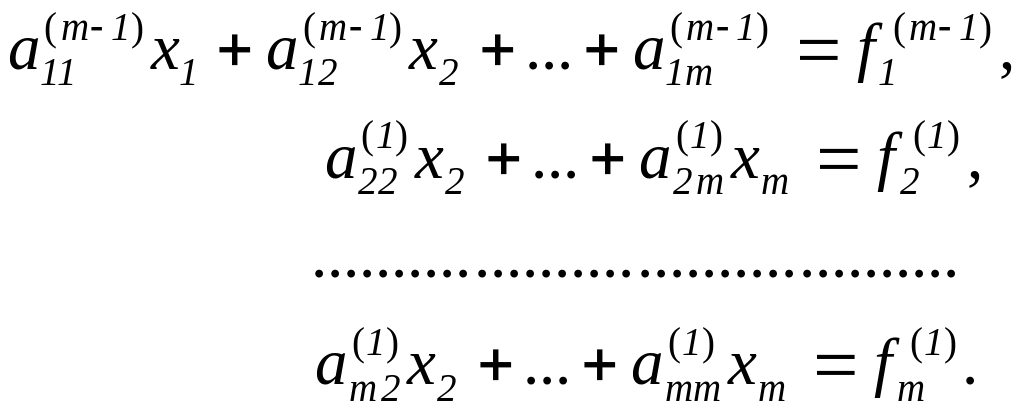
Вид полученной системы такой же, как
после первого этапа преобразований
методом Гаусса. Эта система обладает
следующим свойством: длина любого
вектора-столбца (эвклидова норма)
расширенной матрицы остается такой же,
как у исходной матрицы. Следовательно,
при выполнении преобразований не
наблюдается рост элементов.

Далее по этому же алгоритму преобразуется
матрица

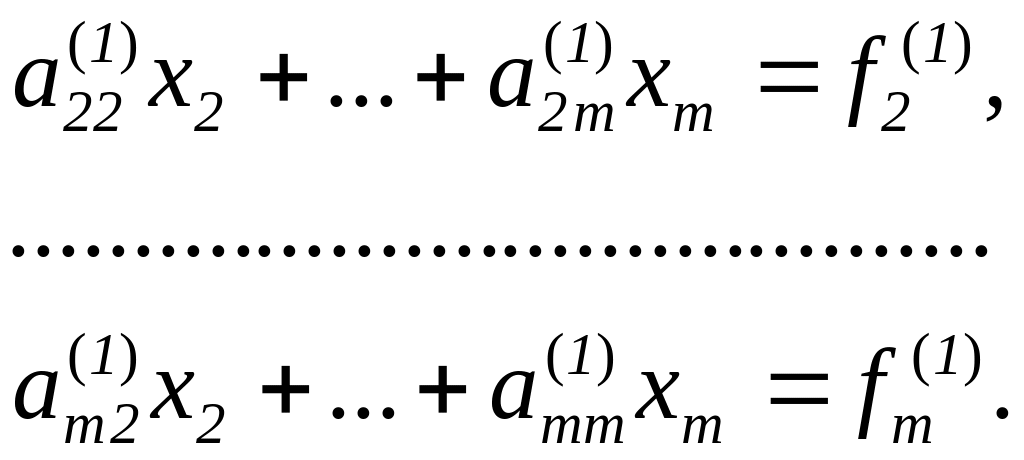
и т.д.

В результате m-1 этапов прямого хода
система будет приведена к треугольному
виду.

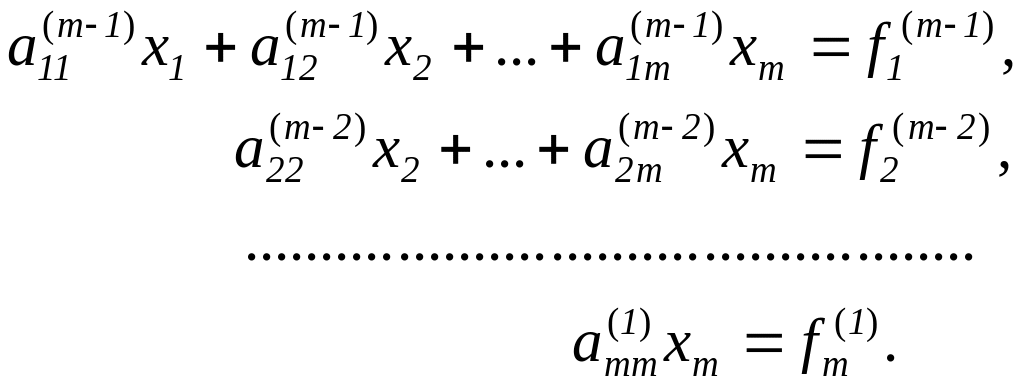
Нахождение неизвестных не отличается
от обратного хода метода Гаусса.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Definition[edit]

Properties[edit]

Matrix group[edit]

Doubly stochastic matrices[edit]

Linear algebraic properties[edit]

Examples[edit]

Permutation of rows and columns[edit]

Permutation of rows[edit]

Explanation[edit]

Restricted forms[edit]

See also[edit]

References[edit]

Содержание

Матрица перестановок

Элементарная матрица перестановок

Пример

Применение

Свойства

См. также

Источники информации

Определение

Пример

Свойства

Определение

Свойства

Вопрос 39.Решение системы линейных алгебраических уравнений методом Гаусса с выбором главного элемента по столбцам Метод Гаусса с выбором главного элемента

Вопрос 40.Решение системы линейных алгебраических уравнений методом вращения Метод вращения