Как найти матрицу преобразования пространства

Линейные операторы (преобразования)

Определение линейных операторов (преобразований)

Линейным преобразованием (линейным оператором) линейного пространства называется линейное отображение пространства в себя.

Поскольку линейное преобразование является частным случаем линейного отображения, к нему применимы все понятия и свойства, рассмотренные для отображений: инъективность, сюръективность, биективность, обратимость, ядро, образ, дефект, ранг и т.д.

Матрицей линейного оператора (преобразования) в базисе пространства называется квадратная матрица , составленная из координатных столбцов образов базисных векторов , найденных относительно базиса .

Матрица биективного линейного оператора (преобразования) обратима, т.е. невырождена. Поэтому биективное (обратимое) преобразование называют также невырожденным.

---

Примеры линейных операторов (преобразований)

1. Обозначим — нулевое преобразование n-мерного пространства , которое ставит в соответствие любому вектору нулевой элемент пространства . Это преобразование не является инъективным, сюръективным, биективным, обратимым. Матрица нулевого преобразования (в любом базисе) нулевая, ядро преобразования , образ преобразования , дефект , ранг .

2. Обозначим — тождественное преобразование n-мерного пространства , которое ставит в соответствие каждому вектору этот же вектор . Это преобразование является инъективным, сюръективным, биективным, обратимым. Матрица тождественного преобразования (в любом базисе) единичная n-го порядка, ядро преобразования , образ преобразования , дефект , ранг .

3. Обозначим — центральную симметрию n-мерного пространства (относительно нулевого вектора ), т.е. преобразование, которое каждому вектору ставит в соответствие противоположный ему вектор: . Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Матрица преобразования противоположна единичной (в любом базисе): ; ядро преобразования , образ преобразования , дефект , ранг .

4. Обозначим — гомотетию n-мерного пространства (с коэффициентом ), т.е. преобразование, которое каждому вектору ставит в соответствие коллинеарный ему вектор: . Это преобразование линейное. При оно инъективное, сюръективное, биективное, обратимое. Матрица преобразования пропорциональна единичной (в любом базисе): , ядро преобразования , образ преобразования , дефект , ранг . При (см. пункт 1); при (см. пункт 2); при (см. пункт 3).

5. Рассмотрим линейное пространство радиус-векторов (с общим началом в точке ), принадлежащих одной плоскости (рис. 9.1). Обозначим — поворот вокруг точки (на угол в положительном направлении (против часовой стрелки)). Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Найдем матрицу поворота в стандартном ортонормированием базисе . Раскладывая образы базисных векторов по базису, получаем

Составляем матрицу (9.1) преобразования (оператора), записывая найденные координаты образов по столбцам:

Ядро оператора (преобразования) , образ преобразования , дефект , ранг . При (см. пункт 2); при (см. пункт 3).

6. Обозначим — оператор дифференцирования, который каждому многочлену степени не выше и ставит в соответствие его производную, рассматриваемую как многочлен степени не выше . Это преобразование линейное, неинъективное, несюръективное, небиективное, необратимое. Квадратная матрица ((n+l)-го порядка) преобразования в стандартном базисе имеет вид

Ядро преобразования — пространство многочленов нулевой степени, образ — пространство многочленов степени не выше , дефект , ранг .

Рассмотрим преобразование линейного пространства тригонометрических многочленов (частоты ) с действительными коэффициентами: , т.е. — множество функций вида , где . Заметим, что это множество является двумерным вещественным линейным пространством. Стандартный базис пространства образуют функции , поскольку они линейно независимы (тождественное равенство нулю возможно только в тривиальном случае ). При дифференцировании функции получаем функцию того же вида. Следовательно, преобразование определено. Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Найдем матрицу преобразования в стандартном базисе . Раскладывая образы базисных векторов, получаем

Составляем матрицу (9.1) преобразования, записывая найденные координаты образов по столбцам: . Ядро преобразования — нулевое подпространство, образ , дефект , ранг , .

Аналогичными свойствами обладает преобразование , где — множество функций вида с комплексными коэффициентами и . Множество является двумерным комплексным линейным пространством.

7. Пусть линейное пространство разлагается в прямую сумму подпространств . Обозначим — оператор проектирования на подпространство параллельно подпространству , который каждому вектору , где , ставит в соответствие его составляющую (проекцию) , т.е. (рис.9.2). Это преобразование линейное. При оно неинъективное, несюръективное, небиективное, необратимое. Ядро преобразования , образ преобразования , дефект , Ранг ,. При ; при .

8. Пусть линейное пространство разлагается в прямую сумму подпространств . Обозначим — оператор отражения в подпространстве параллельно подпространству (или преобразование симметрии относительно подпространства параллельно подпространству ), который каждому вектору , где , ставит в соответствие вектор , т.е. (рис. 9.3). Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Ядро преобразования , образ преобразования , дефект , ранг . При .

---

Матрицы линейного оператора (преобразования) в разных базисах

Найдем связь матриц одного и того же линейного оператора (преобразования) в разных базисах.

Пусть в базисе преобразование имеет матрицу , а в базисе — матрицу . Если — матрица перехода от базиса к базису , то

Докажем формулу (9.4). Пусть векторы и в базисах и имеют координатные столбцы и соответственно. Если , то по формуле (9.2) имеем

Подставляя в первое равенство связи координат векторов в разных базисах получаем или, учитывая обратимость матрицы . Сравнивая последнее равенство с , убеждаемся в справедливости (9.4).

Замечания 9.2

1. Матрицы линейного преобразования в разных базисах оказываются подобными. И наоборот, любые две подобные матрицы являются матрицами некоторого линейного преобразования, найденными относительно разных базисов.

2. Для матриц преобразований справедливы свойства, рассмотренные ранее. В частности, при фиксированном базисе матрица суммы преобразований равна сумме их матриц, матрица произведения преобразования на число равна произведению матрицы преобразования на это же число, матрица композиции преобразований равна произведению матриц преобразований, матрица обратного преобразования является обратной для матрицы обратимого преобразования.

---

Алгебра линейных операторов (преобразований)

Рассмотрим множество — линейных преобразований (операторов) n-мерного линейного пространства . Напомним, что два преобразования и называются равными, если .

На множестве определены две линейные операции: сложение преобразований и умножение преобразования на число, поскольку в результате этих операций получается линейное преобразование.

Нетрудно показать, что эти операции удовлетворяют условиям:

1. ;

2. ;

3. существует нулевое преобразование такое, что ;

4. для каждого преобразования существует противоположное преобразование такое, что ;

5. и любого числа ;

6. и любых чисел ;

7. и любых чисел ;

8. .

В условиях 5-7 говорится о числах из того же числового поля, над которым определено линейное пространство .

Условия 1-8 повторяют аксиомы линейного пространства. Поэтому множество с линейными операциями является линейным пространством. Если пространство вещественное (комплексное), то и пространство вещественное (комплексное).

Найдем размерность пространства . При фиксированном базисе имеется взаимно однозначное соответствие между линейными преобразованиями и их матрицами, причем это соответствие сохраняет линейные операции. Следовательно, пространство изоморфно пространству — квадратных матриц n-го порядка. Размерность пространства равна . По теореме 8.3:

то есть

Кроме линейных операций в множестве определена операция умножения элементов. Произведением преобразований и назовем их композицию, т.е. . В результате композиции линейных преобразований получается линейное преобразование. Операция умножения удовлетворяет следующим условиям:

1. ;

2. ;

3. ;

4. существует тождественное преобразование такое, что .

Первое условие выражает ассоциативность операции умножения, условия 2 и 3 — законы дистрибутивности, условие 4 — существование нейтрального элемента. Множество с операциями сложения и умножения элементов является кольцом с единицей (вообще говоря, некоммутативное, так как в общем случае ).

Операции умножения операторов (преобразований) и произведения операторов на число (из заданного числового поля) удовлетворяют условию:

5.

Линейное пространство, которое является кольцом, удовлетворяющим условию 5, называется алгеброй. Поэтому множество называют алгеброй линейных операторов (преобразований).

---

Многочлены от линейного оператора (преобразования)

В алгебре можно определить целую неотрицательную степень оператора , полагая по определению

Пусть — многочлен переменной . Многочленом от линейного преобразования называется преобразование .

Многочлен называется аннулирующим для линейного преобразования , если — нулевое преобразование. Заметим, что у каждого линейного преобразования n-мерного линейного пространства существует аннулирующий многочлен степени не выше . Действительно, система из элементов линейного пространства линейно зависима (так как ). Поэтому существуют такие числа , не все равные нулю одновременно, что . Следовательно, многочлен — аннулирующий для преобразования .

---

Замечания 9.3

1. При фиксированном базисе каждому преобразованию (оператору) можно сопоставить его матрицу. Свойства линейных операций 1-8, записанные для матриц преобразований, повторяют свойства линейных операций с матрицами, а свойствам 1-5 произведения операторов отвечают свойства операции умножения матриц.

2. При фиксированном базисе многочлен от линейного преобразования имеет матрицу , где — матрица преобразования в том же базисе. Поэтому свойства многочленов от матриц переносятся на многочлены от линейного преобразования. В частности, многочлены от одного преобразования перестановочны:

3. Функции от матриц определяются при помощи многочленов от матриц. Поэтому можно определить функции от линейных преобразований.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

239

ЛА: Глава 10

При
рассмотрении
—
мерных векторных пространств

мы использовали векторные выражения,
в которых с векторами производилось
некоторое воздействие:

▫ переход
от системы
векторов

к системе
векторов
:

=·,
где

— матрица перехода от базиса

к базису
;

▫ преобразование
строки
координат
b=(,,…,)
вектора

базе

в строку координат b‘
=(,,…,)
этого
же вектора
в базе
:

·=,
или в виде:
=·.

Эти
воздействия производятся на векторы
пространства

не явно, как бы косвенно. Например,
координаты вектора изменились, потому
что изменилась база пространства
.

В
настоящей главе рассмотрим такое
преобразование линейного пространства,
когда все векторы подвергаются одному
и тому же преобразованию, причём так,
что для любого вектора
—
мерного векторного пространства

можно записать:

→ ;

→ ,

при
этом
,
получаемый после преобразования

вектор

называется образом
вектора
,
который называют прообразом.
Для удобства записи вместо обозначения

будем использовать
,
хотя первое было бы привычнее, по аналогии
с обозначением функции в математическом
анализе.

§ 1. Определение линейного преобразования.

Пусть имеем
—
мерное линейное векторное пространствои все его векторы подвергаются некоторому
преобразованию.
Мы будем рассматривать только линейные
преобразования.

Определение: (10.1)

преобразование линейного векторного пространства называется линейным преобразованием этого пространства, если для любых векторов : 1) =, 2) =, для любого числа из некоторого поля.

Из
определения следует: линейное
преобразование переводит любую линейную
комбинацию данных векторов в линейную
комбинацию (с теми же коэффициентами)
образов этих векторов:

(·+·+
…+·)
=

·+·+…+·.

Рассмотрим
основные свойства линейного преобразования

линейного
векторного
пространства
,
вытекающие из определения линейного
преобразования:

1⁰.
Линейное преобразование

оставляет
неподвижным
нулевой вектор:
0
=
0.
Действительно,
0
=(0·)=0·=
0,
по правилу умножения вектора на число.

2⁰.
Образом вектора, противоположного
заданному
вектору
,
служит вектор, противоположный
для образа
этого вектора
,
то есть:
=–.
Достаточно учесть, что: –=(–1)
и воспользоваться свойством 2)
преобразования
.

3⁰.
Линейное преобразование
,
оставляющее неподвижным всякий вектор

,
а именно:
=
— называют тождественным.

4⁰.
Линейное преобразование
,
отображающее всякий вектор
,
в нулевой вектор, а именно:
=0
— называют нулевым.

Пусть
в линейном
векторном
пространстве

выделена база e=(e₁,e₂,…,e_n).
Всякий вектор

этого пространства можно представить
в виде выражения:
=(b₁,b₂,…,)·=·,
где
числа: b₁,
b₂,…,

— координаты вектора

в базе
.
Заметим также, что в выражении:
=·
используется матрица-столбец базы
.

Так
как линейное преобразование
,
по определению, формирует вектор
,
принадлежащий исходному пространству

,
то его можно представить
в базе e
в виде:

=(,,…,)·=·. (1)

Для
вычисления координат вектора-образа:

воспользуемся
определением и свойствами линейного
преобразования
:

====· (2)

5⁰.
Выражение (2) является обобщением
(доказанным!) требования:
=,
где
,
используемое в требовании, всего
лишь число.
Теперь мы видим, что перестановочны
также символы

и
—
строка
координат вектора

в базе
:

=·,
где вектор

есть матрица-столбец.

Так
как
,
— векторы пространства
,
то каждый из них можно записать
координатами в базе
:

==·=·.
(3)

Учитывая
все полученные выражения, можно записать
результат применения линейного
преобразования

к вектору
:

=
=·=··
→
=·. (4)

Замечание:
рассмотрен вариант решения задачи для
случая, когда система векторов базыизображается в виде матрицы-столбца.
Аналогично задача решается для базы,
изображаемой в виде матрицы-строки.

Говорят,
что матрица

задает
линейное преобразование!
В таком случае в векторном пространстве

установлено взаимно
однозначное
соответствие между всеми квадратными
матрицами порядка

и линейными преобразованиями пространства!
Выражение матрицы конкретного линейного
преобразования

зависит от выбора базы, в которой
записывается матрица преобразования.
Это следует из доказательства выражения
(3). Далее эта зависимость будет определена.

Полезно
рассмотреть простые примеры, иллюстрирующие
применение линейного преобразования
векторного пространства
.

☺☺

Пример
10–01:Пусть на плоскости
задана система координат
и определено линейное пространство
геометрических векторов.
При неподвижной системе координат
плоскость поворачивается относительно
точкиOна угол
.
Является ли этот поворот линейным
преобразованием в пространстве?

Решение:

1). Учитывая, что
геометрические векторы свободные, будем
считать, что вектор
имеет начало в точкеO.
Преобразование
переводит вектор в вектор,
принадлежащий.

2). Пусть заданы
два произвольных вектора
и,
принадлежащие.
В соответствии с определением операций
суммы геометрических векторов и умножения
вектора на число построим вектор:
=+и вектор
=·.

3). Вектор диагональ
параллелограмма, построенного на
векторах
и.
Преобразование
есть поворот диагонали параллелограмма
на уголотносительно точкиO.Преобразование, применённое к векторам
и
,
поворачивает каждый из них на тот же
угол
.
В таком случае требование
=+выполняется.

4). Геометрически
очевидно также, результат не зависит
от того, что будет меняться порядок
операций: сначала вектор
умножить на число,
потом повернуть получившийся вектор
на угол
,
или наоборот. В
таком случае требование=
выполняется.

5). Заданное
преобразование плоскости является
линейным преобразованием пространства
.

Ответ:
является.

Пример
10–02:
Показать, что умножение квадратных
матриц 2-го порядка слева на данную
матрицуявляется линейным преобразованием
пространства всех матриц 2-го порядка.

Решение:

1). Запишем
произвольный вектор пространства:
==
x₁+x₂+x₃+x₄,
и определим преобразование
:
то есть произведение:=·.

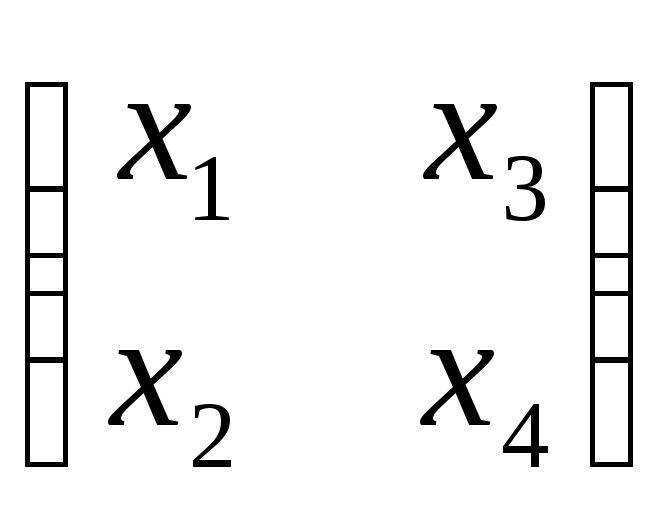
2). Используя
линейные свойства матриц, запишем:
=·,
и=·.
Это значит, что требование линейного
преобразования: =
выполняется.

3). Пусть задан
также вектор: =,
и записано:=·.

4). Запишем сумму
векторов:
==+и линейное преобразование суммы векторов:=·.
Учитывая линейные свойства матриц,
получаем: требование линейного
преобразования:=также выполняется.

5). Вывод:
заданное преобразование
— линейное.

Ответ:
является линейным преобразованием.

Пример
10–03:
Пусть задан вектор=(x₁,x₂,x₃)
линейного пространства.
Записано преобразование пространства:=(x₂+x₃,2x₁+x₃,3x₁–x₂+x₃).
Выяснить, является ли оно линейным. Если
преобразование линейное, найти его
матрицу в том же базисе, в котором заданы
векторыи.

Решение:

1). Запишем базис
пространства:
=(1,0,0),
=(0,1,0),=(0,0,1).
Это значит, что произвольный вектор
линейного пространства может быть
записан в виде:=x₁+x₂+x₃.

2). Пусть заданы
два произвольных вектора

и ,
принадлежащие .
В соответствии с определением операций
суммы векторов:=+=(x₁+y₁,x₂+y₂,x₃+y₃)
и=(x₁,x₂,x₃).

3). Запишем
векторы-образы для векторов, участвующих
в доказательстве линейности
:

=
(+y₃,
2+y₃,
3y₁–+y₃)
и
=(x₂+x₃,2x₁+x₃,3x₁–x₂+x₃);

==
(+x₃++y₃,
2+x₃+2+y₃,
3x₁–++3y₁–+y₃).

4). Из представленных
записей следует: требование
=выполняется,
требование=
выполняется → преобразование
— линейное.

5). Матрицу линейного
преобразования легко получаем (видим!),
если изобразить шаблон выражения
=·:

=
(x₂+x₃,2x₁+x₃,3x₁–x₂+x₃)=
(x₁,x₂,x₃)
·.

Ответ:
является линейным преобразованием
с матрицей:.

Пример
10–04:
Пусть задан вектор=(x₁,x₂,x₃)
линейного пространства.
Записано преобразование пространства:=(x₁–x₂+x₃,
x₃,
x₂).
Выяснить, является ли оно линейным. Если
преобразование линейное, найти его
матрицу в том же базисе, в котором заданы
векторыи.

Решение:

1). Запишем базис
пространства:
=(1,0,0),
=(0,1,0),=(0,0,1).
Это значит, что произвольный вектор
линейного пространства может быть
записан в виде:=x₁+x₂+x₃.

2). Пусть заданы
два произвольных вектора

и ,
принадлежащие .
В соответствии с определением операций
суммы векторов:=+=(x₁+y₁,x₂+y₂,x₃+y₃)
и=(x₁,x₂,x₃).

3). Запишем
векторы-образы для векторов, участвующих
в доказательстве линейности
:

=
(y₁–y₂+y₃,
y₃,
y₂)
и =((x₁–x₂+x₃),
x₃,
x₂);

==
(+y₁–(+y₂)++y₃,
+y₃,
+y₂).

4). Из представленных
записей следует: требование
=
выполняется, требование=
выполняется → преобразование
— линейное.

5). Матрицу линейного
преобразования легко получаем (видим!),
если изобразить шаблон выражения
=·:

=
(x₁–x₂+x₃,
x₃,
x₂)=
(x₁,x₂,x₃)
·.

Ответ:
является линейным преобразованием
с матрицей:.

Пример
10–05:
Показать, что дифференцирование является
линейным преобразованием пространства
всех многочленом степени от одного
неизвестного с вещественными
коэффициентами. Найти матрицу этого
преобразования в базе:

а) 1, x;x²; … ,
;

б) 1, x—c;
;
… ,
гдеc
— вещественное число.

Решение:

Общая
часть для обоих заданий:

1). Запишем
в базе а)многочлен:=,
его координаты – коэффициенты при
переменной. Аналогично=.Сумма многочленов:k=+=;
произведение многочлена на вещественное
число:=
.

2). Обозначим:
-оператор дифференцирования.
Используя теоремы математического
анализа, замечаем, что оператор
является линейным по отношению к
векторам-многочленам, записанным в базе
а).

3). Пусть многочлен
записан в виде:
=,
его координаты в базе б) – вещественные
числа. Вопрос о линейностине вызывает затруднений.

Задание
а):
используем
базу а).

4). Запишем производную
для многочлена:
=по независимой переменнойx,
используя правила дифференцирования:

==
,

координаты в базе
а) вектора
:m‘=(,,
…,
,
0).

5). Матрицу линейного
преобразования легко получаем (видим!),
если изобразить шаблон выражения
=·:

=(,,
…,
,
0)= ()
·.

Задание
б):
используем
базу б).

6). Запишем производную
для многочлена:
=по независимой переменнойx,
используя правила дифференцирования:

==
,

координаты в базе
а) вектора
:m‘=(,,
…,
,
0).

7). Матрицу линейного
преобразования легко получаем (видим!),
если изобразить шаблон выражения
=·:

=(,,
…,
,
0)= ()
·.

Ответ:— линейное преобразование как для
базы, заданной в записи а), так и в записи
б) с матрицей: для случая а):C₁.
для случая б):C₂.

Пример
10–06:
Пусть совокупность векторов:e=(,,)
есть база трехмерного линейного
пространства. В этой базе задан вектор

=(5+–2)=(5,1,-2).
Пустьлинейное
преобразование
задается
матрицей:=в базе
,
которая используется в виде матрицы-столбца.
Найти образ
.

Решение:

1). Воспользуемся
формулой (4) для вектора
:
==·.

2). В нашем случае
получаем:
=
(5,1,–2) ·=(–9,
4, –6).

Ответ:
=(–9,
4, –6).

☻

Соседние файлы в папке ЛА и АГ пособие

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Матрица перехода

Пусть и — два различных базиса линейного пространства .

Матрица , столбцы которой равны координатам векторов в базисе называется матрицей перехода от базиса к базису Тогда

Определитель матрицы перехода отличен от нуля:

Пример с решением

Пример 183.

Определим матрицу перехода от базиса к базису

Запишем координаты векторов в виде строк матрицы и приведем полученную матрицу к ступенчатому виду.

Справа от матрицы указываются векторы и регистрируются проводимые преобразования матрицы.

Нулевым строкам ступенчатого вида матрицы соответствуют равенства Отсюда и

Получено разложение векторов и по базису . Записав коэффициенты этого разложения в виде столбцов матрицы, получим матрицу перехода . Тогда

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Мы ограничимся далее изложением простейших фактов для однородных цепей Маркова, в которых условная вероятность появления события в -м испытании при условии, что в -м испытании осуществилось событие не зависит от номера испытания. Мы назовем эту вероятность вероятностью перехода и обозначим буквой ; в этом обозначении первый индекс всегда будет обозначать результат предшествующего испытания, а второй индекс указывает, в какое состояние перейдет система в последующий момент времени.

Полная вероятностная картина возможных изменений, осуществляющихся при переходе от одного испытания непосредственно к следующему, задается матрицей

составленной из вероятностей перехода, которую мы будем называть матрицей перехода.

Отметим, каким условиям должны удовлетворять элементы этой матрицы. Прежде всего, они, как вероятности, должны быть неотрицательными числами, т.е. при всех и

Далее из того, что при переходе из состояний в -м испытании

система обязательно переходит в одно и только в одно из состояний в -м испытании, вытекает равенство

Таким образом, сумма элементов в каждой строке матрицы перехода равна единице.

Возможно вам будут полезны данные страницы:

Наша первая задача в теории цепей Маркова состоит в определении вероятности перехода из состояния в -м испытании в состояние через испытаний. Обозначим эту вероятность знаком

Рассмотрим какое-нибудь промежуточное испытание с номером . В этом испытании осуществится какое-то одно из возможных событий . Вероятность такого перехода, согласно с только что введенными обозначениями, равна . Вероятность же перехода из состояния в состояние равна . По формуле полной вероятности

Обозначим через матрицу перехода через п испытаний

Согласно (1) между матрицами с различными индексами существует соотношение

В частности, при находим, что

при

и вообще при любом

Отметим частный случай формулы (1): при

Преобразование координат. Матрица перехода.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Пусть $L_n -$ произвольное мерное пространство, $B=(e_1, . e_n) -$ фиксированный базис в нем. Тогда всякому вектору $xin L_n$ взаимно однозначно соответствует столбец его координат в этом базисе.

$$x=x_1e_1+. +x_ne_nLeftrightarrow X=beginx_1\ vdots\x_nend$$

При этом линейные комбинации над векторами в координатной форме выглядят следующим образом:

$y=lambda xLeftrightarrow Y=lambda X.$

Пусть $B=(e_1, e_2, . e_n)$ и $B’=(e_1′, e_2′, . e_n’) -$ два различных базиса в $L_n.$ Каждый из векторов базиса $B’$ разложим по базису $B:$

Матрицей перехода $T_$ от базиса $B$ к базису $B’$ называется матрица

$T_=begint_&. &t_\. &. &. \t_&. &t_end$ $k$-й столбец которой есть столбец $E’_k$ координат вектора $e’_k$ в базисе $B.$ Если $x -$ произвольный вектор из $L_n,$ $X$ и $X’ -$ столбцы его координат в базисах $B$ и $B’$ соответственно то имеет место равенство $$X’=(T_)^X$$ (формула преобразования координат при преобразовании базиса).

Примеры.

4.15. В постранстве $V_3$ заданы векторы $e_1’=i+j, $ $e_2’=i-j, $ $e_3’=-i+2j-k.$ Доказать, что система $B’=(e_1′, e_2′, e_3′)$ базис в $R_3 $ и написать матрицу перехода $T_$ где $B=(e_1=i, e_2=j, e_3=k).$ Найти координаты вектора $x=i-2j+2k$ в базисе $B’.$

Решение.

Для того, чтобы показать, что система векторов $B’=(e_1′, e_2′, e_3′)$ базис в $R_3, $ достаточно показать, что эти вектора не компланарны.

Из условия мы имеем $e_1’=i+j=(1, 1, 0),$ $e_2’=i-j=(1, -1, 0),$ $e_3’=-i+2j-k=(-1, 2, -1).$ Вектора $e_1′, e_2′, e_3’$ не компланарны, если $begin1&1&0\1&-1&0\-1&2&-1endneq 0.$ Проверим это:

Далее запишем матрицу перехода $T_$

Подставляя этот результат в формулу $X’=(T_)^X,$ получаем:

4.17. Пусть $B=(i, j, k)$ и $B’=(i’, j’, k’) -$ прямоугольные базисы в $R_3.$ Написать матрицу перехода $T_,$ и выписать столбец координат вектора $x=i-2j+k$ в базисе $B’.$

Базис $B’$ получен перестановкой $i’=j,$ $j’=k,$ $k’=i.$

Решение.

Из условия мы имеем $e_1=i, e_2-j, e_3=k;$ $e_1’=j=(0, 1, 0),$ $e_2’=k=(0, 0, 1),$ $e_3’=i=(1, 0, 0).$

Подставляя этот результат в формулу $X’=(T_)^X,$ получаем:

Домашнее задание.

Пусть $B=(i, j, k)$ и $B’=(i’, j’, k’) -$ прямоугольные базисы в $R_3.$ Написать матрицу перехода $T_,$ и выписать столбец координат вектора $x=i-2j+k$ в базисе $B’.$

4.16. Базис $B’$ получен изменением на противоположное направление всех трех базисных ортов $B.$

4.18. Базис $B’$ получен поворотом базиса $B$ на угол $varphi$ вокруг орта $i.$

Геометрия данных 5. Преобразование базиса

Под преобразованием базиса системы координат понимается замена одного набора базовых вершин (реперов) на другой. По сравнению с обычной системой координат на векторах изменение системы координат на точечном базисе имеет особенности, связанные с тем, что базисы могут принадлежать разным пространствам.

Основные матрицы

Под матрицами преобразования (матрицами перехода) обычно понимают такие матрицы, при умножении на которые координат элемента (вершины) в старом базисе, получаются ее координаты в новом. На основании данных матриц преобразуются также метрические тензоры из одного базиса в другой.

Матрицы преобразования базисов содержат сравнительные характеристики двух базисов. Среди данных матриц выделятся инвариантные матрицы — их значения не зависят от выбора базиса. Например, матрица дистанций между вершинами является инвариантной.

Прямые матрицы перехода

Набор исходных базовых вершин обозначим как (старый базис), новый набор как (новый базис). Для преобразования координат должна быть задана матрица перехода — описание координат вершин нового базиса в старом. Такими координатами могут быть как ди-координаты вершин, так и би-координаты. Матрицу перехода в ди-координатах обозначим как . Строка матрицы — это координаты вершины нового базиса в старом , соответственно столбец — это ди-координаты вершины старого базиса относительно нового.

Матрица перехода должна быть квадратной, следовательно одних координат вершин недостаточно — их количество меньше, чем количество компонент координат (из-за наличия скалярной компоненты в координатах). Поэтому необходимо добавить в данную матрицу ди-координаты вектора нормали [0; 1, 1,… 1]. После чего матрица перехода в ди-координатах становится похожей по форме на мажорный грамиан. Назовем матрицу дистанционным тензором преобразования координат (ДТП):

Дистанционный тензор преобразования является инвариантом — его значения не зависят от базиса. При обратном переходе (от к ) значения даной матрицы просто транспонируются (строки и столбцы меняются местами).

Поскольку ДТП — это ди-координаты, то умножая их на лапласиан (ЛМТ), можно получить би-координаты . Структура би-координат матрицы перехода:

Первая строка данной матрицы — это би-координаты нормали: .
В отличие от ДТП значения би-координат матрицы перехода зависят от того, для какого базиса они получены — для старого или нового. Выбор базиса определяет матрицу ЛМТ. Для определенности би-координаты перехода в базисе обозначим как , а в базисе как . Тогда имеют место следующие тождества. Для исходного базиса:

Здесь и — лапласиан и грамиан исходного базиса. Соответственно и — метрические тензоры нового базиса.

При переходе от одного базиса к другому требуется определить метрические тензоры нового базиса, если заданы матрицы преобразования.

Обратные матрицы перехода

Матрицы перехода и обратимы при условии отличного от нуля детерминанта матрицы перехода:

Нулевой детерминант матрицы преобразования означает ортогональность базисов. В ортогональном базисе невозможно выразить метрику проекций. Будем считать базисы неортогональными. Тогда обратные матрицы перехода выражаются через прямые следующим образом:

Матрица — представляет собой би-координаты вершин старого базиса относительно вершин нового . То есть обращение би-координат дает взаимные би-координаты.

Матрица — это лапласовский тензор преобразования базиса (ЛТП). Ее структура аналогична структуре лапласиана (ЛМТ):

Здесь главный минор — это симметричный лапласиан. В окаймлении барицентрические координаты обратных проекций ортоцентров двух базисов (симплексов). Ортоцентр исходного базиса выражена в барицентрических координатах нового — , а ортоцентр нового в координатах исходного — .
Что понимается под «обратными проекциями», будет пояснено далее.

В углу лапласовского тензора находится скаляр . Его значение отражает скалярное произведение двух базисов — нового и старого. Чтобы раскрыть его смысл, рассмотрим две ситуации — 1) базисы принадлежат одному и тому же пространству и 2) базисы принадлежат разным пространствам.

Скалярное произведение базисов одного пространства

В общем пространстве скалярное произведение базисов выражается через нормы ортоцентров ( и ) и расстояния между ортоцентрами ():

Данная формула подобна выражению для скалярного произведения пар с общей вершиной (3.8). Поэтому можно считать соотношение (5.5) определением скалярного произведения ортоцентров.

На рисунке показана геометрическая интерпретация скалярного произведения ортоцентров (окружностей). Слева — определение через скалярное произведение смежных пар и . Если окружности пересекаются, то у них есть общий элемент — элемент смежности пар.

Скалярное произведение элементов можно определить через их взаимные степени (показано на рисунке справа). Геометрическое определение степени точки дано во 2-й части. Согласно (2.9) степень точки относительно элемента выражается через дистанцию от точки до элемента и норму элемента :

Можно обобщить данное определение, если вместо точки использовать другой элемент. Тогда взаимной степенью двух элементов и является следующая скалярная величина :

Данная формула известна как произведение Дарбу. На правом рисунке показано построение точек, значение дистанции между которыми равно взаимной степени элементов:

По своим свойствам взаимная степень элементов обобщает свойства степени точки, то есть определяет их взаимное расположение. Если элементы находятся вне друг друга, то их взаимная степень положительна, если пересекаются — отрицательна. Под пересечением здесь понимается ситуация, при которой точки касания (или ) находятся внутри элемента (или соответственно) (на рисунке взаимная степень элементов положительна).

Тогда скалярное произведение (5.5) — это взаимная полустепень элементов (и наоборот). Напомним (2.10), что под полустепенью понимается степень, деленная на (-2):

Если центры элементов совпадают (), то их скалярное произведение будет равно их средней норме:

Скалярное произведение базисов разных пространств

Если базисы принадлежат разным пространствам, то геометрическая интерпретация их скалярного произведения усложняется. Приведем вначале алгебраические тождества. Они аналогичны подобным для составляющих лапласовского тензора, приведенных в первой части.

Скалярное произведение базисов может выражено через отношение детерминантов дистанционной матрицы перехода и ее главного минора (см. 5.1.1):

Связь взаимной нормы базисов и барицентрических координат обратных проекций их ортоцентров:

— для вершин базиса .

— для вершин базиса .

Разберемся, что такое обратная проекция точки. Допустим, что у нас есть точка , принадлежащая базису . Тогда ее обратной проекцией на базис будет такая точка , что перпендикуляр, опущенный из нее на базис , пересекается с ним в исходной точке .

На рисунке обратной проекцией точки на пространство является точка , а обратной проекцией точки на пространство — точка . Точки и — это ортоцентры базисов и соответственно.

Понятие обратной проекции применимо также к нормам элементов. Норма при обратной проекции становится больше исходной (в отличие от прямой проекции). На рисунке дистанция — это норма ортоцентра базиса . Обратной проекцией на базис будет дистанция:
.
Соответственно обратной проекцией нормы базиса на базис будет дистанция
.
Обозначая дистанцию между обратными проекциями центров как , получаем следующее выражение для скалярного произведения базисов разных пространств:

Видим, что по форме оно совпадает со взаимной нормой базисов одного пространства (5.5), но вместо дистанций используются их обратные проекции на взаимный базис. Если базисы принадлежат одному пространству, то угол между пространствами становится нулевым, и формула (5.9) переходит в (5.5).

Все приведенные формулы применимы также и к пространству графа. В графе нет описанных сфер (базиса), но есть связность. Тогда скалярное произведение базисов графа должно отражать их взаимную связность.

Расчет нового базиса

Здесь также рассмотрим две ситуации: 1) новый и старый базис принадлежат одному и тому же пространству и 2) принадлежат разным пространствам. Первый случай как правило относится к обычному геометрическому пространству (при смене базиса тут редко меняется его пространство), второй — к пространству графа.

Определить принадлежность элемента (вершины) пространству базиса можно по его норме в данном пространстве. Если равна нулю, то элемент принадлежит пространству.

Единое пространство базисов

Для получения грамиана нового базиса необходимо умножить ди-координаты элементов нового базиса на би-координаты . Полученная матрица будет матрицей скалярных произведений в новом базисе (см. 4.4.2 в предыдущей части). Таким образом если пространства базисов совпадают, то матрица норм вершин нового базиса относительно старого — это и есть грамиан нового базиса:

Мы пометили данный грамиан штрихом, чтобы помнить об условии общего пространства базисов. Лапласиан нового базиса (ЛМТ) можно получить обращением грамиана (ДМТ):

Координаты элемента в новом базисе могут быть выражены через координаты в старом и матрицы перехода. Ди-координаты :

Би-координаты элемента в новом базисе :

Все приведенные выражения аналогичны формулам изменения координат и в обычных (векторных) системах координат. В пределах общего пространства использование точечного базиса аналогично использованию векторного.

На КДПВ показан основной базис из 3-х вершин (A, B, C) и новый базис , образованный вершинами (P, Q, R). Значения ДМТ основного базиса есть в первой статье:
begin
Gm_ & * & A & B & C \
hline
* & 0 & 1 & 1 & 1 \
A & 1 & 0 & -4.5 & -8 \
B & 1 & -4.5 & 0 & -12.5 \
C & 1 & -8 & -12.5 & 0 \
end
Звездочкой обозначена скалярная компонента. Значение лапласиана (ЛМТ) можно получить обращением грамиана (ДМТ).

Дистанционную матрицу перехода считаем заданной. Ее вид:
begin
Dm_ & * & A & B & C \
hline
* & 0 & 1 & 1 & 1 \
P & 1 & -1.0 & -2.5 & -13.0 \
Q & 1 & -6.5 & -2.0 & -6.5 \
R & 1 & -12.5 & -2.0 & -20.5 \
end

Значения би-координат матрицы перехода получаем по формуле (5.2.1):
begin
Ba_p^a & * & A & B & C \
hline
* & 1 & 0 & 0 & 0 \
P & -1.5 & 0.91(6) & 0.(3) & -0.25 \
Q & 2.0 & -0.5 & 1.0 & 0.50 \
R & -5.0 & -0.(6) & 1.(6) & 0.0 \
end
Скалярной компонентой (значения первого столбца) би-координат являются орбитали. Сумма барицентрических компонент равна 1.

Лапласовский тензор преобразования (5.3.1):
begin
Lt^ & * & P & Q & R \
hline
* & 2.15 & 0.30 & 1.15 & -0.45 \
A & 0.058(3) & 0.11(6) & -0.0(6) & -0.05 \
B & 0.9(6) & -0.0(6) & -0.0(3) & 0.10 \
C & -0.025 & -0.05 & 0.10 & -0.05 \
end
Вектор — это барицентрические координаты ортоцентра старого базиса (симплекса ABC) относительно вершин нового (PQR). Соответственно, вектор — наоборот, барицентрические координаты ортоцентра симплекса PQR относительно вершин старого базиса.

Базисы в разных пространствах

Если базисы находятся в разных пространствах, то формула (5.10.1) будет давать неверные значения полудистанций между вершинами нового базиса. В предыдущей части было показано, что в общем случае для нахождения правильных дистанций между вершинами необходимо к матрице норм прибавить фундаментальную матрицу (4.5):

Следовательно, при преобразовании базиса к базису из другого пространства необходимо наряду с матрицами перехода задать фундаментальную матрицу нового базиса (относительно исходного).

Для задания фундаментальной матрицы полезно вспомнить ее геометрический смысл (см. 4.6.1). Элемент фундаментальной матрицы — это скалярное произведение нормалей, направленных к вершинам из их проекций на пространство базиса. В частном (но практически важном) случае общего надпространства элемент фундаментальной матрицы вычисляется как произведение расстояний от заданных элементов до пространства базиса.

Скалярное произведение обратных проекций

В пространстве графа значения фундаментальной матрицы можно получить через матрицу смежности между старым и новым базисом . Элементами данной матрицы является вес связей между вершинами двух базисов. Если матрица известна и обратима, то можно получить обратную матрицу смежности:

Полученная матрица (как и матрица смежности) является инвариантом — ее значения не зависят от выбора базиса. Значения элементов матрицы отражают скалярное произведение обратных проекций между вершинами двух базисов. На рисунке представлена поясняющая схема.

Здесь точка A принадлежит базису , а точка P — базису . Штрихами помечены обратные проекции точек на смежный базис. Тогда значение элемента матрицы — это скалярное произведение векторов и :

Можно выразить данное соотношение через расстояния от вершин до гиперплоскости пересечения пространств (на рисунке — точка O) и угол между пространствами :

Из формулы (5.13.2′) видно, что если базисы ортогональны , то элементы скалярного произведения обращаются в бесконечность.

Итоговые формулы преобразования базисов

Удобно привести размерность матрицы скалярных произведений проекций к размерности остальных матриц перехода, окаймив ее нулями. Тогда фундаментальная матрица базиса определяется как

Объединяя все вместе, получаем конечное выражение для грамиана нового базиса :

Симметричным образом выражается исходный базис при заданных матрицах преобразования:

Здесь и — би-координаты матриц перехода (5.2.1) и (5.2.2). — общая дистанционная матрица преобразования:

Данная матрица является инвариантом, состоит из двух частей — дистанционного тензора преобразования и добавки, связанной с некомпланарностью пространств базисов, — матрицы скалярных произведений проекций .

Лапласовский тензор базисов получается обращением ДМТ (5.15). Задача определения связи базисов решена.

Подводим итоги. Тяжелая формульная часть серии в целом завершена. Приведены основные понятия и тождества. Точечные базисы — это полезный и мощный инструмент для различных прикладных задач. В заключительной статье рассмотрим базис простейшей структуры — в виде звезды.

Содержание:

1. Линейные преобразования. Собственные векторы и собственные числа линейного оператора
2. Собственные векторы и собственные числа линейного оператора: определение, свойства
3. Нахождение собственных чисел и собственных векторов
4. Базис пространства из собственных векторов линейного оператора
5. Линейная модель обмена (модель международной торговли)

Линейные преобразования. Собственные векторы и собственные числа линейного оператора

Линейные преобразования (линейные операторы). Матрица линейного преобразования

Пусть задано -мерный пространство . Если каждому вектору поставлено в соответствие единственный вектор

этого же пространства, говорится, что в векторном пространстве  задано преобразование , или оператор .

Вектор — результат линейного преобразования — называют образом вектора , а выходной вектор  — прообразом вектора .

Преобразование называется линейным преобразованием, или линейным оператором, если для произвольных векторов и произвольного действительного скаляра выполняются условия:

То есть линейный оператор преобразует пространство  в то самое пространство. Это записывается следующим образом:

Примерами простейших линейных преобразований являются:
тождественное преобразование: , когда каждый -мерный вектор пространства превращается в самого себя, то есть остается без изменения;

нулевой оператор , когда каждый -мерный вектор пространства превращается в ноль-вектор этого же пространства, то есть

Линейное преобразование , с помощью которого осуществляется восстановление вектора  по его образу , называется обратным к линейным преобразованием. В отличие от матрицы оператор записывают каллиграфическим шрифтом.

Рассмотрим задачу об отыскании координат образа вектора .

Пусть в пространстве  выбрано базис (не обязательно ортонормированный) и есть координатами вектора в этом базисе. Обозначим через координаты вектора в выбранном базисе. по условию , тогда согласно линейностью оператора  получим :

Но образы тоже являются векторами с , поэтому иx можно разложить по тому же базисом. Пусть

где  коэффициенты разложения вектора  по базису  

С учетом (5.5) соотношение (5.4) принимает вид:

Группируя члены правой части относительно векторов базиса, имеем:

С другой стороны, если  являются координатами вектора  в базисе  то его можно представить следующим образом:

Сопоставляем (5.8) из (5.7) и получаем координаты вектора :

Следовательно, при линейном преобразовании:

координаты образа вектора являются линейными комбинациями координат прообраза, коэффициенты при которых составляют матрицу -го порядка (обозначим ее через ):

Матрица , которая в произведении (слева) с вектором с  определяет координаты его образа при линейном преобразовании , Называется матрицей линейного преобразования  в базисе  и пишут:

Каждый — -й — столбец матрицы составляют коэффициенты разложения вектора  по базису каждая — -я — строка определяет коэффициенты разложения координат вектора по координатам вектора .

Обратите внимание, что — нераздельный символ (обозначение вектораобраза), а — произведение матрицы с вектором (прообразом).

Каждому линейном оператору -мерного пространства отвечает матрица -го порядка в данном базисе. И наоборот, каждой матрицы -го порядка отвечает линейный оператор -мерного пространства с определенным базисом.

Например, с помощью оператора линейных преобразований можно описать поворот произвольного вектора с пространства вокруг начала координат на угол  против часовой стрелки. Формулы поворота осей координат (формулы перехода от исходных координат и к новым  и , и наоборот ) определяют алгебраическую форму изображения линейного оператора поворота осей:

где  оператор перехода от исходных (новых) координат к новым (исходных);

 векторы, началом которых является точка , а концами —
точки и , соответственно.

По соотношению (5.12) матрица линейного преобразования} , Описывающий поворот произвольного вектора из пространства вокруг начала координат на угол против часовой стрелки, имеет вид:

а матрица обратного линейного преобразования , то есть такого, что описывает поворот произвольного вектора из пространства вокруг начала координат на угол  по часовой стрелке, имеет вид:

Теорема 5.1 (о связи между матрицами оператора в различных базисах).

Матрицы и  линейного оператора в разных базисах и связаны между собой соотношением:

где  матрица перехода от исходного к новому базису.

Доказательство. Пусть линейный оператор превращает вектор пространства  в вектор того самого пространства. Тогда в матричной форме связь между вектором и его образом в исходном базисе можно записать как , а в новом — как . Поскольку является матрицей перехода от исходного базиса к новому, то в соответствии с (4.18) имеем:

Умножим равенство (5.14) слева на матрицу и получим . Отсюда по определению линейного оператора имеем: . С учетом (5.15):

Сравнив соотношение  и , получаем 

Две квадратные матрицы и называются подобными, если существует такая невырожденная матрица , матрицы и связанные соотношениями:

Соответствующие линейные операторы называются преобразованиями сходства.

Подобные матрицы описывают то же линейное преобразование, но в разных базисах, а матрица является матрицей перехода от одного базиса к другому.

Подобные матрицы имеют те же ранги, суммы элементов главной диагонали и определители.

В базисе и задана матрица линейного оператора :

Определим матрицу , которая отвечает том же оператору в базисе векторов  и  есть матрица  подобна матрице .

Предоставим расписание векторов нового базиса по векторам исходного базиса: . Соответственно, матрица перехода от исходного к новому базису имеет вид:

Ее определитель , то есть матрица невырожденная и имеет обратную: 

По теореме 5.1 определяем матрицу оператора в новом базисе:

Обратите внимание, что в новом базисе матрица оператора оказалась диагональной.

Собственные векторы и собственные числа линейного оператора: определение, свойства

Рассмотрим -мерных линейный пространство  с определенным базисом и матрицу , некоторого линейного оператора пространства.

Ненулевой вектор называют собственным, или характеристическим вектором линейного оператора (или матрицы ), если существует такое действительное число , имеет место равенство:

Скаляр называется собственным, или характеристическим, числом матрицы , или ее собственным значением, соответствует собственному вектору :

Согласно определениями собственного числа и собственного вектора имеем:

1) Если , то каждый ненулевой вектор из  является собственным вектором матрицы , при этом , ведь по свойству единичной матрицы имеем ;
2) любой ненулевой -мерный вектор является собственным вектором нулевой матрицы , при этом , так как .

Поставим задачу нахождения собственных чисел и собственных векторов заданной матрицы 

Поставим задачу нахождения собственных чисел и собственных векторов заданной матрицы

Запишем матричное уравнение (5.17) в развернутом виде:

Таким образом, задача сводится к решению однородной системы линейных уравнений с  неизвестными. Нас интересуют (по определению собственного вектора) только ненулевые векторы, то есть нетривиальные решения системы, поэтому определитель системы (5.18) должен быть равен нулю:

Раскрытие определителя в соотношении (5.19) дает многочлен степени относительно , который называется характеристическим многочленом матрицы , а соотношение (5.19), которое можно представить в виде , определяет уравнение для нахождения собственных чисел, которое называют характеристическим уравнением матрицы .

По основной теореме алгебры уравнения любой матрицы  имеет корней, если каждый из них считать столько раз, какова его кратность. Характеристическое уравнение матрицы может иметь только действительные, но и комплексные корни, то есть числа вида где действительные числа, мнимая единица.

Множество всех собственных чисел матрицы называют спектром матрицы. Если в спектре матрицы то же собственное число повторяется раз, то говорят, что кратность этого собственного числа равна .

Теорема 5.2 (о единственности собственного чucлa, что соответствует собственному вектору). Если — собственный вектор матрицы , то существует единственный скаляр , который удовлетворяет условие .

Доказательство. Предположим, что кроме собственного числа существует еще один
скаляр , такой, что . Тогда должно выполняться равенство . Поскольку по определению собственный вектор является ненулевым, то есть , получим .

Согласно теореме 5.2 говорят, что собственный вектор  из матрицы принадлежит собственному числу . 

Теорема 5.3 (о множестве собственных векторов, принадлежащих собственному числу). Если матрица имеет собственный вектор, принадлежащий собственному числу , то таких векторов бесконечно много.

Доказательство базируется на определении собственного вектора и свойствах ассоциативности и коммутативности операции умножения матрицы на скаляр.

Действительно, пусть собственный вектор матрицы , тогда . Привлечем к рассмотрению вектор , коллинеарный вектору , то есть ,  где , и покажем, что в также является собственным вектором матрицы :

Поскольку равенство (5.19) выполняется для произвольного , то существует множество собственных векторов, принадлежащих данному собственному числу.

Теорема 5.4 (критерий существования собственного вектора , соответствующего собственному числу ). Вектор тогда и только тогда является собственным вектором матрицы , соответствующим собственному числу , когда его координаты образуют ненулевое решение однородной квадратной системы линейных алгебраических уравнений

 или 

Доказательство сводится к тождественных преобразований матричных уравнений.

Необходимость уже доказано переходом от соотношения , к однородной системе линейных уравнений , представленной в развернутом виде (5 18).

Достаточность. На основании свойств действий над матрицами с учетом условия , осуществит переход от однородной системы уравнений в матричной форме с соотношением :

Теорема 5.5 (пpo линейную независимость собственных векторов). Собственные векторы, принадлежащие различным собственным числам, является линейно независимыми.

Доказательство проведем методом от противного. Пусть два произвольные собственные векторы, принадлежащие соответственно собственным числам и . Необходимо показать, что линейная комбинация этих собственных векторов ноль-вектор только тогда, когда , то есть

Предположим обратное. Пусть (5.23) выполняется при условии, что одно из чисел не является нулем, например,

Умножим левую и правую части (5.23) на собственное число . Тогда

Левую и правую части равенства (5.23) умножим на матрицу слева, и, учитывая свойства операций над матрицами, получим:

Сравним (5.25) и (5.24). Получаем:

По условию теоремы . По определению вектор  является ненулевым, поэтому равенство (5.26) возможно только при , то есть предположение о линейной зависимости векторов и  ошибочно.

Если есть более двух собственных векторов, принадлежащих попарно различным собственным числам, доведение аналогичное (с использованием метода математической индукции).

Заметим, что собственные векторы, принадлежащих различным собственным числам, можно использовать как базисные векторы пространства .

Теорема 5.6 (пpo сумму и произведение собственных чисел). Если собственные числа матрицы , то:
1) сумма собственных чисел равна сумме элементов главной диагонали матрицы :

2) произведение собственных чисел равна определителю матрицы :

Доказательство основывается на формулах Виета, которые описывают соотношение между корнями и коэффициентами многочлена -гo степени в случае, когда его старший коэффициент равен единице.

Рассмотрим простейший случай . Запишем характеристическое уравнение в развернутом виде:

С (5.29) по теореме Виета (для квадратного уравнения) имеем:

Сумму всех диагональных элементов матрицы называют следом (от нем. spur — след) этой матрицы и обозначают .

Для квадратной матрицы произвольного порядка теорему 5.6 в символьном виде можно записать так:

при этом собственное число берем столько раз, какова его кратность как корня характеристического уравнения (5.29).

Нахождение собственных чисел и собственных векторов

Рассмотрим алгоритм нахождения собственных чисел матрицы и собственных векторов, которые им принадлежат.
Согласно соотношениями (5.18) и (5.19) имеем такой порядок отыскания собственных чисел и собственных векторов матрицы.
1. Составляем по исходной матрицей характеристическое уравнение (5.18) и решаем его, то есть находим спектр собственных чисел.
2. Подставляем поочередно каждое собственное число в систему (5.18) и находим все ее нетривиальные решения, что и дает множество собственных векторов, принадлежащих соответствующему собственному числу.

Замечания. Множество всех собственных векторов, принадлежащих определенному собственному числу, можно представить как линейную комбинацию фундаментальных решений однородной системы уравнений согласно (4.19), гл. 4.

Найдем собственные числа и собственные векторы матрицы

Характерным уравнением этой матрицы является квадратное уравнение:

Решив его, получим собственные числа  и 

Теперь описываем множества и всех собственных векторов, принадлежащих найденным собственным числам.

Для этого в матрицу вместо подставим поочередно значения собственных чисел, запишем соответствующую систему однородных линейных уравнений (5.18) и решим ее:

Предоставляя параметру произвольных значений, для данного собственного числа получим совокупность коллинеарных между собой собственных векторов.

Теорема 5.7 (про собственные числа и собственные векторы симметричной матрицы).

Симметричная матрица имеет только действительные собственные числа. Собственные векторы, принадлежащие разным собственным числам, ортогональны и линейно независимы.

Теорема приводим без доказательства.
Проиллюстрируем прав выводов данной теоремы на примере.

Пусть имеем симметричную матрицу

Найдем собственные числа и собственные векторы этой матрицы и докажем ортогональность собственных векторов, соответствующих различным собственным числам.

1. Составим характеристическое уравнение матрицы

2. Найдем корни полученного кубического уравнения относительно . С элементарной алгебры известно, если многочлен со старшим коэффициентом, равным единице, имеет целые корни, то их следует искать среди делителей свободного члена. Перебирая делители числа 36, убеждаемся, что является корнем уравнения (5.30).

Нахождение других двух корней сводится к решению квадратного уравнения:

3. Опишем множества и собственных векторов, принадлежащих найденным собственным числам.

Для этого в матрицу  вместо подставляем поочередно значения собственных чисел, записываем соответствующую систему однородных линейных уравнений (5.17) и решаем ее методом Жордана-Гаусса:

Аналогично находим собственные векторы  и 

Система векторов  и  является линейно независимой, поскольку 

Убеждаемся, что векторы  и  — попарно ортогональны.
Для этого определим их скалярные произведения:

Поскольку скалярные произведения векторов равны нулю, то векторы попарно ортогональны.
Если в выражениях (5.31-5.33) положить , то получим систему векторов:

которая использовалась как базис пространства в примере после теоремы   и . В таком базисе, то есть базисе из собственных векторов, матрица оператора оказалась диагональной, ее ненулевыми элементами являются собственные числа матрицы .

Теорема 5.8 (о преобразовании матрицы к диагональному виду). Матрица линейного оператора в базисе имеет диагональный вид тогда и только тогда, когда все векторы базиса являются собственными векторами матрицы .
Теорему наводим  без доказательств

Заметим, что при нахождении собственных чисел для заданной матрицы самой задачей является решение алгебраического уравнения -й степени, что во многих случаях сделать невозможно без использования приближенных методов. Изучение приближенных методов выходит за пределы программы. Поэтому предлагаем воспользоваться известными программами MatLab, MathCad, Maple и др.

Следующий пример был решен в пакете MatLab, в котором конечный результат вычислений предоставляется без промежуточных выкладок.
Найдем собственные числа и соответствующие им собственные векторы матрицы

Характерным уравнением для нахождения собственных чисел является уравнение

корнями которого будут числа  а соответствующие им собственные векторы имеют вид: 

Собственные числа и собственные векторы матриц имеют широкий спектр использования, в частности, в аналитической геометрии (Раздел 2), в задачах различных отраслей естественных наук и эконометрики.

Базис пространства из собственных векторов линейного оператора

По теореме 5.5 собственные векторы, принадлежащие разным собственным числам, являются линейно независимыми. Возникает вопрос, при каких условиях существует базис линейного пространства , построенный из собственных векторов матрицы.
Лема. Если является собственным числом матрицы , то множество собственных векторов матрицы содержит линейно независимых векторов, где — ранг матрицы .

Доказательство. Согласно теореме 5.4 множество собственных векторов совпадает с множеством всех решений однородной системы линейных уравнений: 

где — собственный вектор матрицы , что соответствует собственному числу . По теореме 4.4 такая система имеет фундаментальную систему решений, количество векторов которой равна , то есть содержит — линейно независимых векторов.

Теорема 5.9 (о существовании базиса из собственных векторов матрицы). Пусть числа образуют множество всех различных собственных чисел матрицы . Если сумма рангов матриц равна , то в пространстве существует базис из собственных векторов матрицы .

Доказательство. Согласно лемме каждое множество собственных векторов, соответствующих уравнению , содержит независимые векторы в количестве . По теореме 5.5 собственные векторы, принадлежащие разным собственным числам, являются линейно независимыми. Тогда для матрицы общее количество линейно независимых собственных векторов составляет:

Поскольку собственные векторы матрицы  в совокупности составляют систему линейно независимых векторов, то они образуют базис пространства .

Теорема 5.10 (о существовании базиса из собственных векторов симметричной матрицы). Если матрица линейного оператора симметрична, то в пространстве существует базис, образованный из собственных векторов матрицы .

Теорему принимаем без доказательств.
Построим ортонормированный базис пространства , состоящий из собственных векторов матрицы

линейного преобразования , и найдем матрицу заданного преобразования в этом базисе.

Согласно теореме 5.9 такой базис существует, поскольку матрица является симметричной матрицей. Составим характеристическое уравнение матрицы :

и решим его: (собственное значение кратности ) и

Для каждого из двух различных собственных чисел матрицы определим фундаментальную систему решений однородной системы уравнений: . При в результате элементарных преобразований основной матрицы системы получаем:

По последним шагом элементарных преобразований матрицы записываем общее решение системы:

Определяем фундаментальную систему решений однородной системы уравнений 

Собственные векторы и являются ортогональными, поскольку их скалярное произведение равно нулю: 

При в результате элементарных преобразований основной матрицы системы получаем:

По последнем шагом элементарных преобразований матрицы записываем общее решение системы:

Возлагаем и получаем фундаментальный решение однородной системы уравнений 

Поскольку и , то все три вектора попарно ортогональны. Объединив полученные фундаментальные системы решений, иметь систему собственных векторов матрицы  . Они образуют ортогональный базис пространства . После нормирования векторы приобретают вид:

Это и есть ортогональный базис пространства , состоящий из собственных векторов матрицы .

По соотношению (5.13) определим матрицу , что соответствует оператору в базисе из собственных векторов. Согласно теореме 5.8 эта матрица будет иметь диагональный вид, а элементами ее главной диагонали будут собственные числа этой матрицы. Заключим с собственными векторами , и матрицу перехода к новому базису и найдем обратную к ней матрицу :

По матричным уравнением (5.13) находим матрицу , что соответствует оператору в базисе из собственных векторов:

Следовательно, мы получили диагональную матрицу третьего порядка, элементами главной диагонали которой есть собственные числа матрицы .

Далее приведен пример применения собственных векторов и собственных чисел в одной из многих задач экономики.

Линейная модель обмена (модель международной торговли)

Практически все страны кроме внутреннего товарообмена осуществляют внешний товарообмен, то есть занимаются внешней торговлей. Торговля считается сбалансированной, или бездефицитной, если для каждой страны прибыль от торговли не меньше объем средств, которые она вкладывает в товарооборот (внутренний и внешний).

Постановка задачи. Несколько стран осуществляют взаимный товарообмен. Известную долю бюджетных средств, тратит каждая страна на закупку товаров у другой страны, учитывая и внутренний товарооборот. Определить, каким должно быть соотношение бюджетов партнеров для того, чтобы обеспечить бездефицитность торговли.  

Построение математической модели. Введем обозначения количественных характеристик, описывающих торговлю между странами, и определим связь между этими характеристиками. Пусть — страны, участвующие в международной торговле. Доли средств, которые тратит страна на закупку товаров в стране , учитывая и внутренний товарооборот , обозначим через . Понятно, что

Матрицу , элементами которой являются числа , называют структурной матрицей торговли:

Эта матрица описывает взаимодействие стран в процессе международной торговли. Соотношение (5.34) означает, что сумма элементов каждого столбца матрицы равна
1. Если объем средств, которые тратит каждая страна на торговлю, обозначить через , соответственно, то прибыль страны от внутренней и внешней торговли составит

Чтобы торговля каждой страны была сбалансированной, по определению должно выполняться условие , и , то есть прибыль от торговли не должна быть меньше расходов. Однако соблюдение этого требования в виде неравенства невозможно для всех стран в совокупности. Действительно, добавим левые и правые части указанных неровностей, изменяя от единицы до :

Группируя в левой части слагаемые, содержащие каждое из , получим:

Учитывая соотношение (5.20), получим:

Отсюда следует, что сбалансированная торговля возможна только в случае знака равенства. Это, полагаем, понятно не только на основании аналитических выкладок, но и с экономической точки зрения (и даже просто с точки зрения здравого смысла): все страны в совокупности не могут получить прибыль. Более того, для одной из стран не может выполняться знак строгого неравенства .

Итак, условием сбалансированной торговли является равенства , и , из которых получим:

Введем в рассмотрение вектор (бюджетных) средств и подадим систему (5.39) в матричной форме:

С (5.40) следует, что при условии сбалансированности торговли между странами вектор средств должен быть собственным вектором структурной матрицы торговли , который принадлежит собственному числу . Таким образом, решение задачи сводится к нахождению этого собственного вектора , компоненты которого устанавливают соотношение между бюджетами стран, участвующих в товарообмене.

Рассмотрим товарообмен между тремя странами. Пусть структурная матрица торговли стран , имеет вид:

Найдем вектор средств, компонентами которого являются доли от общего объема торговли, должна вкладывать каждая из стран во внешней товарооборот для того, чтобы торговля была сбалансированной.

Искомый вектор средств является собственным вектором структурной матрицы, принадлежащий собственному значению . Его компоненты образуют ненулевое решение однородной СЛАУ:

Поскольку система является однородной, то расширенная матрица эквивалентна основной матрицы системы. Осуществим элементарные преобразования основной матрицы этой системы уравнений:

Находим общее решение системы, в котором — базисные переменные, — свободная переменная: 

Отсюда следует, что для сбалансированности торговли необходимо, чтобы средства, которые вкладывает в внешний товарооборот каждая страна, соотносились как