Обозначим через {e1,e2 ,e3} и {u1,u2} канонические базисы пространств R3 и R2 соответственно. Тогда
|
a |
= e |
b1 |
= u1 |
+2u2 |
||||||
|
1 |
1 |
, |
. |
|||||||
|
a2 = e1 +e2 |
= u1 +u |
|||||||||
|
a |
3 |
= e |
+e |
2 |
+e |
3 |
b2 |
2 |
||
|
1 |
Отсюда находим матрицы перехода от канонических базисов
{e1,e2 ,e3} и {u1, u2} к новым базисам {a1,a2 ,a3}, {b1,b2} :
|
1 |
1 |
1 |
1 |
1 |
|||||||||
|
C = (a1 ,a2 |
0 1 |
||||||||||||
|
,a3 ) = |
1 , |
D = |
2 |
. |
|||||||||
|
0 |
0 |
1 |
|||||||||||
|
1 |
|||||||||||||
|
Вычисляем обратную матрицу |
|||||||||||||
|
1 |
−1 |
−1 |
1 |
, |
|||||||||
|
D−1 = − |
−2 |
= |
|||||||||||
|
1 |
2 |
−1 |
|||||||||||
|
и матрицу отображения f в новых базисах: |
|||||||||||||
|
−1 1 |
0 |
1 |
1 |
1 |
|||||||||
|
A′ = D |
−1 |
0 1 |
= |
||||||||||
|
AC = |
0 1 1 |
||||||||||||
|
2 |
−1 0 |
−1 1 |
0 |
0 |
|||||||||
|
1 |
|||||||||||||
|
0 |
−1 −1 |
0 |
−1 −1 |
||||||||||
|
= |
1 1 |
. |
Ответ: A′ = |
1 |
1 |
. |
|||||||
|
0 |
0 |
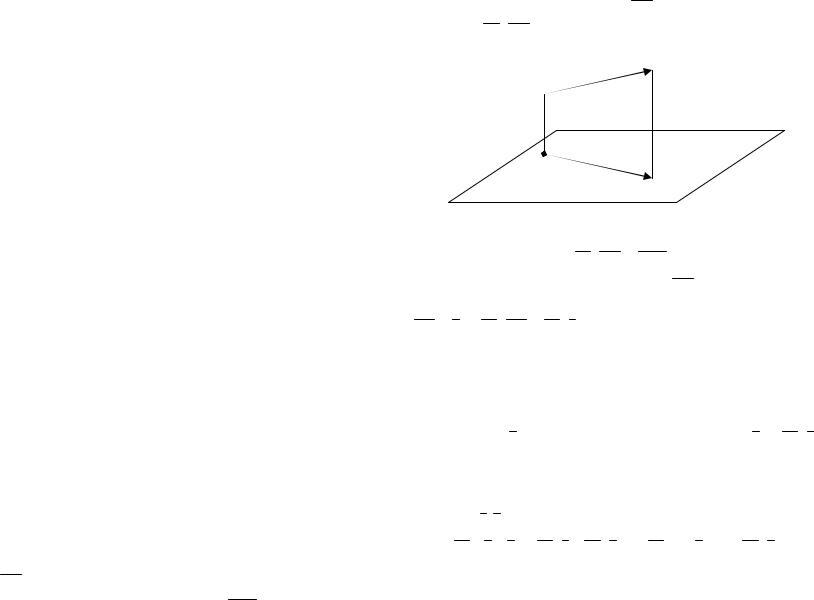
Задача 253. Доказать, что проектирование вектора на плоскость есть линейное отображение.
Решение. Пусть V3 – пространство векторов как на-
правленных отрезков и σ – произвольная плоскость. Введем понятие проекции вектора на плоскость.
Определение. Пусть AB – произвольный вектор и A′, B′ –
проекции на плоскость σ точек А и В. Тогда вектор A′B′ 41
называется проекцией вектора AB на плоскость σ и обо-
значается прσ AB .
В
А
σ
A′
B′
Рис. 1.
Итак, по определению, прσ AB = A′B′. Можно доказать, что
при параллельном переносе вектора AB его проекция на плоскость σ не изменится, поэтому мы можем обозначить
AB = a и прσ AB = прσ a .
Обозначим через Vσ – векторное пространство векто-
ров, как направленных отрезков, лежащих на плоскости σ или параллельных ей, и устроим отображение
f : V3 → Vσ
по правилу: a V3 положим по определению f (a) = прσ a .
Теорема. Отображение проектирования вектора на плоскость является линейным отображением, т.е.
a, b V3 , λR выполняются равенства:
прσ (a + b) = прσ a +прσ b и прσ (λa) = λпрσ a . Доказательство. Теорему можно доказать, используя чисто геометрические средства и методы, но мы докажем
42
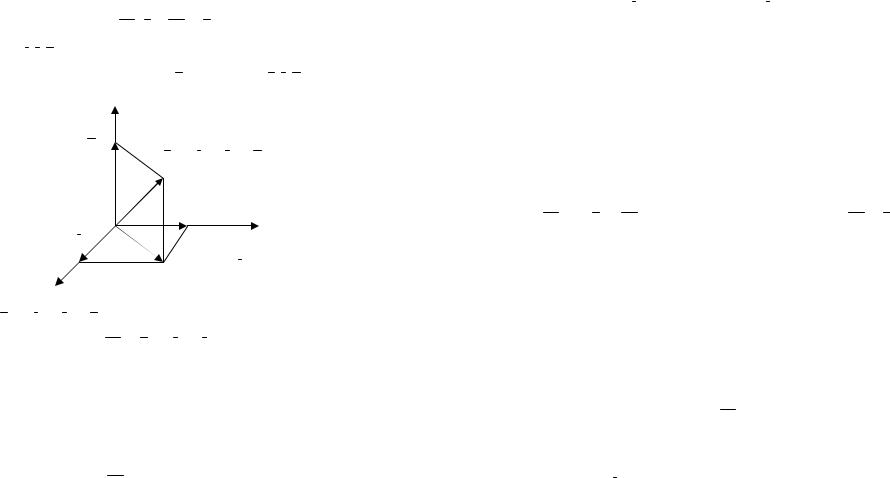
ее с помощью метода координат, опираясь на то, что свойство линейности не зависит от выбора базиса.
Введем в пространстве прямоугольную декартовую систему координат Охуz так, чтобы плоскость σ совпала с координатной плоскостью Оху. Тогда проекция вектора на плоскость σ будет совпадать с его проекцией на коорди-
натную плоскость Оху: прσ a = прOxy a .
Пусть i, j,k – орты координатных осей Ох, Оу и Oz со-
ответственно. Разложим вектор a по базису {i, j,k}. z
zk
a = xi + yj + zk
|
yj |
у |
||||||||
|
xi |
|||||||||
|
х |
xy |
||||||||
|
пр |
a |
= xi + yj |
|||||||
Рис. 2.
Пусть a = xi + yj + zk . Тогда, как легко видеть из рисунка 2,
прOxy a = xi + yj.
Так как вектор однозначно определяется своими координатами, мы можем отождествить вектор с упорядоченным набором его координат. Теперь, отображение проектирования вектора на данную плоскость можно определить как отображение пространства столбцов высоты 3 в пространство столбцов высоты 2:
прxy : R3 → R2 ,
задаваемое правилом:
43
|
x |
x |
||||
|
прxy |
|||||
|
( y ) = |
. |
||||
|
y |
|||||
|
z |
Теперьможно провести формальное доказательство теоремы.
|
Пусть |
= x1 i + y1 |
= x2 i + y2 |
– произ- |
||||||||||||||||||||||||||||||
|
a |
j+z1 k, |
b |
j+z2 k |
||||||||||||||||||||||||||||||
|
вольные векторы, тогда |
|||||||||||||||||||||||||||||||||
|
x |
1 |
+ x |
2 |
x1 |
+ x2 |
||||||||||||||||||||||||||||
|
+ y2 |
= |
||||||||||||||||||||||||||||||||
|
прOxy (a +b) = прOxy ( y1 |
) = |
+ y2 |
|||||||||||||||||||||||||||||||
|
z |
+z |
2 |
y1 |
||||||||||||||||||||||||||||||
|
1 |
|||||||||||||||||||||||||||||||||
|
x |
1 |
x |
2 |
||||||||||||||||||||||||||||||
|
= прOxy a +прOxy b . |
|||||||||||||||||||||||||||||||||
|
= |
+ |
||||||||||||||||||||||||||||||||
|
y1 |
y2 |
Аналогично доказывается свойство однородности:
λx1
прOxy (λa) = прOxy ( λy1 )
λz1
Задача 254. Найти матрицу проектирования вектора на координатную плоскость.
Решение. Отождествим пространство векторов V3 с
пространством столбцов R3 , и пространство векторов, лежащих на координатной плоскости Оху, с пространством
столбцов R2 . По результатам предыдущей задачи, отображение проектирования на координатную плоскость Оху
есть линейное отображение прxy : R3 → R2 , определенное правилом:
|
x |
x |
|||||||||||||||
|
a = xi + yj + zk , |
прxy a = прxy |
|||||||||||||||
|
( y ) = . |
||||||||||||||||
|
y |
||||||||||||||||
|
z |
||||||||||||||||
|
44 |

Легко видеть, что это отображение задается умножением
|
1 |
0 |
0 |
x |
|||||
|
R |
3 |
: |
||||||
|
матрицы P = |
0 |
1 |
0 |
на столбец X = y |
||||
|
z |
|
1 |
0 |
0 |
x |
x |
|
|
P X = |
0 |
1 |
0 |
y |
= . |
|
y |
|||||
|
z |
Следовательно, матрица Р и есть искомая матрица отображения проектирования на плоскость Оху относительно ба-
зиса {i, j,k} пространства векторов и базиса {i, j} пространства векторов координатной плоскости Оху.
|
1 |
0 |
0 |
– матрица проектирования на коор- |
|
|
Ответ: P = |
0 |
1 |
0 |
|
динатную плоскость Оху.
Замечание. Отображение проектирования вектора на плоскость можно рассматривать как линейный оператор
прσ : V3 → V3 .
В частности, проекция вектора координатного пространства на координатную плоскость Оху прxy : R3 → R3 можно
|
x |
x |
||||||||||||
|
задать правилом: |
|||||||||||||
|
прxy |
|||||||||||||
|
( y ) |
= y . В этом случае матрица |
||||||||||||
|
0 |
|||||||||||||
|
z |
|||||||||||||
|
оператора проектирования |
относительно базиса {i, |
||||||||||||
|
j,k} |
|||||||||||||
|
имеет вид: |
|||||||||||||
|
1 |
0 |
0 |
|||||||||||
|
0 |
1 |
0 |
|||||||||||
|
P = |
. |
||||||||||||
|
0 |
0 |
0 |
|||||||||||
|
45 |
Задача 255. Доказать, что симметрия вектора координатного пространства относительно одной из координатных плоскостей есть линейный оператор, и найти его матрицу.
Решение. Пусть Oxyz координатное пространство с ортонормированным базисом {i, j,k}. Устроим отображение
|
Sxy : V3 → V3 |
по правилу: |
a |
V3 |
положим по определе- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
нию Sxy (a) |
a′, где вектор |
a′ |
симметричен вектору |
a |
от- |
||||||||||||||||||||||||||||||||||||||||||||||
|
носительно координатной плоскости Оху. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Разложим векторы |
и |
по базису {i, |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
a′ |
j,k}: |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
′ |
′ |
′ |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
a = xi + yj+zk, |
a |
′ |
k . |
||||||||||||||||||||||||||||||||||||||||||||||||
|
= x i |
+ y j+z |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
′ |
′ |
′ |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
k . Из |
геометрических |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Тогда Sxy (xi + yj + zk) = x i |
+ y |
j + z |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
соображений ясно, что x′ = x, y′ = y, z′ = −z : |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
z |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
zk |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
a = xi + yj + zk |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
yj |
у |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
xi |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
х |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
′ |
′ |
′ |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
′ |
k |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
= x i + y |
j + z |
Рис. 3.
Отождествляя вектор со столбцом его координат, можно отображение симметрии Sxy задать как отображение
46
Sxy : R3 → R3 , устроенное по правилу:
|
x |
x |
|||||||
|
= a′. |
||||||||
|
Sxy (a) =Sxy ( y ) = |
y |
|||||||
|
z |
−z |
Теперь, как и в задаче 253, легко проверить свойства линейности:
1)a, b V3 , Sxy (a + b) =Sxy (a) +Sxy (b) ;
2)a V3 , λR , Sxy (λa) = λSxy (a) .
Оставим это читателю в качестве легкого упражнения. Легко проверить, что отображение Sxy : R3 → R3 можно
задать с помощью матрицы
|
1 |
0 |
0 |
||
|
0 |
1 |
0 |
||
|
S = |
||||
|
0 |
0 |
|||
|
−1 |
Действительно,
|
1 0 |
0 x |
x |
||||||
|
0 |
1 |
0 |
=Sxy (X) . |
|||||
|
S X = |
y |
= |
y |
|||||
|
0 |
0 |
|||||||
|
−1 z |
−z |
Следовательно, матрица S является матрицей линейного оператора Sxy относительно канонического базиса про-
|
странства столбцов |
R3 или относительно базиса { i, |
|||||||||
|
j,k} |
||||||||||
|
пространства V3 . |
||||||||||
|
1 |
0 |
0 |
||||||||
|
Ответ: |
0 |
1 |
0 |
– матрица оператора симметрии от- |
||||||
|
S = |
||||||||||
|
0 |
0 |
|||||||||
|
−1 |
носительно координатной плоскости Оху. 47
Замечание. Матрицу симметрии S относительно координатной плоскости Оху можно найти, используя определение матрицы линейного оператора. Найдем векторы
Sxy (i), Sxy (j), Sxy (k) и разложим их по базису { i, j,k}. Их координаты будут столбцами искомой матрицы:
Sxy (i) = i =1 i +0 j +0 k , Sxy (j) = j = 0 i +1 j +0 k ,
Sxy (k) = −k = 0 i +0 j −1 k .
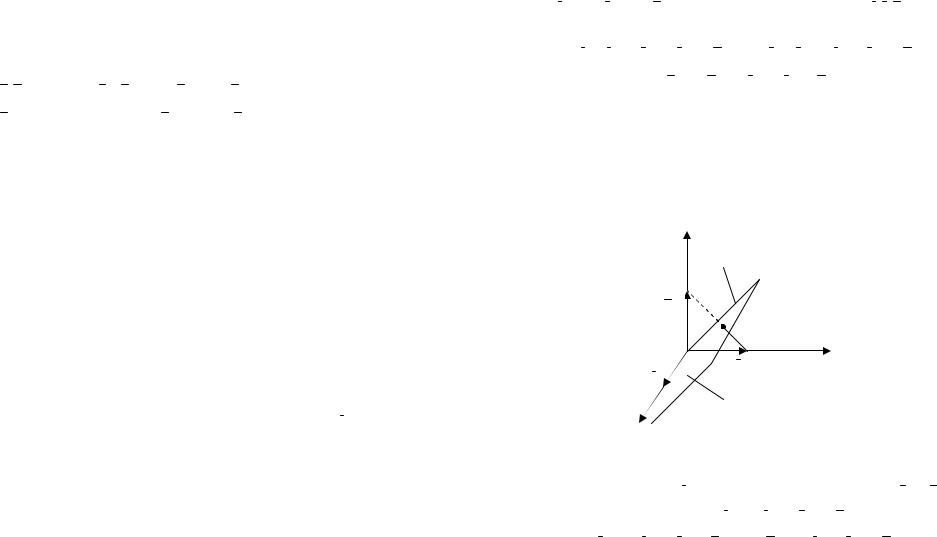
Задача 256. Найдите матрицу оператора симметрии координатного пространства относительно плоскости, проходящей через одну из координатных осей.
Решение. Пусть Sσ : V3 → V3 есть оператор симметрии относительно плоскости σ: y −z = 0 .
z
z = y
k
у
j
i
хσ
Рис. 4.
Нетрудно видеть, что при симметрии относительно данной плоскости σ, вектор i остается на месте, а векторы j и k переходят друг в друга: Sσ (i) =1 i +0 j +0 k ,
Sσ ( j) = 0 i +0 j +1 k , Sσ (k) = 0 i +1 j +0 k . 48
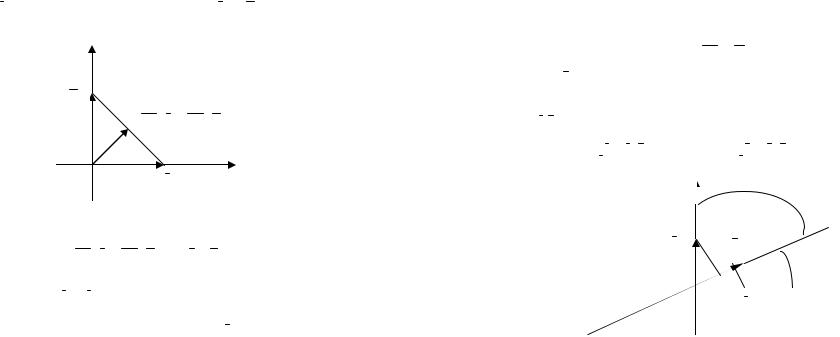
|
1 |
0 |
0 |
|||
|
Ответ: Sσ |
0 |
0 |
1 |
||
|
= |
. |
||||
|
0 |
1 |
0 |
|||
Задача 257. Найдите матрицу оператора проектирования вектора координатного пространства на плоскость, проходящую через одну из координатных осей.
Решение. Пусть Pσ : V3 → V3 есть оператор проектирования на плоскость σ: y −z = 0 . Воспользуемся рисунком 4. Ясно, что при проектировании на данную плоскость, вектор i остается на месте, а векторы j и k проектируются на прямую y = z в плоскости Oyz:
z
k
прσ j = прσ k
у
j
Рис. 5.
Легко видеть, что прσ j = прσ k = 12 (j + k) . Таким образом,
|
1 |
1 |
. |
||||||||||||
|
Pσ(i) =i, Pσ (j) = Pσ(k) = |
j+ |
k |
||||||||||||
|
2 |
2 |
|||||||||||||
|
Записывая координаты векторов |
Pσ(i), |
Pσ( |
||||||||||||
|
j), Pσ(k) по |
столбцам, получаем матрицу проектирования на данную плоскость.
49
|
1 |
0 |
0 |
2 |
0 |
0 |
||||||
|
Ответ: P |
= |
0 |
1 |
1 |
= |
1 |
0 |
1 |
1 |
. |
|
|
σ |
2 |
2 |
2 |
||||||||
|
0 |
1 |
1 |
|||||||||
|
1 |
1 |
||||||||||
|
0 |
|||||||||||
|
2 |
2 |
Задача 258. Найдите матрицу оператора проектирования вектора координатной плоскости на прямую, проходящую через начало координат.
Решение. Пусть в ПДСК Oxy дано каноническое уравнение прямой, проходящей через начало координат
L : mx = ny .
Пусть so = (cos α,cosβ) есть единичный направляющий вектор данной прямой. Находим проекции базисных векто-
ров i, j на данную прямую:
прs i = i so = cos α, прs j = j so = cosβ.
уβ
j so
α
i
Рис. 6.
Обозначим оператор проектирования на данную прямую через PL : V2 → V2 . Тогда
50
PL (i) = (cos α) so = (cos2 α,cosα cosβ) ,
PL (j) = (cosβ) so = (cosβ cos α,cos2 β) .
Координаты этих векторов образуют столбцы матрицы оператора PL :
|
PL |
2 |
α |
cos α cosβ |
||||
|
= cos |
. |
||||||
|
cos α cosβ cos2 |
β |
||||||
|
2 |
α |
cos α cosβ |
|||||
|
Ответ: PL = cos |
. |
||||||
|
cos α cosβ |
cos2 β |
Задача 259. Найдите матрицу оператора проектирования вектора координатного пространства на прямую, проходящую через начало координат.
Решение. Пусть в ПДСК Oxyz дано уравнение прямой, проходящей через начало координат:
L : mx = ny = pz .
Пусть, далее, (cos α,cosβ,cos γ) – направляющие косинусы направляющего вектора прямой s = (m,n,p) . Тогда вектор
so = (cos α,cosβ,cos γ) – единичный направляющий вектор данной прямой. Находим проекции базисных векторов
i, j,k на данную прямую:
прs i = i so = cos α, прs j = j so = cosβ, прs k = k so = cos γ .
Обозначим оператор проектирования на данную прямую через PL : V3 → V3 . Тогда
|
P (i) = (cos α) |
o |
, |
P (j) = (cosβ) |
o |
, |
P (k) = (cos γ) |
o . |
|||
|
s |
s |
s |
||||||||
|
L |
L |
L |
Координаты этих векторов образуют столбцы матрицы оператора PL .
51
|
cos2 α |
cos αcosβ |
cos α cos γ |
||||||
|
Ответ: P |
= |
cos α cosβ |
cos2 β |
cosβ cos γ |
. |
|||
|
L |
||||||||
|
cosβcos γ |
cos |
2 |
γ |
|||||
|
cos α cos γ |
Задача 260. Доказать, что дифференцирование многочленов есть линейное отображение, и найти его матрицу, если степени многочленов не превышают числа n.
Решение. Пусть Kn [x] – векторное пространство мно-
гочленов над полем K, степень которых не превышает натурального числа n. Легко видеть, что система многочле-
нов {1, x, x2 ,…, xn } является базисом пространства Kn [x] , так что dim Kn [x] = n +1 . Устроим отображение
D : Kn [x] → Kn−1[x]
по правилу:
f (x) = ao +a1x +a2 x2 +…+an xn Kn
положим по определению
D(f (x)) = a1 + 2a2 x +… + nan xn−1 Kn−1[x] .
Отображение D называется отображением дифференцирования.
В силу свойств дифференцирования, для любых многочленов f(x) и g(x), и для любого скаляра λ выполняются равенства:
D(f +g) = D(f ) + D(g) и D(λf ) = λD(f ) ,
из которых следует, что отображение D является линейным. Заметим, впрочем, что эти равенства можно проверить непосредственно, пользуясь нашим определением отображения дифференцирования.
Найдем матрицу отображения D относительно базисов
{1, x, x2 ,…, xn } пространства Kn [x] и {1, x, x2 ,…, xn−1} про-
странства Kn−1[x]. С этой целью, продифференцируем ба52
зисные векторы пространства Kn [x] и разложим получившиеся многочлены по базису пространства Kn−1[x]:
D(1) = 0 = 0 1+0 x +… +0 xn−1 , D(x) =1 =1 1+0 x +… +0 xn−1 , D(x2 ) = 2x = 0 1+ 2 x +… +0 xn−1 ,
……………………………………
D(xn ) = nxn−1 = 0 1+0 x +…+n xn−1 .
Координаты многочленов D(1), D(x), D(x2 ) ,…, D(xn ) об-
разуют столбцы матрицы линейного отображения D, которую мы будем обозначать тоже буквой D:
|
0 |
1 |
0 … |
0 |
||
|
0 |
0 |
2 … |
0 |
||
|
D = |
. |
||||
|
… … |
… … |
… |
|||
|
0 |
0 |
0 … |
n |
||
Как легко видеть, матрица отображения дифференцирования имеет размеры n ×(n +1) .
Пример. Найти матрицу дифференцирования многочленов, степень которых не превышает числа 3.
Решение. D : K3[x] → K2[x] , {1, x, x2 , x3} – базис K3[x] , {1, x, x2} – базис K2 [x] и
D(1) = 0, D(x) =1, D(x2 ) = 2x, D(x3 ) = 3x2 .
Раскладывая эти многочлены по базису {1, x, x2 }, получаем: D(1) = 0 = 0 1+0 x +0 x2 ,
D(x) =1 =1 1+0 x +0 x2 ,
D(x2 ) = 2x = 0 1+ 2 x +0 x2 ,
D(x3 ) = 3x2 = 0 1+0 x +3 x2 .
53
Коэффициенты разложения по базису образуют столбцы искомой матрицы.
|
0 |
1 |
0 |
0 |
|||
|
Ответ: |
0 |
0 |
2 |
0 |
||
|
D = |
. |
|||||
|
0 |
0 |
0 |
3 |
|||
Замечание. Отображение дифференцирования
D : Kn [x] → Kn−1[x]
можно рассматривать как линейный оператор, определенный на векторном пространстве многочленов над полем K степени не выше n:
D : Kn [x] → Kn [x] .
Тогда, матрица D этого оператора относительно базиса {1, x, x2 ,…, xn } пространства Kn [x] будет иметь вид:
|
0 |
1 |
0 |
… |
0 |
||
|
0 |
0 |
2 |
… |
0 |
||
|
D = … … |
… … |
… . |
||||
|
0 |
0 |
0 |
… |
n |
||
|
0 |
0 |
0 |
… |
0 |
||
В частности, матрица оператора дифференцирования в примере имеет вид:
|
0 |
1 |
0 |
0 |
||
|
0 |
0 |
2 |
0 |
||
|
D = |
. |
||||
|
0 |
0 |
0 |
3 |
||
|
0 |
0 |
0 |
0 |
||
Задача 260. Докажите, что умножение комплексного числа на фиксированное комплексное число есть линейный оператор, и найдите его матрицу.
54
Решение. Пусть C ={x +iy | x, y R} – поле комплекс-
ных чисел, которое мы будем рассматривать как векторное пространство над полем действительных чисел R.
Пусть zo C – произвольное, фиксированное комплексное число. Устроим отображение f : C → C по правилу:
z C, f (z) z zo
и докажем, что f – линейный оператор.
Действительно, пусть z,z1 ,z2 C – произвольные ком-
плексные числа, λ R – произвольное действительное число. Тогда
f (z1 +z2 ) = (z1 +z2 ) zo = z1zo +z2zo = f (z1 ) +f (z2 ) , f (λz) = (λz) zo = λ(zzo ) = λf (z) ,
т.е. отображение f аддитивное и однородное, ч.т.д. Найдем матрицу этого линейного оператора относи-
тельно базиса {1,i}. Пусть zo = a + bi . Найдем f (1), f (i) и разложим их по базису {1,i}:
f (1) =1 zo = a +bi, f (i) = i zo = i(a +bi) = −b +ai .
Из определения матрицы линейного оператора следует, что коэффициенты этих разложений образуют ее столбцы:
Таким образом, матрица А является матрицей данного линейного оператора относительно стандартного базиса {1,i}
векторного пространства С над полем R.
Пусть {z1,z2} – произвольный базис пространства С, где z1 = α+βi, z2 = γ+δi . Тогда матрица
есть матрица перехода от старого базиса {1,i} к новому базису {z1,z2}. Тогда матрица линейного оператора отно-
|
сительно нового базиса имеет вид: |
|||||||
|
A′ = D−1AD , |
|||||||
|
A′ = |
1 |
δ −γ a |
−b α |
γ |
|||
|
. |
|||||||
|
a |
β |
||||||
|
αδ−βγ |
−β α b |
δ |
Пример. Найти матрицу линейного оператора умножения на мнимую единицу в пространстве комплексных чисел относительно базиса {z1,z2}, где
|
z1 = cos ϕ+isin ϕ, |
|||||||||
|
z2 |
ϕ+ |
π |
ϕ+ |
π |
= −sin ϕ+icos ϕ. |
||||
|
= cos |
+isin |
2 |
|||||||
|
2 |
|||||||||
|
Решение. В данном случае, |
zo |
= 0 |
+1 i и a = 0, b =1, мат- |
рица оператора относительно базиса {1,i} имеет вид:
|
0 |
−1 |
||||||||
|
A = |
. |
||||||||
|
1 |
0 |
||||||||
|
Матрица перехода и обратная к ней имеют вид: |
|||||||||
|
cos ϕ |
−sin ϕ |
cos ϕ |
sin ϕ |
||||||
|
D = |
, D−1 = |
. |
|||||||
|
sin ϕ |
cos ϕ |
−sin ϕ |
cos ϕ |
||||||
|
Матрица оператора в новом базисе |
|||||||||
|
cos ϕ |
sin ϕ 0 |
−1 cos ϕ |
−sin ϕ |
= |
|||||
|
A′ = |
−sin ϕ |
cos ϕ |
|||||||
|
cos ϕ 1 |
0 sin ϕ |
||||||||
|
sin ϕ |
−cos ϕ cos ϕ |
−sin ϕ |
0 |
−1 |
= A . |
||||
|
= |
= |
||||||||
|
cos ϕ |
sin ϕ sin ϕ |
cos ϕ |
1 |
0 |
|||||
|
Ответ: |
0 |
−1 |
|||||||
|
0 |
. |
||||||||
|
1 |
|||||||||
|
56 |

Замечание 1. Из геометрической интерпретации комплексных чисел следует, что комплексное число можно отождествить с вектором плоскости. Умножение комплексного числа на мнимую единицу приводит к повороту
вектора на 90o против часовой стрелки. Действительно, запишем произвольное комплексное число в тригонометрической форме записи:
z =| z | (cos α+isin α) ,
где α = arg z . Тогда
|
z i =| z | (cos α+isin α) (cos |
π |
+isin |
π) = |
||||
|
π |
2 |
π |
2 |
||||
|
α+ |
α+ |
||||||
|
=| z | (cos |
+isin |
2 |
) . |
||||
|
2 |
Мы видим, что аргумент комплексного числа после умножения на мнимую единицу увеличивается на π/ 2 , модуль остается прежним. Следовательно, оператор умножения на мнимую единицу есть оператор поворота соответствующе-
го вектора на 90o против часовой стрелки.
Результаты примера говорят о том, что матрица поворо-
та на 90o остается неизменной при переходе к новому базису, полученного поворотом старого базиса на произвольный угол ϕ. Можно доказать, что при этом останется не-
изменной и матрица умножения на любое фиксированное комплексное число zo = a + bi . См. следующее замечание.
Замечание 2. Заметим, что умножение комплексного числа z на комплексное число zo = a + bi приводит к повороту
соответствующего вектора z на угол α, где α = arg zo и растяжению (сжатию) его в | zo | раз. Действительно, пусть z =| z | (cos ϕ+isin ϕ) – тригонометрическая форма записи
57
комплексного числа z, а zo =| zo | (cos α+isin α) – тригонометрическая форма записи комплексного числа zo = a + bi ,
где a =| zo | cos α, b =| zo | sin α . Тогда
z zo =| z | | zo | (cos(ϕ+α) +isin(ϕ+α)) .
Таким образом, матрицу умножения на комплексное число zo можно записать в виде
|
cos α |
−sin α |
||||||
|
A =| zo | |
α |
. |
|||||
|
sin |
cos α |
||||||
|
Отсюда получаем, что |
|||||||
|
A′ = D−1AD = |
|||||||
|
=| zo |
cos ϕ |
sin ϕ cos α |
−sin α cos ϕ |
−sin ϕ |
= |
||
|
| |
cos α |
||||||
|
−sin ϕ |
cos ϕ sin α |
sin ϕ |
cos ϕ |
||||
|
cos α |
−sin α |
= A . |
|||||
|
=| zo | |
|||||||
|
sin α |
cos α |
Произведение матриц поворота геометрически можно интерпретировать так, что сначала вектор z поворачивается на угол ϕ, затем на угол α, затем на угол ( −ϕ) и затем из-
меняется его модуль. В результате мы получаем, что вектор поворачивается на угол α с последующим изменением его модуля.
Задача 262. Докажите, что отображение, которое каждому комплексному числу ставит в соответствие комплексно сопряженное ему число есть линейный оператор. Найдите его матрицу относительно естественного базиса пространства комплексных чисел.
Решение. Пусть отображение f : C → C устроено по
правилу: z = x +iy C , f (z) z = x −iy .
Докажем линейность этого отображения. 58

1) Пусть z1 = x1 +iy1, z2 = x2 +iy2 – два произвольных
комплексных числа. Тогда
z1 +z2 = (x1 +x2 ) +i(y1 + y2 ) ,
f (z1 +z2 ) = (x1 + x2 ) +i (y1 + y2 ) = (x1 + x2 ) −i (y1 + y2 ) =
=(x1 −iy1 ) +(x2 −iy2 ) = z1 + z2 = f (z1 ) +f (z2 ) .
2)Пусть λ R – произвольное действительное число.
Тогда
f (λz) = λz = λx +iλy = λx −iλy = λ(x −iy) = λz = λf (z) .
Линейный оператор f будем называть оператором сопряжения. Найдем матрицу оператора сопряжения относительно базиса {1,i} векторного пространства комплексных
чисел. Воспользуемся определением матрицы линейного оператора относительно данного базиса, и найдем образы базисных векторов, т.е. найдем сопряженные им числа:
f (1) =1+0 i =1−0 i, f (i) = 0 +i = 0 −i .
Столбцы координат векторов f (1), f (i) образуют столбцы искомой матрицы оператора сопряжения.
Задача 263. Докажите, что умножение вектора на фиксированный скаляр есть линейный оператор, и найдите его матрицу.
Решение. Пусть α K – произвольный фиксированный скаляр, V – произвольное векторное пространство над полем K. Устроим отображение
fα : V → V
по правилу: x V положим по определению fα (x) α x . Докажем, что fα является линейным оператором.
59
Пусть x, y V – произвольные векторы, λ K – произвольный скаляр. Тогда
1)fα (x + y) = α (x + y) = α x +α y = fα (x) +fα (y) ,
2)fα (λx) = α (λx) = (αλ) x = (λα) x = λ(α x) = λfα (x) .
Мы использовали аксиомы векторного пространства и поля. Найдем матрицу линейного оператора fα относительно
какого-нибудь базиса {e1,e2 ,…,en } векторного пространст-
ва V. Найдем образы базисных векторов и разложим их по этому же базису. Для любого i =1,2,…,n получаем:
fα (ei ) = α ei = 0 e1 +… +0 ei−1 +α ei +0 ei+1 +… +0 en .
Столбцы координат образуют столбцы искомой матрицы.
|
α |
0 |
… |
0 |
|||
|
0 |
α |
… |
0 |
|||
|
Ответ: A = |
= αE . |
|||||
|
… |
… |
… |
… |
|||
|
0 |
0 |
… |
||||
|
α |
Задача 264. Найдите матрицу оператора проектирования на подпространство L пространства V параллельно подпространству М, если пространство V есть прямая сумма подпространств М и L.
Решение. Пусть V – векторное пространство над полем K, L и М – его подпространства, причем
V = L M .
Пусть {e1,e2 ,…,ek } – произвольный базис подпространства L, {f1,f2 ,…,fm} – произвольный базис подпространства М.
|
Тогда, по определению |
прямой суммы, следует, что |
|
{e1,e2 ,…,ek ,f1,f2 ,…,fm} – |
базис пространства V, и любой |
вектор z V можно единственным образом представить в виде z = x + y , где
60
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Оператор Проектирования. Пусть требуется найти матрицу линейного оператора, осуществляющего проектирование трехмерного пространства на координатную ось Е1 в базисе Е1, Е2, Е3. Матрица линейного оператора – это матрица, в столбцах которой должны стоять образы базисных векторов Е1 = (1,0,0), Е2 = (0,1,0), Е3 = (0,0,1). Эти образы, очевидно, есть: Ае1 = (1,0,0)
Ае2 = (0,0,0)
Ае3 = (0,0,0)
Следовательно, в базисе Е1, Е2, Е3 матрица искомого линейного оператора будет иметь вид:
Найдем ядро этого оператора. Согласно определению ядро – это множество векторов Х, для которых АХ = 0. Или

Т. е. ядро оператора составляет множество векторов, лежащих в плоскости Е1, Е2. Размерность ядра равна n – rangA = 2.
Множество образов этого оператора – это, очевидно, множество векторов, коллинеарных Е1. Размерность пространства образов равна рангу линейного оператора и равна 1, что меньше размерности пространства прообразов. Т. е. оператор А – вырожденный. Матрица А тоже вырождена.
Еще пример: найти матрицу линейного оператора, осуществляющего в пространстве V3 (базис I, J, K) линейное преобразование – симметрию относительно начала координат.
Имеем: Ai = — i
Aj = — j
Ak = — k
Т. е. искомая матрица
Рассмотрим линейное преобразование – Симметрию относительно плоскости Y = X.
Ai = j (0,1,0)
Aj = I (1,0,0)
Ak = K (0,0,1)
Матрица оператора будет:
Ai Aj Ak

Ai ’ = cosjI + sinjJ
Aj ’ = — sinjI + cosjJ
Матрица оператора поворота:
Ai ‘ Aj ‘
Вспомним формулы преобразования координат точки при смене базиса – замена координат на плоскости при смене базиса:


Параллельный перенос обеспечивает соотношения:
Для того, чтобы решить такую задачу, обычно применяют искусственный прием: вводят так зазываемые “однородные” координаты точки на плоскости XOY: (x, y, 1). Тогда матрица, осуществляющая параллельный перенос, может быть записана:
Действительно:
А матрица поворота:
Рассматриваемая задача может быть решена в три шага:
1й шаг: параллельный перенос на вектор А(-а, — b) для совмещения центра поворота с началом координат:
2й шаг: поворот на угол j:
3й шаг: параллельный перенос на вектор А(а, b) для возвращения центра поворота в прежнее положение:
Искомое линейное преобразование в матричном виде будет выглядеть:

Где
По формуле (**) можно пересчитать координаты любой точки плоской фигуры, а затем построить ее на экране, осуществив тем самым ее поворот.
| < Предыдущая | Следующая > |
|---|
Пусть нам требуется найти проекцию вектора $%(x,y,z)$% на заданную плоскость. Обозначим вектор проекции через $%(x_1,y_1,z_1)$%. Разность этих двух векторов перпендикулярна плоскости, поэтому она пропорциональна вектору нормали, и для какого-то значения параметра $%t$% пропорциональна вектору $%(4;2;-5)$% из коэффициентов уравнения. Следовательно, достаточно найти такое $%t$%, что вектор $%(x_1,y_1,z_1)=(x-4t,y-2t,z+5t)$% будет принадлежать плоскости, то есть он удовлетворяет её уравнению: $%4(x-4t)+2(y-2t)-5(z+5t)=0$%. Таким образом, $%t=frac{4x+2y-5z}{4^2+2^2+5^2}$%. Подставляя найденное значение в равенство $%(x_1,y_1,z_1)=(x-4t,y-2t,z+5t)$%, выражаем через $%x$%, $%y$%, $%z$% координаты вектора проекции. Например, $%x_1=x-frac{4(4x+2y-5z)}{45}=frac{29}{45}x-frac8{45}y+frac49z$%. Это будет первый столбец матрицы проектирования. Аналогично находим второй и третий.
Собственные подпространства находим из геометрических соображений. Достаточно сказать про одномерные и двумерные, то есть про прямые и плоскости. Собственные прямые — это прямые плоскости проектирования (они проектируются в себя), а также перпендикуляр к плоскости. Единственная собственная плоскость — это плоскость проектирования.














