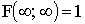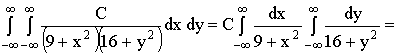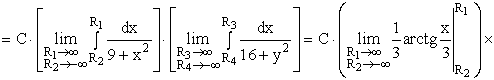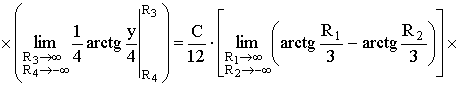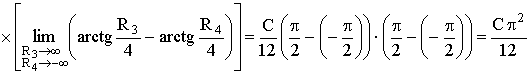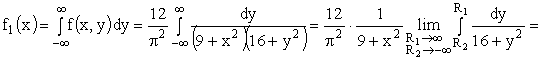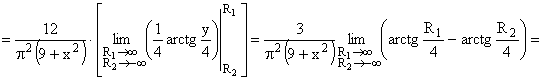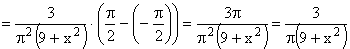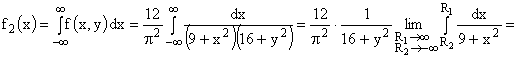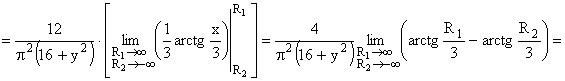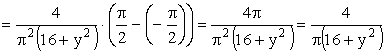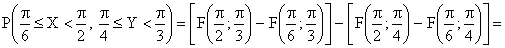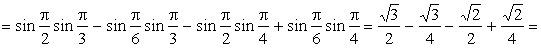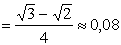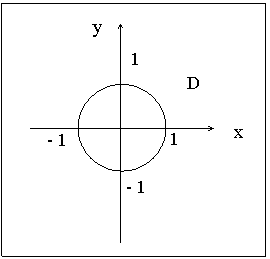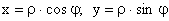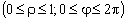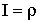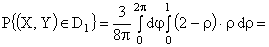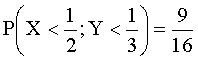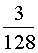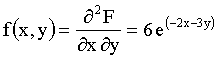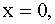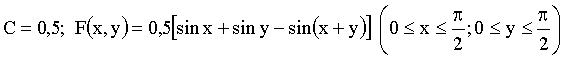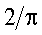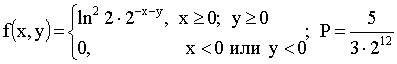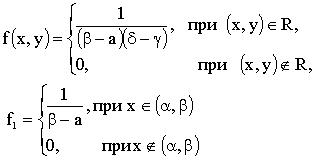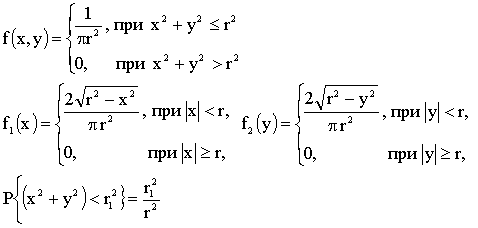Как найти матрицу распределения

Двухмерная
случайная величина (Х,Y)
является дискретной, если множества
значений ее компонент _X
и _Y
представляют
собой счетные множества. Для описания
вероятностных характеристик таких
величин используется двухмерная функция
распределения и матрица распределения.

Матрица
распределения
представляет собой прямоугольную
таблицу, которая содержит

значения
компоненты X

_X=x₁,x₂,..
x_n,

значения
компоненты Y

_Y=y₁,y₂,
… y_m

и
вероятности всевозможных пар значений
p_ij
= p(X
=x_i
, Y = y_j ),
i=1..n,
j=1..m.

xi yj	y1	y2	…….	ym
x1	p11	p12	…….	p1m
x2	p21	p22	…….	p2m
…….	…….	…….	…….	…….
xn	pn1	pn2	…….	pnm

Свойства
матрицы распределения
вероятностей:

1.

.

2.
Переход к ряду распределения вероятностей
составляющей X:

. (8.3)

3.
Переход к ряду распределения вероятностей
составляющей Y:

. (8.4)

8.1.3 Двухмерная плотность распределения

Двухмерная
случайная величина (X,Y)
является непрерывной, если ее функция
распределения F(х,у)
представляет собой непрерывную,
дифференцируемою функцию по каждому
из аргументов и существует вторая
смешанная производная
.

Двухмерная
плотность распределения
f(х,у)
характеризует плотность вероятности
в окрестности точки с координатами
(х,у)

и равна второй
смешанной производной функция
распределения:

. (8.5)

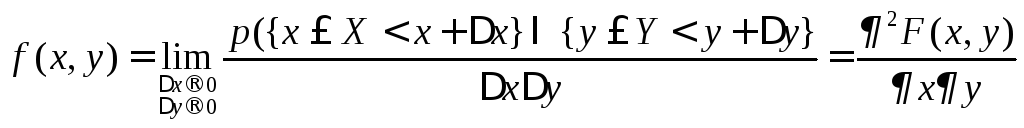
Геометрически
f(х,у)
– это некоторая поверхность
распределения,
она аналогична кривой распределения
для одномерной случайной величины.
Аналогично
можно ввести понятие
элемента вероятности:.
Вероятность попадания значения двухмерной
случайной величины (X,Y)
в произвольную область D
равна сумме
всех элементов вероятности для этой
области:

(8.6)

Свойства двухмерной
плотности :

1.
.

2. Условие нормировки:

. (8.7)

Геометрически
– объем тела, ограниченный поверхностью
распределения и плоскостью x0y,
равен единице.

3. Переход к функции
распределения:

. (8.8)

4. Переход к
одномерным характеристикам:

;
(8.9)

. (8.10)

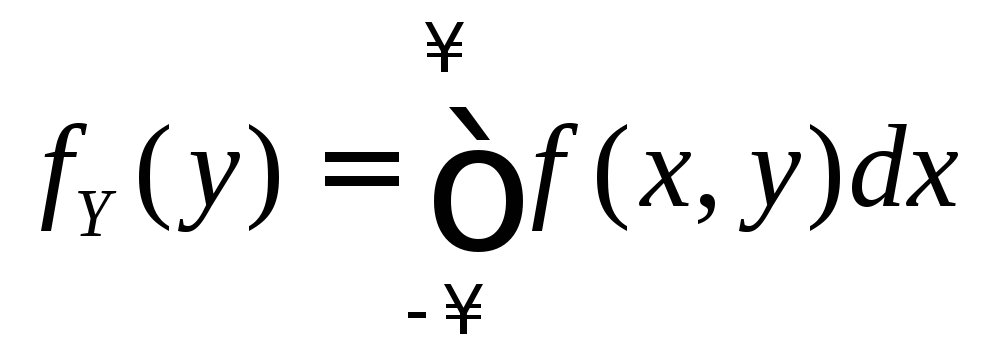
8.2 Зависимые и независимые случайные величины

Величина
Х независима
от величины У, если ее закон распределения
не зависит от того, какое значение
приняла величины У. Для независимых
величин выполняется следующие соотношения,
т. е. критерии независимости:

1)
F(x,y)=p(X<x,Y<y)=p(X<x)p(Y<y)=F_X(x)F_Y(y)

x,
y; (8.11)

2)
для непрерывных-
f(x,
y)
= f_X(x)f_Y(y)

x,
y;
(8.12)

3)
для дискретных —
p_ij
=
p_i
p_j
, для 
i,
j.
(8.13)

В
том случае, если критерии не выполняются
хотя бы в одной точке, величины X
и Y
являются зависимыми. Для независимых
величин двухмерные формы закона
распределения не содержат никакой
дополнительной информации, кроме той,
которая содержится в двух одномерных
законах. Таким образом, в случае
зависимости величин X
и Y,
переход от двух одномерных законов к
двухмерному закону осуществить
невозможно. Для этого необходимо знать
условные законы распределения.

8.3 Условные законы распределения

Условным
законом распределения
называется распределение одной случайной
величины, найденное при условии, что
другая случайная величина приняла
определенное значение.

Условные
ряды распределения
для дискретных составляющих Х
и Y
определяются по формулам:

p_i/j
= p(X
=
x_i/Y
=
y_j)
= p_ij/p(Y
=
y_j),
i
=
1, …, n; (8.14)

p_j/i
= p(Y
=
y_j/X
=
x_i)
= p_ij/p(X
=
x_i),
j
=
1, …, m. (8.15)

Матрица
распределения вероятностей дискретной
двухмерной случайной величины (Х,Y),
если ее компоненты зависимы, “порождает”два
одномерных ряда вероятностей (см. (8.3,
8.4)) и два семейства условных рядов
вероятностей (8.14, 8.15).

Условные
плотности распределения
для непрерывных составляющих X
и Y
определяются по формулам:

f(x/y)
= f(x,
y)/f_Y(y),
для
f_Y
(y)
0;
(8.16)

f(y/x)
= f(x,
y)/f_X(x),
для
f_X
(x)
0. (8.17)

Условные законы
распределения обладают всеми свойствами
соответствующих им одномерных форм
законов распределения.

Если
величины Х
и Y
независимы,
то условные законы распределения равны
соответствующим безусловным:

p_i/j
= p_i,
i
=
1, …, n; (8.18)

p_j/i
= p_j,
j
=
1, …, m. (8.19)

f(x/y)
= f_X(x);
(8.20)

f(y/x)
= f_Y(y). (8.21)

Следует
различать функциональную и статистическую
(вероятностную) зависимости между
случайными величинами. Если Х и Y случайные
величины, которые связаны между собой
функциональной зависимостью у = 
(х), то, зная значение Х, можно точно
вычислить соответствующие значение Y,
и наоборот.

Если
между случайными величинами существует
статистическая
зависимость (величины
Х
и Y
зависимы — см. (8.11 – 8.13)), то по значению
одной из них можно установить только
условное распределение вероятностей
другой, т.е. определить, с какой вероятностью
появится то или иное значение другой
величины.

Пример.
Y—
урожай зерна, Х—
количество удобрений на некотором
участке земли. Очевидно, что между Х
и Y
существует статистическая зависимость,
так как значение Y
(урожайность на участке) зависит и от
многих других факторов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Двумерная дискретная случайная величина

Ранее мы разобрали примеры решений задач для одномерной дискретной случайной величины. Но бывает, что результат испытания описывается не одной, а несколькими случайными величинами (случайным вектором).

В случае двух величин (скажем, $X$ и $Y$) мы имеем дело с так называемой двумерной дискретной случайной величиной $(X,Y)$ (или системой случайных одномерных величин). Кратко выпишем основы теории.

Система двух случайных величин: теория

Двумерная ДСВ задается законом распределения (обычно представленным в виде таблицы распределения):

$$
P(X=x_i, Y=y_k)=p_{ik}, i=1,2,…,m; k=1,2,…,n; quad sum_{i,k}p_{ik}=1.
$$

По нему можно найти одномерные законы распределения (составляющих):

$$
p_i=P(X=x_i)=sum_{k}p_{ik}, i=1,2,…,m; \ p_k=P(Y=y_k)=sum_{i} p_{ik}, k=1,2,…,n.
$$

Интегральная функция распределения задается формулой $F(x,y)=P(Xlt x, Ylt y)$. Даже для самого простого закона распределения 2 на 2 функция занимает 5 строк, поэтому ее редко выписывают в явном виде.

Если для любой пары возможных значений $(X=x_i, Y=y_k)$ выполняется равенство

$$P(X=x_i, Y=y_k)=P(X=x_i)cdot P(Y=y_k),$$

то случайные величины $X, Y$ называются независимыми.

Если случайные величины зависимы, для них можно выписать условные законы распределения (для независимых они совпадают с безусловными законами):

$$
P(X=x_i| Y=y_k)=frac{P(X=x_i, Y=y_k)}{P(Y=y_k)},\
P(Y=y_k| X=x_i)=frac{P(X=x_i, Y=y_k)}{P(X=x_i)}.
$$

Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:

$$
cov (X,Y)=M(XY)-M(X)M(Y), quad r_{XY} = frac{cov(X,Y)}{sqrt{D(X)D(Y)}}.
$$

Далее вы найдете разные примеры задач с полным решением, где используются дискретные двумерные случайные величины (системы случайных величин).

Примеры решений

Задача 1. В продукции завода брак вследствие дефекта А составляет 10%, а вследствие дефекта В — 20%. Годная продукция составляет 75%. Пусть X — индикатор дефекта А, a Y — индикатор дефекта В. Составить матрицу распределения двумерной случайной величины (X, Y). Найти одномерные ряды распределений составляющих X и У и исследовать их зависимость.

Задача 2. Два баскетболиста по два раза бросают мяч в корзину. При каждом броске вероятность попадания для первого баскетболиста 0,6, для второго – 0,7. Случайная величина X – число попаданий первым баскетболистом по кольцу. Случайная величина Y – суммарное число попаданий обоими баскетболистами. Построить таблицу распределения случайного вектора (X,Y). Найти характеристики вектора (X,Y). Зависимы или независимы случайные величины X и Y.

Задача 3. Слово РОССИЯ разрезано по буквам. Случайным образом вынимаем две буквы, тогда X – количество гласных среди них, затем вынимаем еще две буквы и Y – количество гласных во второй паре. Составить закон распределения системы случайных величин X, Y.

Задача 4. $X, Y$ — индикаторы событий $A, B$, означающий положительные ответы соответственно на вопросы $alpha, beta$ социологической анкеты. По данным социологического опроса двумерная случайная величина $(X,Y)$ имеет следующую таблицу распределения.
Положительному ответу присвоен ранг 1, отрицательному – 0.
Найти коэффициент корреляции $rho_{XY}$.

Задача 5. Составить закон распределения X — сумм очков и Y — числа тузов при выборе двух карт из колоды, содержащей только тузов, королей и дам (туз=11, дама=3, король=4)
Найти законы распределения величин Х и Y. Зависимы ли эти величины? Написать функцию распределения для (Х, Y). Построить ковариационный граф. Посчитать ковариацию (X,Y). Написать ковариационную матрицу. Посчитать корреляцию (X,Y) и написать корреляционную матрицу.

Задача 6. Бросаются две одинаковые игральные кости. Случайная величина X равна 1, если сумма выпавших чисел четна, и равна 0 в противном случае. Случайная величина Y равна 1, если произведение выпавших чисел четно, и 0 в противном случае. Описать закон распределения случайного вектора (X,Y). Найти D[X], D[Y] и cov[X,Y].

Задача 7. В урне лежат 100 шаров, из них 25 белых. Из урны последовательно вынимают два шара. Пусть $X_i$ – число белых шаров, появившихся при $i$-м вынимании. Найти коэффициент корреляции между величинами $X_1$ и $X_2$.

Задача 8. Для заданного закона распределения вероятностей двухмерной случайной величины (Х, Y):
YX 2 5
8 0,15 0,10
10 0,22 0,23
12 0,10 0,20
Найти коэффициент корреляции между величинами Х и Y.

Задача 9. Задана дискретная двумерная случайная величина (X,Y).
А) найти безусловные законы распределения составляющих;
Б) построить регрессию случайной величины Y на X;
В) построить регрессию случайной величины X на Y;
Г) найти коэффициент ковариации;
Д) найти коэффициент корреляции.
20 30 40 50 70
3 0,01 0,01 0,02 0,02 0,01
4 0,04 0,3 0,06 0,03 0,01
5 0,02 0,03 0,06 0,07 0,05
9 0,05 0,03 0,04 0,02 0,03
10 0,03 0,02 0,01 0,01 0,02

Задача 10. Система (x, y) задана следующей двумерной таблицей распределения вероятностей. Определить:
А) безусловные законы распределения составляющих;
Б) условный закон распределения y при x=1;
В) условное математическое ожидание x при y=2.

Г) вероятность того, что случайная величина (x,y) будет принадлежать области $|x|+|y|le 3$.

-3 0 2
-1 0 0,1 0,15
1 0,05 0,3 0,05
2 0,15 0,05 0,15

Решебник по теории вероятности онлайн

Больше 11000 решенных и оформленных задач по теории вероятности:

From Wikipedia, the free encyclopedia

Matrix normal

Notation
Parameters	location (real matrix) scale (positive-definite real matrix) scale (positive-definite real matrix)
Support
PDF
Mean
Variance	(among-row) and (among-column)

In statistics, the matrix normal distribution or matrix Gaussian distribution is a probability distribution that is a generalization of the multivariate normal distribution to matrix-valued random variables.

Definition[edit]

The probability density function for the random matrix X (n × p) that follows the matrix normal distribution has the form:

where denotes trace and M is n × p, U is n × n and V is p × p, and the density is understood as the probability density function with respect to the standard Lebesgue measure in , i.e.: the measure corresponding to integration with respect to .

The matrix normal is related to the multivariate normal distribution in the following way:

if and only if

where denotes the Kronecker product and denotes the vectorization of .

Proof[edit]

The equivalence between the above matrix normal and multivariate normal density functions can be shown using several properties of the trace and Kronecker product, as follows. We start with the argument of the exponent of the matrix normal PDF:

which is the argument of the exponent of the multivariate normal PDF with respect to Lebesgue measure in . The proof is completed by using the determinant property:

Properties[edit]

If , then we have the following properties:^[1][2]

Expected values[edit]

The mean, or expected value is:

and we have the following second-order expectations:

where denotes trace.

More generally, for appropriately dimensioned matrices A,B,C:

Transformation[edit]

Transpose transform:

Linear transform: let D (r-by-n), be of full rank r ≤ n and C (p-by-s), be of full rank s ≤ p, then:

Example[edit]

Let’s imagine a sample of n independent p-dimensional random variables identically distributed according to a multivariate normal distribution:

.

When defining the n × p matrix for which the ith row is , we obtain:

where each row of is equal to , that is , is the n × n identity matrix, that is the rows are independent, and .

Maximum likelihood parameter estimation[edit]

Given k matrices, each of size n × p, denoted , which we assume have been sampled i.i.d. from a matrix normal distribution, the maximum likelihood estimate of the parameters can be obtained by maximizing:

The solution for the mean has a closed form, namely

but the covariance parameters do not. However, these parameters can be iteratively maximized by zero-ing their gradients at:

and

See for example ^[3] and references therein. The covariance parameters are non-identifiable in the sense that for any scale factor, s>0, we have:

Drawing values from the distribution[edit]

Sampling from the matrix normal distribution is a special case of the sampling procedure for the multivariate normal distribution. Let be an n by p matrix of np independent samples from the standard normal distribution, so that

Then let

so that

where A and B can be chosen by Cholesky decomposition or a similar matrix square root operation.

Relation to other distributions[edit]

Dawid (1981) provides a discussion of the relation of the matrix-valued normal distribution to other distributions, including the Wishart distribution, inverse-Wishart distribution and matrix t-distribution, but uses different notation from that employed here.

See also[edit]

• Multivariate normal distribution

References[edit]

• Dawid, A.P. (1981). «Some matrix-variate distribution theory: Notational considerations and a Bayesian application». Biometrika. 68 (1): 265–274. doi:10.1093/biomet/68.1.265. JSTOR 2335827. MR 0614963.
• Dutilleul, P (1999). «The MLE algorithm for the matrix normal distribution». Journal of Statistical Computation and Simulation. 64 (2): 105–123. doi:10.1080/00949659908811970.
• Arnold, S.F. (1981), The theory of linear models and multivariate analysis, New York: John Wiley & Sons, ISBN 0471050652

Двумерной называют случайную величину (X,Y), возможные значения которой есть пары чисел (x,y). Составляющие X и Y, рассматриваемые одновременно, образуют систему двух случайных величин.

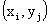
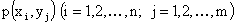
Законом распределения дискретной двумерной случайной величины называют перечень возможных значений этой величины, то есть пар чисел и их вероятностей . Обычно закон распределения задают в виде таблицы, называемой матрицей распределения.

Сумма вероятностей, помещенных во всех клетках таблицы, равна единице.

Из данной таблицы закон распределения составляющей СВ X.

где , .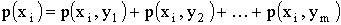

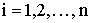
Аналогично можно найти закон распределения составляющей СВ Y.

Двумерную случайную величину (X,Y) (безразлично, дискретную или непрерывную) можно задать с помощью функции распределения F(x,y), которая определяет вероятность того, что X примет значение, меньшее x, Y — меньшее y.

.

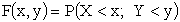
Свойства функции распределения:

1);

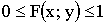
2) ;

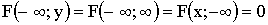
3) , где функция распределения составляющей X;

, где функция распределения составляющей Y.

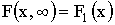
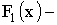
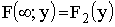
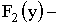
При помощи функции распределения может быть найдена вероятность

.

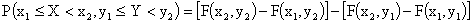
Непрерывную двумерную величину можно также задать, пользуясь плотностью распределения. Плотностью совместного распределения вероятностей f(x,y) двумерной непрерывной случайной величины (X,Y)
называют вторую смешанную частную производную от функции распределения:.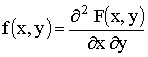

Свойства плотности распределения:

1) ;

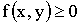
2) .

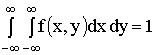
Плотности распределения

составляющей X — ;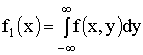

составляющей Y — .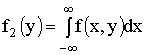

Вероятность попадания случайной точки (X,Y) в область D определяется по формуле

.

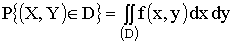
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ПРИМЕР 13.2.49. Два стрелка, независимо друг от друга, делают по одному выстрелу каждый. Случайная величина X — число попаданий первого стрелка, Y — число попаданий второго стрелка. Вероятность попадания при выстреле для первого стрелка 0,7; для второго стрелка — 0,4. Построить матрицу распределения системы случайных величин (X,Y) и законы распределения составляющих X и Y. Найти функцию распределения F(x,y).

Решение. Занесем возможные значения случайных величин X и Y в таблицу

,

,

,

.

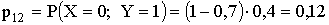
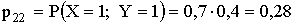
Итак,

Напишем закон распределения составляющей

,

.

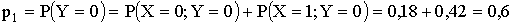
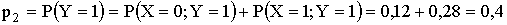
Тогда

Аналогично находится закон распределения составляющей x (складываются вероятности по столбцам).

Значения функции распределения F(x,y) находим на основании матрицы распределения

Окончательно,

ПРИМЕР 13.2.50. Задана двумерная плотность вероятности 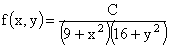системы (X,Y) двух случайных величин. Найти постоянную C и плотности распределения составляющих системы.

Решение. Воспользуемся свойством .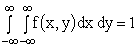

Тогда, .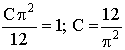

Найдем плотность распределения 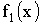составляющей X

Аналогично можно найти плотность распределения 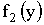составляющей Y.

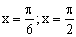
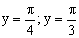
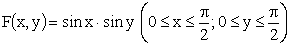
ПРИМЕР 13.2.51. Найти вероятность попадания случайной точки (X,Y) в прямоугольник, ограниченный прямыми , , если известна функция распределения

.

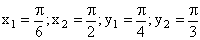
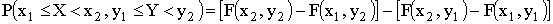
Решение. Положив в формуле

,

получим

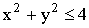
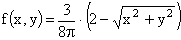
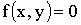
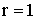
ПРИМЕР 13.2.52 В круге двумерная плотность вероятности ; вне круга . Найти вероятность попадания случайной точки (x,y) в круг радиуса с центром в начале координат.

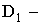
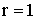
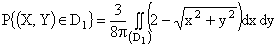
Решение: Пусть область круг радиуса с центром в начале координат, тогда

.

Перейдем к полярным координатам:

.

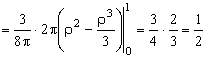
Примеры и задачи для самостоятельного решения

Решить задачи, используя формулы расчета вероятности для системы двух случайных величин

3.2.11.1. Два игрока, независимо друг от друга, по два раза выбрасывают игральный кубик. Случайная величина X — число выпадений «шестерки» у первого игрока; Y — число выпадений «шестерки» у второго игрока. Построить матрицу распределения системы случайных величин (X,Y) и законы распределения составляющих. Найти функцию распределения F(x,y).

Отв.:

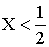
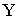
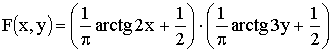
3.2.11.2. Найти вероятность того, что составляющая X двумерной случайной величины примет значение и при этом составляющая Y примет значение , если известна функция распределения системы .

Отв.:

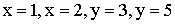
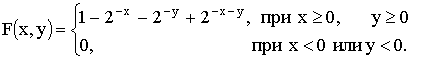
3.2.11.3. Найти вероятность попадания случайной точки (X,Y) в прямоугольник, ограниченный прямыми , если известна функция распределения .

Отв.:

3.2.11.4. Найти плотность распределения системы двух случайных величин по известной функции распределения
.

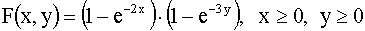
Отв.:

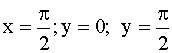
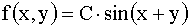
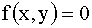
3.2.11.5. Внутри прямоугольника, ограниченного прямыми , плотность распределения системы двух случайных величин ; вне прямоугольника . Найти: а) величину C; б) функцию распределения системы F(x,y).

Отв.:

3.2.11.6. Задана двумерная плотность вероятности 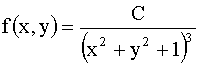системы случайных величин (X,Y). Найти постоянную C.

Указание: Перейти к полярным координатам.

Отв.:

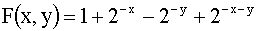
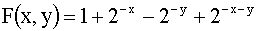
3.2.11.7. В первом квадранте задана функция распределения системы двух случайных величин: . Найти: а)двумерную плотность распределения системы; б)вероятность попадания случайной точки (X,Y) в треугольник с вершинами .

Отв.:

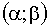
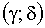
3.2.11.8. Непрерывная двумерная случайная величина (X,Y) распределена равномерно внутри прямоугольника R, ограниченного абсциссами и ординатами . Найти: а)двумерную плотность вероятности системы; б)плотности распределения составляющих. Определить, зависимы или независимы случайные величины X и Y.

Отв.:

.

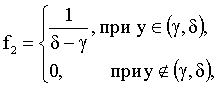
X и Y независимы,т.к. .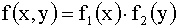

3.2.11.9. Точка (X,Y), изображающая объект на круглом экране радиолокатора, распределена с постоянной плотностью в пределах круга K радиуса r с центром в начале координат. Записать выражение совместной плотности f(x,y). Найти плотности отдельных величин, входящих в систему . Найти вероятность того, что расстояние от точки (X,Y) до центра экрана будет меньше .

Отв.:

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >