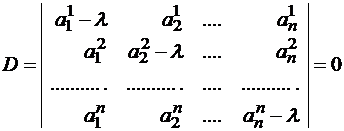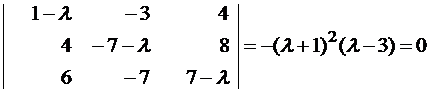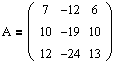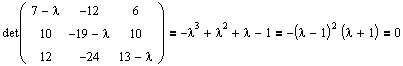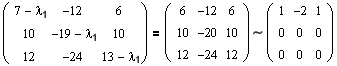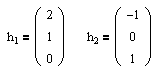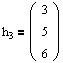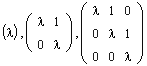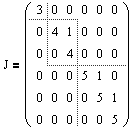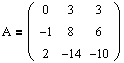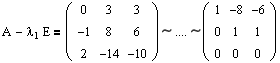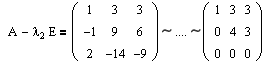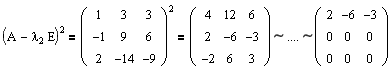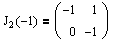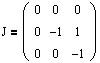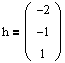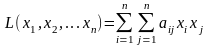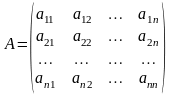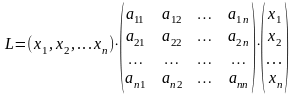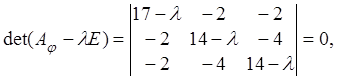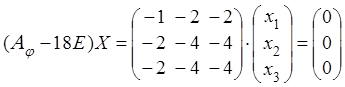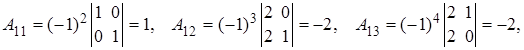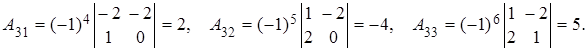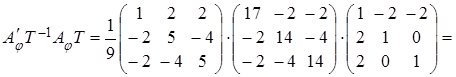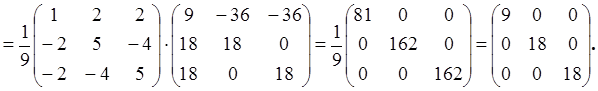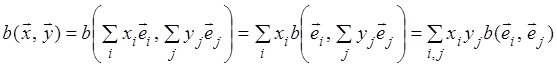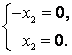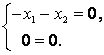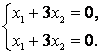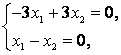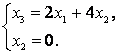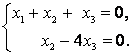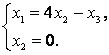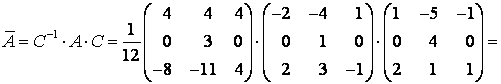Как найти матрицу в базисе собственных векторов

Собственные числа и собственные векторы линейного оператора

Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x ₁, x ₂, . x _m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x ₁, x ₂, . x _m оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_m линейно независимы.
3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется n линейно независимых собственных векторов x ₁, x ₂, . x _n, соответствующих различным собственным числам λ₁, λ₂, …, λ_n, то они линейно независимы, следовательно, их можно принять за базис пространства R_n. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 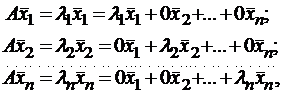тогда .
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора A в базисе < ε _i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.

Правило отыскания собственных чисел и собственных векторов

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Пример №1 . Линейный оператор A действует в R₃ по закону A· x =(x₁-3x₂+4x₃, 4x₁-7x₂+8x₃, 6x₁-7x₂+7x₃), где x₁, x₂, . x_n — координаты вектора x в базисе e ₁=(1,0,0), e ₂=(0,1,0), e ₃=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e ₁=(1,4,6)
A· e ₂=(-3,-7,-7)
A· e ₃=(4,8,7)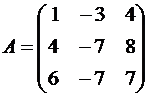
.
Составляем систему для определения координат собственных векторов:
(1-λ)x₁-3x₂+4x₃=0
x₁-(7+λ)x₂+8x₃=0
x₁-7x₂+(7-λ)x₃=0
Составляем характеристическое уравнение и решаем его:

Пример №2 . Дана матрица .
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.

Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x — собственный вектор

Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой a_i k =a_k i .

Замечания .

1. Все собственные числа симметрической матрицы вещественны.
2. Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.

В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

Собственные векторы матрицы

Онлайн калькулятор нахождение собственных чисел и собственных векторов — Собственный вектор — понятие в линейной алгебре, определяемое для квадратной матрицы или произвольного линейного преобразования как вектор, умножение матрицы на который или применение к которому преобразования даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение, называемое собственным числом матрицы или линейного преобразования.

Данный калькулятор поможет найти собственные числа и векторы, используя характеристическое уравнение.

Алгоритм нахождения векторов жорданова базиса

Собственные векторы и собственные значения

Пусть A – матрица некоторого линейного преобразования порядка n.

Определение. Многочлен n-ой степени

P(l)=det(A-lЕ) (1.1)

называется характеристическим многочленом матрицы А, а его корни, которые могут быть как действительными, так и комплексными, называются характеристическими корнями этой матрицы.

Определение. Ненулевой вектор x линейного пространства V, удовлетворяющий условию

А(х)=lх, (1.2)

называется собственным вектором преобразования A. Число l называется собственным значением.

Замечание. Если в пространстве V задан базис, то это условие можно переписать следующим образом:

Ах=lх, (1.3)

где A – матрица преобразования, x – координатный столбец.

Определение. Алгебраической кратностью собственного значения l_j называется кратность корня l_j характеристического многочлена.

Определение. Совокупность всех собственных значений называется спектром матрицы.

Алгоритм нахождения собственных значений и собственных векторов

1. Найти собственные значения матрицы:

· записать характеристическое уравнение:

det(A-lЕ)=0; (1.4)

· найти его корни l _j, j=1. n и их кратности.

2. Найти собственные векторы матрицы:

· для каждого l _j решить уравнение

· найденный вектор х и будет собственным вектором, отвечающим собственному значению l _j.

Пример1

Найдем собственные значения и собственные векторы, если известна матрица преобразования:

Записываем характеристический многочлен (1.1) и решаем характеристическое уравнение (1.4):

Получаем два собственных значения: l₁=1 кратности m₁=2 и l₂=-1 кратности m₂=1.

Далее с помощью соотношения (1.5) находим собственные векторы. Сначала ищем ФСР для l₁=1:

Очевидно, что rang=1, следовательно, число собственных векторов для l₁=1 равно n-rang=2. Найдем их:

Аналогичным образом находим собственные векторы для l₂=-1. В данном случае будет один вектор:

Понятие жордановой клетки и жордановой матрицы

Определение. Жордановой клеткой порядка m, отвечающей собственному значению l, называется матрица вида:

(2.1)

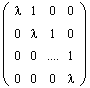
Иными словами, на главной диагонали такой матрицы располагается собственное значение l, диагональ, ближайшая к главной, сплошь занята единицами, а все остальные элементы матрицы равны нулю. Ниже даны примеры жордановых клеток соответственно первого, второго и третьего порядков:

Определение. Блочно-диагональная матрица, на диагонали которой стоят жордановы клетки, называется жордановой матрицей:

(2.2)

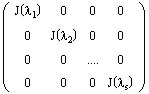
Пример

Ниже представлена жорданова матрица, состоящая из трех жордановых клеток:

— размера 1, отвечающая собственному значению l₁=3;

— размера 2, отвечающая собственному значению l₂=4;

— размера 3, отвечающая собственному значению l₃=5.

Количество и размер жордановых клеток

Пусть А — матрица, которую нужно привести к жордановой форме, l_j (k=1. m_j) — собственные значения этой матрицы.

Количество жордановых клеток размера k, отвечающих собственному значению l_j, определяется следующим образом:

(3.1)
(3.2)

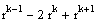
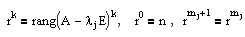
Пример

Пусть дана матрица преобразования:

Найдем количество и размер жордановых клеток, соответствующих каждому собственному значению этого преобразования.

Как искать собственные значения, было подробно рассказано в первом параграфе учебника. Поэтому опустим все расчеты, а сразу укажем собственные числа матрицы А: l₁=0 кратности m₁=1 и l₂=-1 кратности m₂=2.

Используя соотношения (3.1) и (3.2), найдем количество и размер жордановых клеток, соответствующих l₁=0, m₁=1.

Очевидно, что rang(A-l₁E)=2 и, соответственно, r 1 =r 2 =rang(A-l₁E) 1 =2, r 0 =n=3.

Количество жордановых клеток размера 1 будет равно: r 0 -2r 1 +r 2 =3-2*2+2=1.

Ясно, что других клеток для этого собственного значения нет. Т.о., для l₁=0, m₁=1 мы имеем единственную жорданову клетку вида J₁(0)=(0).

Далее аналогичным образом определяем клетки для второго собственного значения l₂=-1 кратности m₂=2.

Очевидно, что rang(A-l₂E)=2 и, соответственно, r 1 =r 2 =rang(A-l₂E) 1 =2.

Т.е. rang(A-l₁E) 2 =1 и, соответственно, r 1 =r 2 =rang(A-l₁E) 2 =1.

Теперь можно определить количество и размер жордановых клеток для второго собственного значения:

— размера 1: r 0 -2r 1 +r 2 =3-2*2+1=0;

— размера 2: r 1 -2r 2 +r 3 =2-2*1+1=1.

Таким образом, для l₂=-1 мы получили одну клетку размера 2:

Соответственно, жорданова форма для исходной матрицы А будет иметь вид:

Жорданов базис

Пусть матрица А приведена к жордановой форме J. Рассмотрим систему HJ=AH, где

— матрица перехода от исходного базиса (e) к жорданову базису (h). Это система матричных n 2 уравнений с n 2 неизвестными.

Определение. Пусть e – собственный вектор преобразования А, т.е. имеет место равенство А(e) = le. Вектор e1, удовлетворяющий равенству

называется присоединенным вектором первого порядка;

вектор e₂, удовлетворяющий равенству

— присоединенным вектором второго порядка;

вектор e_n, удовлетворяющий равенству

— присоединенным вектором n-ого порядка.

Заметим также, что

(А-lе) k e_k=e. (4.5)

Алгоритм нахождения векторов жорданова базиса

Чтобы найти жорданов базис, необходимо проделать следующие действия для каждой жордановой клетки.

Рассмотрим жорданову клетку порядка k, отвечающую собственному значению l. Для нее ищутся вектора жорданова базиса:

h, h 1 , h 2 , . h k-1 , где:

h — собственный вектор, отвечающий собственному значению l;

h 1 — присоединенный вектор 1-ого порядка;

h 2 — присоединенный вектор 2-ого порядка;

h k-1 — присоединенный вектор (k-1)-ого порядка;

Эта совокупность векторов ищется, используя следующую систему:

(4.6)

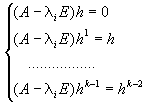
В результате применения этих операций ко всем жордановым клеткам, получим векторы, составляющие жорданов базис:

h, h 1 , h 2 , . h k-1 , f, f 1 , f 2 , . f p-1 .

Векторам h соответствует жорданова клетка размера k, векторам f – размера p и т.д.
ex3

Пример

Вернемся к примеру, рассмотренному в прошлом разделе. Там нами были получены две жордановы клетки:

J₁(0)=(0) и

Рассмотрим первую, J₁(0).

С помощью соотношения (1.5) из первого параграфа найдем собственный вектор, отвечающий собственному значению l₁=0:

Присоединенных векторов для данной жордановой клетки, очевидно, нет.

Теперь рассмотрим вторую жорданову клетку, J₂(-1). Очевидно, что для нее надо найти один собственный вектор и один присоединенный.

Используя систему (4.6), получим эти векторы:

— собственный вектор, отвечающий l₂=-1;

— присоединенный вектор.

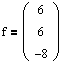
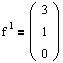
Мы получили все векторы, составляющие матрицу Н. Таким образом, матрица перехода к жорданову базису будет иметь следующий вид:

Матрица
A
линейного оператора A
пространства Rⁿ
в себя принимает наиболее простой вид,
если базис пространства состоит из
собственных векторов оператора A.

Можно
доказать, что в этом случае матрица A
линейного оператора является диагональной
и имеет вид:

.

Верно
и обратное: если матрица A
линейного оператора A
в некотором базисе является диагональной,
то все векторы этого базиса являются
собственными векторами оператора A.

23. Квадратичная форма (определение). Матрица квадратичной формы. Ранг квадратичной формы

Определение 1. Квадратичной
формой L(x₁, x₂, … , x_n)
от n
переменных называется сумма, каждый
член которой является либо квадратом
одной из переменных, либо произведением
двух разных переменных x_ix_j,
взятых с некоторым действительным
коэффициентом a_ij,
(причем a_ij = a_ji):

.

Определение 2. Матрицей
квадратичной формы L(x₁, x₂, … , x_n)
от n
переменных называется матрица,
составленная из коэффициентов a_ij:

.

Отметим,
что в силу условия a_ij = a_ji,
она является симметрической.

Ее диагональные
элементы равны коэффициентам при
квадратах переменных.

Определение 3. Матричной
записью квадратичной формы L(x₁, x₂, … , x_n)
от n
переменных называется запись L=XAX,
где X=(x₁, x₂, … , x_n)
— матрица столбец переменных.

Следовательно,

.

Определение 2. Рангом
квадратичной формы L(x₁, x₂, … , x_n)
от n
переменных называется ранг матрицы
квадратичной формы.

24. Квадратичная форма (канонический вид). Приведение квадратичной формы к каноническому виду. Закон инерции квадратичных форм

Определение 1. Квадратичная
форма
L(x₁, x₂, … , x_n)
от n
переменных называется канонической,
если все её коэффициенты при произведениях
различных переменных равны нулю, т.е.
a_ij=0
при ij.

В
этом случае квадратичная форма имеет
вид

.

Доказано,
что любая квадратичная форма с помощью
линейного невырожденного преобразования
может быть приведена к каноническому
виду.

При
этом её матрица приводится к диагональному
виду.

Теорема
1 (закон инерции квадратичных форм). Ранг
квадратичной формы не меняется при
линейных преобразованиях.

Следовательно,
ранг квадратичной формы
L(x₁, x₂, … , x_n)
от n
переменных равен числу отличных от
нуля коэффициентов канонической формы
и совпадает с рангом соответствующей
диагональной матрицы.

26. Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости (одно из них вывести)

Определение 1. Уравнением
линии на плоскости
Oxy
называется уравнение F(x,y)=0,
которому удовлетворяют координаты x
и y
каждой точки линии и только они.

Если
из этого уравнения выразить переменную
y,
то получится уравнение y=f(x).

Если
линии заданы уравнениями, то точкой
пересечения двух линий
называется любая точка, координаты x
и y
которой удовлетворяют уравнениям, т.е.
являются решением системы двух уравнений.

Основные
виды уравнений прямой на плоскости:

1) у=0
— уравнение оси Ох;
y=b
— уравнение прямой, параллельной оси
Ох;

2) х=0
— уравнение оси Оу;
х=а
— уравнение прямой, параллельной оси
Оу;

3) y=kх
— уравнение прямой, проходящей через
начало координат, с угловым коэффициентом
k=tg,
где -
угол наклона прямой к оси Oх;

4) y=kх+b
— уравнение
прямой с угловым коэффициентом
k=tg,
где -
угол наклона прямой с положительным
направлением оси Oх.

y—y₀=k(x—x₀)
— уравнение
прямой, проходящей через точку
(x₀,y₀)
и имеющей
угловой коэффициент
k.

— уравнение
прямой, проходящей через две данные
точки (x₁,y₁)
и (x₂,y₂)
, если x₁x₂
и y₁y₂.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

, , следовательно, , так как  –
произвольные векторы, то , следовательно, по
определению  – ортогональная матрица и .

Пример 6.1. Пусть
линейный оператор , действующий в
евклидовом пространстве,
имеет в ортонормированном базисе матрицу . Построить в этом пространстве
базис из собственных векторов оператора  и найти матрицу оператора  в этом базисе.

.

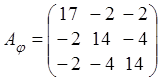
Решение.
1) Найдем собственные числа оператора , для
чего составим и решим характеристическое уравнение (4.3):

Приравняв
к нулю, находим:

2)
Находим собственные векторы, соответствующие найденным собственным значениям,
для чего при каждом  составляем и решаем систему
(4.2): а)
при , получаем

что равносильно системе (здесь )

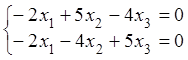
  , полагая в которой, например, , находим , таким образом, собственный вектор,
соответствующий собственному значению 9, есть

б)
при , получаем

что равносильно
уравнению (здесь )

, полагая в котором
сначала , а затем ,
получаем еще два линейно независимых собственных вектора:

.

3)
Находим матрицу перехода к базису из собственных векторов и обратную к ней
(столбцами матрицы перехода являются координатные столбцы векторов  (см.
раздел 1)):

 .

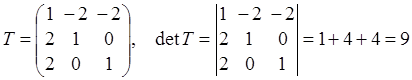
4)
Теперь по формуле (4.1) находим  – матрицу
линейного оператора в базисе из собственных векторов

Таким
образом, матрица линейного оператора в базисе из собственных векторов диагональная!

7. БИЛИНЕЙНЫЕ
И КВАДРАТИЧНЫЕ ФОРМЫ

7.1.
Билинейные формы

Определение.
Отображение  называется числовой функцией, т.е.
числовая функция – закон или правило, по которому каждому вектору  (каждой паре векторов ) ставится в соответствие число из R.

Определение.
Числовая функция  называется линейной формой,если  и  справедливо:

a) 

b) 

Определение.
Числовая функция двух аргументов – закон или правило, по которому каждой паре
векторов  ставится в
соответствие число из .

Определение.
Числовая функция , аргументами которой
являются всевозможные векторы , называется билинейной
формой, если  и  выполняются соотношения:

а)

б)

в)

г)

т.е. функция является линейной по каждому из аргументов, где условия а),
в) означают линейность по первому аргументу; условия б), г) – по
второму.

Выберем какой — либо базис  в . Тогда

  

и значение билинейной формы может
быть вычислено следующим образом

или

                                   (7.1)

где  (i, j = l, 2, …, n)
– значения билинейной формы на всевозможных парах базисных векторов,
которые называются коэффициентами билинейной формы в базисе е.

Коэффициенты  образуют квадратную матрицу порядка п

, которая называется матрицей
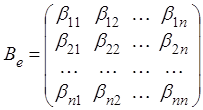
билинейной формы в данном базисе е. Как легко проверить, в матричном
виде равенство (7.1) имеет вид

(7.2)

Теорема
7.1. Любая квадратная матрица  в некотором базисе
является матрицей билинейной формы.

Доказательство.
Определим  с базисом  с помощью матрицы  числовую
функцию  по правилу

.

Легко проверяются свойства
(7.1). Но тогда элементы  равны , где , и
записанная формула есть определение билинейной формы (7.2).

Согласно
теореме 7.1., естественно называть представление (7.2.) общим видом билинейной
формы в n-мерном линейном Евклидовом пространстве .

Определение.
Билинейная форма  называется симметричной
(кососимметричной), если  выполняется равенство

        
.

Теорема
7.2. Билинейная форма является симметричной (кососимметричной) тогда и
только тогда, когда ее матрица симметрическая, т.е.  или  (кососимметрическая, т.е.  или ).

Доказательство. 
 Так как форма симметрична, то :

.

В
частности, для базисных векторов , следовательно, . Аналогично для кососимметричной формы.

 Пусть матрица билинейной формы
симметрическая, т.е. . Тогда, так как матрица размеров
 не меняется при транспонировании:

.

Теорема
7.3. Матрицы  и  билинейной
формы  в базисах e и  связаны соотношением

                                                   
(7.3)

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.

Доброго времени суток, форумчане!
Как найти матрицу оператора в базисе из собственных и присоединенных векторов? По формуле B=S[math]^{-1}[/math] * A * S? Где В — нужная матрица, S[math]^{-1}[/math] — обратная матрицы перехода, S — матрица перехода, А — заданная матрица.
И еще: как повлияет то, что собственный и присоединенный вектор равны между собой, на матрицу перехода?
Данные в качестве примера: А = [math]begin{pmatrix} 136 & -16 \ 4 & 152 end{pmatrix}[/math] , [math]lambda = 144[/math] (кратности 2), а собственный и присоединенный вектора равны [math]begin{pmatrix} -2 \ 1 end{pmatrix}[/math]

Задание 1. Линейный оператор преобразует векторы , , в векторы , , . Найти матрицу линейного оператора.

Решение. Матрицы

, и

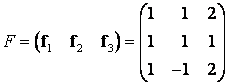
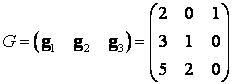
Связаны между собой соотношением , откуда .

Так как , то , а искомая матрица линейного оператора .

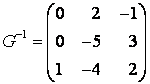
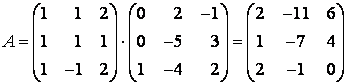
Ответ: .

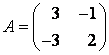
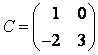
Задание 2. Пусть линейный оператор в базисе задан матрицей . Найти матрицу этого линейного оператора в базисе , если матрица является матрицей перехода от базиса к базису .

Решение. Матрицы и линейного оператора , заданного в разных базисах, связаны между собой соотношением . Так как , то

.

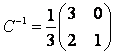
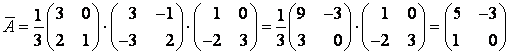
Ответ: .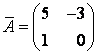

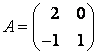
Задание 3. Линейный оператор в базисе задан матрицей . Найти матрицу этого линейного оператора в базисе , если , .

Решение. Связь между матрицами и линейного оператора в разных базисах определяется формулой , где – матрица перехода от базиса к базису .

Составим матрицу : , тогда и, следовательно,

.

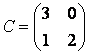
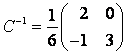
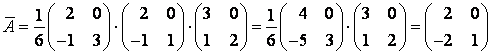
Ответ: .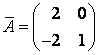

Задание 4. Линейный оператор в базисе задан матрицей . Найти матрицу этого линейного оператора в базисе , если , .

Решение. Матрицы и связаны между собой соотношением , где – матрица перехода от базиса к базису .

Составим матрицу : , тогда и, следовательно,

Ответ: .

Задание 5. Найти собственные значения и собственные векторы линейного оператора , заданного в некотором базисе матрицей .

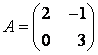
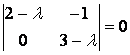
Решение. Для нахождения собственных значений линейного оператора составим характеристическое уравнение , т. е. . Раскрывая определитель, получим , т. е. , .

По определению называется собственным вектором линейного оператора , соответствующим собственному значению , если .

Найдём собственные векторы и , соответствующие собственным значениям и .

При получим: , что равносильно такой однородной системе уравнений:

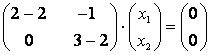
Если – базисная переменная, а – свободная, то .

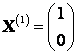
При : , что равносильно однородной системе уравнений

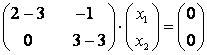
Пусть – базисная переменная, – свободная. Примем , тогда , а следовательно, .

Так как собственные векторы соответствуют различным собственным значениям, то они должны быть линейно независимы. Проверим линейную независимость полученных собственных векторов и .

Составим матрицу . Так как , то собственные векторы и линейно независимы.

Ответ: собственные числа , ; собственные векторы , .

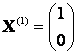
Задание 6. Привести матрицу 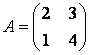линейного оператора к диагональному виду.

Решение. Матрица линейного оператора будет диагональной в базисе из собственных векторов, если такой базис существует. Найдём собственные значения и собственные векторы линейного оператора.

Запишем характеристическое уравнение: 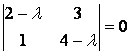, т. е. или , откуда получаем , .

Найдём собственные векторы И .

При получим: , что соответствует следующей однородной системе уравнений:

Пусть – базисная переменная, – свободная. Полагая , получим .

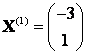
При : . Соответствующая однородная система уравнений имеет вид:

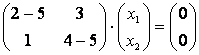
Откуда . Пусть – базисная переменная, – свободная, примем тогда , а, следовательно, .

Собственные векторы и отвечают различным собственным значениям, поэтому они линейно независимы, т. е. могут составить базис. Матрица линейного оператора в базисе из собственных векторов и имеет диагональный вид: .

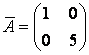
Можно проверить полученный результат. Так как , где матрица в случае перехода к базису из собственных векторов и имеет вид , следовательно,

,

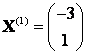
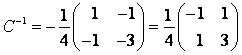
Тогда

.

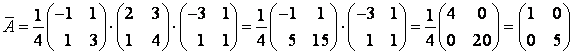
Ответ: .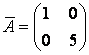

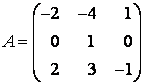
Задание 7. Найти собственные значения и собственные векторы линейного оператора , заданного в некотором базисе матрицей . Построить, если это возможно, базис из собственных векторов и найти матрицу этого линейного оператора в базисе из собственных векторов.

Решение. Запишем характеристическое уравнение:

,

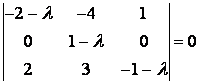
Т. е. ,

, откуда получаем , , .

Найдём собственные векторы линейного оператора.

При : , тогда соответствующая однородная система уравнений примет вид:

или

Что равносильно такой системе:

Пусть и – базисные переменные, – свободная. Полагая , получим .

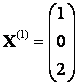
При : , или, переходя к однородной системе уравнений, получим

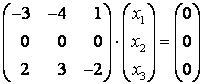
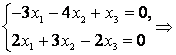
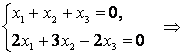
Пусть и – базисные переменные, – свободная. Если , то .

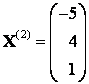
При получим: , и однородная система уравнений примет вид:

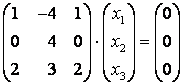
Пусть и – базисные переменные, – свободная. Тогда если , то . Найденные собственные векторы соответствуют различным собственным значениям, поэтому они линейно независимы, значит, существует базис из собственных векторов. Матрица перехода к такому базису , тогда

.

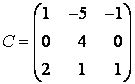
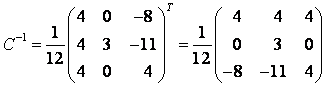
Матрица линейного оператора в базисе из собственных векторов имеет вид: .

Можно сделать проверку полученных результатов:

.

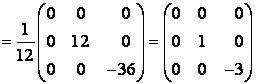
Ответ: , , ; , , ; матрица линейного оператора в базисе из собственных векторов .

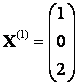
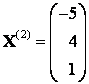
< Предыдущая		Следующая >