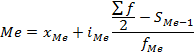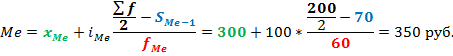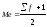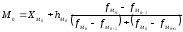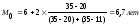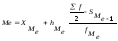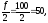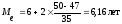Представим такую ситуацию: мы опросили 10 человек на предмет их уровня доходов. У 9-х доходы оказались примерно одинаковыми и составили 10 тыс. руб. Что касается 10-ого опрошенного, то оказалось, что его доход равняется 410 тыс. руб. в месяц. Если мы вычислим простое среднее арифметическое, то типичный доход будет равняться 50 тыс. руб.! Но это явно не так. В таких ситуациях более объективную и правдоподобную картину дает вычисление моды или медианы, которые относятся к структурным средним показателям.
Понятие медианы
Медиана (Me) — значение признака в исследуемом ряду величин, которое делит этот ряд на две равные части.
То есть половина (50%) всех значений в исследуемом ряду будет меньше медианы, а другая половина — больше ее. Поэтому медиану еще называют 50-й перцентиль или квантиль 0,5.
Формула для расчета медианы
Если значений немного, то медиану можно определить «на глазок». Для этого достаточно расположить все значения в порядке возрастания и найти середину.
Если число случаев четное и в центре ряда находятся два разных числа, то медианой будет среднее между ними (даже если такого значения нет в самом ряду исследуемых случаев). Например, в ряду 1 2 3 4 5 6, медианой будет 3,5.
Для нахождения медианы в более сложных случаях (по интервальным рядам) используется специальная формула:
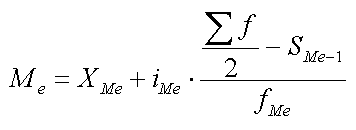
где: Me — медиана;
Xme — нижняя граница медианного интервала (того интервала, накопленная частота которого превышает полусумму всех частот);
ime — величина медианного интервала;
f — частота (сколько раз в ряду встречается то или иное значение);
Sme-1 — сумма частот интервалов предшествующих медианному интервалу;
fme — число значений в медианном интервале (его частота).
Пример вычисления медианы
Был проведен опрос среди покупателей с целью выяснить их типичный возраст. По результатам опроса было установлено, что: 25 покупателей имеют возраст до 20 лет; 32 покупателя — 20-40 лет; 18 покупателей — 40-60 лет; 15 покупателей — свыше 60 лет. Найдем медиану.
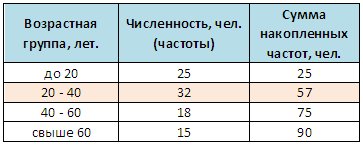
Сначала находим медианный интервал. Для этого вычисляем сумму частот: 25 + 32 + 18 + 15 = 90. Половина этой суммы — 45. Это соответствует возрастной группе 20-40 лет (т. к. полученная полусумма частот — 45, и накопленная частота 1-й группы меньше ее, а 3-ей — больше). Тогда нижняя граница медианного интервала — 20 (лет), а величина медианного интервала — 20 (40 лет за вычетом 20). Сумма частот интервалов предшествующих медианному интервалу — 25. Число значений в медианном интервале — 32 (количество покупателей в возрасте 20-40 лет).
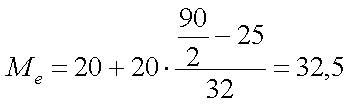
Расчетное значение медианы — 32,5. Округив его, получим средний возраст покупателя — 33 года.
Область применения медианы
При вычислении типичного признака неоднородных рядов, имеющих «выбросы» — значения во много раз отличающиеся от других значений ряда.
Особенности медианы
- Медиана обладает высокой робастностью, то есть нечувствительностью к неоднородностям и ошибкам выборки;
- Сумма разностей между членами ряда выборки и медианой меньше, чем сумма этих разностей с любой другой величиной. В том числе с арифметическим средним.
Источники
- Медиана // Википедия. URL: http://ru.wikipedia.org/wiki/Медиана_(статистика) (дата обращения: 23.10.2013)
- Минашкин В. Г. и др. Курс лекций по теории статистики. – М.: МЭСИ, 2001.
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Нашли опечатку? Помогите сделать статью лучше! Выделите орфографическую ошибку мышью и нажмите Ctrl + Enter.
Библиографическая запись для цитирования статьи по ГОСТ Р 7.0.5-2008:
Галяутдинов Р.Р. Медиана // Сайт преподавателя экономики. [2013]. URL: https://galyautdinov.ru/post/mediana (дата обращения: 28.05.2023).
Формула для расчета медианы в статистике
Медианная формула в статистике относится к формуле, используемой для определения среднего числа в заданном наборе данных, расположенном в порядке возрастания. Согласно подсчету формулы количество элементов в наборе данных добавляется к единице. Таким образом, результаты будут разделены на два, чтобы получить место срединного значения, т. е. число, помещенное в идентифицированную позицию, будет средним значением.
Это инструмент для измерения центра набора числовых данных. Он суммирует большие объемы данных в одно значение. Его можно определить как среднее число группы чисел, отсортированных в порядке возрастания. Другими словами, медиана — это число, над которым и под ним будет одинаковое количество чисел в указанной группе данных. Это широко используемая мера наборов данных в статистике. В статистике статистика — это наука, стоящая за выявлением, сбором, организацией и обобщением, анализом, интерпретацией и, наконец, представлением таких данных, как качественных, так и количественных, что помогает принимать более эффективные и эффективные решения с уместностью. читать дальше и теория вероятностей.
Медиана = {(n+1)/2}-й
Где «n» — количество элементов в наборе данных, а «th» означает (n)-е число.
Оглавление
- Формула для расчета медианы в статистике
- Расчет медианы (шаг за шагом)
- Примеры формулы медианы в статистике
- Пример №1
- Пример #2
- Пример №3
- Актуальность и использование
- Медианная формула в статистике (с шаблоном Excel)
- Рекомендуемые статьи
Расчет медианы (шаг за шагом)
Выполните следующие шаги:
- Во-первых, отсортируйте числа в порядке возрастания. Числа располагаются по возрастанию при расположении от наименьшего к наибольшему порядку в этой группе.
- Метод нахождения медианы нечетных/четных чисел в группе приведен ниже.
- Если количество элементов в группе нечетное – Найдите {(n+1)/2}-й член. Значение, соответствующее этому термину, является медианой.
- Если количество элементов в группе четное — Найдите {(n+1)/2}-й член в этой группе. Средняя точка между числами по обе стороны от срединной позиции. Например, если имеется восемь наблюдений, медиана равна (8+1)/2-й позиции, то есть можно вычислить 4,5-ю медиану, добавив 4-й и 5-й члены в этой группе, которая затем делится на 2.
Примеры формулы медианы в статистике
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Excel с медианной формулой здесь – Шаблон медианной формулы Excel
Пример №1
Список чисел: 4, 10, 7, 15, 2. Вычислить медиану.
Решение: Расположим числа в порядке возрастания.
В порядке возрастания числа: 2,4,7,10,15.
Всего 5 номеров. Медиана равна (n+1)/2-му значению. Таким образом, медиана равна (5+1)/2-му значению.
Медиана = 3-е значение.
3-е значение в списке 2, 4, 710, 15 равно 7.
Таким образом, медиана равна 7.
Пример #2
Предположим, в организации 10 сотрудников, включая генерального директора. Генеральный директор Адам Смит считает, что зарплата сотрудников высока. Следовательно, он хочет оценить зарплату, получаемую группой, и, следовательно, принимать решения.
Ниже указана заработная плата сотрудников фирмы. Рассчитайте среднюю заработную плату. Заработная плата составляет 5 000 долларов, 6 000 долларов, 4 000 долларов, 7 000 долларов, 8 000 долларов, 7 500 долларов, 10 000 долларов, 12 000 долларов, 4 500 долларов, 10 00 000 долларов.
Решение:
Сначала расположим оклады в порядке возрастания. Заработная плата в порядке возрастания:
4000 долларов, 4500 долларов, 5000 долларов, 6000 долларов, 7000 долларов, 7500 долларов, 8000 долларов, 10000 долларов, 12000 долларов, 1000000 долларов
Таким образом, расчет медианы будет следующим:
Поскольку элементов 10, медиана равна (10+1)/2-му элементу. Медиана = 5,5-й пункт.
Таким образом, медиана — это среднее значение 5-го и 6-го пунктов. Например, 5-й и 6-й предметы стоят 7000 и 7500 долларов.
= (7000 долл. США + 7500 долл. США)/2 = 7250 долл. США.
Таким образом, средняя заработная плата 10 сотрудников составляет 7250 долларов.
Пример №3
Джеффу Смиту, генеральному директору производственной организации, необходимо заменить семь машин новыми. Однако он обеспокоен понесенными затратами и звонит финансовому директору фирмы, чтобы тот помог ему рассчитать медианную стоимость семи новых машин.
Финансовый менеджер предположил, что можно покупать новые машины, если средняя цена машин ниже 85 000 долларов. Затраты следующие: 75 000 долларов, 82 500 долларов, 60 000 долларов, 50 000 долларов, 1 00 000 долларов, 70 000 долларов, 90 000 долларов. Рассчитайте среднюю стоимость машин. Затраты следующие: 75 000 долларов, 82 500 долларов, 60 000 долларов, 50 000 долларов, 1 00 000 долларов, 70 000 долларов, 90 000 долларов.
Решение:
Расположите затраты в порядке возрастания: 50 000 долларов, 60 000 долларов, 70 000 долларов, 75 000 долларов, 82 500 долларов, 90 000 долларов, 1 00 000 долларов.
Таким образом, расчет медианы будет следующим:
Поскольку элементов 7, медиана равна (7+1)/2-й элемент, т. е. 4-й элемент. Следовательно, 4-й предмет стоит 75 000 долларов.
Поскольку медиана ниже 85 000 долларов, можно купить новые машины.
Актуальность и использование
Основное преимущество медианы перед средними заключается в том, что на нее не оказывают чрезмерного влияния крайние значения, которые могут быть очень высокими и очень низкими. Таким образом, это дает человеку лучшее представление о репрезентативной ценности. Например, если вес 5 человек в кг равен 50, 55, 55, 60 и 150. Среднее значение равно (50+55+55+60+150)/5 = 74 кг. Однако 74 кг не является истинным репрезентативным значением, поскольку большинство весов находится в диапазоне от 50 до 60. Вычислим медиану в таком случае. Это будет (5+1)/2-й член = 3-й член. Третий член — 55 кг, что является медианой. Поскольку большинство данных находится в диапазоне от 50 до 60, 55 кг являются истинным репрезентативным значением данных.
Мы должны быть осторожны в интерпретации того, что означает медиана. Например, когда мы говорим, что средний вес составляет 55 кг, не все люди весят 55 кг. Кто-то может весить больше, а кто-то меньше. Однако 55 кг – это хороший показатель веса 5 человек.
В реальном мире, чтобы понять наборы данных, такие как доход домохозяйства или активы домохозяйства, которые сильно различаются, среднее значение может быть искажено небольшим количеством очень больших значений или малых значений. Таким образом, медиана используется, чтобы предположить, каким должно быть типичное значение.
Медианная формула в статистике (с шаблоном Excel)
Билл — владелец обувного магазина. Он хочет знать, какой размер обуви ему следует заказать. Он спрашивает 9 покупателей, какой у них размер обуви. Результатами являются 7, 6, 8, 8, 10, 6, 7, 9 и 6. Вычислите медиану, чтобы помочь Биллу принять решение о заказе.
Решение: Сначала мы должны расположить размеры обуви в порядке возрастания.
Это: 6, 6, 6, 7, 7, 8, 8, 9, 10
Ниже приведены данные для расчета медианы обувного магазина.
Поэтому вычисление медианы в excelMedian In ExcelMEDIAN в Excel дает медиану заданного набора чисел. МЕДИАНА Определяет положение центра группы чисел в статистическом распределении. Подробнее будет следующим:
В Excel можно использовать встроенную формулу для медианы, чтобы вычислить медиану группы чисел. Выберите пустую ячейку и введите это = МЕДИАНА (B2: B10) (B2: B10 указывает диапазон, из которого вы хотите вычислить медиану).
Медиана обувного магазина будет –
Рекомендуемые статьи
Эта статья была руководством по медианной формуле в статистике. Здесь мы обсуждаем расчет медианы с использованием ее формулы и практических примеров в Excel и загружаемого шаблона Excel. Вы можете узнать больше об Excel из следующих статей: –
- ФормулаФормулаНормальное распределение – это симметричное распределение, т.е. положительные и отрицательные значения распределения можно разделить на равные половины, и поэтому среднее значение, медиана и мода будут равны. У него два хвоста, один известен как правый хвост, а другой известен как левый хвост. Узнайте больше о нормальном распределении нормального распределения. на равные половины и, следовательно, среднее значение, медиана и мода будут равны. У него два хвоста, один известен как правый хвост, а другой известен как левый хвост.Подробнее
- Вычислить стандартное нормальное распределениеВычислить стандартное нормальное распределениеСтандартное нормальное распределение — это симметричное распределение вероятностей относительно среднего или среднего значения, показывающее, что данные, близкие к среднему или среднему, встречаются чаще, чем данные, далекие от среднего или нормы. Таким образом, оценка называется «Z-оценка».Подробнее
- Формула МЕДИАНА в ExcelФормула МЕДИАНА в Excel Функция МЕДИАНА в Excel дает медиану заданного набора чисел. МЕДИАНА Определяет расположение центра группы чисел в статистическом распределении.Подробнее
- Вычислить среднее значение населенияВычислить среднее значение населенияСреднее значение населения представляет собой среднее значение всех значений в данной совокупности и рассчитывается как сумма всех значений в совокупности, обозначаемая суммой X, деленная на количество значений в совокупности, которое обозначается N. читать далее
Центральную тенденцию данных можно рассматривать не только, как значение с нулевым суммарным отклонением (среднее арифметическое) или максимальную частоту (мода), но и как некоторую отметку (значение в совокупности), делящую ранжированные данные (отсортированные по возрастанию или убыванию) на две равные части. Половина исходных данных меньше этой отметки, а половина – больше. Это и есть медиана.
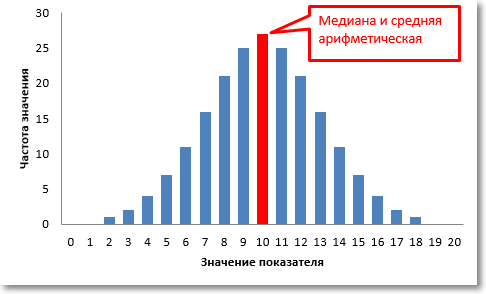
Итак, медиана в статистике – это уровень показателя, который делит набор данных на две равные половины. Значения в одной половине меньше, а в другой больше медианы. В качестве примера обратимся к набору нормально распределенных случайных чисел.
Очевидно, что при симметричном распределении середина, делящая совокупность пополам, будет находиться в самом центре – там же, где средняя арифметическая (и мода). Это, так сказать, идеальная ситуация, когда мода, медиана и средняя арифметическая совпадают и все их свойства приходятся на одну точку – максимальная частота, деление пополам, нулевая сумма отклонений – все в одном месте. Однако, жизнь не так симметрична, как нормальное распределение.
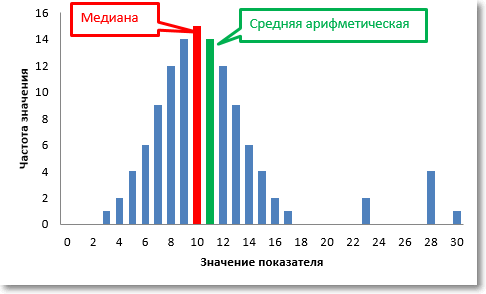
Допустим, мы имеем дело с техническими замерами отклонений от ожидаемой величины чего-нибудь (содержания элементов, расстояния, уровня, массы и т.д. и т.п.). Если все ОК, то отклонения, скорее всего, будут распределены по закону, близкому к нормальному, примерно, как на рисунке выше. Но если в процессе присутствует важный и неконтролируемый фактор, то могут появиться аномальные значения, которые в значительной мере повлияют на среднюю арифметическую, но при этом почти не затронут медиану.
Медиана выборки – это альтернатива средней арифметической, т.к. она устойчива к аномальным отклонениям (выбросам).
Математическим свойством медианы является то, что сумма абсолютных (по модулю) отклонений от медианного значения дает минимально возможное значение, если сравнивать с отклонениями от любой другой величины. Даже меньше, чем от средней арифметической, о как! Данный факт находит свое применение, например, при решении транспортных задач, когда нужно рассчитать место строительства объектов около дороги таким образом, чтобы суммарная длина рейсов до него из разных мест была минимальной (остановки, заправки, склады и т.д. и т.п.).
Формула медианы
Формула медианы в статистике для дискретных данных чем-то напоминает формулу моды. А именно тем, что формулы как таковой нет. Медианное значение выбирают из имеющихся данных и только, если это невозможно, проводят несложный расчет.
Первым делом данные ранжируют (сортируют по убыванию). Далее есть два варианта. Если количество значений нечетно, то медиана будет соответствовать центральному значению ряда, номер которого можно определить по формуле:
где
№Me – номер значения, соответствующего медиане,
N – количество значений в совокупности данных.
Тогда медиана обозначается, как
Это первый вариант, когда в данных есть одно центральное значение. Второй вариант наступает тогда, когда количество данных четно, то есть вместо одного есть два центральных значения. Выход прост: берется средняя арифметическая из двух центральных значений:
В интервальных данных выбрать конкретное значение не представляется возможным. Медиану рассчитывают по определенному правилу.
Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов. Где накопленная доля впервые перевалила через 50% всех значений, там и медианный интервал.
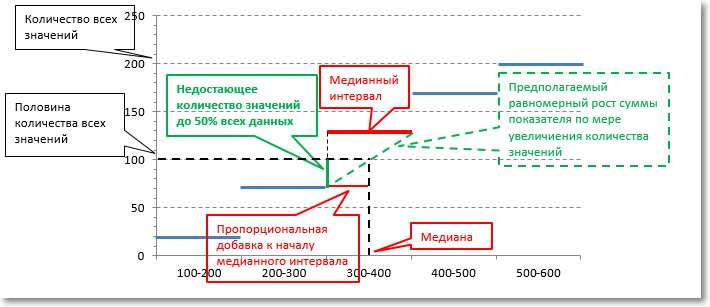
Не знаю, кто придумал формулу медианы, но исходили явно из того предположения, что распределение данных внутри медианного интервала равномерное (т.е. 30% ширины интервала – это 30% значений, 80% ширины – 80% значений и т.д.). Отсюда, зная количество значений от начала медианного интервала до 50% всех значений совокупности (разница между половиной количества всех значений и накопленной частотой предмедианного интервала), можно найти, какую долю они занимают во всем медианном интервале. Вот эта доля аккурат переносится на ширину медианного интервала, указывая на конкретное значение, именуемое впоследствии медианой.
Обратимся к наглядной схеме.
Немного громоздко получилось, но теперь, надеюсь, все наглядно и понятно. Чтобы при расчете каждый раз не рисовать такой график, можно воспользоваться готовой формулой. Формула медианы имеет следующий вид:
где xMe — нижняя граница медианного интервала;
iMe — ширина медианного интервала;
∑f/2 — количество всех значений, деленное на 2 (два);
S(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;
fMe — число наблюдений в медианном интервале.
Как нетрудно заметить, формула медианы состоит из двух слагаемых: 1 – значение начала медианного интервала и 2 – та самая часть, которая пропорциональна недостающей накопленной доли до 50%.
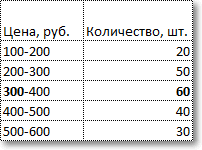
Для примера рассчитаем медиану по следующим данным.
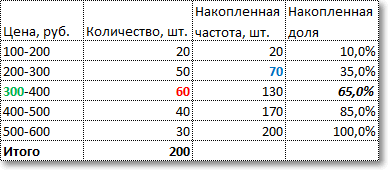
Требуется найти медианную цену, то есть ту цену, дешевле и дороже которой по половине количества товаров. Для начала произведем вспомогательные расчеты накопленной частоты, накопленной доли, общего количества товаров.
По последней колонке «Накопленная доля» определяем медианный интервал – 300-400 руб (накопленная доля впервые более 50%). Ширина интервала – 100 руб. Теперь остается подставить данные в приведенную выше формулу и рассчитать медиану.
То есть у одной половины товаров цена ниже, чем 350 руб., у другой половины – выше. Все просто. Средняя арифметическая, рассчитанная по этим же данным, равна 355 руб. Отличие не значительное, но оно есть.
Расчет медианы в Excel
Медиану для числовых данных легко найти, используя функцию Excel, которая так и называется — МЕДИАНА. Другое дело интервальные данные. Соответствующей функции в Excel нет. Поэтому нужно задействовать приведенную выше формулу. Что поделаешь? Но это не очень трагично, так как расчет медианы по интервальным данным – редкий случай. Можно и на калькуляторе разок посчитать.
Напоследок предлагаю задачку. Имеется набор данных. 15, 5, 20, 5, 10. Каково среднее значение? Четыре варианта:
а) 11;
б) 5;
в) 10;
г) 5, 10, 11.
Мода, медиана и среднее значение выборки – это разный способ определить центральную тенденцию в выборке.
Ниже видеоролик о том, как рассчитать медиану в Excel.
Поделиться в социальных сетях:
Мода
и медиана –
особого рода средние, которые используются
для изучения структуры вариационного
ряда. Их иногда называют структурными
средними, в отличие от рассмотренных
ранее степенных средних.
Мода
– это величина признака (варианта),
которая чаще всего встречается в данной
совокупности, т.е. имеет наибольшую
частоту.
Мода
имеет большое практическое применение
и в ряде случаев только мода может дать
характеристику общественных явлений.
Медиана
– это варианта, которая находится в
середине упорядоченного вариационного
ряда.
Медиана
показывает количественную границу
значения варьирующего признака, которой
достигла половина единиц совокупности.
Применение медианы наряду со средней
или вместо нее целесообразно при наличии
в вариационном ряду открытых интервалов,
т.к. для вычисления медианы не требуется
условное установление границ отрытых
интервалов, и поэтому отсутствие сведений
о них не влияет на точность вычисления
медианы.
Медиану
применяют также тогда, когда показатели,
которые нужно использовать в качестве
весов, неизвестны. Медиану применяют
вместо средней арифметической при
статистических методах контроля качества
продукции. Сумма абсолютных отклонений
варианты от медианы меньше, чем от любого
другого числа.
Рассмотрим
расчет моды и медианы в дискретном
вариационном ряду:
|
Стаж, |
Число |
Накопленные |
|
1 |
2 |
2 |
|
3 |
4 |
6 |
|
4 |
5 |
(11) |
|
8 |
4 |
15 |
|
10 |
1 |
16 |
|
ИТОГО: |
16 |
— |
Определить моду и медиану.
Мода
Мо =
4 года, так как этому значению соответствует
наибольшая частота f
= 5.
Т.е.
наибольшее число рабочих имеют стаж 4
года.
Для
того, чтобы вычислить медиану, найдем
предварительно половину суммы частот.
Если сумма частот является числом
нечетным, то мы сначала прибавляем к
этой сумме единицу, а затем делим пополам:
Ме=16/2=8
Медианой
будет восьмая по счету варианта.
Для
того, чтобы найти, какая варианта будет
восьмой по номеру, будем накапливать
частоты до тех пор, пока не получим сумму
частот, равную или превышающую половину
суммы всех частот. Соответствующая
варианта и будет медианой.
Ме
= 4 года.
Т.е.
половина рабочих имеет стаж меньше
четырех лет, половина больше.
Если
сумма накопленных частот против одной
варианты равна половине сумме частот,
то медиана определяется как средняя
арифметическая этой варианты и
последующей.
Вычисление
моды и медианы в интервальном вариационном
ряду
Мода
в интервальном вариационном ряду
вычисляется по формуле
где ХМ0
— начальная
граница модального интервала,
hм0
– величина модального интервала,
fм0,
fм0-1,
fм0+1
– частота
соответственно модального интервала,
предшествующего модальному и последующего.
Модальным
называется такой интервал, которому
соответствует наибольшая частота.
Пример
1
|
Группы |
Число |
Накопленные |
|
1 |
2 |
3 |
|
До |
4 |
4 |
|
2-4 |
23 |
27 |
|
4-6 |
20 |
47 |
|
6-8 |
35 |
82 |
|
8-10 |
11 |
93 |
|
свыше |
7 |
100 |
|
ИТОГО: |
100 |
— |
Определить
моду и медиану.
Решение.
Модальный
интервал [6-8], т.к. ему соответствует
наибольшая частота f
= 35. Тогда:
Хм0=6,
fм0=35
hм0=2,
fм0-1=20
fм0+1=11
Вывод:
Наибольшее число рабочих имеет стаж
примерно 6,7 лет.
Для
интервального ряда Ме вычисляется по
следующей формуле:
где Хме
–
нижняя граница медиального интервала,
hме
– величина медиального интервала,
–
половина суммы частот,
fме
– частота медианного интервала,
Sме-1
–сумма
накопленных частот интервала,
предшествующего медианному.
Медианный
интервал – такой интервал, которому
соответствует кумулятивная частота,
равная или превышающая половину суммы
частот.
Определим
медиану для нашего примера.
Найдем:
т.к
82>50, то медианный интервал [6-8].
Тогда:
Хме
=6, fме
=35,
hме
=2, Sме-1=47,
Вывод: Половина рабочих имеет стаж
меньше 6,16 лет, а половина имеет стаж
больше, чем 6,16 лет.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

В поисках средних значений: разбираемся со средним арифметическим, медианой и модой

Иногда при работе с данными нужно описать множество значений каким-то одним числом. Например, при исследовании эффективности сотрудников, уровня вовлеченности в аккаунте, KPI или времени ответа на сообщения клиентов. В таких случаях используют меры центральной тенденции. Их можно называть проще — средние значения.
Но в зависимости от вводных данных, находить среднее значение нужно по-разному. Основной набор задач закрывается с использованием среднего арифметического, медианы и моды. Но если выбрать неверный способ — выводы будут необъективны, а результаты исследования нельзя будет признать действительными. Чтобы не допустить ошибку, нужно понимать особенности разных способов нахождения средних значений.

Cтратег, аналитик и контент-продюсер. Работает с агентством «Палиндром».

Как считать среднее арифметическое
Использовать среднее арифметическое стоит тогда, когда множество значений распределяются нормально ― это значит, что значения расположены симметрично относительно центра. Как выглядит нормальное распределение на графике и в таблице, можно посмотреть на примере:


Если данные распределяются как в примерах — вам повезло. Можно без лишних заморочек считать среднее арифметическое и быть уверенным, что выводы будут объективны. Однако, нормальное распределение на практике встречается крайне редко, поэтому среднее арифметическое в большинстве случаев лучше не использовать.
Как рассчитать
Сумму значений нужно поделить на их количество. Например, вы хотите узнать средний ER за 4 дня при нормальном распределении значений и без аномальных выбросов. Для этого считаем среднее арифметическое: складываем ER всех дней и делим полученное число на количество дней.
Если хотите автоматизировать вычисления и узнать среднее арифметическое для большого числа показателей — используйте Google Таблицы:
- Заполните таблицу данными.
- Щелкните по пустой ячейке, в которую хотите записать среднее арифметическое.
- Введите «=AVERAGE(» и выделите ряд чисел, для которых нужно вычислить среднее арифметическое. Нажмите «Enter» после ввода формулы.
Когда можно не использовать
Если данные распределены ненормально, то наши расчеты не будут отражать реальную картину. На ненормальность распределения указывают:
- Отсутствие симметрии в расположении значений.
- Наличие ярко выраженных выбросов.
Как пример ненормального распределения (с выбросами) можно рассматривать среднее время ответа на комментарии по неделям:
Если посчитать среднее значение для такого набора данных с помощью среднего арифметического, то получится завышенное число. В итоге наши выводы будут более позитивными, чем реальное положение дел. Еще стоит учитывать, что выбросы могут не только завышать среднее значение, но и занижать его. В таком случае вы получите более скромный показатель, который не будет соответствовать реальности.
Например, в группе «Золотое Яблоко» во ВКонтакте иногда публикуют конкурсные посты. Они набирают более высокие показатели вовлеченности чем обычные публикации. Если посчитать средний ER с учетом конкурсов, мы получим 0,37%, а без учета конкурсов — только 0,29%. Аналогичная ситуация с числом комментариев. С конкурсами в среднем получаем 917 комментариев, а без конкурсов — всего лишь 503. Очевидно, что из-за розыгрышей средние показатели вовлеченности завышаются. В этом случае конкурсные посты следует исключить из анализа, чтобы объективно оценить эффективность контента в группе.
Еще часто бывает так, что данных очень много, заметны явные выбросы, но на их обработку и исключение аномальных значений не хватит ни времени, ни терпения. Тем более нет гарантий, что исключив выбросы, вы получите нормальное распределение. В таком случае лучше подсчитать средние значения, используя медиану.
Как найти медиану и когда ее применять
Если вы имеете дело с ненормальным распределением или замечаете значительные выбросы — используйте медиану. Так можно получить более адекватное среднее значение, чем при использовании среднего арифметического. Чтобы понять, как работать с медианой, рассмотрим аналогичный пример с ненормальным распределением времени ответов на комментарии.
Ниже в таблице уже введены данные из графика и рассчитано среднее время ответа с помощью среднего арифметического и медианы. Из расчетов видна наглядная разница между средним арифметическим и медианой ― она составляет 17 минут. Такое различие появляется из-за низкого темпа работы на выходных и в нестандартных ситуациях, когда к ответу на сообщения нужно относиться с особой ответственностью (события конца февраля). Подобные выбросы сильно завышают среднее арифметическое, а вот на медиану они практически не влияют. Поэтому если хотите посчитать среднее значение избегая влияния выбросов, — используйте медиану. Такие данные будут без искажений.
Как рассчитать
Разберем на примере. В аккаунте опубликовали семь постов и они набрали разное количество комментариев: 35, 105, 2, 15, 2, 31, 1. Чтобы вычислить медиану, нужно пройти два этапа:
- Расположите числа в порядке возрастания. Итоговый ряд будет выглядеть так: 1, 2, 2, 15, 31, 35, 105.
- Найдите середину сформированного ряда. В центре стоит число 15 — его и нужно считать медианой.
Немного сложнее найти медиану, если вы работаете с четным количеством чисел. Например, вы собрали количество лайков на последних шести постах: 32, 48, 36, 201, 52, 12. Чтобы найти медиану, выполните три действия:
- Расставьте числа по возрастанию: 12, 32, 36, 48, 52, 201.
- Возьмите два из них, наиболее близких к центру. В нашем случае — это 36 и 48.
- Сложите два этих числа и разделите на два: (36 + 48) / 2 = 42. Результат и есть медиана.
Чтобы вычислять медиану быстрее и обрабатывать большие объемы данных — используйте Google Таблицы:
- Внесите данные в таблицу.
- Щелкните по свободной ячейке, в которую хотите записать медиану.
- Введите формулу «=MEDIAN(» и выделите ряд чисел, для которых нужно рассчитать медиану. Нажмите «Enter», чтобы все посчиталось.
Когда можно не использовать
Если данные распределены нормально и вы не видите заметных выбросов — медиану можно не использовать. В этом случае значение среднего арифметического будет очень близким к медиане. Можете выбрать любой способ нахождения среднего, с которым вам работать проще. Результат от этого сильно не изменится.
Что такое мода и где ее использовать
Мода ― это самое популярное/часто встречающееся значение. Например, стоит задача узнать, сколько комментариев чаще всего набирают посты в аккаунте. В этом случае можно не высчитывать среднее арифметическое или медиану ― лучше и проще использовать моду.
Еще пример. Нужно узнать, в какое время аудитория чаще всего взаимодействует с публикациями. Для этого можно посчитать данные вручную или использовать готовую таблицу из LiveDune (вкладка «Вовлеченность» ― таблица «Лучшее время для поста»). По ее данным ― больше всего реакций пользователи оставляют в среду в 16 часов. Это время и есть мода. Таким образом, если вам нужно найти самое популярное значение, а не классическое среднее — проще использовать моду.
Как рассчитать
Чтобы найти наиболее часто встречающееся значение в наборе данных, нужно посмотреть, какое число встречается в ряду чаще всех. Например, для ряда 5, 4, 2, 4, 7 ― модой будет число 4.
Иногда в ряде значений встречается несколько мод. Например, ряду 7, 7, 21, 2, 5, 5 свойственны две моды — 7 и 5. В этом случае совокупность чисел называется мультимодальной. Также поиск моды можно упростить с помощью Google Таблиц:
- Внесите значения в таблицу.
- Щелкните по ячейке, в которую хотите записать моду.
- Введите формулу «=MODE(» и выделите ряд чисел, для которых нужно вычислить моду. Нажмите «Enter».
Однако важно иметь в виду, что табличная функция выдает только самую меньшую моду. Поэтому будьте внимательны — можно упустить из виду несколько мод.
Когда использовать не стоит
Моду нет смысла использовать, если вас не просят найти самое популярное значение. Там, где надо найти классическое среднее значение, про моду лучше забыть.
Памятка по использованию
Среднее арифметическое
Как находим: сумма чисел / количество чисел.
Используем: если данные распределены нормально и нет ярких выбросов.
Не используем: если видим явные выбросы или ненормальное распределение.
Медиана
Как находим: располагаем числа в порядке возрастания и находим середину сформированного ряда.
Используем: если работаем с ненормальным распределением или видим выбросы.
Не используем: если выбросов нет и распределение нормальное.
Мода
Как находим: определяем значение, которое чаще всего встречается в ряду чисел.
Используем: если нужно найти не среднее, а самое популярное значение.
Не используем: если нужно найти классическое среднее значение.
Только важные новости в ежемесячной рассылке
Нажимая на кнопку, вы даете согласие на обработку персональных данных.

Подписывайся сейчас и получи гайд аудита Instagram аккаунта
Маркетинговые продукты LiveDune — 7 дней бесплатно
Наши продукты помогают оптимизировать работу в соцсетях и улучшать аккаунты с помощью глубокой аналитики

Анализ своих и чужих аккаунтов по 50+ метрикам в 6 соцсетях.
Оптимизация обработки сообщений: операторы, статистика, теги и др.
Автоматические отчеты по 6 соцсетям. Выгрузка в PDF, Excel, Google Slides.
Контроль за прогрессом выполнения KPI для аккаунтов Инстаграм.
Аудит Инстаграм аккаунтов с понятными выводами и советами.
Поможем отобрать «чистых» блогеров для эффективного сотрудничества.