Задача.
Найдем медиану треугольника, проведенную к большей его стороне, если стороны треугольника равны 17 см, 23 см и 37 см.
Решение.
Дано: ABC,
BC=17 см, AC=23 см, AB=37 см,
BO — медиана.
Найти: BO.
Решение.
1) Отложим на луче BO отрезок OD, причем BO=OD.
2) Соединим точки А и D, C и D.
3) из полученного четырехугольника ABCD:
отрезки CO=AO (поскольку BO является медианой треугольника ABC согласно условию);
BO=DO (по результатам построения).
Получаем, что диагонали четырехугольника ABCD точкой пересечения делятся пополам, следовательно, данный четырехугольник ABCD является параллелограммом (согласно признаку).
4) Используем свойства диагоналей параллелограмма:
По построению :
Ответ. 26,4 см.
При решении этой задачи мы, по сути, вывели формулу для нахождения медианы треугольника по трем его сторонам. Поскольку медиану принято обозначать буквой m, а в индексе ставить обозначение стороны, к которой она проведена, то медиана, проведенная к стороне b, находится по формуле:
Аналогичным образом записываются формулы для нахождения остальных двух медиан.
Введение
Наверняка за то время, что вы изучаете геометрию, вы решили множество задач, в условии которых встречались медианы или биссектрисы. Обычно наличие таких слов предполагало лишь формальное использование определения медианы или биссектрисы, то есть то, что какая-то сторона либо какой-то угол разделены пополам.
Чуть реже мы использовали специфические свойства медиан и биссектрис. Но что делать, если нужно найти длину самой медианы или биссектрисы? Сейчас мы об этом и поговорим.
[00:0:54/Теорема о сторонах и диагоналях параллелограмма]
Докажем сначала полезную вспомогательную теорему о параллелограмме.
Теорема
В параллелограмме сумма квадратов диагоналей равна сумме квадратов сторон: .
Доказательство
Рассмотрим треугольники и
(Рис. 1).
Рис. 1. Иллюстрация к доказательству теоремы
По теореме косинусов для треугольника имеем
.
По теореме косинусов для треугольника имеем
.
Теперь заметим, что и
– секущая, то есть углы
и
– внутренние односторонние, а значит, их сумма равна
. Следовательно, их косинусы равны по модулю и противоположны по знаку:
. Учитывая это, сложим два равенства, получаем:
.
Теорема доказана.
Длина медианы
Эта теорема и сама по себе довольно полезна, потому что с ее помощью можно быстро найти недостающую сторону или диагональ параллелограмма. Но для нас сейчас особенно важно, что именно с помощью этой теоремы мы получим формулу для вычисления длины медианы треугольника. Для этого воспользуемся одним полезным стандартным приёмом при решении геометрических задач – удвоением медианы.
Теорема
Длину медианы треугольника можно вычислить по формуле: (Рис. 2).
Рис. 2. Иллюстрация к теореме о длине медианы треугольника
Доказательство
Продлим медиану на ее длину за точку
– получим точку
. Заметим, что
– параллелограмм по признаку: диагонали делятся точкой пересечения пополам (Рис. 3).
Рис. 3. Удвоение медианы
Значит, к нему можно применить доказанную нами теорему о сторонах и диагоналях параллелограмма:
Теорема доказана.
Итак, теперь мы умеем находить медиану треугольника, зная длины трёх его сторон. Воспользуемся этим для решения различных задач.
Примеры
Пример 1
Стороны треугольника равны и
. Найти медиану, проведенную к большей стороне.
Решение
Воспользуемся формулой для длины медианы: .
Подставляем в неё известные из условия длины сторон:
Ответ: .
Пример 2
В треугольнике :
,
, медиана
. Найти
.
Решение
Воспользуемся формулой для длины медианы и подставим в неё данные из условия:
Ответ: .
Формула длины медианы применяется и для доказательства теорем.
Доказательство теоремы
Теорема
Если в треугольнике две медианы равны, то он равнобедренный.
Доказательство
Пусть (Рис. 1).
Рис. 1. Иллюстрация к теореме
Выразим длины обеих медиан через длины сторон треугольника и приравняем полученные формулы:

Получаем, что треугольник равнобедренный. Что и требовалось доказать.
Длина биссектрисы
Длину биссектрисы ищут гораздо реже. Однако формула для вычисления её длины может быть полезна для решения некоторых задач.
Теорема
Длину биссектрисы треугольника можно вычислить по формуле: (Рис. 4).
Рис. 4. Иллюстрация к теореме
Доказательство
Воспользуемся методом площадей. Запишем формулы для вычисления площади некоторых треугольников:
С другой стороны, площадь треугольника равна сумме площадей двух непересекающихся треугольников, из которых он состоит: . Тогда
Теорема доказана.
Пример
Рассмотрим задачу, которую можно решить, используя полученную формулу.
Задача
Пусть в треугольнике ,
,
. Требуется найти биссектрису
(Рис. 5).
Рис. 5. Иллюстрация к задаче
Решение
Воспользуемся полученной формулой для длины биссектрисы:
Нахождение биссектрисы по трём сторонам
Можно ли найти длину биссектрисы, если известны только длины трёх сторон треугольника? Конечно, можно по теореме косинусов найти косинус соответствующего угла треугольника, а затем по формуле косинуса двойного угла найти косинус половины угла и применить доказанную нами формулу длины биссектрисы. Но есть и другой алгоритм.
Пример
Пусть в треугольнике :
и
. Найти биссектрису
(Рис. 1).
Рис. 1. Иллюстрация к условию задачи
Решение
1. Первым делом найдем . Заметим, что по свойству биссектрисы
, значит,
.
2. Далее по теореме косинусов для треугольника находим косинус угла
:
3. Теперь применим теорему косинусов к треугольнику :
Если этот метод вам понравился больше, то можно использовать для нахождения длины биссектрисы и его. Впрочем, в формулу подставлять гораздо проще.
Кстати, если даны три стороны, то есть еще одна формула, позволяющая найти длину биссектрисы: где
и
– отрезки, на которые сторона
делится биссектрисой (Рис. 6).
Рис. 6. Нахождение биссектрисы по трем сторонам
Доказательство
Пусть – точка пересечения продолжения биссектрисы
и окружности, описанной около
(Рис. 1).
Рис. 1. Иллюстрация к доказательству
Тогда треугольники и
подобны (одна пара углов равна по определению биссектрисы, а углы
и
– вписанные и опираются на одну дугу).
Значит, , то есть
.
Осталось заметить, что по теореме о пересекающихся хордах: , подставив это в полученное равенство, получим требуемое:
Заключение
На этом уроке мы познакомились с формулами для вычисления длины медианы и биссектрисы в треугольнике. Помимо этого, доказали важную теорему о сторонах и диагоналях параллелограмма и решили несколько задач на применение выведенных формул.
Список рекомендованной литературы
- Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009.
- Геометрия 11 класс, А.В. Погорелов. М.: Просвещение, 2002.
- Геометрия. 11 класс. Рабочая тетрадь. Бутузов В.Ф., Глазков Ю.А., Юдина И.И. 8-е изд. – М.: Просвещение, 2013.
Рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «syl.ru» (Источник)
- Интернет-портал «www-formula.ru» (Источник)
- Интернет-портал «zdesformula.ru» (Источник)
Домашнее задание
- Вычислите длину биссектрисы треугольника
, проведённую из вершины
, если
.
- Длины катетов прямоугольного треугольника равны
и
. Найдите длину биссектрисы прямого угла треугольника.
- В равнобедренном треугольнике длина боковой стороны равна
. Медиана, проведённая к боковой стороне, равна
. Найдите длину основания треугольника.
�������
������� ������������ ����� 11, 13 � 12. ������� �������,
�����ģ���� � ������� �������.
���������
�������������� �������� � ����� ��������� ����������
��������������� ��� �������� ��� ������� ������������.
�������
����� AM — ������� �������������� ������������ ABC, � �������
AB = 12, AC = 11, BC = 13. �� ����������� ������� AM �� ����� M
������� ������� MK, ������ AM. ����� ABKC — ��������������. ��
������� � ����� ��������� ���������� ���������������
AK2 + BC2 = 2AB2 + 2AC2,
������
AK2 = 2AB2 + 2AC2 — BC2 = 288 + 242 — 169 = 361 = 192.
�������������,
AM = AK =
.
�����
.
��������� � ���������� �������������
| web-���� | |
| �������� | ������� ����� �� ��������� �.�.������� |
| URL | http://zadachi.mccme.ru |
| ������ | |
| ����� | 2651 |
Определение и свойства медианы треугольника
В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.
Определение медианы треугольника
Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.
Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).
Свойства медианы
Свойство 1 (основное)
Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.
В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:
Свойство 2
Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.
Свойство 3
Три медианы делят треугольник на 6 равновеликих треугольников.
Свойство 4
Наименьшая медиана соответствует большей стороне треугольника, и наоборот.
- AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
- AB – самая короткая сторона, следовательно, медиана CD – самая длинная.
Свойство 5
Допустим, известны все стороны треугольника (примем их за a, b и c).
Длину медианы ma, проведенную к стороне a, можно найти по формуле:
Примеры задач
Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.
Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S△ = 5 см 2 ⋅ 6 = 30 см 2 .
Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.
Решение
Воспользуемся формулой, приведенной в свойстве 5:
Все формулы медианы треугольника
Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M — медиана, отрезок |AO|
c — сторона на которую ложится медиана
a, b — стороны треугольника
γ — угол CAB
Формула длины медианы через три стороны, ( M ):
Формула длины медианы через две стороны и угол между ними, ( M ):
По сторонам треугольника найти его медиану
Рассмотрим задачу, в которой требуется по сторонам треугольника найти его медиану.
Даны стороны треугольника. Найти длину медианы, проведенной к наибольшей стороне.
Дано: ∆ ABC,
сторона AC — наибольшая,
1) На луче BO отложим отрезок OD, OD=BO.
2) Проведем отрезки AD и CD.
3) Рассмотрим четырехугольник ABCD.
AO=CO (так как BO — медиана треугольника ABC по условию);
BO=DO (по построению).
Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).
так как BO=1/2 BD (по построению),
Если ввести обозначение
формула для нахождения медианы треугольника по его сторонам примет вид:
Запоминать эту формулу не обязательно. При решении конкретной задачи следует привести все рассуждения.
Если медиана проведена не к наибольшей, а к наименьшей либо средней по величине стороне, решение задачи аналогично.
Соответственно, формулы для нахождения длины медианы в этих случаях:
Приём, который применили для решения задачи — метод удвоения медианы.
http://www-formula.ru/mediantriangles
Ответ:
Mа = 2√3 см.
Объяснение:
По формуле медианы:
Ma = (1/2)·√(2b²+2c²-a²).
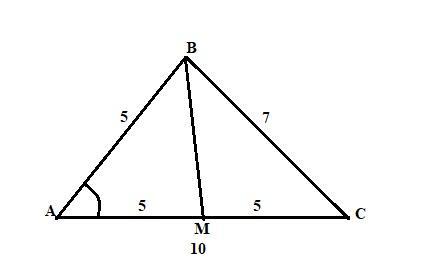
В нашем случае a = 10 см, b = 5 cм, с = 7 см.
Ma = (1/2)·√(50+98-100) = (√48)/2 = (2√12)/2 = √12 = 2√3 cм.
Или так:
Пусть дан треугольник АВС, в котором АВ = 5 см, ВС = 7 см и АС = 10 см.
Проведена медиана ВМ. АМ = МС = 5 см.
По теореме косинусов для угла А в треугольнике АВС имеем:
CosA = (AB²+BC²-AC²)/(2·AB·AC) = (100+25-49)/100 = 0,76.
По теореме косинусов для угла А в треугольнике АВМ имеем:
ВМ² = АВ²+АМ² — 2·АВ·АМ·СоsА = 25 + 25 — 2·5·5·0,76 = 12.
ВМ = √12 = 2√3 см.
Приложения: