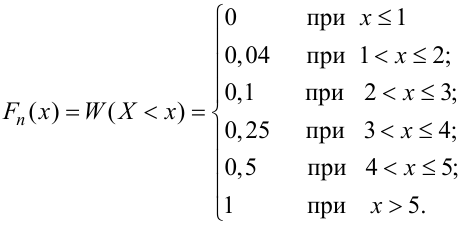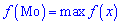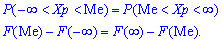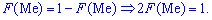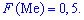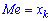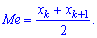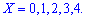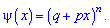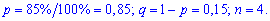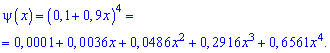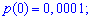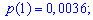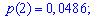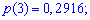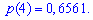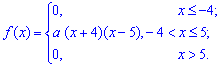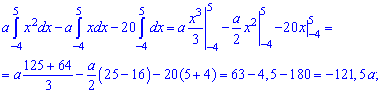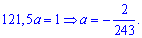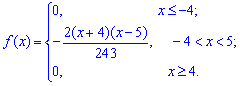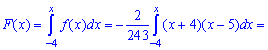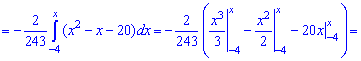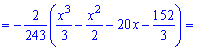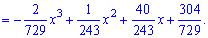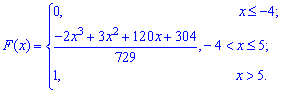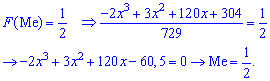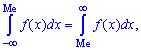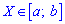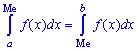Мода и медиана случайной величины.
Квантиль уровня случайной величины
- Краткая теория
- Примеры решения задач
Краткая теория
Кроме
математического ожидания и дисперсии, в теории вероятностей применяется еще ряд
числовых характеристик, отражающих те или иные особенности распределения.
Мода непрерывной и дискретной случайной величины
Модой
случайной величины называется ее наиболее вероятное значение, для которого
вероятность
или плотность вероятности
достигает максимума.
В
частности, наивероятнейшее значение числа успехов в схеме Бернулли – это мода
биномиального распределения.
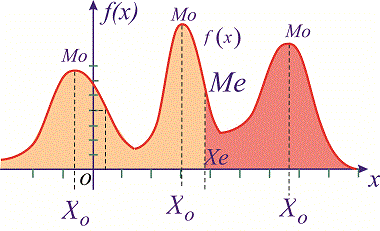
Если
вероятность или плотность вероятности достигает максимума не в одной, а в
нескольких точках, распределение называется полимодальным.
Полимодальное распределение
Медиана непрерывной и дискретной случайной величины
Медианой случайной величины
называют число
, такое, что
.
То есть вероятность того, что
случайная величина
примет
значение, меньшее медианы
или больше ее,
одна и та же и равна
.
Для дискретной случайной величины
это число может
не совпадать ни с одним из значений
. Поэтому медиану дискретной случайной величины
определяют как любое число
, лежащее между двумя соседними возможными значениями
и
такими, что
.
Для непрерывной случайной величины,
геометрически, вертикальная прямая
, проходящая через точку с абсциссой, равной
, делит площадь фигуры под кривой распределения на две
равные части.
Медиана на графике плотности вероятности непрерывной
случайной величины
Очевидно, что в точке
функция распределения непрерывной случайной
величины равна
, то есть
.
Медиана на графике функции распределения непрерывной
случайной величины
Квантили и процентные точки случайной величины
Наряду с отмеченными выше числовыми
характеристиками для описания случайной величины используется понятие квантилей
и процентных точек.
Квантилем уровня
(или
– квантилем)
называется такое значение
случайной
величины, при котором функция ее распределения принимает значение, равное
, то есть:
Некоторые квантили получили особое
называние. Очевидно, что введенная выше медиана случайной величины есть
квантиль уровня 0,5, то есть
. Квантили
и
получили
название соответственно верхнего и нижнего квантилей. Также в литературе
встречаются термины: децили (под которыми понимают квантили
) и процентили (квантили
).
С понятием квантиля тесно связано
понятие процентной точки. Под
точкой
подразумевается квантиль
, то есть такое значение случайной величины
, при котором
.
Смежные темы решебника:
- Структурные средние в статистике — мода, медиана, квантиль, дециль
- Дискретная случайная величина
- Непрерывная случайная величина
Примеры решения задач
Пример 1
Найти
моду, медиану, квантиль
и 40%-ну точку случайной величины
c плотностью распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Производная
не обращается в нуль.
Значения
на концах отрезка:
Следовательно,
мода:
Медиану
найдем из условия:
В нашем
случае получаем:
Значение
принадлежит отрезку
,
следовательно, искомая медиана:
Квантиль
найдем из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомый квантиль:
Найдем
40%-ную точку случайной величины
, или квантиль
из уравнения:
Значение
принадлежит отрезку
,
следовательно, искомая точка:
Ответ:
.
Пример 2
Найти
моду, медиану, квантиль
случайной величины
, заданной функцией
распределения:
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Найдем
плотность распределения:
Исследуем
функцию на наибольшее и наименьшее значение на отрезке
Производная:
Значения
функции
в стационарных точках и на концах отрезка:
Распределение
полимодальное:
Медиану
найдем из уравнения:
Итак,
медиана:
Квантиль
найдем из уравнения:
Итак:
Ответ:
.
- Краткая теория
- Примеры решения задач
Вводится лишь для НСВ, хотя
формально ее можно определить и для
ДСВ.
Определение 42. Медианой непрерывной
случайной величины называется такое
ее значение х = Ме, относительно
которого равновероятно получение
большего или меньшего значения случайной
величины, т. е. для которого справедливо
равенство:
,
( для НСВ безразлично
или
)
(по определению функции распределения).
Таким образом, медиана – это корень
уравнения
:
.
(3)
Геометрически: медиана – это
абсцисса точки, в которой площадь,
ограниченная кривой распределения,
делится пополам.
Замечание. В случае симметричного
модального распределения медиана
совпадает с мат. ожиданием и модой.
Когда медиана входит в формулы как
определенное число, то ее обозначают
hX.
Пп 2. Моменты
Данные характеристики описывают
некоторые свойства распределения
СВ. В механике, например, для описания
распределения масс существуют статические
моменты, моменты инерции…
Определение 43. Начальным моментом
s – того порядка для
ДСВ и НСВ называется математическое
ожидание s – той
степени этой случайной величины:
.
Замечание. При s
= 1
,
т. е. математическое ожидание – это
первый начальный момент.
а) Для дискретных случайных
величин:
.
(4)
Замечание. Определение совпадает
с определением начального момента
порядка s в механике,
если на оси (Ох) в точках х1 ,
х2, …,хn
сосредоточены соответственно
массы р1, р2 , …, рn.
b) Для
непрерывных случайных величин:
.
(5)
Определение 44. Центрированной
случайной величиной, соответствующей
величине Х, называется отклонение
случайной величины Х от ее
математического ожидания:
.
Рассмотрим математическое ожидание
центрированной ДСВ:
.
Аналогично, для НСВ
.
Центрирование СВ равносильно переносу
начала координат в среднюю, центральную
точку, абсцисса которой равна
математическому ожиданию.
Определение 45. Моменты центрированной
случайной величины называются центральными
моментами.
Определение 46. Центральным моментом
s – того порядка для
ДСВ и НСВ называется математическое
ожидание s – той
степени соответствующей центрированной
случайной величины:
.
а) Для дискретных случайных
величин:
. (6)
b) Для
непрерывных случайных величин:
.
(7)
Замечание. Для любой СВ центральный
момент 1-го порядка
равен
0:
,
так как мат. ожидание центрированной
СВ равно 0.
Рассмотрим подробнее центральные
моменты 2, 3, 4 порядков и выведем
соотношения, связывающие начальные и
центральные моменты.
– дисперсия
Определение 47. Дисперсией случайной
величины Х D[X]
называется мат ожидание квадрата
соответствующей центрированной случайной
величины:
а) Для дискретных случайных
величин: D[X]
=
.
(8)
b) Для
непрерывных случайных величин:
D[X]
=
.
(9)
Дисперсия случайной величины –
характеристика рассеивания,
разбросанности значений случайной
величины около ее мат. ожидания.
Когда дисперсия входит в формулы как
определенное число, то ее обозначают
DX.
Механическая интерпретация
D[X]:
Дисперсия – момент инерции заданного
распределения масс относительно центра
тяжести (мат. ожидания).
Рассмотрим ДСВ. (Для НСВ получаем
аналогично)
.
– связь между начальным и центральным
моментом 2-го порядка. (10)
Свойства
.
1.
,
где С – постоянная.
2.
.
3.
.
4.
для независимых СВ.
5.
,
a, b
– постоянные.
Замечание. D[X]
имеет размерность квадрата случайной
величины. Для более наглядной характеристики
рассеивания удобнее пользоваться
величиной, размерность которой совпадает
с размерностью случайной величины. Для
этого из D[X]
извлекают корень:
,
(11)
где
– среднее квадратическое отклонение
или стандарт случайной величины
Х.
Когда среднее квадратическое входит
в формулы как определенное число, то
его обозначают
.
Замечание. Математическое ожидание
и дисперсия характеризуют наиболее
важные черты распределения: его положение
и степень разбросанности. Для более
подробного описания применяются моменты
высших порядков.
– асимметрия
Асимметрия случайной величины –
характеристика асимметрии или
скошенности распределения значений
случайной величины.
Теорема. Если распределение
симметрично относительно мат. ожидания
(т. е. масса распределена симметрично
относительно центра тяжести), то все
моменты нечетного порядка (если они
существуют) равны нулю.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Числовые характеристики случайных величин:
Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.
Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.
Математическое ожидание случайной величины
Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся
Рассмотрим свойства математического ожидания.
- Математическое ожидание постоянной величины равно самой постоянной: М(С) = С. (5.3)
- Постоянный множитель можно выносить за знак математического ожидания, т.е. M(СX) = С·M(X). (5.4)
- Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е
- Математическое ожидание произведений конечного числа случайных величин равно произведению их математических ожиданий, т.е. M(XY) = M(X)·M(Y). (5.6)
- Если все значения случайной величины увеличить (или уменьшить) на постоянную С, то на эту же постоянную С увеличится (или уменьшится) математическое ожидание этой случайной величины:
- Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
Пример:
Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение:
Используя свойства 1, 2, 3 математического ожидания, находим
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дисперсия случайной величины
Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
Для дискретной случайной величины X эта формула принимает вид:
Для непрерывной случайной величины: 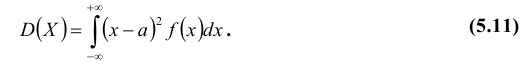
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: 

Рассмотрим свойства дисперсии.
- Дисперсия постоянной величины равна нулю:
- Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат, т.е.
- Дисперсия алгебраической суммы конечного числа случайных величин равна сумме их дисперсий, т.е.
- Дисперсия разности двух независимых случайных величин равна сумме их дисперсий, т.е.
Пример №1
Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.
Решение:
Используя свойства дисперсии, находим
Среднее квадратическое отклонение случайной величины
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии:
Свойства среднего квадратического отклонения вытекают из свойств дисперсии.
Мода и медиана. Квантили
Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.
Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.
Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого 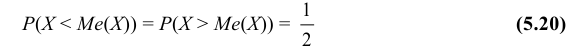
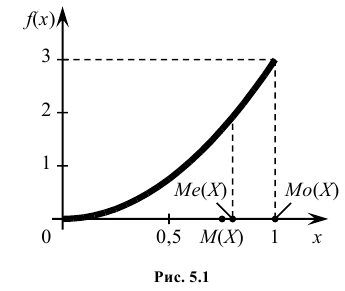
Пример №2
Найти моду, медиану случайной величины Х с плотностью вероятности
Решение:
Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия 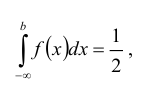
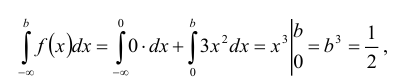
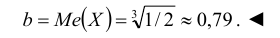
Наряду с модой и медианой для описания случайной величины используется понятие квантиля.
Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.
Пример №3
По данным примера 5.3 найти квантиль
Решение:
Находим функцию распределения 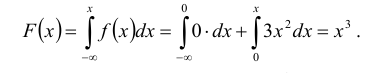
Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.
Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины: 

Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания:
Для дискретной случайной величины формула центрального момента имеет вид:
Для непрерывной случайной величины: 
Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.
Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на 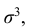
Полученная величина А называется коэффициентом асимметрии случайной величины: 
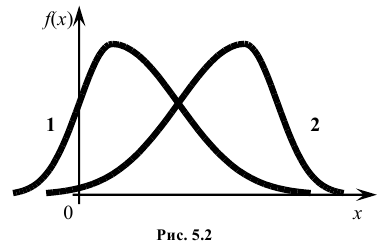
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А < 0).
Четвертый центральный момент μ4 служит для характеристики крутости (островершинности или плосковершинности) распределения.
Эксцессом случайной величины называется число 
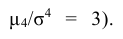
Числовые характеристики независимых испытаний
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (т.е. повторные независимые испытания). В этом случае математическое ожидание числа появлений события А в n испытаниях находится по формуле M(X) = np, (5.30) а дисперсия по формуле D(X) = npq. (5.31)
Одинаково распределенные взаимно независимые случайные величины
Рассмотрим n взаимно независимых случайных величин 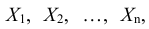
Обозначим среднее арифметическое n взаимно независимых случайных величин через
Сформулируем положения, устанавливающие связь между числовыми характеристиками среднего арифметического 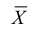
- Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию а каждой из величин:
- Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в
раз меньше дисперсии D каждой из величин:
- Среднее квадратическое отклонение n одинаково распределенных взаимно независимых случайных величин в n раз меньше среднего квадратического отклонения σ каждой из величин:
Пример:
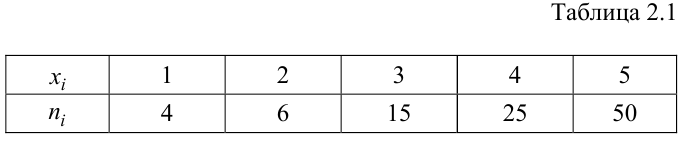
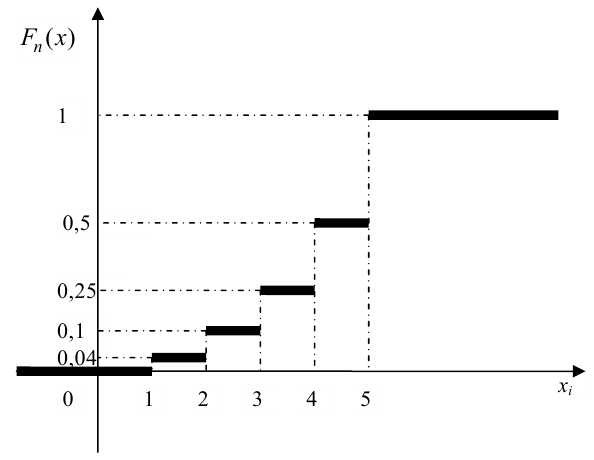
По данному распределению выборки (табл. 2.1) найти эмпирическую функцию распределения.
Решение. Определяем объем выборки:
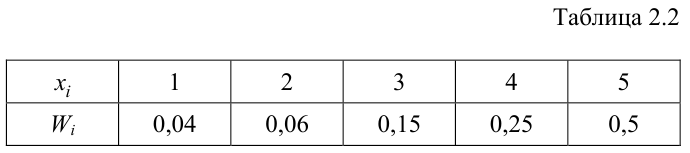
Определяем относительные частоты вариант (табл. 2.2):
Так как значение 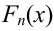
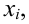
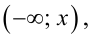
График примет вид:
- Нормальный закон распределения
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
Мода и медиана функции плотности распределения f(x)
Задача 5. Плотность распределения вероятностей случайной величины Х имеет вид
1. Найти:
а) параметр распределения С (в виде дроби);
а) математическое ожидание M(X);
б) дисперсию D(X) и среднее квадратическое отклонение σ(Х);
в) функцию распределения F(x) случайной величины X;
г) моду M0;
д) медиану Me;
е) вероятность осуществления неравенств и
.
2. Построить графики функций f(x) и F(x). Изобразить на графике функции f(x) найденные характеристики и вероятности.
Решение находим с помощью калькулятора.
Случайная величина Х задана плотностью распределения f(x):
0, x ≤ 0
2•A(8/5-x), 0 < x < 8/5
0, x ≥ 8/5
Найдем параметр A из условия:

или
64/25*A-1 = 0
Откуда,
A = 25/64
Поскольку находили квадрат A, то
а) Математическое ожидание.

б) Дисперсия.
= -25/128•(8/5)4+5/12•(8/5)3 — (-25/128•04+5/12•03) — (8/15)2 = 32/225
Среднеквадратическое отклонение.
в) Функция распределения F(x) случайной величины X.

г) Мода M0.
Модой M0(X) называют то возможное значение X, при котором плотность распределения имеет максимум.
Построим график функции плотности распределения.
Как видим, максимум функции соответствует x = 0.
Mo( 0) = 2•25/64(8/5-0) = 5/4
д) Медиана Me.
Медианой Me(X) называют то возможное значение X, при котором ордината f(x) делит пополам площадь, ограниченную кривой распределения.
Необходимо найти такое x, при котором функция распределения равна ½.
Решая уравнение:
получаем:
Поскольку функция ограничена на интервале (0; 1,6), то искомое значение x = 0,46.
Построим график функции распределения.
е) Вероятность осуществления неравенств и
.
Перейти к онлайн решению своей задачи
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Для нахождения моды и медианы случайной величины необходимы хорошие умения интегрировать и знания следующего теоретического материала. Модой 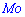
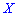
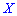
В зависимости от вида функции 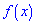
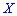
Существуют и такие распределения, которые не имеют моды, их называют антимодальными. Медианой 
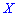
Графически мода и медиана изображенные на рисунке
При таком значению случайной величины график функции распределения делится на части с одинаковой площадью. Непрерывная случайная величина имеет только одно значение медианы. Для дискретной случайной величины медиану обычно не определяют, однако в некоторой литературе приводятся правила, согласно которым, для ряда случайных величин размещенных в порядке возрастания (вариационного ряда) моду определяют распределения: если есть нечетное количество случайных величин 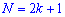
в случае четного количества 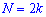
Рассмотрим примеры определения моды и медианы.
Пример 1. В развлекательном центре работник обслуживает четыре дорожки для боулинга. Вероятность того, что какая-то дорожка нуждается в уборке в течение смены является постоянной величиной с вероятностью 85%.
Построить закон распределения вероятностей дискретной случайной величины 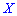
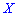
Решение. Случайной величина может принимать значения
Вероятности появления значений определяем по образующей функцией
Для заданной задачи входные величины принимают значения
Искомые вероятности входят множителями при степенях аргумента
Закон распределения вероятностей запишем в виде таблицы
С таблице определяем моду 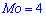
Пример 2. По заданной плотностью вероятностей
найти параметр 
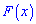
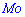
Решение. Применяя условие нормирования выполняем интегрирование
после того определяем параметр
Плотность вероятностей, учитывая найденное значение будет иметь вид
а ее график изображен на рисунке ниже
Из графика плотности вероятностей видим, что мода принимает значение 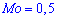

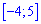
Функция распределения иметь следующий вид
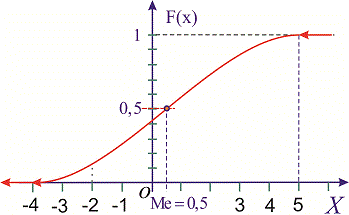
а ее график будет иметь вид
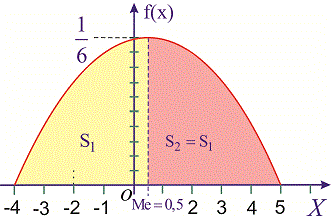
Для определения медианы случайной величины 
Медиану 
для дискретной случайной величины из промежутка
Таким образом медиану 
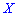
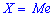
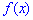
——————————-
Задача на определение моды и медианы случайной величины встречаются на практике не так часто, как плотности распределения вероятностей, однако вышеприведенный теоретический материал и решения распространенных примеров помогут Вам находить эти величины без больших затрат времени. При необходимости Вы всегда можете заказать решение задач по теории вероятностей в нас.


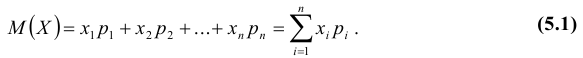
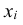
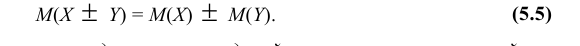


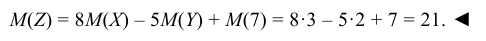







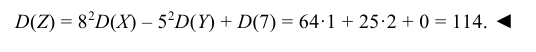
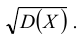

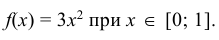

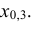



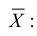
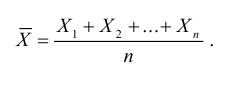

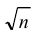 раз меньше дисперсии D каждой из величин:
раз меньше дисперсии D каждой из величин: