Как найти медиану проведенную к катету - Исправление недочетов и поиск решений вместе с Examum.ru

Что можно сказать о прямоугольном треугольнике, в котором известны медианы, проведенные к катетам?

Медиана, проведённая к катету, разбивает исходный треугольник на два треугольника, один из которых также прямоугольный. Эти треугольники имеют равные площади.

В точке пересечения медианы делятся в отношении 2:1, считая от вершины. Если провести третью медиану, исходный треугольник разбивается на 6 равновеликих треугольников.

Из двух медиан больше та, которая проведена к наименьшей стороне. Таким образом, медиана, проведённая к гипотенузе — наименьшая.

По известным длинам проведённых к катетам медиан можно найти остальные стороны прямоугольного треугольника.

Задача.

В прямоугольном треугольнике медианы, проведенные к катетам, равны m1 и m2. Найти катеты, периметр и площадь этого треугольника.

Дано:∆ABC, ∠C=90º,

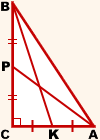
AP, CF — медианы, AP=m1, BK=m2

Найти:

$[AC,BC,{P_{Delta ABC}},{S_{Delta ABC}}.]$

Решение:

Для определенности, возьмём BC>AC, следовательно, m1<m2.

Пусть CP=x, CK=y. Так как AP BK — ABC, AC=2x, BC=2y.

Из прямоугольного треугольника ACP по теореме Пифагора

$[A{C^2} + C{P^2} = A{P^2},]$

$[4{x^2} + {y^2} = m_1^2.]$

Аналогично, из треугольника BCK

$[B{C^2} + C{K^2} = B{K^2},]$

$[4{y^2} + {x^2} = m_2^2.]$

$[left{ begin{array}{l} 4{x^2} + {y^2} = m_1^2\ {x^2} + 4{y^2} = m_2^2 Получили систему уравнений end{array} right.]$

Умножим второе уравнение системы на -4 и сложим с первым:

$[ - 15{y^2} = m_1^2 - 4m_2^2]$

$[{y^2} = frac{{m_1^2 - 4m_2^2}}{{ - 15}} = frac{{4m_2^2 - m_1^2}}{{15}},]$

$[y = sqrt {frac{{4m_2^2 - m_1^2}}{{15}}} .]$

Аналогично, умножив первое уравнение на -4 и сложив со вторым, получаем

$[ - 15{x^2} = - 4m_1^2 + m_2^2,]$

$[{x^2} = frac{{4m_1^2 - m_2^2}}{{15}},]$

$[x = sqrt {frac{{4m_1^2 - m_2^2}}{{15}}} .]$

$[AC = 2sqrt {frac{{4m_1^2 - m_2^2}}{{15}}} ,BC = 2sqrt {frac{{4m_2^2 - m_1^2}}{{15}}} .]$

Из треугольника ABC по теореме Пифагора

$[A{B^2} = A{C^2} + B{C^2},]$

$[A{B^2} = 4cdotfrac{{4m_1^2 - m_2^2}}{{15}} + 4cdotfrac{{4m_2^2 - m_1^2}}{{15}} = frac{{12(m_1^2 + m_2^2)}}{{15}} = ]$

$[ = frac{4}{5}(m_1^2 + m_2^2),]$

$[AB = 2sqrt {frac{{m_1^2 + m_2^2}}{5}} .]$

Периметр треугольника ABC равен

$[{P_{Delta ABC}} = AB + BC + AC,]$

$[{P_{Delta ABC}} = 2(sqrt {frac{{m_1^2 + m_2^2}}{5}} + sqrt {frac{{4m_2^2 - m_1^2}}{{15}}} + sqrt {frac{{4m_1^2 - m_2^2}}{{15}}} ),]$

площадь —

$[{S_{Delta ABC}} = frac{1}{2} cdot AC cdot BC,]$

$[{S_{Delta ABC}} = frac{1}{2} cdot 2sqrt {frac{{4m_1^2 - m_2^2}}{{15}}} cdot 2sqrt {frac{{4m_2^2 - m_1^2}}{{15}}} = ]$

$[ = frac{2}{{15}}sqrt {(4m_1^2 - m_2^2)(4m_2^2 - m_1^2)} .]$

Поскольку медиана, проведённая к гипотенузе, равна её половине, можно найти третью медиану как

$[{m_3} = frac{1}{2}AB = sqrt {frac{{m_1^2 + m_2^2}}{5}} .]$

Запоминать эти формулы не нужно, при решении конкретной задачи достаточно повторить эти рассуждения.

Источник

Медиана прямоугольного треугольника, делящая гипотенузу пополам, равна получившимся половинам гипотенузы. Таким образом, медиана делит прямоугольный треугольник на два равнобедренных треугольника с катетами в виде оснований. Для того чтобы вычислить медиану прямоугольного треугольника, достаточно знать гипотенузу, два катета, или один катет и угол в треугольнике.
Найти медиану через гипотенузу:
Найти медиану через катеты:
Найти медиану через катет и угол:

Источник

Определение и свойства медианы прямоугольного треугольника

В данной статье мы рассмотрим определение и свойства медианы прямоугольного треугольника, проведенной к гипотенузе. Также разберем пример решения задачи для закрепления теоретического материала.

Определение медианы прямоугольного треугольника

Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Прямоугольный треугольник – это треугольник, в котором один из углов является прямым (90°), а два остальных – острыми ( Свойства медианы прямоугольного треугольника

Свойство 1

Медиана (AD) в прямоугольном треугольнике, проведенная из вершины прямого угла (∠BAC) к гипотенузе (BC), равна половине гипотенузы.

BC = 2AD
AD = BD = DC

Следствие: Если медиана равняется половине стороны, к которой она проведена, то данная сторона является гипотенузой, а треугольник – прямоугольным.

Свойство 2

Медиана, проведенная к гипотенузе прямоугольного треугольника, равняется половине квадратного корня из суммы квадратов катетов.

Для нашего треугольника (см. рисунок выше):

Это следует из теоремы Пифагора и Свойства 1.

Свойство 3

Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу описанной вокруг треугольника окружности.

Т.е. BO – это одновременно и медиана, и радиус.

Примечание: К прямоугольному треугольнику также применимы общие свойства медианы, независимо от вида треугольника.

Пример задачи

Длина медианы, проведенной в гипотенузе прямоугольного треугольника, составляет 10 см. А один из катетов равен 12 см. Найдите периметр треугольника.

Решение
Гипотенуза треугольника, как следует из Свойства 1, в два раза больше медианы. Т.е. она равняется: 10 см ⋅ 2 = 20 см.

Воспользовавшись теоремой Пифагора находим длину второго катета (примем его за “b”, известный катет – за “a”, гипотенузу – за “с”):
b 2 = с 2 – a 2 = 20 2 – 12 2 = 256.
Следовательно, b = 16 см.

Теперь мы знаем длины всех сторон и можем посчитать периметр фигуры:
P_△ = 12 см + 16 см + 20 см = 48 см.

Все формулы медианы прямоугольного треугольника

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c , пополам.

Медиана в прямоугольном треугольнике ( M ), равна, радиусу описанной окружности ( R ).

M — медиана

R — радиус описанной окружности

O — центр описанной окружности

с — гипотенуза

a, b — катеты

α — острый угол CAB

Медиана равна радиусу и половине гипотенузы, ( M ):

Формула длины через катеты, ( M ):

Формула длины через катет и острый угол, ( M ):

Медиана в прямоугольном треугольнике

Медиана в прямоугольном треугольнике — это отрезок, который соединяет вершину треугольника и середину противоположной стороны, то есть вершину острого угла с серединой противолежащего катета или вершину прямого угла с серединой гипотенузы.

Все медианы прямоугольного треугольника пересекаются в одной точке и делятся этой точкой в отношении два к одному, считая от вершины:

Из всех медиан прямоугольного треугольника в задачах чаще всего речь идет о медиане, проведенной к гипотенузе. Это связано с ее свойствами.

Свойства медианы, проведенной к гипотенузе:

1) Медиана, проведенная к гипотенузе, равна половине гипотенузы.

(в следующий раз рассмотрим доказательство этого свойства)

2) Медиана, проведенная к гипотенузе, равна радиусу описанной около прямоугольного треугольника окружности.

Пользуясь свойствами прямоугольного треугольника, длины медиан прямоугольного треугольника можно выразить через катеты и острые углы.

Например:

12 Comments

Информация очень хорошая. Правда не помогла мне решить задачу, которую мой сын не решил на контрольной. приведу условие:
Из прямого угла треугольника проведена медиана на гипотенузу. Длина медианы 6см. Определить катеты.

Петр, данных для определения катетов недостаточно. Длина гипотенузы в 2 раза больше длины медианы — 12 см. Это всё, что можно сказать по данным условия.

не правда надо провести высоту из прямого угла дальше все получится. один катет равен 6 а второй 2 корня из 22

Сумма квадратов катетов равна квадрату гипотенузы. Проверим 6^2+(2*корень из 22)^2
=36+4*22=36+88=124. Квадрат гипотенузы 12^2=144

попробуйте составить уравнение,обозначив 1 из катетов через х а 2-ой катет обозначьте буквами…x^2+BC^2=12^2…да числа не очень,но это 1 способ..решаю дальше:BC^2=12^2-x^2
BC^2=11x
X^2+11X=144
X^2=12
x(1 катет)=корню из 12,а «-ой катет=11 корней из 12….решал на основе теоремы пифагора

задача имеет бесконечное кол-во решений. решение возможно только в виде формулы или графика, где описана зависимость между катетами и гипотенузой

Да просто треугольник медианой делится на два треугольника с одинаковыми катетами, а дальше как уже предлагалось выше Пифагор во спасение))

А кто вам сказал, что медиана в прямоугольном треугольнике является еще и высотой? Откуда у вас два треугольника с одинаковыми катетами?

Спасибо за понятное объяснение, но у нас задача немного другая.
В прямоугольном треугольнике АВС угол С= 90 градусов,медиана ВВ1 равна 10 см.Найдите медианы АА1 СС1, если известно, что АС=12 см.( используя т.Пифагора.

1) Рассмотрим треугольник BB1C. В нём угол С равен 90 градусов, BB1=10 см, B1C=6 см (так как BB1 — медиана). По теореме Пифагора находим BC: BC=8 см. 2) Рассмотрим треугольник AA1C. В нём угол С равен 90 градусов, AC=12 см, AA1=4 см (так как BB1 — медиана). По теореме Пифагора находим AA1: AA1=4√10 см.3) Из треугольника ABC по теореме Пифагора найдём AB: AB=4√13 см. 4) CC1=1/2 AB (как медиана, проведённая к гипотенузе), CC1=2√13 см.
Где-то так.

источники:

http://www-formula.ru/medianrectangulartriangle

Медиана в прямоугольном треугольнике

Источник

Все формулы медианы прямоугольного треугольника

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.

Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M — медиана

R — радиус описанной окружности

O — центр описанной окружности

с — гипотенуза

a, b — катеты

α — острый угол CAB

Медиана равна радиусу и половине гипотенузы, (M):

Формула длины через катеты, (M):

Формула длины через катет и острый угол, (M):

Подробности

Автор: Administrator

Опубликовано: 08 октября 2011

Обновлено: 13 августа 2021

Источник

Определение медианы прямоугольного треугольника
Свойства медианы прямоугольного треугольника
- Свойство 1
- Свойство 2
- Свойство 3
Пример задачи

Определение медианы прямоугольного треугольника

Медиана – это отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Прямоугольный треугольник – это треугольник, в котором один из углов является прямым (90°), а два остальных – острыми (<90°).

Свойства медианы прямоугольного треугольника

Свойство 1

BC = 2AD
AD = BD = DC

Свойство 2

Для нашего треугольника (см. рисунок выше):

Это следует из теоремы Пифагора и Свойства 1.

Свойство 3

Т.е. BO – это одновременно и медиана, и радиус.

Пример задачи

Воспользовавшись теоремой Пифагора находим длину второго катета (примем его за “b”, известный катет – за “a”, гипотенузу – за “с”):
b² = с² – a² = 20² – 12² = 256.
Следовательно, b = 16 см.

Теперь мы знаем длины всех сторон и можем посчитать периметр фигуры:
P_△ = 12 см + 16 см + 20 см = 48 см.

Источник