Рассмотрим задачи, в которых требуется по рисунку на клетчатой бумаге найти длину медианы треугольника.
Задачи.
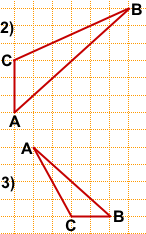
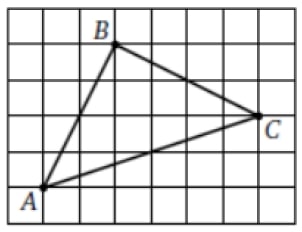
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его медианы, проведённой из вершины C.
Решение:
Медиана, проведённая из вершины C, соединяет точку C с серединой противолежащей стороны AB.
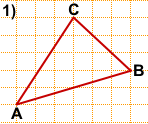
Следовательно, задачу начинаем с нахождения середины AB.
Как правило, сторона AB в таких задачах изображается не горизонтальным или вертикальным отрезком.
Чтобы найти середину AB, можно построить по клеточкам прямоугольник с диагональю AB и провести его вторую диагональ. По свойству прямоугольника, точка H пересечения диагоналей — середина AB.
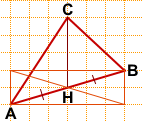
Длину медианы CH считаем по клеточкам — CH=4.
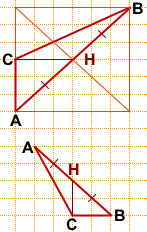
2) Аналогично предыдущей задаче, сначала найдём середину отрезка AB.
Можно достроить прямоугольник с диагональю AB, провести вторую диагональ и отметить точку H пересечения диагоналей.
Длину медианы CH находим по клеточкам:
CH=3.
3) Можно найти середину отрезка AB и без дополнительных построений.
Например, можно рассуждать так:
AH=BH как диагонали равных квадратов (со стороной 2 клетки), следовательно, точка H — середина AB, CH — медиана треугольника ABC.
CH=2.
Если медиана треугольника расположена не горизонтально либо вертикально, посчитать её длину по клеточкам не удастся.
4) В прямоугольном треугольнике длину медианы, проведённой к гипотенузе, можно найти, опираясь на соответствующее свойство.
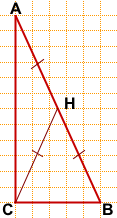
То есть для нахождения длины медианы нужно знать гипотенузу.
Длины катетов определяем по клеточкам: AC=12, BC=5.
По теореме Пифагора: AB²=AC²+BC²,
AB²=12²+5²=169, AB=13,
CH= 1/2 AB=6,5.
5) 
Середину отрезка AB — точку H — найдём как точку пересечения диагоналей прямоугольника с диагональю AB
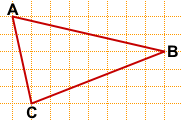
(достаточно провести вторую диагональ, прямоугольник можно не строить).
Длину диагонали по клеточкам определить не получится.
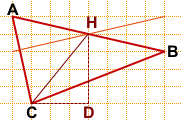
Достроим прямоугольный треугольник CHD с гипотенузой CH.
CD=3, HD=4.
CH находим по теореме Пифагора (можно также заметить, что CHD — египетский треугольник): CH=5.
Задания
Версия для печати и копирования в MS Word
Тип 18 № 311958 
i
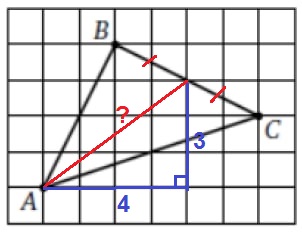
На рисунке изображён прямоугольный треугольник. Найдите длину медианы треугольника, проведённой из вершины прямого угла.
Спрятать решение
Решение.
Введем обозначения, как показано на рисунке и проведём медиану треугольника AH. В прямоугольном треугольнике ABC длины катетов равны 3 и 4, поэтому гипотенуза равна 
В прямоугольном треугольнике медиана, проведённая из прямого угла, равна половине гипотенузы, т. е. 5 : 2 = 2,5.
Ответ: 2,5.
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Спрятать решение
·
Помощь
Привет! Цель нашего проекта помочь тебе подготовиться к ЕГЭ (или ОГЭ).
У нас более 1000 заданий с подробным решением, сервис, запоминающий твои ответы, и удивительная система тестирования.
Обо всем по порядку расскажу тебе после быстрой регистрации.
Присоединиться к ExamMe
ЕГЭ по Математике (профильный)
Задание:
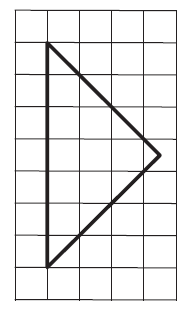
На клетчатой бумаге в размером 1 х 1 изображён равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведенной к гипотенузе.
Решение:
По условию, треугольник ABC является равнобедренным и прямоугольным, значит углы при основании равны и один угол равен 90 градусов. Мы знаем, что в треугольнике сумма углов равна 180 градусов, а т.к. один угол известен и составляет 90 градусов, то два других угла будут равны $180^{circ}-90^{circ}=90^{circ}$. Значит, углы при основании треугольника будут равны по $90^{circ}div 2=45^{circ}$.
Одно из свойств равнобедренного треугольника гласит — в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. В нашем случае НС является и медианой и биссектрисой, а значит делит прямой угол пополам.
По клеткам видно, что гипотенуза АВ = 7, значит медиана НС = $7div 2=3,5.$
Ответ:
3,5
Задание добавил(а)
О задание:
Источник условия: Книга: Подготовка к ЕГЭ. Диагностические работы. ЕГЭ 2017. Профильный уровень. Издательство: МЦНМО, 2017
Источник решения: Авторский коллектив ExamMe.RU
Обсуждения
Только зарегистрированные пользователи могут оставлять комментарии.
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найдите длину его медианы, проведенной к стороне ВС.
Источник задания: alexlarin.net
Решение:
Медиана будет делить сторону ВС на две равные части:
Медиану найдём из прямоугольного треугольника с катетами 3 и 4, это египетский треугольник гипотенуза будет равна 5. (можно найти и по теореме Пифагора)
Ответ: 5.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
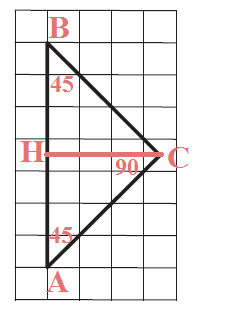
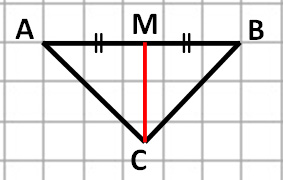
Задание. На клетчатой бумаге с размером клетки 1 × 1 изображен равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведенной к гипотенузе.
Решение:
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
Найдем середину стороны АВ и проведем отрезок СМ. Отрезок СМ – медиана треугольника АВС.
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине.
Длина гипотенузы АВ = 5, значит, СМ = 1/2АВ = 5/2 = 2,5
Ответ: 2,5