Как найти медиану ряда чисел пример - Исправление недочетов и поиск решений вместе с Examum.ru

Если в числовом ряде есть дробные числа, используйте точку для их записи. Например, 0.42, 0.55.

Медианой ряда
чисел (или медианой числового ряда) называется число, стоящее посередине
упорядоченного по возрастанию ряда чисел — в случае, если
количество чисел нечётное. Если же количество чисел в ряду чётно, то медианой ряда является полусумма двух стоящих
посередине чисел упорядоченного по возрастанию ряда.

Как найти медиану ряда чисел

Чтобы разобраться, как находить медиану ряда чисел, мы рассмотрим несколько примеров.

Пример 1. Найти медиану числового ряда

Решение. Записываем все числа ряда в порядке возрастания: . Количество чисел в ряду
чётно, поэтому медиана этого ряда будет равна полусумме двух средних чисел: $frac{5+9}{2}=7$ .

Пример 2. Найти медиану числового ряда

Решение. записываем все числа ряда в порядке возрастания: . Количество чисел в ряду
нечётно, поэтому медиана этого ряда будет равна стоящему посередине числу, то есть равна .

Источник

Медиана (x̃, M; Мера центральной тенденции) – это центральное значение Выборки (Sample).

В математике медиана также представляет собой тип Среднего значения (Average), который используется для нахождения «центра». Поэтому ее еще называют мерой центральной тенденции.

Нечетное количество элементов ряда

Если в ряду нечетное количество элементов, то мы сортируем значения в возрастающем или убывающем порядке, а затем выбираем центральное.

Пример. Найдем медиану следующего ряда:

4, 17, 77, 25, 22, 23, 92, 82, 40, 24, 14, 12, 67, 23, 29

Расставив эти числа по порядку, мы получим:

4, 12, 14, 17, 22, 23, 23, 24, 25, 29, 40, 67, 77, 82, 92

Всего пятнадцать элементов, то есть 8-й будет центральным. Медианное значение этого набора чисел – 24.

Четное количество элементов ряда

Если в ряду четное количество элементов, медиана рассчитывается с помощью формулы:

$$M = frac{n + 1}{2}, где$$
$$Mspace{–}space{медиана,}$$
$$nspace{–}space{количество}space{элементов}space{в}space{выборке}$$

Пример. Найдем медиану следующего ряда:

1.79, 1.61, 2.09, 1.84, 1.96, 2.11

Выполнив подстановку, мы получим:

$$M = frac{6 + 1}{2} = 3.5$$

Центральная тенденция

Помимо медианы, выделяют еще две другие меры центральной тенденции – Среднее значение (Mean) и Мода (Mode). Среднее – это частное от суммы всех Наблюдений (Observation) к их количеству. Мода – это наиболее часто повторяющееся значение выборки.

В Науке о данных (Data Science) медиана иногда используется вместо среднего значения, когда в последовательности есть выбросы, которые могут исказить среднее. Выбросы меньше влияют на медианное значение, чем на среднее. Медиана отделяет верхнюю половину выборки, генеральной совокупности или Распределения вероятностей (Probability Distribution) от нижней.

Медиана распределения вероятностей

Медиана и NumPy

Медиану можно вычислить с помощью NumPy. Для начала импортируем все необходимые библиотеки:

import numpy as np

Создадим массив из 6 элементов и вызовем встроенный метод median():

a = [10, 7, 4, 3, 2, 1]
np.median(a)

NumPy определяет четность числа элементов массива (6) и применяет тот или иной метод расчета (согласно формуле):

3.5

Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.

Фото: @garciasaldana_

Источник

Помимо моды, среднего арифметического и размаха ряда чисел существует также такое понятие, как медиана. Ее используют для того, чтобы охарактеризовать какой-либо числовой ряд. Медианой называют среднее число в представленном ряду, то есть то, которое будет стоять в его середине.

Медиана — это число, стоящее посередине упорядоченного по возрастанию ряда чисел (в случае, если количество чисел нечетное), или же полусумма двух стоящих в середине чисел (если количество чисел в ряду четное).

На письме медиану обозначают как $Me$.

Стоит отметить, что медиана и среднее арифметическое — это не одно и то же. В первом случае мы будем брать число из середины ряда, а во втором — среднее значение.

Рассмотрим на примере. Нам дан определенный числовой ряд, состоящий из $13$ значений:

$$-3, 0, 0, 0, 3, 4, textcolor{blue}{8}, 8, 8, 8, 12, 15, 100$$

В данном ряду все числа расставлены по возрастанию, поэтому из $13$ позиций нам нужно найти ту, которая будет стоять в центре ряда. Ей станет позиция под номером $7$. Если мы посмотрим на числовой ряд, то можем увидеть, что на седьмом месте стоит число $textcolor{blue}{8}$. Таким образом, мы нашли медиану данного числового ряда, а в ответе можем записать, что $Me=8$.

Алгоритм нахождения медианы

Искать медиану в числовом ряде достаточно просто, для этого достаточно всего лишь придерживаться определенного алгоритма:

Первым шагом будет нужно упорядочить числовой набор, выписав все числа последовательно в порядке возрастания.
Затем, чтобы было удобнее находить медиану, следует поочередно зачеркивать одновременно самое большое и самое маленькое числа, то есть одно значение из начала числового ряда, а другое — из его конца. Это нужно делать до тех пор, пока в середине не останется одно (если ряд имеет нечетное количество чисел) или два (если ряд имеет четного количества чисел) значения.
При условии, что в центре остается одно число, его и считают медианой, поэтому в таком случае задача уже будет решена.
Если же в середине осталось два числа, то нужно найти их полусумму. Полученное значение и будет являться медианой числового ряда.

Попробуем применить данный алгоритм на примере. У нас имеется следующий ряд чисел:

$$19, 7, 21, 2, 15, 5$$

Прежде всего запишем все числа в порядке возрастания друг за другом:

$$2, 5, 7, 15, 19, 21$$

Теперь начнем убирать самое большое и самое маленькое значения. Сначала зачеркиваем числа $21$ и $2$, затем $19$ и $5$. Мы видим, что в середине осталось два числа, так как числовой ряд состоял из четного количества чисел.

$$textcolor{red}{2}, textcolor{red}{5}, 7, 15, textcolor{red}{19}, textcolor{red}{21}$$

Чтобы найти медиану, нам нужно сложить числа $7$ и $15$, после чего разделить их на два. Получается такой пример:

$$frac{7+15}{2}=frac{22}{2}=11$$

Значение $11$ и будет являться искомой медианой, поэтому в ответе мы можем записать, что $Me=11$.

Источник

Понятие медианы чисел широко используется в математической статистике. И хотя вычисление медианы не составляет большой сложности, мы сделали калькулятор, который поможет рассчитать медианное значение ряда чисел онлайн с подробным решением. Причем количество чисел не важно, он рассчитает медиану 3, 4, 5 чисел так же быстро, как и для 1000 чисел.

Калькулятор медиана чисел

Как найти медиану чисел

Лучше рассмотреть процесс вычисления медианы на примере. Пусть у нас есть ряд чисел: 13 19 24 17 15 11. Для удобства числа будет записывать через пробел. Найдем его медиану. Для начала необходимо расположить числа в порядке возрастания. Эта процедура называется сортировкой. Получим новый ряд: 11 13 15 17 19 24. Так как количество чисел в ряду равно 6, а число 6 четное, то середина ряда будет между числами 15 и 17. Найдем среднее этих двух чисел: (15 + 17) / 2 = 16. Это и будет медианой ряда. Не стоит путать медиану, среднее гармоническое и среднее арифметическое — это принципиально разные понятия.

Рассмотрим другой пример, когда количество чисел в ряду нечетное. Есть такой ряд: 18 46 10 5 38. Найдем медиану набора этих чисел. Отсортируем ряд по возрастанию и получим ряд: 5 10 18 38 48. Так как количество чисел в этом ряду 5, то у него есть середина — это элемент с номером 2. Значит медиана этого ряда равна элементу с номером 2. Получаем ответ 18.

И еще пример — найдем медиану чисел 158 166 134 130 132. Отсортируем и получим ряд 130 132 134 158 166. Количество чисел нечетное и равно 5, значит средний элемент имеет номер 3. Третий элемент нашего отсортированного ряда — число 134. Это и есть медиана.

Ваша оценка

[Оценок: 263 Средняя: 3]

Медиана ряда чисел Автор admin средний рейтинг 3/5 — 263 рейтинги пользователей

Источник

В статистических исследованиях довольно широко применяются средние величины. Их нахождение позволяет выявить типичное значение признака исследуемой совокупности. Например, типичный уровень доходов покупателей или возраст большинства клиентов компании. При этом вычисление, к примеру, среднего арифметического не всегда уместно.

Представим такую ситуацию: мы опросили 10 человек на предмет их уровня доходов. У 9-х доходы оказались примерно одинаковыми и составили 10 тыс. руб. Что касается 10-ого опрошенного, то оказалось, что его доход равняется 410 тыс. руб. в месяц. Если мы вычислим простое среднее арифметическое, то типичный доход будет равняться 50 тыс. руб.! Но это явно не так. В таких ситуациях более объективную и правдоподобную картину дает вычисление моды или медианы, которые относятся к структурным средним показателям.

Понятие медианы

Медиана (Me) — значение признака в исследуемом ряду величин, которое делит этот ряд на две равные части.

То есть половина (50%) всех значений в исследуемом ряду будет меньше медианы, а другая половина — больше ее. Поэтому медиану еще называют 50-й перцентиль или квантиль 0,5.

Формула для расчета медианы

Если значений немного, то медиану можно определить «на глазок». Для этого достаточно расположить все значения в порядке возрастания и найти середину.

Если число случаев четное и в центре ряда находятся два разных числа, то медианой будет среднее между ними (даже если такого значения нет в самом ряду исследуемых случаев). Например, в ряду 1 2 3 4 5 6, медианой будет 3,5.

Для нахождения медианы в более сложных случаях (по интервальным рядам) используется специальная формула:

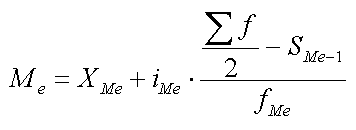
где: M_e — медиана;

X_me — нижняя граница медианного интервала (того интервала, накопленная частота которого превышает полусумму всех частот);

i_me — величина медианного интервала;

f — частота (сколько раз в ряду встречается то или иное значение);

S_me-1 — сумма частот интервалов предшествующих медианному интервалу;

f_me — число значений в медианном интервале (его частота).

Пример вычисления медианы

Был проведен опрос среди покупателей с целью выяснить их типичный возраст. По результатам опроса было установлено, что: 25 покупателей имеют возраст до 20 лет; 32 покупателя — 20-40 лет; 18 покупателей — 40-60 лет; 15 покупателей — свыше 60 лет. Найдем медиану.

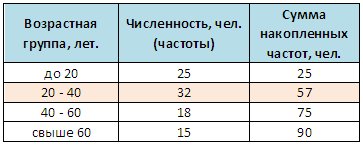
Сначала находим медианный интервал. Для этого вычисляем сумму частот: 25 + 32 + 18 + 15 = 90. Половина этой суммы — 45. Это соответствует возрастной группе 20-40 лет (т. к. полученная полусумма частот — 45, и накопленная частота 1-й группы меньше ее, а 3-ей — больше). Тогда нижняя граница медианного интервала — 20 (лет), а величина медианного интервала — 20 (40 лет за вычетом 20). Сумма частот интервалов предшествующих медианному интервалу — 25. Число значений в медианном интервале — 32 (количество покупателей в возрасте 20-40 лет).

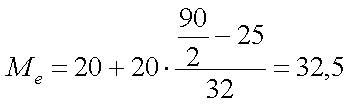
Расчетное значение медианы — 32,5. Округив его, получим средний возраст покупателя — 33 года.

Область применения медианы

При вычислении типичного признака неоднородных рядов, имеющих «выбросы» — значения во много раз отличающиеся от других значений ряда.

Особенности медианы

Медиана обладает высокой робастностью, то есть нечувствительностью к неоднородностям и ошибкам выборки;
Сумма разностей между членами ряда выборки и медианой меньше, чем сумма этих разностей с любой другой величиной. В том числе с арифметическим средним.

Источники

Медиана // Википедия. URL: http://ru.wikipedia.org/wiki/Медиана_(статистика) (дата обращения: 23.10.2013)
Минашкин В. Г. и др. Курс лекций по теории статистики. – М.: МЭСИ, 2001.

Нашли опечатку? Помогите сделать статью лучше! Выделите орфографическую ошибку мышью и нажмите Ctrl + Enter.

Библиографическая запись для цитирования статьи по ГОСТ Р 7.0.5-2008:
Галяутдинов Р.Р. Медиана // Сайт преподавателя экономики. [2013]. URL: https://galyautdinov.ru/post/mediana (дата обращения: 29.05.2023).

Источник