Как найти медиану ряда с четным количеством

Была ли эта статья полезной?

Формула медианы числового набора, пример вычисления медианы числового ряда: 3, 7, 1, 6, 9
Решение: упорядочиваем список чисел в порядке возрастания: 1, 3, 6, 7, 9. Поскольку количество чисел в ряду нечётное, то число 6 стоящее по середине и будет являться медианой данного ряда.

Пример нахождения медианы ряда чисел: 1, 5, 8, 4, 3, 9
Решение: записываем все числа ряда в порядке возрастания: 1, 3, 4 ,5, 8, 9. Поскольку чисел в ряду чётное, то медиана этого ряда будет равна полусумме двух средних чисел: (4+5)/2 = 4.5

В статистических исследованиях довольно широко применяются средние величины. Их нахождение позволяет выявить типичное значение признака исследуемой совокупности. Например, типичный уровень доходов покупателей или возраст большинства клиентов компании. При этом вычисление, к примеру, среднего арифметического не всегда уместно.

Представим такую ситуацию: мы опросили 10 человек на предмет их уровня доходов. У 9-х доходы оказались примерно одинаковыми и составили 10 тыс. руб. Что касается 10-ого опрошенного, то оказалось, что его доход равняется 410 тыс. руб. в месяц. Если мы вычислим простое среднее арифметическое, то типичный доход будет равняться 50 тыс. руб.! Но это явно не так. В таких ситуациях более объективную и правдоподобную картину дает вычисление моды или медианы, которые относятся к структурным средним показателям.

Понятие медианы

Медиана (Me) — значение признака в исследуемом ряду величин, которое делит этот ряд на две равные части.

То есть половина (50%) всех значений в исследуемом ряду будет меньше медианы, а другая половина — больше ее. Поэтому медиану еще называют 50-й перцентиль или квантиль 0,5.

Формула для расчета медианы

Если значений немного, то медиану можно определить «на глазок». Для этого достаточно расположить все значения в порядке возрастания и найти середину.

Если число случаев четное и в центре ряда находятся два разных числа, то медианой будет среднее между ними (даже если такого значения нет в самом ряду исследуемых случаев). Например, в ряду 1 2 3 4 5 6, медианой будет 3,5.

Для нахождения медианы в более сложных случаях (по интервальным рядам) используется специальная формула:

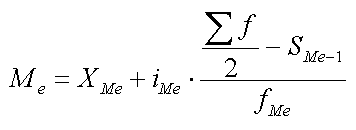
где: M_e — медиана;

X_me — нижняя граница медианного интервала (того интервала, накопленная частота которого превышает полусумму всех частот);

i_me — величина медианного интервала;

f — частота (сколько раз в ряду встречается то или иное значение);

S_me-1 — сумма частот интервалов предшествующих медианному интервалу;

f_me — число значений в медианном интервале (его частота).

Пример вычисления медианы

Был проведен опрос среди покупателей с целью выяснить их типичный возраст. По результатам опроса было установлено, что: 25 покупателей имеют возраст до 20 лет; 32 покупателя — 20-40 лет; 18 покупателей — 40-60 лет; 15 покупателей — свыше 60 лет. Найдем медиану.

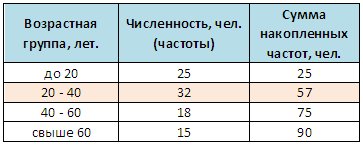
Сначала находим медианный интервал. Для этого вычисляем сумму частот: 25 + 32 + 18 + 15 = 90. Половина этой суммы — 45. Это соответствует возрастной группе 20-40 лет (т. к. полученная полусумма частот — 45, и накопленная частота 1-й группы меньше ее, а 3-ей — больше). Тогда нижняя граница медианного интервала — 20 (лет), а величина медианного интервала — 20 (40 лет за вычетом 20). Сумма частот интервалов предшествующих медианному интервалу — 25. Число значений в медианном интервале — 32 (количество покупателей в возрасте 20-40 лет).

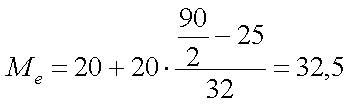
Расчетное значение медианы — 32,5. Округив его, получим средний возраст покупателя — 33 года.

Область применения медианы

При вычислении типичного признака неоднородных рядов, имеющих «выбросы» — значения во много раз отличающиеся от других значений ряда.

Особенности медианы

• Медиана обладает высокой робастностью, то есть нечувствительностью к неоднородностям и ошибкам выборки;
• Сумма разностей между членами ряда выборки и медианой меньше, чем сумма этих разностей с любой другой величиной. В том числе с арифметическим средним.

© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.

Нашли опечатку? Помогите сделать статью лучше! Выделите орфографическую ошибку мышью и нажмите Ctrl + Enter.

Библиографическая запись для цитирования статьи по ГОСТ Р 7.0.5-2008:
Галяутдинов Р.Р. Медиана // Сайт преподавателя экономики. [2013]. URL: https://galyautdinov.ru/post/mediana (дата обращения: 26.05.2023).

Золотая середина. Поиск медианного элемента потока входных чисел

В этой статье мы рассмотрим следующую задачу: поиск и поддержание медианы среди целых чисел, которые последовательно попадают на обработку. В этом посте мы поставим задачу, разберём все необходимые вводные, предложим и оценим сложность решения.

Постановка задачи

На вход алгоритму подаётся поток целых чисел, т.е. количество чисел может быть неизвестно, но мы будем считать, что массив задан наперёд и его длина очень большая. Требуется разработать алгоритм, который определяет медиану текущего массива, т.е. считанного из исходного к данному моменту. При этом требуется, чтобы сложность такого алгоритма была

Медиана ряда чисел

Начнём с базовых понятий. Медианой называется число, стоящее в упорядоченном ряде чисел посередине. Например в ряду: 1, 2, 3, 7, 9 — тройка является медианой. Если количество чисел чётное, то за медиану принимают среднее двух стоящих в центре чисел.

Либо можно выбирать элемент под номером , если чётное и если нечетное.

Наивный подход

Давайте обсудим бейзлайновое решение, при котором медиану можно получить за .

Пусть каждое новое число из потока мы будем вставлять в массив так, чтобы массив оставался упорядоченным. Затем будем выбирать элемент из середины и добавлять его в список медиан.

medians = []
items_read = []
with open('./Median.txt', 'r') as f:
    for line in f:
        num = int(line.strip())
        for idx in range(len(items_read)):
            if num < items_read[idx]:
                items_read.insert(idx, num)
                break
        if len(items_read) % 2 == 0:
            median_pos = len(items_read) // 2
        else:
            median_pos = len(items_read) + 1 // 2
        medians.append(median_pos)

Как упоминалось выше, этот алгоритм будет иметь квадратичную сложность, поскольку для каждого из элементов потока, мы выполняем линейную работу по поиску места и вставке элемента в массив.

Улучшить этот результат нам поможет структура данных — куча.

Куча. Min-heap, max-heap

Рассмотрим кучу на примере min-heap. Min-heap — это бинарное дерево, обладающее двумя следующими свойствами:

1. ключи любого узла этого дерева всегда меньше, чем ключи его двух дочерних узлов,
2. такое дерево является полным, т.е. у него должны быть заполнены все уровни, за исключением последнего.

Пример кучи (источник)

Аналогично образом задаётся max-heap, нужно заменить «меньше» на «больше» в первом свойстве.
При решении задачи мы хотим воспользоваться операциями, которые благодаря построению кучи, могут быть выполнены быстрее, чем за линейное время.

Первая из этих операций: взятие минимума (максимума) и удаление

Работая с кучей, операцию взятия минимума можно осуществить за константное время. Поскольку минимум всегда хранится в корне дерева, то узнать его значение не составляет труда. Если же мы хотим удалить минимум и назначить на его место следующий по величине элемент, то нам потребуется вызвать метод extract, чья временная сложность тоже меньше линейной и равна .

Метод extract внутри себя запускает следующий процесс: сначала элемент с самого последнего уровня ставится в корень дерева, затем на корне дерева стартует метод bubble_down, который уровень за уровнем (а таких всего в полном дереве) опускает новый корневой узел.
Код реализации на языке Python смотри ниже.

Вторая операция: добавление элемента

Чтобы добавить произвольный элемент в кучу требуется выставить новый элемент на правильное место, не утратив 2 свойства кучи. Для этого новый элемент добавляется на последний уровень, а затем методом bubble_up поднимается в сторону корня, пока над ним не окажется элемент меньший него или он не станет корнем. Сложность этой операции также равна

Код, в котором мы определим необходимую функциональность с возможностью определения min и max-heap:

class Heap(object):
    def __init__(self, array, type):
        super(Heap, self).__init__()
        self.type = type
        self.data = []
        self.heapify(array)
    
    def heapify(self, array):
        for item in array:
            self.insert(item)

    def bubble_down(self, array, index=0):
        left = 2 * index + 1 
        right = 2 * index + 2
        size = len(array)
        least = index
        if self.type == 'min':
            if left < size and array[left] < array[least]:
                least = left
            if right < size and array[right] < array[least]:
                least = right
            if least != index:
                tmp_val = array[least]
                array[least] = array[index]
                array[index] = tmp_val
                self.bubble_down(array, index=least)
        else:
            if left < size and array[left] > array[least]:
                least = left
            if  right < size and array[right] > array[least]:
                least = right
            if least != index:
                tmp_val = array[least]
                array[least] = array[index]
                array[index] = tmp_val
                self.bubble_down(array, index=least)
    
    def bubble_up(self, array, index):
        parent = (index - 1) // 2
        if self.type == 'min':
            if array[index] < array[parent] and parent >= 0:
                tmp_val = array[parent]
                array[parent] = array[index]
                array[index] = tmp_val
                self.bubble_up(array, index=parent)
        else:
            if array[index] > array[parent] and parent >= 0:
                tmp_val = array[parent]
                array[parent] = array[index]
                array[index] = tmp_val
                self.bubble_up(array, index=parent)

    def extract(self):
        root = self.data.pop(0)
        self.data.insert(0, self.data.pop(-1))
        self.bubble_down(self.data, 0)
        return root

    def insert(self, element):
        self.data.append(element)
        self.bubble_up(self.data, index=len(self.data)-1)

if __name__ == "__main__":
    a = [3,99,4,88,0,5,1,2]
    b = Heap(a, type='max')
    print(b.data)

Оптимальное решение

Теперь перейдем непосредственно к реализации алгоритма контроля медианы, основанном на использовании кучи. Мы будем использовать две кучи, одну минимальную, другую максимальную. Идея заключается в следующем: давайте разделим поток значений на верхнюю часть, содержащую большие значения и нижнюю, содержащую меньшие значения. Первую реализуем на основе min-heap, чтобы легко получать минимальный элемент, который лежит на разделе, а вторую на основе max-heap.

Всякий раз, когда мы читаем из потока очередное число, будем добавлять его в верхнюю часть, если оно больше наименьшего из этой половины и в нижнюю часть, если верно обратное. Затем, осуществив вставку, будем балансировать две части, чтобы они содержали по половине из введенных значений.

Код:

from heap import Heap


top_nums = Heap([], 'min')
bot_nums = Heap([], 'max')
medians = []
with open('./Median.txt', 'r') as f:
    for line in f:
        num = int(line.strip())
        if len(top_nums.data):
            top_smallest = top_nums.data[0]
            if num > top_smallest:
                top_nums.insert(num)
            else:
                bot_nums.insert(num)
        else:
            bot_nums.insert(num)
        while len(top_nums.data) > len(bot_nums.data):
            bot_nums.insert(top_nums.extract())
        while len(top_nums.data) + 1 < len(bot_nums.data):
            top_nums.insert(bot_nums.extract())
        medians.append(bot_nums.data[0])

Каждую итерацию внешнего цикла, мы делаем несколько шагов сложностью , посколько операции вставки и получения элемента из кучи ограничены этой сложностью. По этой причине итоговая сложность не превышает .

Заключение

В этой статье на примере задачи мы обсудили преимущества кучи по сравнению со списком. Познакомились с временной сложностью операций над этой структурой данных. Реализовали код этой структуры, необходимый для эффективного выполнения задачи по поиску медианного элемента в потоке чисел.

В преддверии старта курса «Алгоритмы и структуры данных» приглашаем всех желающих на бесплатный двухдневный интенсив по теме: Алгоритм сжатия данных — код Хаффмана.

• ЗАПИСАТЬСЯ НА ИНТЕНСИВ. ДЕНЬ 1
• ЗАПИСАТЬСЯ НА ИНТЕНСИВ. ДЕНЬ 2