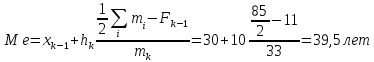Загрузить PDF
Загрузить PDF
Медиана — это среднее число в ряду или последовательности чисел. Когда речь идет о поиске медианы в последовательности, состоящей из нечетного количества полных чисел, процесс не представляет труда. Найти медиану в последовательности, где представлено четное количество полных чисел, будет несколько сложнее. Прочитайте нашу инструкцию, чтобы найти медиану легко и успешно.
-
1
Расположите числа от меньшего к большему.
- Если они перепутаны, расставьте их по порядку, начиная с меньшего и заканчивая большим.
-
2
Найдите число, стоящее ровно посередине. Это значит, что до медианы стоит столько же чисел, что и после медианы. Подсчитайте их, чтобы проверить.
- Перед числом 3 стоит два числа, после него — тоже два. Это значит, что 3 стоит в середине.
-
3
Вы закончили. Медиана в нечетном ряду чисел — это всегда одно из чисел множества. Медианой не может быть число, не входящее в числовой ряд.
Реклама
-
1
Расположите числа от меньшего к большему. Повторите первый шаг предыдущего метода. Четный ряд чисел будет содержать два числа ровно посередине.
-
2
Найдите среднее арифметическое чисел, стоящих в середине. 2 и 3 стоят в середине, поэтому надо к 2 прибавить 3 и разделить сумму на два. Формула вычисления среднего арифметического двух чисел: (сумма двух средних чисел)÷2
-
3
Вы закончили. Медиана ряда с четным количеством чисел не обязательно бывает одним из чисел ряда.
Реклама
Об этой статье
Эту страницу просматривали 25 473 раза.
Была ли эта статья полезной?
Медиана (x̃, M; Мера центральной тенденции) – это центральное значение Выборки (Sample).
В математике медиана также представляет собой тип Среднего значения (Average), который используется для нахождения «центра». Поэтому ее еще называют мерой центральной тенденции.
Нечетное количество элементов ряда
Если в ряду нечетное количество элементов, то мы сортируем значения в возрастающем или убывающем порядке, а затем выбираем центральное.
Пример. Найдем медиану следующего ряда:
4, 17, 77, 25, 22, 23, 92, 82, 40, 24, 14, 12, 67, 23, 29
Расставив эти числа по порядку, мы получим:
4, 12, 14, 17, 22, 23, 23, 24, 25, 29, 40, 67, 77, 82, 92
Всего пятнадцать элементов, то есть 8-й будет центральным. Медианное значение этого набора чисел – 24.
Четное количество элементов ряда
Если в ряду четное количество элементов, медиана рассчитывается с помощью формулы:
$$M = frac{n + 1}{2}, где$$
$$Mspace{–}space{медиана,}$$
$$nspace{–}space{количество}space{элементов}space{в}space{выборке}$$
Пример. Найдем медиану следующего ряда:
1.79, 1.61, 2.09, 1.84, 1.96, 2.11
Выполнив подстановку, мы получим:
$$M = frac{6 + 1}{2} = 3.5$$
Центральная тенденция
Помимо медианы, выделяют еще две другие меры центральной тенденции – Среднее значение (Mean) и Мода (Mode). Среднее – это частное от суммы всех Наблюдений (Observation) к их количеству. Мода – это наиболее часто повторяющееся значение выборки.
В Науке о данных (Data Science) медиана иногда используется вместо среднего значения, когда в последовательности есть выбросы, которые могут исказить среднее. Выбросы меньше влияют на медианное значение, чем на среднее. Медиана отделяет верхнюю половину выборки, генеральной совокупности или Распределения вероятностей (Probability Distribution) от нижней.
Медиана и NumPy
Медиану можно вычислить с помощью NumPy. Для начала импортируем все необходимые библиотеки:
import numpy as npСоздадим массив из 6 элементов и вызовем встроенный метод median():
a = [10, 7, 4, 3, 2, 1]
np.median(a)NumPy определяет четность числа элементов массива (6) и применяет тот или иной метод расчета (согласно формуле):
3.5Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Фото: @garciasaldana_
Среднее арифметическое, размах, мода и медиана
- Алгебра
- Среднее арифметическое, размах, мода и медиана
Статистические характеристики
количество чисел
Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда
чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите
рассчитать.
Среднее арифметическое, размах, мода и медиана
Средним арифметическим ряда чисел называется частное от деления суммы этих
чисел на число слагаемых.
Для ряда a1,a1,..,an среднее арифметическое вычисляется по
формуле:
begin{align}
& overline{a}=frac{a_1+a_2+…+a_n}{n}\
end{align}
Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.
begin{align}
& overline{a}=frac{5,24+6,97+8,56+7,32+6,23}{5}=6.864\
end{align}
Размахом ряда чисел называется разность между наибольшим и наименьшим из
этих чисел.
Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32
Модой ряда чисел называется число, которое встречается в данном ряду чаще
других.
Ряд чисел может иметь более одной моды, а может не иметь моды совсем.
Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.
В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.
Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.
Медианой упорядоченного ряда чисел с нечётным числом членов называется
число, записанное посередине, а медианой упорядоченного ряда чисел с чётным
числом членов называется среднее арифметическое двух чисел, записанных посередине.
Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного
ряда.
Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.
Примеры
Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды
ряда.
-
Среднее арифметическое чисел 30, 5, 23, 5, 28, 30
begin{align}
& overline{a}=frac{30+5+23+5+28+30}{6}=20frac{1}{6}\
end{align}Размах ряда: 30-5=25
Моды ряда: 5 и 30
Медиана ряда: 25.5
-
Среднее арифметическое чисел 40, 35, 30, 25, 30, 35
begin{align}
& overline{a}=frac{40+35+30+25+30+35}{6}=32frac{1}{2}\
end{align}Размах ряда: 40-25=15
Моды ряда: 30, 35
Медиана ряда: 32.5
-
Среднее арифметическое чисел 21, 18,5, 25,3, 18,5, 17,9
begin{align}
& overline{a}=frac{21+18,5+25,3+18,5+17,9}{5}=20,24\
end{align}Размах ряда: 25,3-17,9=7,4
Мода ряда: 18,5
Медиана ряда: 18,5
Примеры
Примеры нахождения среднего арифметического отрицательных и вещественных чисел.
-
Среднее арифметическое чисел 67,1, 68,2, 67,1, 70,4, 68,2
begin{align}
& overline{a}=frac{67,1+68,2+67,1+70,4+68,2}{5}=68,2\
end{align}Размах ряда: 70,4-67,1=3,3
Моды ряда: 67.1, 68.2
Медиана ряда: 68.2
-
Среднее арифметическое чисел 0,6, 0,8, 0,5, 0,9, 1,1
begin{align}
& overline{a}=frac{0,6+0,8+0,5+0,9+1,1}{5}=0.78\
end{align}Размах ряда: 1,1-0,5=0.6
Ряд не имеет моды
Медиана ряда: 0.8
-
Среднее арифметическое чисел -21, -33, -35, -19, -20, -22
begin{align}
& overline{a}=frac{(-21)+(-33)+(-35)+(-19)+(-20)+(-22)}{6}=-25\
end{align}Размах ряда: (-19)-(-35)=16
Ряд не имеет моды
Медиана ряда: -21,5
-
Среднее арифметическое чисел -4, -6, 0, -4, 0, 6, 8, -12
begin{align}
& overline{a}=frac{(-4)+(-6)+0+(-4)+0+6+8+(-12)}{8}=-1,5\
end{align}Размах ряда: 8-(-12)=20
Моды ряда: -4, 0
Медиана ряда: -2
-
Среднее арифметическое чисел 275, 286, 250, 290, 296, 315, 325
begin{align}
& overline{a}=frac{275+286+250+290+296+315+325}{7}=291\
end{align}Размах ряда: 325-250=75
Ряд не имеет моды
Медиана ряда: 290
-
Среднее арифметическое чисел 38, 42, 36, 45, 48, 45, 45, 42, 40, 47, 39
begin{align}
& overline{a}=frac{38+42+36+45+48+45+45+42+40+47+39}{11}=42frac{6}{11}\
end{align}Размах ряда: 48-36=12
Мода ряда: 45
Медиана ряда: 42
-
Среднее арифметическое чисел 3,8, 7,2, 6,4, 6,8, 7,2
begin{align}
& overline{a}=frac{3,8+7,2+6,4+6,8+7,2}{5}=6,28\
end{align}Размах ряда: 7,2-3,8=3,4
Мода ряда: 7,2
Медиана ряда: 6,8
-
Среднее арифметическое чисел 21,6, 37,3, 16,4, 12,6
begin{align}
& overline{a}=frac{21,6+37,3+16,4+12,6}{4}=21,025\
end{align}Размах ряда: 37,3-12,6=24,7
Мода ряда: 12,6
Медиана ряда: 17,1
-
Медиана
Медианой
(Me)
называется значение признака, которое
лежит в середине ранжированного ряда.
Ранжированный
ряд
– ряд, расположенный в порядке возрастания
или убывания значений признака.
В
дискретном ряду медиана находится на
основе накопленных частот. Номер медианы
равен половине суммы всех частот. Частоты
накапливаются до тех пор, пока не будет
превзойдён номер медианы. Медиана
равняется частоте, соответствующей
номеру медианы.
В
интервальном ряду сначала находится
медианный интервал. Номер медианы равен
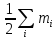

По номеру определяется интервал, которому
этот номер принадлежит. Затем медиана
определяется по формуле:
где
xk-1
– нижняя граница медианного интервала;
hk
– длина медианного интервала;
Fk-1
–
накопленная частота интервала,
предшествующему медианному;
mk
–
частота медианного интервала;
Pk-1
– накопленная частость интервала,
предшествующему медианному.
Если
требуется найти медиану в ранжированном
ряду без частот, то номер медианы можно
определить по формуле (N+1)/2,
если ряд содержит нечётное число
элементов. Затем по номеру медианы
выбирается медиана из значений признака.
Если ряд содержит четное число элементов,
то медиана вычисляется по формуле:
где
N
– число элементов в ряду.
В
интервальном ряду медиана определяется
по кумуляте. Для этого из точки на шкале
накопленных частот (частостей),
соответствующей

проводится прямая, параллельная оси
абсцисс до пересечения с кумулятой.
Затем на ось абсцисс опускается
перпендикуляр. Абсцисса точки пересечения
является медианой.
Пример 15.
Вычисление
медианы для дискретного вариационного
ряда
Найти
медиану для распределения сотрудников
по тарифным разрядам.
|
Тарифный |
Число |
Накопленная |
|
2 |
11 |
11 |
|
3 |
18 |
29 |
|
4 |
22 |
51 |
|
5 |
20 |
71 |
|
6 |
14 |
85 |
|
Итого |
85 |
Ряд
является дискретным. Номер медианы
равен 42 или 43 (85/2). Накапливать частоты
нужно до тех пор, пока не будет превзойдён
номер медианы: 11 сотрудников имеют не
более, чем 2 разряд; 29 сотрудников имею
не более, 3 разряд; 51 сотрудник имеет не
более, чем 4 разряд. Т.е. число сотрудников
42 и 43 приходится на 4 разряд. Следовательно,
Me=4.
Пример 16.
Вычисление
медианы для интервального вариационного
ряда с равной длиной интервалов
Найти
медиану для распределения сотрудников
по возрастам.
|
Возрастные |
Число |
Накоплен- ные |
Частости |
Накопленные |
||
|
в |
в |
в |
в |
|||
|
20 – |
11 |
11 |
0,1294 |
12,94 |
0,1294 |
12,94 |
|
30 – |
33 |
44 |
0,3882 |
38,82 |
0,5176 |
51,76 |
|
40 – |
22 |
66 |
0,2588 |
25,88 |
0,7764 |
77,64 |
|
50 – |
15 |
81 |
0,1765 |
17,65 |
0,9529 |
95,29 |
|
60 – |
4 |
85 |
0,0471 |
4,71 |
1 |
100 |
|
Итого |
85 |
1 |
100 |
Ряд
является интервальным. Номер медианы,
рассчитанный на основе накопленных
частот, равен 42 или 43 (85/2), а накопленный
на основе частостей равен 50 (100/2). На
основе накопленных частот определяется,
что числу сотрудников 42 и 43 соответствует
возрастной интервал 30 – 40. Далее находится
медиана:
Графическое
определение медианы:
Пример 17.
Вычисление
медианы ранжированного ряда с нечетным
числом интервалов
Найти
медиану для ранжированного ряда, в
котором представлены набранные баллы
участников конкурса.
|
Место |
Фамилия |
Баллы |
|
1 |
Иванов |
135 |
|
2 |
Смирнов |
117 |
|
3 |
Петров |
98 |
|
4 |
Сидоров |
89 |
|
5 |
Фёдоров |
64 |
|
6 |
Макаров |
57 |
|
7 |
Казаков |
53 |
В
таблице нечётное число элементов. Номер
медианы равен ((7+1)/2)=4. Этому номеру
соответствует медиана Me
= 89 баллов.
Пример 18.
Вычисление
медианы ранжированного ряда с нечетным
числом интервалов
Найти
медиану для ранжированного ряда, в
котором представлены набранные баллы
участников конкурса.
|
Место |
Фамилия |
Баллы |
|
1 |
Иванов |
135 |
|
2 |
Смирнов |
117 |
|
3 |
Петров |
98 |
|
4 |
Сидоров |
89 |
|
5 |
Фёдоров |
64 |
|
6 |
Макаров |
7 |
В
таблице чётное число элементов. Медиана
вычисляется по формуле:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
28 октября 2021 г.
{(n ÷ 2)-е значение + [(n ÷ 2) + 1]th value} ÷ 2 = медиана
Статистики и аналитики данных используют множество вычислений для организации, контекстуализации и интерпретации информации в своей работе. Одним из важных значений, которое эти профессионалы обычно определяют, является медиана. Если вы работаете со статистикой или данными или используете метрики на работе, может быть полезно понять, как найти медианное число. В этой статье мы определяем медиану, описываем формулу ее расчета, сравниваем медиану со средним и приводим примеры расчета медианы.
Что такое медиана?
Медиана — это среднее значение набора данных, когда вы упорядочиваете значения. Наряду со средним значением и модой это одна из центральных тенденций в наборе данных или числа, которые наиболее репрезентативны для тенденций в данных. Медиану иногда называют позиционным средним значением, что означает, что 50 % данных находятся выше медианы, а 50 % — ниже нее.
Медиана, среднее и мода
Медиана, среднее значение и мода — три важных числа, которые могут помочь аналитикам данных и статистикам обобщить тенденции в наборе данных. В то время как медиана — это среднее число в наборе данных, среднее — это результат сложения всех значений в наборе данных и их деления на количество элементов, включенных в набор. Мода — еще одна распространенная мера, которая относится к наиболее распространенному значению в наборе данных.
Почему важна медиана?
Медиана набора данных важна, потому что она может суммировать данные в одно число для репрезентативных целей. Хотя многие аналитики используют среднее значение для выявления важных тенденций в данных, иногда среднее значение может быть более полезным. Поскольку среднее значение включает все значения в наборе данных, очень высокие или низкие значения могут искажать важные тенденции. В этих случаях многие профессионалы находят медиану, потому что на нее не влияют выбросы.
Вычисление медианы
Для нахождения медианы в нечетных и четных наборах чисел необходимы разные вычисления. Вы можете использовать эти вычисления, чтобы найти медиану в наборе данных:
Для нечетного набора чисел
Нечетное число — это число, которое нельзя разделить на два, например, пять, семь или 17. Если в наборе данных есть нечетное количество значений, вы можете сначала расположить значения в порядке возрастания или убывания и использовать эту формулу, чтобы найти положение среднего:
Медиана = (n + 1) ÷ 2
В этом уравнении n представляет количество значений в наборе данных. Чтобы найти положение медианы, вы можете добавить единицу к количеству значений в наборе и разделить результат на два. Например, если результат этой формулы равен восьми, медиана — это восьмое число в последовательности. Если у вас есть небольшое количество точек данных, вы можете просто расположить их в порядке возрастания или убывания и найти средний номер.
Для четного набора чисел
Четные числа — это числа, которые можно разделить на два. Если у вас есть набор данных с четным количеством точек данных, вы можете сначала расположить их в порядке возрастания или убывания. Поскольку среднего числа нет, вам потребуются два средних числа последовательности, которые вы можете найти с помощью этих уравнений, в которых n — количество точек данных в наборе:
п ÷ 2
(n ÷ 2) + 1
Результатом этих уравнений являются положения двух средних точек в наборе данных. Например, если результаты равны восьми и девяти, вы можете искать восьмое и девятое числа в упорядоченной последовательности. Чтобы найти медиану, вы можете сложить два средних числа и разделить результат на два. Вы можете представить всю формулу с помощью этого уравнения:
{(n ÷ 2)-е значение + [(n ÷ 2) + 1]th value} ÷ 2 = медиана
Чему равна медиана двух чисел?
Чтобы найти медиану двух чисел, вы можете сложить их вместе и разделить результат на два. Вы можете представить эту формулу следующим уравнением, в котором x представляет первое число, а y представляет второе число:
(x + y) ÷ 2 = медиана
Например, если вы хотите найти медиану четырех и пяти, вы можете использовать этот расчет:
4 + 5 = 9
9 ÷ 2 = 4,5
Это означает, что медиана четырех и пяти равна 4,5.
Примеры расчета медианы
Вот несколько примеров того, как можно вычислить медиану различных наборов данных:
Пример расчета медианы для нечетного набора чисел
Это пример того, как вы можете вычислить среднее значение нечетного набора чисел:
Карла хочет определить среднюю почасовую заработную плату в ресторанах своего района. После сбора информации о девяти ресторанах у нее есть набор данных, включающий 15, 13.50, 14, 17, 11.50, 12, 11, 12.75 и 14.50. Во-первых, она может расположить числа в порядке значимости от наименьшего к наибольшему:
11, 11.50, 12, 12.75, 13.50, 14, 14.50, 15, 17
Поскольку у нее девять чисел, она использует это уравнение, чтобы найти положение среднего значения:
(9 + 1) ÷ 2 = 5
Это означает, что медиана в ее наборе данных — это пятое значение, которое составляет 13,50 долларов в час.
Пример расчета медианы для четного набора чисел
Вот пример того, как можно вычислить медиану четного набора чисел:
.Джон хочет найти среднее число братьев и сестер среди его группы из восьми друзей. После сбора информации от них у него есть список чисел, который включает пять, два, восемь, один, три, один, четыре и шесть. Во-первых, он упорядочивает числа в порядке значимости от наименьшего к наибольшему:
1, 1, 2, 3, 4, 5, 6, 8
Поскольку в его последовательности восемь чисел, он может использовать это уравнение, чтобы найти положение двух средних значений:
8 ÷ 2 = 4
(8 ÷ 2) + 1 = 5
Это означает, что два средних значения — это четвертое и пятое числа, то есть три и четыре в последовательности. Затем он может использовать этот расчет, чтобы найти среднее значение:
(3 + 4) ÷ 2 = 3,5
Это означает, что медиана его набора данных составляет 3,5 брата и сестры.
Пример медианы по сравнению со средним и модой
Это пример того, как вы можете определить и сравнить среднее значение, медиану и моду набора данных:
Лили пытается найти основные тенденции набора данных, включающего следующие 11 чисел:
23, 33, 67, 11, 24, 88, 54, 32, 43, 15, 11
Чтобы найти медиану, она упорядочивает числа, чтобы получить следующую последовательность:
11, 11, 15, 23, 24, 32, 33, 43, 54, 67, 88
Затем она может использовать это уравнение, чтобы найти медиану:
(11 + 1) ÷ 2 = 6
Это означает, что медиана — это шестое число, или 32.
Чтобы найти среднее значение, она использует это уравнение:
(11 + 11 + 15 + 23 + 24 + 32 + 33 + 43 + 54 + 67 + 88) ÷ 11 = 36,45
Это означает, что среднее или среднее значение набора данных равно 36,45.
Чтобы найти моду, она может просто искать число, которое встречается чаще всего. Поскольку только 11 появляется дважды, это режим набора данных.