Как найти медиану списка чисел

Sometimes, while working with Python list we can have a problem in which we need to find Median of list. This problem is quite common in the mathematical domains and generic calculations. Let’s discuss certain ways in which this task can be performed.
 Method #1 : Using loop + “~” operator This task can be performed in brute force manner using the combination of above functionalities. In this, we sort the list and the by using the property of “~” operator to perform negation, we access the list from front and rear, performing the required computation required for finding median. 

The original list : [4, 5, 8, 9, 10, 17]
Median of list is : 8.5

Time Complexity: O(n) where n is the number of elements in the list “test_list”. loop + “~” operator performs n number of operations.
Auxiliary Space: O(1), constant extra space is required.

  Method #2 : Using statistics.median() This is the most generic method to perform this task. In this we directly use inbuilt function to perform the median of the list. 

The original list : [4, 5, 8, 9, 10, 17]
Median of list is : 8.5

Using python heapq.nlargest() or heapq.nsmallest()

Explanation: Using python’s heapq module, we can use the nlargest() or nsmallest() function to find the median of a list of numbers. This method is useful when we are working with large amount of data and we want to find median of large dataset with minimum memory footprint.

The original list : [4, 5, 8, 9, 10, 17]
Median of list is : 8.5

Time complexity: O(n log(k)) where k = len(test_list)/2
Auxiliary Space: O(k) where k = len(test_list)/2

Method  : Using sort the list:

The original list : [4, 5, 8, 9, 10, 17]
Median of list is : 8.5

Time complexity: O(n log n)
Auxiliary Space: O(n) 

Last Updated :
12 Apr, 2023

Like Article

Save Article

Мой любимый алгоритм: нахождение медианы за линейное время

Нахождение медианы списка может казаться тривиальной задачей, но её выполнение за линейное время требует серьёзного подхода. В этом посте я расскажу об одном из самых любимых мной алгоритмов — нахождении медианы списка за детерминированное линейное время с помощью медианы медиан. Хотя доказательство того, что этот алгоритм выполняется за линейное время, довольно сложно, сам пост будет понятен и читателям с начальным уровнем знаний об анализе алгоритмов.

Нахождение медианы за O(n log n)

Самым прямолинейным способом нахождения медианы является сортировка списка и выбор медианы по её индексу. Самая быстрая сортировка сравнением выполняется за O(n log n), поэтому от неё зависит время выполнения¹, ².

def nlogn_median(l):
    l = sorted(l)
    if len(l) % 2 == 1:
        return l[len(l) / 2]
    else:
        return 0.5 * (l[len(l) / 2 - 1] + l[len(l) / 2])

У этого способа самый простой код, но он определённо не самый быстрый.

Нахождение медианы за среднее время O(n)

Следующим нашим шагом будет нахождение медианы в среднем за линейное время, если нам будет везти. Этот алгоритм, называемый «quickselect», разработан Тони Хоаром, который также изобрёл алгоритм сортировки с похожим названием — quicksort. Это рекурсивный алгоритм, и он может находить любой элемент (не только медиану).

1. Выберем индекс списка. Способ выбора не важен, на практике вполне подходит и случайный. Элемент с этим индексом называется опорным элементом (pivot).
2. Разделим список на две группы:
   1. Элементы меньше или равные pivot, lesser_els
   2. Элементы строго большие, чем pivot, great_els
3. Мы знаем, что одна из этих групп содержит медиану. Предположим, что мы ищем k-тый элемент:
   • Если в lesser_els есть k или больше элементов, рекурсивно обходим список lesser_els в поисках k-того элемента.
   • Если в lesser_els меньше, чем k элементтов, рекурсивно обходим список greater_els. Вместо поиска k мы ищем k-len(lesser_els).

Вот пример алгоритма, выполняемого для 11 элементов:

Возьмём представленный ниже список. Мы хотим найти медиану.
l = [9,1,0,2,3,4,6,8,7,10,5]
len(l) == 11, поэтому мы ищем шестой наименьший элемент 
Сначала нам нужно выбрать опорный элемент (pivot). Мы случайным образом выбираем индекс 3. 
Значение элемента с этим индексом равно 2.

Разбиваем список на группы согласно pivot:
[1,0,2], [9,3,4,6,8,7,10,5]
Нам нужен шестой элемент. 6-len(left) = 3, поэтому нам нужен
третий наименьший элемент в правом массиве 

Теперь мы ищем третий наименьший элемент в следующем массиве:
[9,3,4,6,8,7,10,5]
Мы случайным образом выбираем индекс, который будет нашим pivot. 
Мы выбрали индекс 2, значение в котором равно l[2]=6

Разбиваем на группы согласно pivot:
[3,4,5,6] [9,7,10]
Нам нужен третий наименьший элемент, поэтому мы знаем, что это
третий наименьший элемент в левом массиве

Теперь мы ищем третий наименьший в следующем массиве:
[3,4,5,6]
Мы случайным образом выбираем индекс, который будет нашим pivot.
Мы выбрали индекс 1, значение в котором равно l[1]=4
Разбиваем на группы согласно pivot:
[3,4] [5,6]
Нам нужен третий наименьший элемент, поэтому мы знаем, что это
наименьший элемент в правом массиве.

Теперь мы ищем наименьший элемент в следующем массиве:
[5,6]

На этом этапе у нас есть базовый вариант, выбирающий наибольший
или наименьший элемент на основании индекса.
Нам нужен наименьший элемент, то есть 5.
return 5

Чтобы найти с помощью quickselect медиану, мы выделим quickselect в отдельную функцию. Наша функция quickselect_median будет вызывать quickselect с нужными индексами.

import random
def quickselect_median(l, pivot_fn=random.choice):
    if len(l) % 2 == 1:
        return quickselect(l, len(l) / 2, pivot_fn)
    else:
        return 0.5 * (quickselect(l, len(l) / 2 - 1, pivot_fn) +
                      quickselect(l, len(l) / 2, pivot_fn))


def quickselect(l, k, pivot_fn):
    """
    Выбираем k-тый элемент в списке l (с нулевой базой)
    :param l: список числовых данных
    :param k: индекс
    :param pivot_fn: функция выбора pivot, по умолчанию выбирает случайно
    :return: k-тый элемент l
    """
    if len(l) == 1:
        assert k == 0
        return l[0]

    pivot = pivot_fn(l)

    lows = [el for el in l if el < pivot]
    highs = [el for el in l if el > pivot]
    pivots = [el for el in l if el == pivot]

    if k < len(lows):
        return quickselect(lows, k, pivot_fn)
    elif k < len(lows) + len(pivots):
        # Нам повезло и мы угадали медиану
        return pivots[0]
    else:
        return quickselect(highs, k - len(lows) - len(pivots), pivot_fn)

В реальном мире Quickselect отлично себя проявляет: он почти не потребляет лишних ресурсов и выполняется в среднем за O(n). Давайте докажем это.

Доказательство среднего времени O(n)

В среднем pivot разбивает список на две приблизительно равных части. Поэтому каждая последующая рекурсия оперирует с ¹⁄₂ данных предыдущего шага.

Существует множество способов доказательства того, что этот ряд сходится к 2n. Вместо того, чтобы приводить их здесь, я сошлюсь на замечательную статью в Википедии, посвящённую этому бесконечному ряду.

Quickselect даёт нам линейную скорость, но только в среднем случае. Что, если нас не устраивает среднее, и мы хотим гарантированного выполнения алгоритма за линейное время?

Детерминированное O(n)

В предыдущем разделе я описал quickselect, алгоритм со средней скоростью O(n). «Среднее» в этом контексте означает, что в среднем алгоритм будет выполняться за O(n). С технической точки зрения, нам может очень не повезти: на каждом шаге мы можем выбирать в качестве pivot наибольший элемент. На каждом этапе мы сможем избавляться от одного элемента из списка, и в результате получим скорость O(n^2), а не O(n).

С учётом этого, нам нужен алгоритм для подбора опорных элементов. Нашей целью будет выбор за линейное время pivot, который в худшем случае удаляет достаточное количество элементов для обеспечения скорости O(n) при использовании его вместе с quickselect. Этот алгоритм был разработан в 1973 году Блумом (Blum), Флойдом (Floyd), Праттом (Pratt), Ривестом (Rivest) и Тарьяном (Tarjan). Если моего объяснения вам не хватит, то можете изучить их статью 1973 года. Вместо того, чтобы описывать алгоритм, я подробно прокомментирую мою реализацию на Python:

def pick_pivot(l):
    """
    Выбираем хорошй pivot в списке чисел l
    Этот алгоритм выполняется за время O(n).
    """
    assert len(l) > 0

    # Если элементов < 5, просто возвращаем медиану
    if len(l) < 5:
        # В этом случае мы возвращаемся к первой написанной нами функции медианы. 
        # Поскольку мы выполняем её только для списка из пяти или менее элементов, она не 
        # зависит от длины входных данных и может считаться постоянным
        # временем.
        return nlogn_median(l)

    # Сначала разделим l на группы по 5 элементов. O(n)
    chunks = chunked(l, 5)

    # Для простоты мы можем отбросить все группы, которые не являются полными. O(n)
    full_chunks = [chunk for chunk in chunks if len(chunk) == 5]


    # Затем мы сортируем каждый фрагмент. Каждая группа имеет фиксированную длину, поэтому каждая сортировка
    # занимает постоянное время. Поскольку у нас есть n/5 фрагментов, эта операция 
    # тоже O(n)
    sorted_groups = [sorted(chunk) for chunk in full_chunks]

    # Медиана каждого фрагмента имеет индекс 2
    medians = [chunk[2] for chunk in sorted_groups]

    # Возможно, я немного повторюсь, но я собираюсь доказать, что нахождение
    # медианы списка можно произвести за доказуемое O(n).
    # Мы находим медиану списка длиной n/5, поэтому эта операция также O(n)
    # Мы передаём нашу текущую функцию pick_pivot в качестве создателя pivot алгоритму
    # quickselect. O(n)
    median_of_medians = quickselect_median(medians, pick_pivot)
    return median_of_medians

def chunked(l, chunk_size):
    """Разделяем список `l` на фрагменты размером `chunk_size`."""
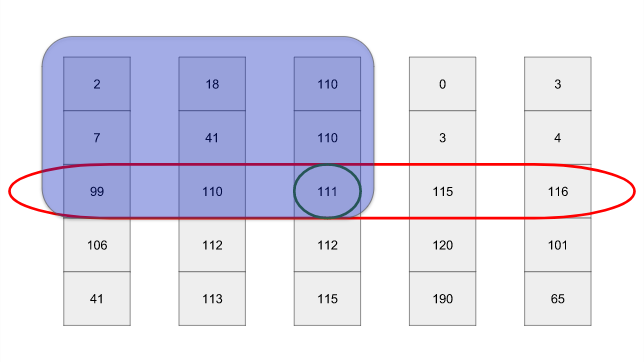
    return [l[i:i + chunk_size] for i in range(0, len(l), chunk_size)]

Давайте докажем, что медиана медиан является хорошим pivot. Нам поможет, если мы представим визуализацию нашего алгоритма выбора опорных элементов:

Красным овалом обозначены медианы фрагментов, а центральным кругом — медиана медиан. Не забывайте, мы хотим, чтобы pivot разделял список как можно ровнее. В худшем возможном случае каждый элемент в синем прямоугольнике (слева вверху) будет меньше или равен pivot. Верхний правый прямоугольник содержит ³⁄₅ половины строк — 3/5*1/2=3/10. Поэтому на каждом этапе мы избавляемся по крайней мере от 30% строк.

Но достаточно ли нам отбрасывать 30% элементов на каждом этапе? На каждом этапе наш алгоритм должен выполнять следующее:

• Выполнять работу O(n) по разбиению элементов
• Для рекурсии решать одну подзадачу размером в ⁷⁄₁₀ от исходной
• Для вычисления медианы медиан решать одну подзадачу размером с ¹⁄₅ от исходной

В результате мы получаем следующее уравнение полного времени выполнения T(n):

Не так уж просто доказать, почему это равно O(n). Быстрое решение заключается в том, чтобы положиться на основную теорему о рекуррентных соотношениях. Мы попадаем в третий случай теоремы, при котором работа на каждом уровне доминирует над работой подзадач. В этом случае общая работа будет просто равна работе на каждом уровне, то есть O(n).

Подводим итог

У нас есть quickselect, алгоритм, который находит медиану за линейное время при условии наличия достаточно хорошей опорного элемента. У нас есть алгоритм медианы медиан, алгоритм O(n) для выбора опорного элемента (который достаточно хорош для quickselect). Соединив их, мы получили алгоритм нахождения медианы (или n-ного элемента в списка) за линейное время!

Медианы за линейное время на практике

В реальном мире почти всегда достаточно случайного выбора медианы. Хотя подход с медианой медиан всё равно выполняется за линейное время, на практике его вычисление длится слишком долго. В стандартной библиотеке C++ используется алгоритм под названием introselect, в котором применено сочетание heapselect и quickselect; предел его выполнения O(n log n). Introselect позволяет использовать обычно быстрый алгоритм с плохим верхним пределом в сочетании с алгоритмом, который медленнее на практике, но имеет хороший верхний предел. Реализации начинают с быстрого алгоритма, но возвращаются к более медленному, если не могут выбрать эффективные опорные элементы.

В завершение приведу сравнение элементов, используемых в каждой из реализаций. Это не скорость выполнения, а общее количество элементов, которые рассматривает функция quickselect. Здесь не учитывается работа по вычислению медианы медиан.

Именно этого мы и ожидали! Детерминированный опорный элемент почти всегда рассматривает при quickselect меньшее количество элементов, чем случайный. Иногда нам везёт и мы угадываем pivot с первой попытки, что проявляется как впадины на зелёной линии. Математика работает!

1. Это может стать интересным применением поразрядной сортировки (radix sort), если вам нужно найти медиану в списке целых чисел, каждое из которых меньше 2³².
2. На самом деле в Python используется Timsort, впечатляющее сочетание теоретических пределов и практической скорости. Заметки о списках в Python.