Как найти медиану треугольника зная координаты вершин

Помогите доказать методом координат. Самостоятельная работа 4. Вариант 7. № 1 ГДЗ Геометрия 9 класс Зив Б.Г. – Рамблер/класс

Помогите доказать методом координат. Самостоятельная работа 4. Вариант 7. № 1 ГДЗ Геометрия 9 класс Зив Б.Г. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Докажите методом координат, что медианы треугольника

пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершин треугольника.

ответы

Пусть А(0; 0), В(b; h), С(а; 0). Пусть BE медиана и

 Рассмотрим медиану АF и точку М₁ на ней такую, что

 => М и  М₁ совпадают. Аналогично и с медианой CG. Ч.т.д.

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

похожие вопросы 5

Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.

Привет. Запуталась при решении, нужна помощь знатоков!!!

 Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)

ГДЗГеометрия11 класс10 классАтанасян Л.С.

Самостоятельная работа 19.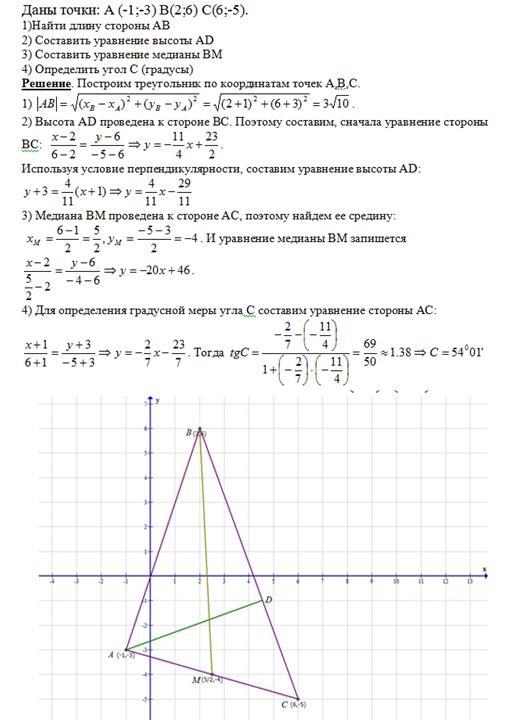 Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос

Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.

 

ГДЗЭкзаменыГеометрия9 классЗив Б. Г.

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Дадут ли аттестат после второй пересдачи.?

 Мне сказала подруга,что аттестат не дадут после второй пересдачи,дадут только справку и всё,так ли это?

9 класс

Ребята нужны ответы на пересдачу по математике 9 класс 11 регион. Срочно!

ГИА9 класс

Как найти медиану треугольника зная его стороны.

Медиана

Медиана и высота треугольника – это одна из самых увлекательных и интересных тем геометрии. Термин «Медиана» означает прямую или отрезок, который соединяет вершину треугольника с его противоположной стороной. Другими словами, медиана – это линия, которая проходит из середины одной стороны треугольника в противоположную вершину этого же треугольника. Поскольку у треугольника только три вершины и три стороны, значит и медианы может быть только три.

Свойства медианы треугольника

1. Все медианы треугольника пересекаются в одной точке и разделяются этой точкой в соотношении 2:1, считая от вершины. Таким образом, если нарисовать в треугольнике все три медианы, то точка их пересечения будет делить их на две части. Часть, которая располагается ближе в вершине, будет составлять 2/3 всей линии, а часть, которая располагается ближе к стороне треугольника – 1/3 линии. Пересекаются медианы в одной точке.
2. Три медианы, проведенные в одном треугольнике, делят этот треугольник на 6 маленьких треугольников, чья площадь будет равна.
3. Чем больше сторона треугольника, от которой исходит медиана, тем меньше эта медиана. И наоборот, самая короткая сторона имеет самую длинную медиану.
4. Медиана в прямоугольном треугольнике имеет ряд собственных характеристик. Например, если вокруг такого треугольника описать окружность, которая будет проходить через все вершины, то медиана прямого угла, проведенная к гипотенузе, станет радиусом описанной окружности (то есть ее длина будет составлять расстояние от любой точки окружности до ее центра).

Уравнение длины медианы треугольника

Формула медианы исходит из теоремы Стюарта и гласит, что медиана – это квадратный корень из отношения квадратов суммы сторон треугольника, которые образуют вершину, за вычетом квадрата стороны, к которой проведена медиана к четырем. Другими словами, чтобы узнать длину медианы нужно возвести в квадрат показатели длины каждой стороны треугольника, а затем записать это в виде дроби, в числителе которой будет сумма квадратов сторон, которые образуют угол, откуда исходит медиана, минус квадрат третьей стороны. В качестве знаменателя здесь выступает цифра 4. Затем из данной дроби нужно извлечь корень квадратный, и тогда мы получим длину медианы.

Точка пересечения медиан треугольника

Как мы писали выше, всем медианы одного треугольника пересекаются в одной точке. Эту точку называют центром треугольника. Он делит каждую медиану на две части, длина которым соотносится как 2:1. При этом центр треугольника является и центром описанной вокруг него окружности. А другие геометрические фигуры имеют собственные центры.

Координаты точки пересечения медиан треугольника

Чтобы найти координаты пересечения медиан одного треугольника, воспользуемся свойством центроида, согласно которому он делит каждую медиану на отрезки 2:1. Обозначаем вершины как как A(x 1 ;y 1), B(x 2 ;y 2), C(x 3 ;y 3),

и вычисляем координаты центра треугольника по формуле: x 0 = (x 1 + x 2 + x 3)/3; y 0 = (y 1 + y 2 + y 3)/3.

Площадь треугольника через медиану

Все медианы одного треугольника делят этот треугольник на 6 равных треугольников, а центр треугольника делит каждую медиану в соотношении 2:1. Поэтому если известны параметры каждой медианы, можно вычислить и площадь треугольника через площадь одного из маленьких треугольников, а затем увеличить этот показатель в 6 раз.

Медианой именуется отрезок, проведенный из вершины треугольника на середину противоположной стороны, то есть делит ее точкой пересечения пополам. Точка, в которой медиана пересекает противоположную вершине, из которой она выходит, сторону, именуется основанием. Через одну точку, называемую точкой пересечения, проходит каждая медиана треугольника. Формула длины ее может выражаться несколькими способами.

Формулы для выражения длины медианы

• Зачастую в задачах по геометрии ученикам приходится иметь дело с таким отрезком, как медиана треугольника. Формула ее длины выражается через стороны:

где a, b и c — стороны. Причем с является стороной, на которую медиана опускается. Таким образом выглядит самая простая формула. Медианы треугольника иногда требуется проводить для вспомогательных расчетов. Есть и другие формулы.

• Если при расчете известны две стороны треугольника и определенный угол α, находящийся между ними, то длина медианы треугольника, опущенной к третьей стороне, будет выражаться так.

Основные свойства

• Все медианы имеют одну общую точку пересечения O и ею же делятся в отношении два к одному, если вести отсчет от вершины. Такая точка носит название центра тяжести треугольника.
• Медиана разделяет треугольник на два других, площади которых равны. Такие треугольники называются равновеликими.
• Если провести все медианы, то треугольник будет разделен на 6 равновеликих фигур, которые также будут треугольниками.
• Если в треугольнике все три стороны равны, то в нем каждая из медиан будет также высотой и биссектрисой, то есть перпендикулярна той стороне, к которой она проведена, и делит надвое угол, из которого она выходит.
• В равнобедренном треугольнике медиана, опущенная из вершины, которая находится напротив стороны, не равной никакой другой, будет также высотой и биссектрисой.
  Медианы, опущенные из других вершин, равны. Это также является необходимым и достаточным условием равнобедренности.
• Если треугольник является основанием правильной пирамиды, то высота, опущенная на данное основание, проецируется в точку пересечения всех медиан.

• В прямоугольном треугольнике медиана, проведенная к наибольшей стороне, равняется половине ее длины.
• Пусть O — точка пересечения медиан треугольника. Формула, приведенная ниже, будет верная для любой точки M.

• Еще одним свойством обладает медиана треугольника. Формула квадрата ее длины через квадраты сторон представлена ниже.

Свойства сторон, к которым проведена медиана

• Если соединить любые две точки пересечения медиан со сторонами, на которые они опущены, то полученный отрезок будет являться средней линией треугольника и составлять одну вторую от стороны треугольника, с которой она не имеет общих точек.
• Основания высот и медиан в треугольнике, а также середины отрезков, соединяющих вершины треугольника с точкой пересечения высот, лежат на одной окружности.

В заключение логично сказать, что одним из самых важных отрезков является именно медиана треугольника. Формула ее может использоваться при нахождении длин других его сторон.

Медиана треугольника
— это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.

Свойства медиан треугольника

1. Медиана разбивает треугольник на два треугольника одинаковой площади.

2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника (центроидом).

3. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Длина медианы проведенной к стороне:
(док-во достроением до параллелограмма и использованием равенства в параллелограмме удвоенной суммы квадратов сторон и суммы квадратов диагоналей )

Т1.
Три медианы треугольника пересекаются в одной точке М, которая делит каждую из них в отношении 2:1, считая от вершин треугольника. Дано: ∆ABC,
СС 1 , АА 1 , ВВ
1 — медианы
∆ABC
. Доказать: и

Д-во: Пусть М — точка пересечения медиан СС 1 , АА 1 треугольника ABC. Отметим A 2 — середину отрезка AM и С 2 — середину отрезка СМ. Тогда A 2 C 2 — средняя линия треугольника АМС.
Значит,А 2 С 2
|| АС

и A 2 C 2 = 0,5*АС. С 1
А 1
— средняя линия треугольника ABC. Значит, А 1
С 1
|| АС и А 1
С 1
= 0,5*АС.

Четырехугольник А 2 С 1 А 1 С 2
— параллелограмм, так как его противо­положные стороны А

1
С 1
и А 2 С 2
равны и параллельны. Следовательно, А 2 М =
МА 1
и С 2 М =
МC 1 .
Это означает, что точки А 2
и M
делят медиану АА 2
на три равные части, т. е. AM = 2МА 2 . Аналогично СМ = 2MC 1
. Итак, точка М пересечения двух медиан АА 2
и CC 2
треугольника ABC делит каждую из них в отношении 2:1, считая от вершин треу­гольника. Совершенно аналогично доказывается, что точка пересечения меди­ан АА 1 и BB 1 делит каждую из них в отношении 2:1, считая от вер­шин треугольника.

На медиане АА 1 такой точкой является точка М, следовательно, точка М
и есть точка пересечения медиан АА 1 иBB 1.

Таким образом, n

T2.
Докажите, что отрезки, которые соединяют центроид с вер­шинами треугольника, делят его на три равновеликие части. Дано: ∆ABC , — его медианы.

Доказать:S AMB
=S BMC
=S AMC .
Доказательство.
В,
у них общая. т.к. равны их основания и высота, проведенная из вершины М,
у них общая. Тогда

Аналогичным образом доказывается, чтоS AMB = S AMC .
Таким образом,S AMB = S AMC = S CMB .
n

Биссектриса треугольника.Теоремы связанные с биссектрисами треугольника. Формулы для нахождения биссектрис

Биссектриса угла
— луч с началом в вершине угла, делящий угол на два равных угла.

Биссектриса угла есть геометрическое место точек внутри угла, равноудалённых от сторон угла.

Свойства

1. Теорема о биссектрисе: Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон

2. Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.

3. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса).

Вычисление длины биссектрисы

l c — длина биссектрисы, проведённой к стороне c,

a,b,c — стороны треугольника против вершин A,B,C соответственно,

p — полупериметр треугольника,

a l ,b l — длины отрезков, на которые биссектриса l c делит сторону c,

α,β,γ — внутренние углы треугольника при вершинах A,B,C соответственно,

h c — высота треугольника, опущенная на сторону c.

Метод площадей.

Характеристика метода.
Из названия следует, что главным объектом данного метода является площадь.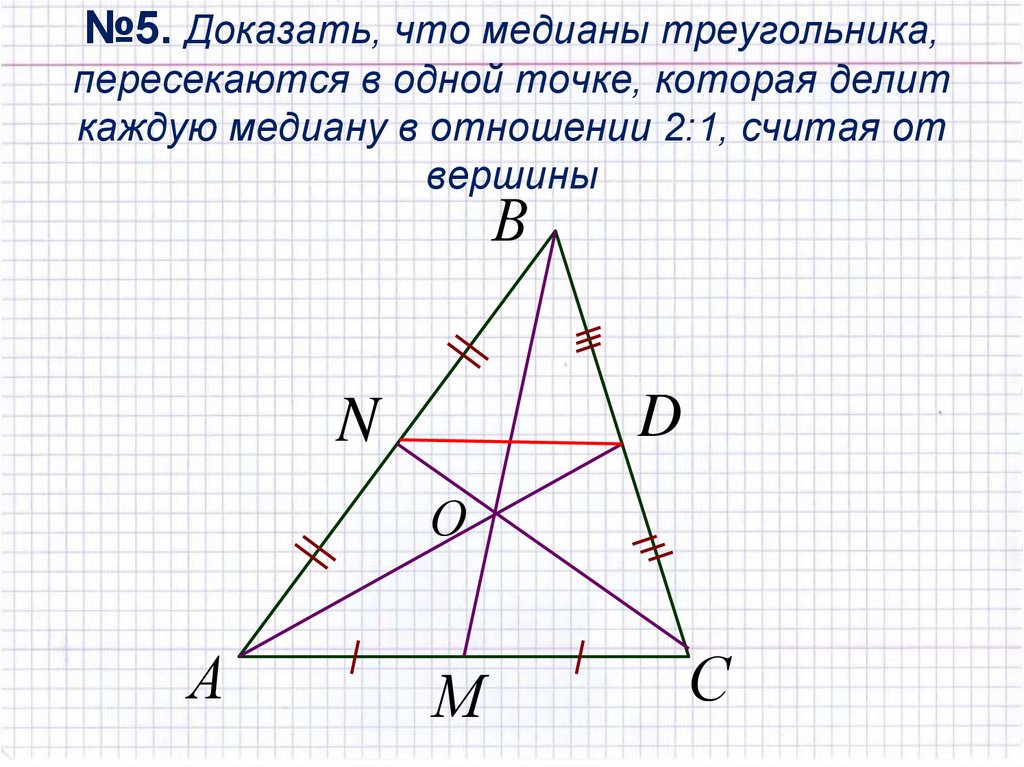 Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры (треугольника). Поэтому весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное. Здесь и проявляется основная особенность метода площадей – из геометрической задачи он «делает» алгебраическую, сводя все к решению уравнения (а иногда системы уравнений).

1) Метод сравнения: связан с большим кол-вом формул S одних и тех же фигур

2) Метод отношения S: основан на след опорных задачах:

Теорема Чевы

Пусть точки A»,B»,C» лежат на прямых BC,CA,AB треугольника. Прямые AA»,BB»,CC» пересекаются в одной точке тогда и только тогда, когда

Доказательство.

Обозначим через точку пересечения отрезков и . Опустим из точек С и А перпендикуляры на прямую ВВ 1 до пересечения с ней в точках Kи L соответственно (см.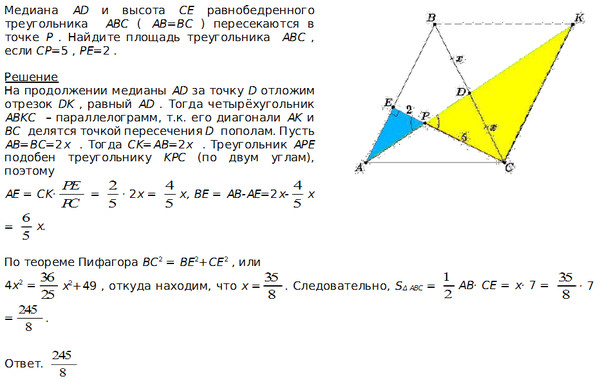 рисунок).

Поскольку треугольники и имеют общую сторону , то их площади относятся как высоты, проведенные на эту сторону, т.е. AL иCK:

Последнее равенство справедливо, так как прямоугольные треугольники и подобны по острому углу.

Аналогично получаем и

Перемножим эти три равенства:

что и требовалось доказать.

Замечание. Отрезок (или продолжение отрезка), соединяющий вершину треугольника с точкой, лежащей на противоположной стороне или ее продолжении, называется чевианой.

Теорема (обратная теорема Чевы)
. Пусть точки A»,B»,C» лежат на сторонах BC,CA и AB треугольника ABC соответственно. Пусть выполняется соотношение

Тогда отрезки AA»,BB»,CC» и пересекаются в одной точке.

Теорема Менелая

Теорема Менелая. Пусть прямая пересекает треугольник ABC, причем C 1 – точка ее пересечения со стороной AB, A 1 – точка ее пересечения со стороной BC, и B 1 – точка ее пересечения с продолжением стороны AC. Тогда

Доказательство

. Проведем через точку C прямую, параллельную AB. Обозначим через K ее точку пересечения с прямой B 1 C 1 .

ТреугольникиAC 1 B 1 иCKB 1 подобны (∟C 1 AB 1 = ∟KCB 1 , ∟AC 1 B 1 = ∟CKB 1). Следовательно,

ТреугольникиBC 1 A 1 иCKA 1 такжеподобны (∟BA 1 C 1 =∟KA 1 C, ∟BC 1 A 1 =∟CKA 1). Значит,

Из каждого равенства выразим CK:

Откуда что и требовалось доказать.

Теорема (обратная теорема Менелая).
Пусть дан треугольник ABC. Пусть точка C 1 лежит на стороне AB, точка A 1 – на стороне BC, а точка B 1 – на продолжении стороны AC, причем выполняется соотношение

Тогда точки A 1 ,B 1 и C 1 лежат на одной прямой.

Высоты Медианы и биссектрисы углов

Точно так же, как существуют специальные имена для особых типов треугольников, существуют специальные имена для особых отрезков внутри треугольников. Разве это не особенное?

База и высота

Каждый треугольник имеет три оснований (любая из его сторон) и три высот (высот). Каждая высота представляет собой перпендикулярный отрезок от вершины к противоположной стороне (или продолжение противоположной стороны) (рис. 1).

Рисунок 1  Три основания и три высоты одного и того же треугольника.

Высоты иногда могут совпадать со стороной треугольника или иногда могут пересекаться с расширенным основанием за пределами треугольника. На рисунке 2 AC — это высота основания BC , а BC — высота основания AC .

Рисунок 2  В прямоугольном треугольнике каждый катет может служить высотой.

На рис. 3, AM — высота до базы BC .

Рисунок 3  Высота тупоугольного треугольника.

Интересно отметить, что в любом треугольнике три прямые, содержащие высоты, пересекаются в одной точке (рис. 4).

Рисунок 4  Три линии, содержащие высоты, пересекаются в одной точке, 

, который может быть или не быть внутри треугольника.

Медиана

А медиана в треугольнике — это отрезок, проведенный от вершины к середине противоположной стороны. Каждый треугольник имеет три медианы. На рисунке 5 E является средней точкой BC . Следовательно, БЭ = ЭК . AE является медианой Δ ABC.

Рисунок 5  Медиана треугольника.

В каждом треугольнике три медианы сходятся в одной точке внутри треугольника (рис. 6).

Рисунок 6  Три медианы сходятся в одной точке внутри треугольника.

Биссектриса угла

Биссектриса угла в треугольнике — это отрезок, проведенный из вершины, которая делит пополам (разрезает пополам) этот угол при вершине. У каждого треугольника есть три биссектрисы угла. На рисунке , представляет собой биссектрису угла в Δ ABC.

Рисунок 7  Биссектриса угла.

В каждом треугольнике три биссектрисы угла пересекаются в одной точке внутри треугольника (рис. 8).

Рисунок 8  Биссектрисы трех углов пересекаются в одной точке внутри треугольника.

Как правило, высоты, медианы и биссектрисы являются разными отрезками. Однако в некоторых треугольниках они могут быть одними и теми же сегментами. На рисунке можно доказать, что высота, проведенная из угла при вершине равнобедренного треугольника, является медианой, а также биссектрисой угла.

Рисунок 9  Высота, проведенная из угла при вершине равнобедренного треугольника.

Пример 1: На основании маркировки на рисунке 10 назовите высоту Δ QRS, назовите медиану Δ QRS, и назовите биссектрису угла Δ QRS .

Рисунок 10  Нахождение высоты, медианы и биссектрисы угла.

RT является высотой до основания QS , потому что RT ⊥ QS .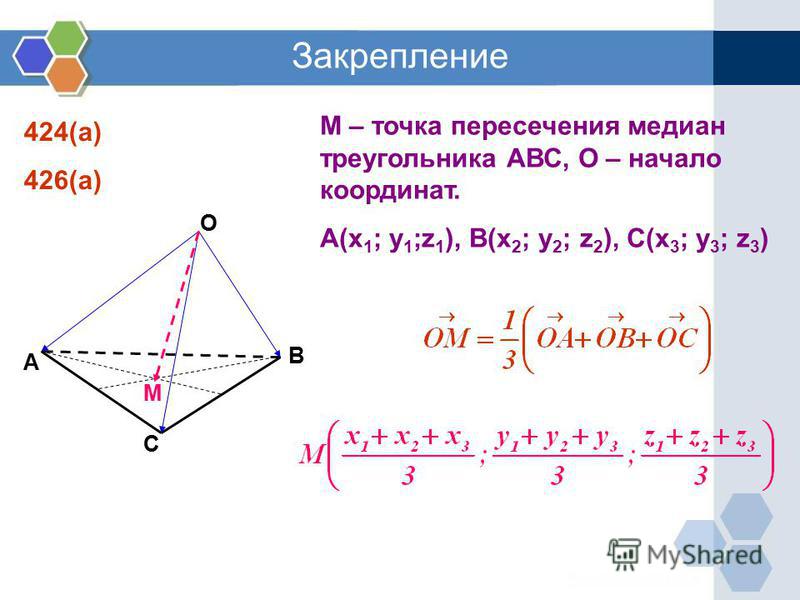

SP является медианой базы QR , поскольку P является средней точкой QR .

QU является биссектрисой угла Δ QRS , поскольку делит пополам ∠ RQS.

Калькулятор формул для уравнений равнобедренного треугольника

Изменить уравнение
Выберите, чтобы найти другое неизвестное

Разносторонний треугольник:
Стороны не имеют одинаковой длины
Нет равных углов

Уравнения разностороннего треугольника
Эти уравнения применимы к любому типу треугольника. Сокращенные
уравнений для равностороннего, прямого и равнобедренного треугольников приведены ниже.

	Perimeter
	Semiperimeter
	Area
	Area
	Base
	Height
	Angle Bisector стороны a
	Биссектриса угла стороны b
	Биссектриса угла стороны c
	Median of side a
	Median of side b
	Median of side c
	Altitude of side a
	Altitude of side b
	Высота стороны c
	Радиус описанной окружности
	Радиусы вписанной окружности

9 20003 .

	Длина стороны A
	Периметр
	Полупериметр
	Площадь
Высота 6
	Median
	Angle Bisector
	Circumscribed Circle Radius
	Inscribed Circle Radius

---

Right Triangle:
One angle is equal to 90 degrees

Уравнения прямоугольного треугольника

	Теорема Пифагора
	Периметр
	Semiperimeter
	Area
	Altitude of a
	Altitude of b
	Altitude of c
	Angle Bisector of a
	Биссектриса угла b
	Биссектриса угла c
	Медиана

Median of b
	Median of c
	Inscribed Circle Radius
	Circumscribed Circle Radius

7

---

Isosceles Triangle:
Two sides have equal length
Two angles are равно

Уравнения равнобедренного треугольника

	Периметр
	Полупериметр
	Area
	Altitudes of sides a and c
	Altitude of side b
	Median of sides a and c
	Median of side b
	Биссектриса угла сторон a и c
	Биссектриса угла стороны b
	Радиус описанной окружности	9167	0169	Inscribed Circle Radius

Where

= = .

P	=	Perimeter
s	=	Semiperimeter
a	=	Length of side a
b	=	Длина стороны b
c	=	Длина стороны c
h	9016 Высота над уровнем моря0172
m	=	Median
A	=	Angle A
B	=	Angle B
C	=	Angle C
T	=	Угол бисектор
R	=	RIGHTRED RADIUS
R
R
R
R
R	=
R	=
r	=
r	=

Найти медиану треугольника по координатам вершин

Как найти медиану если даны координаты вершин треугольника?

Чтобы найти медиану треугольника по координатам его вершин, применим формулы координат середины отрезка и формулу расстояния между точками.

Рассмотрим нахождение медианы на конкретном примере.

Дано: ΔABC,

1) Так как AF — медиана треугольника ABC, то F — середина BC.

Задачник «Векторный метод решения задач»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Задачник «Векторный метод решения задач»

Составила: Казакова Ольга Сергеевна,

учитель математики МОУ «СОШ № 75» г. Саратова.

Данный задачник предназначен для изучения тем: «Векторы», «Действия с векторами», «Векторный метод решения задач». Инструктивное изложение материала, при постоянной практической пробе, даёт возможность изучить темы самостоятельно.

№ 1.Заполните таблицу. Основные понятия.

Решение и изображение

1)На плоскости отметьте точки A и B , постройте отрезок AB ;

2)На отрезке AB пусть точка A будет началом, а точка B – концом. Укажите стрелкой в конце отрезка направление из начала в конец. Вы получили отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, то есть получили направленный отрезок или вектор .

3)Построен вектор , его можно обозначить и однострочной латинской буквой, например, , которая записывается над изображением вектора.

Сколько векторов можно провести, выбирая начало и конец среди данных на плоскости:

2)трёх точек, не лежащих на одной прямой;

3)четырёх точек, не лежащих на одной прямой?

Отметьте на плоскости любую точку и обозначьте её, например, заглавной буквой M . Вы построили нулевой вектор, его начало и конец совпадают.

Обозначение нулевого вектора: или символом .

1)Постройте отрезок AB , длина которого 4 см;

2)Постройте вектор .

Длиной или модулем ненулевого вектора называется длина отрезка AB .

Обозначение: = AB = 4.

Чему равна длина нулевого вектора?

3)Постройте вектор , длиной 7 см.

1)Постройте параллельные прямые p и m .

2)На прямой p постройте:

а)вектор , произвольной длины и направления;

б)вектор , произвольной длины и направления;

3)На прямой m постройте: вектор , произвольной длины и направления.

Ненулевые векторы называются коллинеарными , если они лежат либо на одной прямой, либо на параллельных прямых.

Нулевой вектор считается коллинеарным любому вектору.

4)Выпишите попарно коллинеарные векторы.

5)Постройте и обозначьте два произвольных вектора, которые являются не коллинеарными вектору . Будут ли они являться коллинеарными векторам , ?

Постройте два коллинеарных вектора.

Полученные векторы направлены одинаково или противоположно?

Если одинаково, то вы построили сонаправленные векторы. Обозначение:

 .

Если противоположно, то вы построили противоположно направленные векторы. Обозначение:  .

Начертите параллелограмм ABCD . Проведите векторы, начало и конец которых совпадают с какими-то двумя вершинами параллелограмма. Сколько существует пар векторов, которые являются:

1)коллинеарными друг другу;

Постройте векторы и , так, чтобы:

1)  ;

2) .

Вы построили равные векторы.

Векторы называются равными , если они сонаправлены и их длины равны.

№ 2.Заполните таблицу. Операции над векторами.

Решение и изображение

На плоскости произвольно выберите точку A , приняв её за начало, проведите вектор , произвольной длины и направления. Таким образом, вы отложили вектор от точки A .

Можно отложить от другой точки плоскости, вектор, равный данному вектору ?

Допустим, что вектор ненулевой, а точки A и B – его начало и конец.

1)Через произвольно взятую точку M плоскости проведите прямую p , параллельную AB (если M – точка прямой AB , то в качестве прямой p возьмём саму прямую AB ).

2)На прямой p отложите два противоположно направленных вектора и , длины которых равны отрезку AB .

Среди построенных векторов выберите тот, что сонаправлен с вектором , он и будет являться искомым вектором, равным вектору . К тому же такой вектор только один, что следует из построения.

А если вектор – нулевой? Ответьте самостоятельно.

Итак, от любой точки M можно отложить вектор, равный данному вектору , и при том только один.

1)Векторы и .

2)Произвольная точка A .

3)От точки A отложите вектор , равный вектору .

4)От точки B отложите вектор , равный вектору .

5)Вектор .

Вы, таким образом, выполнили построение сложения векторов и по правилу треугольника . Вектор называется суммой векторов и .

Докажем, что если и , то .

Рассмотрим случай, когда точки A , B , , точки B , C , и точки A , C , не лежат на одной прямой (остальные случаи рассмотрите самостоятельно).

а) ;

б) ;

в)Соединим точки A и , B и , C и ;

2)  – параллелограмм  ;

3)  – параллелограмм  ;

4)Из 2) и 3)   – параллелограмм;

5)Значит, . Доказано.

Вывод: при необходимости можно работать как с данными векторами, так и с равными им.

Законы сложения векторов.

Для любых векторов , и справедливы равенства:

(переместительный закон)

(сочетательный закон)

Доказательство законов проведите самостоятельно, опираясь на подсказки:

Для доказательства первого закона можете достроить треугольник до параллелограмма и работать как с самими векторами, так и с равными им.

Для доказательства второго закона достаточно несколько раз применить правило треугольника для сложения векторов, последовательно отложенных от концов предыдущих векторов.

1)Произвольная точка A ;

2)Неколлинеарные векторы и ;

3) От точки A отложите вектор , равный вектору .

4)От точки A отложите вектор , равный вектору .

5)Постройте параллелограмм ABCD ;

6) .

Вы построили сложение векторов и по правилу параллелограмма сложения неколлинеарных векторов.

Как сложить несколько векторов?

Последовательное применение правила треугольника для сложения векторов даёт возможность сложить любое количество векторов. Причём порядок сложения не важен. Сложение нескольких векторов производится следующим образом: два вектора складываются, получившаяся сумма складывается с третьим и т.д.

Выполните сложение пяти любых векторов, используя то, что несколько векторов можно расположить таким образом: первый вектор откладывается от любой точки, второй – от конца первого и т.д. Сумма всех векторов – вектор, направленный от начала первого вектора к концу последнего.

Вы выполнили построение сложения нескольких векторов, пользуясь правилом многоугольника .

Подумайте, чему будет равна сумма векторов, если начало первого вектора совпадает с концом последнего?

Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору .

Вектор называется противоположным вектору , если векторы и имеют равные длины и противоположно направлены. Обозначение: . .

Докажите, что . Для этого воспользуйтесь определением разности векторов и прибавлением к обеим частям равенства вектора.

На прямой p от любой точки O отложите вектор , от конца вектора отложите вектор . Длина построенного суммарного вектора, равна или .

Произведением ненулевого вектора на число k называется такой вектор , длина которого равна , причём векторы и сонаправлены при k  0 и противоположно направлены при k .

Произведением нулевого вектора на любое число считается нулевой вектор.

Из определения следует:

1)произведение любого вектора на число нуль есть нулевой вектор;

2)для любого числа k и любого вектора векторы и коллинеарны.

Свойства умножения вектора на число.

Для любых чисел k , l и любых векторов , справедливы равенства:

(сочетательный закон)

(первый распределительный закон)

(второй распределительный закон)

На прямой p от произвольно выбранной точки O отложите: вектор , длиной 1 см; вектор , сонаправленный с вектором , длиной 2 см; вектор , противоположно направленный с вектором , длиной 3 см.

Попробуем выразить векторы и через вектор .

Во сколько раз длины этих векторов отличаются от длины вектора ?

; ;

 ,  , т. е. векторы , и коллинеарны друг другу, значит, можно воспользоваться леммой.

Если векторы и коллинеарны и , то существует такое число k , что .

Итак, можем выразить: , .

От произвольной точки O отложите векторы и , и – произвольные данные векторы. Если и не являются сонаправленными, то лучи OA и OB образуют угол AOB , градусную меру которого обозначьте буквой α. Будем говорить, что угол между векторами и равен α. Обозначение: .

Если  , то

Если , то векторы и называются перпендикулярными.

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

Напишите формулу скалярного произведения для случаев, когда:

;

;

.

Сделайте вывод, о том, в каком случае скалярное произведение двух векторов равно нулю.

Напишите формулу скалярного произведения для случая, когда вектор скалярно умножается на себя. В этом случае скалярное произведение называется скалярным квадратом . Обозначение: .

Итак, перечислите все операции над векторами.

№ 3.Решая задачи, заполните пустые ячейки в таблице.

k , что ,

точки M и N совпадают

точка C принадлежит прямой AB

, или
, или

точка С – середина отрезка AB

точка D разбивает отрезок AC так, что AD : DC = m : n

Заполняя таблицу, вы пользовались векторным методом решения задач.

Векторный метод – один из наиболее общих методов решения геометрических задач.

Для решения задач элементарной геометрии с помощью векторов необходимо, прежде всего, научиться «переводить» условие геометрической задачи на «векторный» язык. После такого перевода осуществляются алгебраические вычисления с векторами, а затем полученное снова «переводится» на «геометрический» язык. В этом и состоит сущность векторного метода решения геометрических задач.

Далее вам необходимо самостоятельно решать задачи. После решения каждой задачи делайте вывод о её значимости. Если результат задачи возможно использовать для решения других, то заносите его в таблицу № 3. Таким образом, вы получите набор базовых задач, на основании которых решаются более сложные.

1)Докажите, что средняя линия треугольника параллельна его третьей стороне и равна её половине.

2)Докажите, что средняя линия трапеции параллельна её основанию и её длина равна полусумме длин её оснований.

3)Если средняя линия четырёхугольника равна полусумме длин её оснований (сторон, не имеющих общей точки со средней линией), то этот четырёхугольник является трапецией или параллелограммом.

4)Около окружности описана равнобочная трапеция ABCD . Точки E и K – точки касания этой окружности с боковыми сторонами AB и CD . Докажите, что отрезок EK параллелен основаниям трапеции.

5)Докажите, что биссектриса угла треугольника делит его сторону на отрезки, пропорциональные прилежащим сторонам. Выразите биссектрису через угол треугольника, который она делит пополам, и через стороны этого угла.

6)Если точки M и N делят отрезки AB и CD соответственно в равных отношениях так, что AM : MB = CN : ND = m : n , то выполняется равенство: .

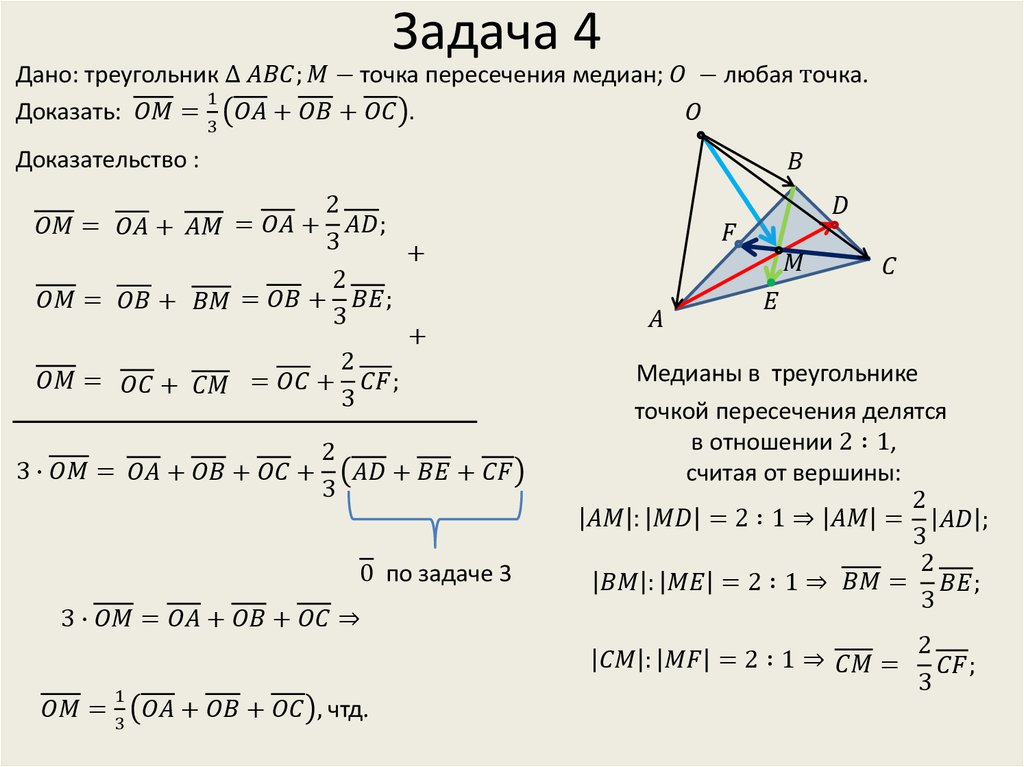
7)В треугольнике ABC через M обозначена точка пересечения медиан. Докажите, что .

8)Пусть M – точка пересечения медиан треугольника ABC , O – произвольная точка. Докажите, что .

9)Пусть H – точка пересечения высот треугольника ABC , O – центр описанной окружности. Докажите, что .

10)Докажите, что три точки A , B , C ( A ≠ B ) лежат на одной прямой тогда и только тогда, когда имеет место равенство, , в котором α+β=1, где O – некоторая точка.

11)Докажите, что центр описанной окружности

12)Докажите, что если точки пересечения диагоналей четырёхугольника и середины двух его противоположных сторон лежат на одной прямой, то этот четырёхугольник – трапеция или параллелограмм.

13)Докажите, что медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.

14)Докажите, что биссектрисы треугольника пересекаются в одной точке.

15)Докажите, что высоты треугольника пересекаются в одной точке.

16)Докажите, что четырёхугольник является параллелограммом тогда и только тогда, когда его диагонали в точке пересечения делятся пополам.

17)Докажите, что в произвольном четырёхугольнике средние линии (т. е. отрезки, соединяющие середины противоположных сторон) точкой их пересечения делятся пополам.

18)Найти косинус угла между диагоналями прямоугольника, стороны которого равны a и b .

19)Докажите, что диагонали ромба взаимно перпендикулярны.

20)Докажите, что вписанный угол, опирающийся на диаметр окружности, — прямой.

21)Докажите, что если в треугольнике длины его сторон a , b , c связаны соотношением , то угол этого треугольника, лежащий против стороны длины c , — прямой.

22)Даны стороны a , b , c треугольника. Найдите медианы , , , проведённые к этим сторонам.

23)В треугольнике со сторонами a , b , c найти длину высоты , опущенную на сторону c .

24)В треугольнике со сторонами a , b , c найти длину биссектрисы , проведённой к стороне c .

25)Докажите, что сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин всех его сторон.

26)Докажите, что сумма квадратов длин диагоналей трапеции равна сумме квадратов длин её боковых сторон плюс удвоенное произведение длин оснований.

27)Доказать, что большей медиане треугольника соответствует меньшая сторона и обратно.

28)Докажите, диагонали прямоугольника равны между собой.

29)Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям и равен их полуразности.

30)В четырёхугольнике ABCD прямая, проведённая через вершину A параллельна стороне BC , пересекает диагональ BD в точке M , а прямая проведённая через вершину B параллельно стороне AD , пересекает диагональ AC в точке N . Докажите, что MN || DC .

31)Четыре окружности радиуса R пересекаются по три в точках M и N , и по две в точках A , B , C , D . Докажите, что ABCD – параллелограмм.

32)Пусть K , L , M , N – середины отрезков AB , BC , CD , DE пятиугольника ABCDE , а точки P и Q – середины отрезков KM и LN соответственно. Докажите, что отрезок PQ в четыре раза меньше стороны AE и параллелен ей.

33)В плоскости даны четырёхугольник ABCD и точка M . Докажите, что точки, симметричные точке M относительно середин сторон этого четырёхугольника, являются вершинами параллелограмма.

34)На диагоналях AC и CE правильного шестиугольника ABCDEF взяты точки M и N соответственно, такие, что AM : AC = CN : CE = λ. Известно, что точки B , M , N лежат на одной прямой. Найдите λ.

35)Дан параллелограмм ABCD ( AD || BC , AB || CD ). На стороне AD выбрана точка K , а на AC – точка L так, что 5 AK = AD , 6 AL = AC . Докажите, что KL || BL и найдите отношение их длин.

36)Точки M и K на сторонах AB и BC треугольника ABC таковы, что AM : MB =3:4, CK : KB =2:3. Отрезки AK и CM пересекаются в точке N . Найдите отношение AN : NK .

37)Точка K на стороне AC и точки L , M на стороне BC треугольника ABC таковы, что AK : KC = CL : LB = BM : MC =1:2, N – середина стороны AC . Найти отношение, в котором точка пересечения отрезков KL и MN делит отрезок KL .

38)Через середину E медианы треугольника ABC проведена прямая AE , пересекающая сторону BC в точке F . Вычислить: AE : EF и CF : FB .

39)Дан параллелограмм ABCD . Точка M делит сторону AD в отношении p , т. е. AM : MD = p ; точка N делит сторону DC в отношении q , т. е. DN : NC = q . Прямые BM и AN пересекаются в точке S . Вычислить отношения AS : SN и BS : SM .

40)В параллелограмме ABCD сторона AD разделена на n равных частей и первая точка деления M (считая от A ) соединена с B . В каком отношении делит точка N диагональ AC и отрезок MB ?

41)В треугольнике ABC проведена медиана CM . Прямая l пересекает отрезки CA , CM , CB в точках , , соответственно. Докажите равенство .

42)На сторонах AC и BC треугольника ABC взяты точки M и D так, что AM = AC , BD = BC , а на прямой AD – точка N так, что AN = AD . Доказать, что точки M , N и B лежат на одной прямой. Какую часть от отрезка MB составляет отрезок MN ?

43)На стороне AD и диагонали AC параллелограмма ABCD взяты точки M и N так, что AM = AD , AN = AC . Доказать, что точки M , N и B лежат на одной прямой. В каком отношении делит точка N отрезок MB ?

44)На стороне AB треугольника ABC дана точка P , через которую проведены прямые параллельно его медианам A и A и пересекающие соответственно стороны треугольника в точках и . Докажите, что середина отрезка (точка E ), а также точка P и точка G пересечения медиан треугольника лежат на одной прямой и найдите отношение длин отрезков EG и EP .

45)Докажите, что точки пересечения диагоналей трапеции, боковых сторон, а также середины оснований лежат на одной прямой.

46)Через точку P – внутреннюю точку параллелограмма ABCD – проведены прямая KM || AD и прямая LN || AB , пересекающие стороны AB , BC , CD , DA параллелограмма в точках K , L , M , N соответственно. Q – точка пересечения средних линий четырёхугольника KLMN , S – точка пересечения диагоналей параллелограмма ABCD . Докажите, что Q – середина отрезка PS .

47)Пусть , , – середины сторон BC , AC , AB треугольника ABC . Доказать, что точки пересечения медиан треугольника ABC и треугольника совпадают.

48)Пусть ABCDEF – произвольный шестиугольник и U , V , W , X , Y , Z – середины его сторон. Докажите, что центры тяжести (т. е. точки пересечения медиан) треугольника UWY и треугольника VXZ совпадают.

49)Докажите, что прямая, соединяющая середины оснований трапеции, и продолжения боковых сторон трапеции пересекаются в одной точке.

50)На сторонах параллелограмма заданы точки, которые делят стороны в одном и том же отношении (в каком-либо одном направлении обхода). Докажите, что точки деления служат вершинами параллелограмма, а центры этих параллелограммов совпадают.

51)На сторонах треугольника заданы точки, которые делят стороны в одном и том же отношении (в каком-либо одном направлении обхода). Докажите, что точки пересечения медиан данного треугольника и треугольника, имеющего вершинами точки деления, совпадают.

52)В треугольнике ABC длины сторон связаны соотношением . Докажите, что медианы, проведённые к сторонам AC и BC , взаимно перпендикулярны.

53)Найдите косинус угла между медианами прямоугольного равнобедренного треугольника, проведёнными к его катетам.

54)Найти косинус угла между медианами равнобедренного треугольника, проведёнными к его боковым сторонам, при условии, что угол при вершине равен α.

55)Найти косинус угла при вершине равнобедренного треугольника, если медианы, проведённые к его боковым сторонам, а) перпендикулярны; б) образую угол .

56)В треугольнике две стороны равны 2 и 4, а угол между ними равен . Найти угол ψ между короткой стороной и медианой, проведённой к третьей стороне.

57)В окружности с центром O радиуса r вписан четырёхугольник ABCD . Доказать, что если , то диагонали четырёхугольника взаимно перпендикулярны.

58)В прямоугольнике ABCD опущен перпендикуляр BK на диагональ AC . Точки M и N – середины отрезков AK и CD соответственно. Докажите, что угол BMN прямой.

59)На стороне AB треугольника ABC с углом ABC , равным α , расположена точка K , причём AK = BC . Пусть P – середина BK , M – середина AC . Найдите угол APM .

60)Точка K – середина стороны AB квадрата ABCD , а точка M лежит на диагонали AC , причём AM : MC = 3 : 1. Докажите, что угол KMD равен .

61)На сторонах AB и AC треугольника ABC во внешнюю сторону построены квадраты AMNB и CKLA . Докажите, что медиана AP треугольника ABC перпендикулярна прямой ML .

62)На стороне AB треугольника ABC дана точка D . Выразить расстояние CD через длины сторон данного треугольника a , b , c и расстояния AD = m и DB = n .

63)Выразить расстояние от заданной точки O до точки M пересечения медиан треугольника ABC через длины сторон треугольника BC = a , AC = b , AB = c и расстояния от точки O до вершин треугольника OA = , OB = , OC = .

64)В параллелограмме ABCD точка K – середина стороны BC , а точка M – середина стороны CD . Найдите AD , если AK = 6, AM = 3,  KAM = .

Список использованной литературы

Атанасян Л.С. и др. Геометрия. Учебник для 7-9 кл. общеобразовательных учреждений. – М.: Просвещение, 2003.

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия. 10-11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни. – М.: Просвещение, 2009.

Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Шестаков С.А., Юдина И.И. Планиметрия. Пособие для углубленного изучения математики – М.: ФИЗМАТЛИТ, 2005.

Василевский А.Б. Методы решения геометрических задач. – Минск: Вышэйш. школа, 1965.

Габович И.Г. Алгоритмический подход к решению геометрических задач. – М.: Просвещение, 1996.

Гордин Р.К. Геометрия. Планиметрия 7-9 кл. – М.: МЦНМО, 2006.

Готман Э.Г., Скопец З.А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9 и 10 кл. – М.: Просвещение, 1979.

Гусев В. А. и др. Практикум по элементарной математике: Геометрия: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов и учителей. – М.: Просвещение, 1992.

Зеленяк О. П. Решение задач по планиметрии. Технология алгоритмического подхода на основе задач-теорем. Моделирование в среде Turbo Pascal. – Киев, Москва: ДиаСофтЮП, ДМК Пресс, 2008.

Шарыгин И. Ф. Геометрия. 7 – 9 кл.: Учеб. для общеобразоват. учеб. завед. – М.: Дрофа, 2001.

Шарыгин И.Ф. Решение задач: Учеб. пособие для 10 кл. общеобразоват. учреждений. – М.: Просвещение, 1994.

Шестаков С. А. Векторы на экзаменах. Векторный метод в стереометрии. – М.: МЦНМО, 2005.

Мой любимый алгоритм: нахождение медианы за линейное время

Нахождение медианы за O(n log n)

Самым прямолинейным способом нахождения медианы является сортировка списка и выбор медианы по её индексу. Самая быстрая сортировка сравнением выполняется за O(n log n) , поэтому от неё зависит время выполнения 1 , 2 .

У этого способа самый простой код, но он определённо не самый быстрый.

Нахождение медианы за среднее время O(n)

Следующим нашим шагом будет нахождение медианы в среднем за линейное время, если нам будет везти. Этот алгоритм, называемый «quickselect», разработан Тони Хоаром, который также изобрёл алгоритм сортировки с похожим названием — quicksort. Это рекурсивный алгоритм, и он может находить любой элемент (не только медиану).

1. Выберем индекс списка. Способ выбора не важен, на практике вполне подходит и случайный. Элемент с этим индексом называется опорным элементом (pivot).
2. Разделим список на две группы:
   1. Элементы меньше или равные pivot, lesser_els
   2. Элементы строго большие, чем pivot, great_els
3. Мы знаем, что одна из этих групп содержит медиану. Предположим, что мы ищем k-тый элемент:
   • Если в lesser_els есть k или больше элементов, рекурсивно обходим список lesser_els в поисках k-того элемента.
   • Если в lesser_els меньше, чем k элементтов, рекурсивно обходим список greater_els . Вместо поиска k мы ищем k-len(lesser_els) .

Вот пример алгоритма, выполняемого для 11 элементов:

Чтобы найти с помощью quickselect медиану, мы выделим quickselect в отдельную функцию. Наша функция quickselect_median будет вызывать quickselect с нужными индексами.

В реальном мире Quickselect отлично себя проявляет: он почти не потребляет лишних ресурсов и выполняется в среднем за O(n) . Давайте докажем это.

Доказательство среднего времени O(n)

В среднем pivot разбивает список на две приблизительно равных части. Поэтому каждая последующая рекурсия оперирует с 1 ⁄₂ данных предыдущего шага.

Существует множество способов доказательства того, что этот ряд сходится к 2n. Вместо того, чтобы приводить их здесь, я сошлюсь на замечательную статью в Википедии, посвящённую этому бесконечному ряду.

Quickselect даёт нам линейную скорость, но только в среднем случае. Что, если нас не устраивает среднее, и мы хотим гарантированного выполнения алгоритма за линейное время?

Детерминированное O(n)

В предыдущем разделе я описал quickselect, алгоритм со средней скоростью O(n) . «Среднее» в этом контексте означает, что в среднем алгоритм будет выполняться за O(n) . С технической точки зрения, нам может очень не повезти: на каждом шаге мы можем выбирать в качестве pivot наибольший элемент. На каждом этапе мы сможем избавляться от одного элемента из списка, и в результате получим скорость O(n^2) , а не O(n) .

С учётом этого, нам нужен алгоритм для подбора опорных элементов. Нашей целью будет выбор за линейное время pivot, который в худшем случае удаляет достаточное количество элементов для обеспечения скорости O(n) при использовании его вместе с quickselect. Этот алгоритм был разработан в 1973 году Блумом (Blum), Флойдом (Floyd), Праттом (Pratt), Ривестом (Rivest) и Тарьяном (Tarjan). Если моего объяснения вам не хватит, то можете изучить их статью 1973 года. Вместо того, чтобы описывать алгоритм, я подробно прокомментирую мою реализацию на Python:

Давайте докажем, что медиана медиан является хорошим pivot. Нам поможет, если мы представим визуализацию нашего алгоритма выбора опорных элементов:

Красным овалом обозначены медианы фрагментов, а центральным кругом — медиана медиан. Не забывайте, мы хотим, чтобы pivot разделял список как можно ровнее. В худшем возможном случае каждый элемент в синем прямоугольнике (слева вверху) будет меньше или равен pivot. Верхний правый прямоугольник содержит 3 ⁄₅ половины строк — 3/5*1/2=3/10 . Поэтому на каждом этапе мы избавляемся по крайней мере от 30% строк.

Но достаточно ли нам отбрасывать 30% элементов на каждом этапе? На каждом этапе наш алгоритм должен выполнять следующее:

• Выполнять работу O(n) по разбиению элементов
• Для рекурсии решать одну подзадачу размером в 7 ⁄₁₀ от исходной
• Для вычисления медианы медиан решать одну подзадачу размером с 1 ⁄₅ от исходной

В результате мы получаем следующее уравнение полного времени выполнения T(n) :

Не так уж просто доказать, почему это равно O(n) . Быстрое решение заключается в том, чтобы положиться на основную теорему о рекуррентных соотношениях. Мы попадаем в третий случай теоремы, при котором работа на каждом уровне доминирует над работой подзадач. В этом случае общая работа будет просто равна работе на каждом уровне, то есть O(n) .

Подводим итог

У нас есть quickselect, алгоритм, который находит медиану за линейное время при условии наличия достаточно хорошей опорного элемента. У нас есть алгоритм медианы медиан, алгоритм O(n) для выбора опорного элемента (который достаточно хорош для quickselect). Соединив их, мы получили алгоритм нахождения медианы (или n-ного элемента в списка) за линейное время!

Медианы за линейное время на практике

В реальном мире почти всегда достаточно случайного выбора медианы. Хотя подход с медианой медиан всё равно выполняется за линейное время, на практике его вычисление длится слишком долго. В стандартной библиотеке C++ используется алгоритм под названием introselect, в котором применено сочетание heapselect и quickselect; предел его выполнения O(n log n) . Introselect позволяет использовать обычно быстрый алгоритм с плохим верхним пределом в сочетании с алгоритмом, который медленнее на практике, но имеет хороший верхний предел. Реализации начинают с быстрого алгоритма, но возвращаются к более медленному, если не могут выбрать эффективные опорные элементы.

В завершение приведу сравнение элементов, используемых в каждой из реализаций. Это не скорость выполнения, а общее количество элементов, которые рассматривает функция quickselect. Здесь не учитывается работа по вычислению медианы медиан.

Именно этого мы и ожидали! Детерминированный опорный элемент почти всегда рассматривает при quickselect меньшее количество элементов, чем случайный. Иногда нам везёт и мы угадываем pivot с первой попытки, что проявляется как впадины на зелёной линии. Математика работает!

1. Это может стать интересным применением поразрядной сортировки (radix sort), если вам нужно найти медиану в списке целых чисел, каждое из которых меньше 2 32 .
2. На самом деле в Python используется Timsort, впечатляющее сочетание теоретических пределов и практической скорости. Заметки о списках в Python.

Медиана треугольника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны, а также прямая, содержащая этот отрезок.

Каждый треугольник имеет ровно три медианы, по одной из каждой вершины, и все они пересекаются друг с другом в центре треугольника. В случае равнобедренного и равностороннего треугольников, медиана делит пополам любой угол в вершине у которого две смежные стороны равны.

Калькулятор длины медианы треугольника

Онлайн калькулятор расчета длины медианы треугольника при условии, что известны координаты его вершин. Нахождение длины трех медиан треугольника

Формула расчета длины медианы

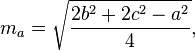
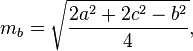
где,

• a,b,c — Длина сторон треугольника.

Пример расчета медиан:

Даны точки A( 1 , 5 ), B( 8 , 9 ) и C( 5 , 6 ). Найдите медианы треугольника.

Получаем:

A( 1 , 5 ) B( 8 , 9 ) C( 5 , 6 )

Решение:

Шаг 1:

Найдем длину сторон a,b,c используя формулу

d = √((x₂ — x₁)² + (y₂ — y₁)²⁾

Найдем длину стороны A между точками B( 8 , 9 ) and C( 5 , 6 )

a = √((5 — ² + (6 — 9)² )= 4.242

Найдем длину стороны B между точками C( 5 , 6 ) и A( 1 , 5 )

b = √((1 — 5)² + (5 — 6)²⁾ = 4.123

Найдем длину стороны C между точками A( 1 , 5 ) и B( 8 , 9 )

c = √((8 — 1)² + (9 — 5)²⁾ = 8.062

Шаг 2:

Полученные значения a,b,c применяем в формулы

m_a = (1/2) √2c² + 2b² — a²

m_b = (1/2) √(2c² + 2a² — b² )

m_c = (1/2) √(2a² + 2b² — c² )

• m_a = (1/2)√(2(8.062)² + 2(4.123)² — 4.242² )= 6.042
• m_b = (1/2)√(2(8.062)² + 2(4.242)² — 4.123² )= 6.103
• m_c = (1/2)√2(4.242)² + 2(4.123)² — 8.062² = 1.118

Свойства Медиан Треугольника

• Медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
• Треугольник делится тремя медианами на шесть равновеликих треугольников.
• Большей стороне треугольника соответствует меньшая медиана.
• В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равняется половине гипотенузы.
• Из отрезков, образующих медианы, можно составить треугольник, то есть их длины удовлетворяют неравенству треугольника.

людей нашли эту статью полезной. А Вы?

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.