Рассмотрим задачи, в которых требуется по рисунку на клетчатой бумаге найти длину медианы треугольника.
Задачи.
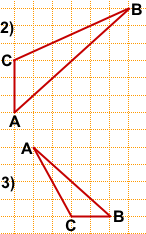
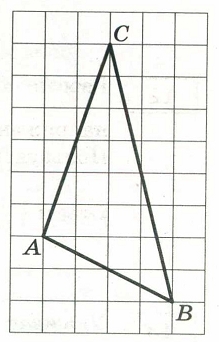
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его медианы, проведённой из вершины C.
Решение:
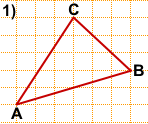
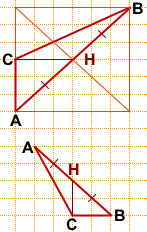
Следовательно, задачу начинаем с нахождения середины AB.
Как правило, сторона AB в таких задачах изображается не горизонтальным или вертикальным отрезком.
Длину медианы CH считаем по клеточкам — CH=4.
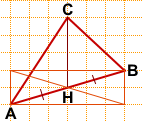
2) Аналогично предыдущей задаче, сначала найдём середину отрезка AB.
Можно достроить прямоугольник с диагональю AB, провести вторую диагональ и отметить точку H пересечения диагоналей.
Длину медианы CH находим по клеточкам:
CH=3.
3) Можно найти середину отрезка AB и без дополнительных построений.
Например, можно рассуждать так:
AH=BH как диагонали равных квадратов (со стороной 2 клетки), следовательно, точка H — середина AB, CH — медиана треугольника ABC.
CH=2.
Если медиана треугольника расположена не горизонтально либо вертикально, посчитать её длину по клеточкам не удастся.
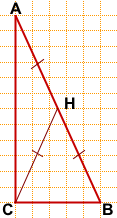
То есть для нахождения длины медианы нужно знать гипотенузу.
Длины катетов определяем по клеточкам: AC=12, BC=5.
По теореме Пифагора: AB²=AC²+BC²,
AB²=12²+5²=169, AB=13,
CH= 1/2 AB=6,5.
5) 
(достаточно провести вторую диагональ, прямоугольник можно не строить).
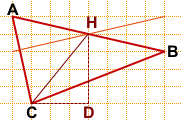
Достроим прямоугольный треугольник CHD с гипотенузой CH.
CD=3, HD=4.
CH находим по теореме Пифагора (можно также заметить, что CHD — египетский треугольник): CH=5.
Рубрика Задание 3, Решаем ЕГЭ по математике Комментарии (0)
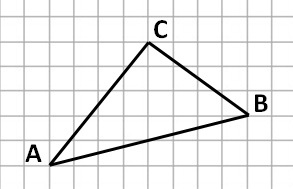
Задание. На клетчатой бумаге с размером клетки 1 × 1 изображен треугольник АВС. Найдите длину его медианы, проведенной из вершины С.
Решение:
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
Найдем середину стороны АВ и проведем отрезок СМ. Отрезок СМ – медиана треугольника АВС.
По клеточкам легко найти, что СМ = 4.
Ответ: 4
Понравилось? Нажмите
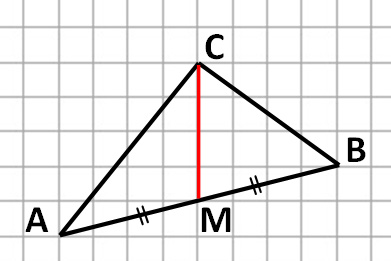
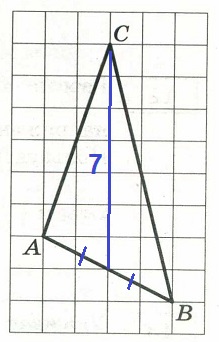
На клетчатой бумаге с размером клетки 1 x 1 изображён треугольник АВС. Найдите длину его медианы, проведённой из вершины С.
Источник задания: ОГЭ 2021 Математика, И.В. Ященко. 36 вариантов.
Решение:
Медиана из вершины С будет делить противолежащую сторону АВ на две равные части:
Длинна её равна 7 клеток.
Ответ: 7.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.6 / 5. Количество оценок: 16
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
На клетчатой бумаге с размером клетки $1$ см $×$ $1$ см изображён треугольник $ABC$ (см. рис. ). Найдите длину его медианы, проведённой из вершины $B$ (в сантиметрах).
Длина медианы проведённой из $B$, равна половине длины гипотенузы в $△ABC, ∠B = 90°. AC^2 = AB^2 + BC^2; AC^2 = 144 + 25 = 169, AC = 13. m_B = {AC}/{2}= {13}/{2}=6.5$.
Ответ: 6.5
Вы отправили работу на проверку эксперту. Укажите номер телефона на него придет СМС
Отправить
Незнайка → ЕГЭ → Математика → Профильная → Вариант 3 → Задание 3
Задание № 21781
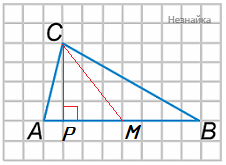
На клетчатой бумаге с размером клетки 1 см × 1 см изображён треугольник. Найдите длину медианы, проведенной из вершины C. Ответ дайте в см.
Показать ответ
Комментарий:
CM — медиана, CP — высота. В прямоугольном треугольнике CMP: CP=4, PM=3. По теореме Пифагора находим CM=√(CP2+PM2)=√(42+32)=5
Ответ: 5
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.
2 306 766
Уже готовятся к ЕГЭ, ОГЭ и ВПР.
Присоединяйся!
Мы ничего не публикуем от вашего имени