Как найти медиану векторного треугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Найти медиану треугольника по координатам вершин

Вектор и треугольник и медиана

Медиана треугольника

Свойство вектора медианы треугольника

Медиана треугольника

Медиана угла

Определение и свойства медианы треугольника

Определение медианы треугольника

Свойства медианы

Примеры задач

Применение векторов к решению задач

Применение векторов к решению задач

Найти медиану треугольника по координатам вершин

Свойство 1 (основное)

Свойство 2

Свойство 3

Свойство 4

Свойство 5

Этот видеоурок доступен по абонементу

Этот видеоурок доступен по абонементу

Как найти медиану если даны координаты вершин треугольника?

Чтобы найти медиану треугольника по координатам его вершин, применим формулы координат середины отрезка и формулу расстояния между точками.

Рассмотрим нахождение медианы на конкретном примере.

Дано: ΔABC,

1) Так как AF — медиана треугольника ABC, то F — середина BC.

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Определение медианы

Медиана треугольника — это отрезок, который соединяет вершину треугольника с
серединой противоположной стороны. Медиана делит противолежащую сторону пополам.
Основание медианы — это точка пересечения медианы со стороной треугольника.

На рисунке 1 изображены три медианы, делящие каждая свою противолежащую
сторону пополам. Медианы BF, AH, CE соответственно делят пополам свои
противолежащие стороны AC, CB, AB.

В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Три медианы делят треугольник на 6 равновеликих треугольников.

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
AB – самая короткая сторона, следовательно, медиана CD – самая длинная.

Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.

Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S_△ = 5 см 2 ⋅ 6 = 30 см 2 .

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Решение
Воспользуемся формулой, приведенной в свойстве 5:

У вас уже есть абонемент? Войти

На данном уроке мы рассмотрим применение векторов для решения различных геометрических задач, вспомним и докажем некоторые геометрические факты.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»

У вас уже есть абонемент? Войти

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»

источники:

http://b4.cooksy.ru/articles/vektor-i-treugolnik-i-mediana

http://interneturok.ru/lesson/geometry/8-klass/vektory/primenenie-vektorov-k-resheniyu-zadach

Источник

Ответ на первый ответ постой:

Скалярное произведение есть скаляр, равный произведению модулей на косинус угла между ними:

А=|p|*|q|*cos(p, q) = 3 *1* cos (pi/3) = 3*0,5=1,5..

Со вторыми заданиями немного сложнее:

Сначала установим условно вектор q на оси х, тогда получим, что оба вектора начинаются в 0 и имеют между собой заданный угол..

Разложим оба вектора p и q на взаимно ортогональные составляющие:

px=|p|cos (п/3)=3*0,5=1,5

py=|p|sin (п/3)=3*0,86=2,6

qx=|q|=1

qy=0

Далее согласно заданным выражениям AB = 2p — q; AC = 3p + 2q произведём вычисления для каждой спроецированной компоненты..

AB = 2p — q; AC = 3p + 2q

АВх=2*1,5-1=2

АВу=2*2,6=5,2

АСх=3*1,5+2=6,5

АСу=3*1,5=4,5

Итак, мы задали точку А(0;0), получили точки В(2;5,2) С(6,5;4,5)..

Вектор ВС задаётся точкой А и В..

Теперь всё просто: находим длину отрезка ВС по известным координатам:

|BC|=sqrt((6,5-2)^2+(5,2-4,5)^2)= 4,5..

отношение cos a=(5,2-4,5)/4,5 есть угол относительно оси абсцисс, относительно которой мы и отсчитываем угол а=81 град=1,41 рад..

Модуль и угол задают вектор ВС..

Чтобы найти длину медианы нужно найти точку М, которая делит ВС напополам 4,5/2 = 2,25..

Из подобия прямоугольного треугольника, построенного на точек М стороны

(6,5-2)/2+2 = 4,25..

(5,2-4,5)/2+4,5= 4,85..

Это координаты точки М (4,25;4,85)..

Теперь находим АМ=sqrt((4,25)^2+(4,85)^2)=6,45..

Это и есть искомая длина медианы..

Источник

5. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1

ВЕКТОРНАЯ АЛГЕБРА

1. Векторы, базисы, координаты

№	Задание	Ответ
В треугольнике ABC разложите биссектрису CC по
	CB и b CA .
базису векторов a
РЕШЕНИЕ:

Пусть a CB , b CA ,
C лежит на стороне AB .

CC a b a ,

где a

Воспользуемся свойством биссектрисы треугольника

и тем, что BA BC C A. Отсюда

C A

следует, что

C A

CC 1 a

Докажите, что точка пе-

ресечения медиан тре-

угольника делит каждую

медиану в отношении

2 :1, считая от вершины.

РЕШЕНИЕ:


Пусть A – середина стороны BC , B	– середина
стороны AC . Отложим на медиане BB расстояние
	2	BB ‘		от вершины и поставим точку O . Тогда

3
		2		2

			AO AB		BB AB	BA AB
			3	3

1 AB 1 AC .

3 3

Отложим от вершины A по медиане AA	расстояние
	2	AA‘		и поставим точку M . Найдем координаты

3

вектора AM в базисе векторов AB и AC .
			2		2			1			2	1
		AM			AA				AB					AB	BA AC

										BC
					3							2	3	3
							3
						1	1	1			1
							AB		AC
									,		.
					3	3
							3			3

Но это координаты вектора AO . Таким образом, точка O и точка M совпадают, это точка пересечения медиан, и она делит медианы AA и BB в отношении 2 :1, считая от вершины.

В треугольнике ABC через O обозначена точка пе-

ресечения медиан. Найдите сумму векторов

OA OB OC .

РЕШЕНИЕ:

Обозначим

AB c , BC a , AC b,

b a c .

Из рисунка по свойству медиан

получаем, что

A1 A B1B C1C

OA OB OC

c c

a c b 0.

Точки E и F – середины сторон AD и BC четырех-

угольника ABCD . Докажите, что EF

AB DC

4Выведите теорему о средней линии трапеции. РЕШЕНИЕ:

EF EA AB BF , EF ED DC CF ,

							1
		BF CF , EA ED , EF	AB DC	.
		2
Если ABCD — трапеция, сторо-

ны AB и CD параллельны, то-
гда
		1			1
	EF			AB DC		AB
	2	2

— свойство средней линии трапеции.

На стороне AB и диагонали AC параллелограмма

ABCD	взяты соответственно точки E и F так, что
	1		1
AE		AB и AF		AC .
n	n 1

Докажите, что точки E , F и D лежат на одной прямой и определите отношение отрезков EF и FD .

5 ДОКАЗАТЕЛЬСТВО:

Пусть AB a , AD

b .Тогда a b AC .

EF AF AE

(a b)

b .

n 1

n(n 1)

n 1

FD AD AF b

( a b )

b .

n 1

EF || FD , то есть точки E ,

Отсюда | EF |:| FD |

F , D лежат на одной прямой.

Задан тетраэдр OABC . В базисе из ребер OA , OB и

OC найдите координаты векто-

ра OF , где F – точка пересече-

ния медиан основания ABC .

РЕШЕНИЕ:

6 Воспользуемся правилом треугольни-

ка:OF OA AF OA

AK .

K – середина ребра CB ; точка F находится на рас-

стоянии

длины медианы от вершины A.

AK AB

										1
					AO	OB	BO	OC .

													2
Подставим AK в OF :
							2
				OF OA	AO OB	1	BO OC
				3	3
						2			2			1			1
				OA			OA		OB		OB			OC
				3	3	3
																3
	1												1
		OA OB	OC								1			1
					,		OF =		,	,				.
3
											3	3		3
	В пространстве заданы треугольники ABC и
	A B C ; M и M		– точки пересечения медиан
	этих треугольников соответственно. Разложите
	вектор MM	по базису векторов AA , BB , CC .

РЕШЕНИЕ:

Пусть N – середина стороны BC , N – середина стороны B C .

MM MA AA A M

	.
	Найдем:
						2
	MA						NA ; NA	NB BA;
	3
														2	1	1		1
					1
	NB						CB ; M A	A M				N A ; N A N B B A ;

7										2							3				,	,
																	3	3	3
				1


	N B		2	C B ;

	C B C C CB BB ; B A B B BA AA .
	После последовательных подстановок		2
													2
	MM MA AA A M						NA AA

									N A
																3				3

				2
		NB BA AA	2	N	B B A
	3	3
				2								2	1
					1


				3 2						2				3 2
				2				1			1
							CB		BA AA			C C CB BB
	3		2	3	3
		2
		B B BA	AA	1	AA BB CC	,
	3	3

2. Декартов прямоугольный базис. Направляющие косинусы и координаты

В трапеции ABCD с основаниями AD и BC из-
вестны векторы
AB 2;2;5 ,
AC 3;6; 2 ,
AD 10;8; 14 . Найдите
сумму координат вектора					3
MN , где M и N — середины

сторон AB и CD .
РЕШЕНИЕ:
BC AC AB , MN	AD BC	AD AC AB	15	, 6,	21	.
2	2

2		2
3.
Даны точки A(8, 7, 4) , B(1, 2, 3) , C( 1, 1, 7) .
Найдите сумму координат точки D(x, y, z) , если
AB 2BC 3AD 0.
РЕШЕНИЕ:
AB 7,5,1 , BC 2,1, 4 ,	AD x 8, y 7, z 4 .

— 6

AB 2BC 3AD 0

7,5,1 4, 2,8 3x 24,3y 21,3z 12 0


	7 4 3x 24 0
		5 2 3y 21 0 (x, y, z) (9, 8, 7) .

		1 8 3z 12 0

	Сумма координат равна (- 6).
		2 и углы a 45 ,
	Дан модуль вектора	a

	b 60 и g 120 , которые он составляет с коор-
		2,1, 1
	динатными осями Ox , Oy и Oz соответственно.
	Вычислите проекции вектора a на координатные
	оси.

РЕШЕНИЕ:

ax a cosa 2cos 45 2 ;

ay a cosb 2cos60 1;

az a cosg 2cos120 1.

a = 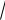2,1, 1

Даны векторы a												1, 1,		. Вы-
		2, 0, 1 и b		0
																							2b .
числите направляющие косинусы вектора a	cosa	0		,

РЕШЕНИЕ:																					5

																						2
																							cosb	,


																			5
a 2b 2, 0, 1 2 1, 1, 0		0, 2, 1 .
				1

				2			2			2
	a 2b		0		2		1	5 .								cos g

												5
cosa	0		; cosb	2		;	cos g	1	.


5								5					5
Может ли вектор составлять с координатными осями
следующие углы: a 45 , b 60 , g 120 ?
РЕШЕНИЕ:
Для направляющих косинусов выполняется равенство
cos2 a cos2 b cos 2g 1. Проверим его справедли-	да
вость.
															2
																				2	2
2					2						2			2		1	1

cos 45 cos	60 cos	120									1,


														2		2		2

равенство выполняется.

Даны точки A 3, 1, 5 , B 4, 2, 5 , C 4, 0, 3 .

Найдите длину медианы AA треугольника ABC .

РЕШЕНИЕ:							7

Координаты точки A (середины	AA ) A	0,1, 1	,

AA		3,2, 6		,	AA	3 2 22 6 2 7 .

Коллинеарны ли векторы c1	и c2 , построенные на	нет
векторах a и b , если a 9, 5,	3 ,

5b ?

b 7, 1, 2 , c1

, c2

РЕШЕНИЕ 1:

2a b 2

9, 5, 3

7, 1, 2

25, 9, 8

3a 5b

3 9, 5,

3 5

7, 1, 2

8, 20, 1

Пропорциональность компонент

c1y

c2 y

c2 z

c2 x

не выполняется, векторы неколлинеарны.

РЕШЕНИЕ 2

Векторы : a и b неколлинеарны, т.е. образуют базис. Векторы c1 и c2 неколлинеарны, так как их координаты в этом базисе не пропорциональны:

21 .

3. Скалярное произведение векторов

Найдите а)

a1 a2

и б)

3a1 2a2 , a1

2a2 , если

, a ,

РЕШЕНИЕ:

а)

a1 a2

, a1

а) 13 ,

, a1 a1,

a2 a2

a2 ,

б) 61

9 16

2 a1, a2

25 2

3 4cos

13.

б) 3a1

2a2 , a1 2a2

3a1 6 a1

, a2

2 a2 , a1 4a2

2π

3 9 4 a1,

a2 4 16 27 4 3 4 cos

64 61

Найдите

2a1 a2

, если a1 4, 2, 4 ,

a2 6, 3, 2 .

РЕШЕНИЕ:

105

2a1 a2 8, 4, 8 6, 3, 2 2, 1, 10 ,

105.

2a a

Найдите косинус угла между векторами AB и AC ,
	1,					0, 1,				3,
если A		2, 3	, B		2 ,	C	4, 5 .
РЕШЕНИЕ:
AB		0	1	, 1 2,						1, 1, 1 ,
	2 3		— 1
AC		2, 2, 2	,


								1 2	1	2 1	2


cos AB ,	AC					2					2	2

						12 1	12 2		22 2
1.

Вычислите синус угла, образованного векторами a 2, 2,1 и b 6, 3, 2 .

РЕШЕНИЕ:

Найдем косинус нужного угла:

cosj 2 6		2	3 1 2 12 6 2 4 ,
	5 17
	9 49			21		21		sinj
sin2 j 1 cos2 j 1	16		212 16		52 17	,	21

2	2	2
				21		21		21

sinj 517 . 21

Так как угол между векторами 0 j p,

sinj 517 . 21

Покажите, что

сумма квадратов

медиан треуголь-

ника относится к

сумме квадратов

b A

его сторон, как 3:4.

РЕШЕНИЕ:

b . Нахо-

Пусть CB a , CA b . Тогда

AB a

дим медианы треугольника:

a b

CC CB

BC a

b ,

BB BA AB

CA b

b .

Осталось найти требуемое отношение:

(ab)

2(ab)

Покажите, что четырехугольник ABCD

ромб, если

A(1,2,2) , B(3,5,8) , C( 3,2,6) , D( 5, 1,0).

Найдите угол при вершине А ромба.

РЕШЕНИЕ:

2, 3,

;

7 ;

;

p arccos

BC 6; 3; 2 ;

7 ;

;

7 .

и ABCD – ромб.

6 3

3 6

cos AB,

4 9 36

j p arccos

a, b

Докажите, что вектор

p b

перпендикуля-

рен вектору a .

РЕШЕНИЕ:

a, b

0 .

, a

a, b

Докажите: а) теорему косинусов; б) теорему Пифа-

гора.

ДОКАЗАТЕЛЬСТВО.

а) Рассмотрим треугольник

ABC , построенный на векто-

рах

AB и b

AC .

Пусть третья сторона

CB c .

Тогда

, a

cosg .

2 a,

б) При g 90

, получаем

теорему Пифагора.

Докажите, что диагонали ромба взаимно перпендикулярны.

РЕШЕНИЕ:

Пусть a AB и b AD –

стороны ромба.

b и

d1 AC a

d2 BD b

— его диагона-

ли.

a b

, b a

cos d1 , d2

так как для ромба

, и диагонали ромба

взаимно перпендикулярны.

4. Векторное произведение векторов

Найдите а)

a a

и б)

a 3a

3a a

если

2 , a ,

РЕШЕНИЕ:

а)

1 2 sin

3 ;

а) 3 ,

б)

б) 10 3

3 a1

a1 a1

a2 9 a2 a1 3 a2

10 a1 a2 10 3,

a1 a2 a2 a1

так как a1

a2 a2 0,

Найдите

, если

2a1

, 2a1

3, 1, 2

, a

1, 2, 1 .

РЕШЕНИЕ:

b 4 a1,

a2, a2

2 a1, a2

2 a2

4 a1, a2

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

то есть MM =

Как найти медиану если даны координаты вершин треугольника?

Рассмотрим нахождение медианы на конкретном примере.

Дано: ΔABC,

A(-11;12), B(3;8), C(-1;6),

AF — медиана.

Найти: AF

Решение:

1) Так как AF — медиана треугольника ABC, то F — середина BC.

По формулам координат середины отрезка:

$[x_F = frac{{x_B + x_C }}{2} = frac{{3 + ( - 1)}}{2} = 1;]$

$[y_F = frac{{y_B + y_C }}{2} = frac{{8 + 6}}{2} = 7.]$

Итак, F(1;7).

2) По формуле расстояния между точками

$[AF = sqrt {(x_F - x_A )^2 + (y_F - y_A )^2 } ]$

$[AF = sqrt {(1 - ( - 11))^2 + (7 - 12)^2 } = ]$

$[= sqrt {12^2 + ( - 5)^2 } = sqrt {144 + 25} = sqrt {169} = 13.]$

Ответ: 13.

Источник