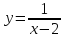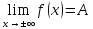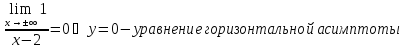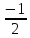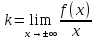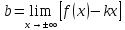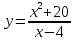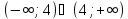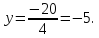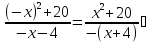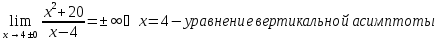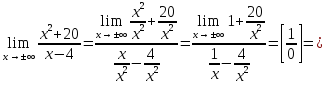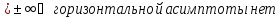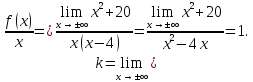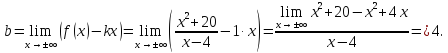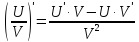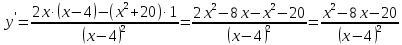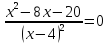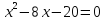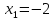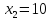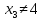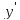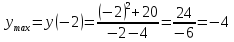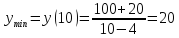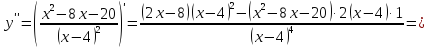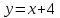Как найти меньшее значение функции на отрезке

Исследование функций и их графиков – это тема, которой уделяется особое внимание в рамках школьной программы старших классов. Некоторые основы математического анализа – дифференцирования – включены в профильный уровень экзамена по математике. У некоторых школьников возникают проблемы с этой темой, так как они путают графики функции и производной, а также забывают алгоритмы. В этой статье будут рассмотрены основные типы заданий и способы их решения.

Что такое значение функции?

Вам будет интересно:Проверочное слово к слову «скворец», корень и лексическое значение

Математическая функция представляет собой особое уравнение. Оно устанавливает взаимосвязь между числами. Функция зависит от значения аргумента.

Значение функции рассчитывается по заданной формуле. Для этого следует подставить любой аргумент, который соответствует области допустимых значений, в эту формулу на место х и выполнить необходимые математические операции. Какие?

Как можно найти наименьшее значение функции, используя график функции?

Вам будет интересно:Горизонтальный перенос генов: основы генетики, история открытия, принцип действия и примеры

Графическое изображение зависимости функции от аргумента называется графиком функции. Он строится на плоскости с определенным единичным отрезком, где по горизонтальной оси абсцисс откладывается значение переменной, или аргумента, а по вертикальной оси ординат – соответствующее ему значение функции.

Чем больше значение аргумента, тем правее он лежит на графике. И чем больше значение самой функции, тем выше находится точка.

О чем это говорит? Самым маленьким значением функции будет являться точка, которая лежит ниже всего на графике. Для того чтобы найти его на отрезке графика, нужно:

1) Найти и отметить концы этого отрезка.

2) Визуально определить, какая точка на этом отрезке лежит ниже всего.

3) В ответ записать ее числовое значение, которое можно определить, спроецировав точку на ось ординат.

Точки экстремума на графике производной. Где искать?

Вам будет интересно:Покои — это многозначное слово. Что именно оно означает?

Однако при решении задач иногда дан график не функции, а ее производной. Для того чтобы случайно не допустить глупую ошибку, лучше внимательно читать условия, так как от этого зависит, где нужно искать точки экстремума.

Итак, производная — это мгновенная скорость возрастания функции. Согласно геометрическому определению производная соответствует угловому коэффициенту касательной, которая непосредственно проведена к данной точке.

Известно, что в точках экстремума касательная параллельна оси Ox. Это значит, что ее угловой коэффициент — 0.

Из этого можно сделать вывод, что в точках экстремума производная лежит на оси абсцисс или обращается в ноль. Но кроме того, в этих точках функция меняет свое направление. То есть после периода возрастания начинает убывать, а производная, соответственно, сменяется с положительной на отрицательную. Или наоборот.

Если производная из положительной становится отрицательной — это точка максимума. Если из отрицательной становится положительной — точка минимума.

Важно: если в задании требуется указать точку минимума или максимума, то в ответ следует записать соответствующее значение по оси абсцисс. Но в случае, если требуется найти значение функции, то предварительно нужно подставить соответствующее значение аргумента в функцию и рассчитать его.

Как находить точки экстремума с помощью производной?

Рассмотренные примеры в основном относятся к заданию под номером 7 экзамена, которое подразумевает работу с графиком производной или первообразной. А вот задание 12 ЕГЭ – найти наименьшее значение функции на отрезке (иногда – наибольшее) – выполняется без каких-либо чертежей и требует базовых навыков математического анализа.

Для его выполнения нужно уметь находить точки экстремума с помощью производной. Алгоритм их нахождения таков:

• Найти производную от функции.
• Приравнять ее к нулю.
• Найти корни уравнения.
• Проверить, являются ли полученные точки точками экстремума или перегиба.

Для этого нужно начертить схему и на получившихся промежутках определить знаки производной, подставляя числа, принадлежащие отрезкам, в производную. Если при решении уравнения вы получили корни двойной кратности – это точки перегиба.

• Применив теоремы, определить какие точки являются точками минимума, а какие – максимума.

Вычисление наименьшего значения функции с применением производной

Однако, выполнив все эти действия, мы найдем значения точек минимума и максимума по оси абсцисс. Но как найти наименьшее значение функции на отрезке?

Что необходимо сделать для того, чтобы найти число, которому соответствует функция в конкретной точке? Нужно подставить в данную формулу значение аргумента.

Точки минимума и максимума соответствуют наименьшему и наибольшему значению функции на отрезке. Значит, чтобы найти значение функции, нужно рассчитать функцию, используя полученные значения х.

Важно! Если в задании требуется указать точку минимума или максимума, то в ответ следует записать соответствующее значение по оси абсцисс. Но в случае, если нужно найти значение функции, то предварительно следует подставить соответствующее значение аргумента в функцию и выполнить необходимые математические операции.

Что делать, если на данном отрезке отсутствуют точки минимума?

Но как найти наименьшее значение функции на отрезке, на котором отсутствуют точки экстремума?

Это значит, что на нем функция монотонно убывает или возрастает. Тогда в функцию нужно подставить значение крайних точек этого отрезка. Есть два пути.

1) Рассчитав производную и промежутки, на которых она положительна или отрицательна, сделать вывод о том, убывает функция на данном отрезке или возрастает.

В соответствии с ними подставить в функцию большее или меньшее значение аргумента.

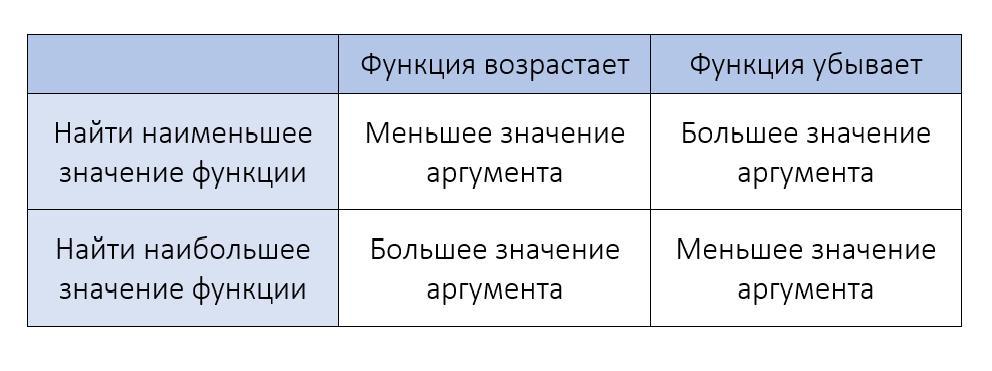
2) Просто подставить в функцию обе точки и сравнить полученные значения функции.

В каких заданиях нахождение производной необязательно

Как правило, в заданиях ЕГЭ все же нужно находить производную. Есть только пара исключений.

1) Парабола.

Вершина параболы находится по формуле.

Если a < 0, то ветви параболы направлены вниз. И ее вершина является точкой максимума.

Если a > 0, то ветви параболы направлены вверх, вершина – точка минимума.

Рассчитав точку вершины параболы, следует подставить ее значение в функцию и вычислить соответствующее значение функции.

2) Функция y = tg x. Или y = ctg x.

Эти функции являются монотонно возрастающими. Поэтому, чем больше значение аргумента, тем больше значение самой функции. Далее мы рассмотрим, как найти наибольшее и наименьшее значение функции на отрезке с примерами.

Основные типы заданий

Задание: наибольшее или наименьшее значение функции. Пример на графике.

На рисунке вы видите график производной функции f (x) на интервале [-6; 6]. В какой точке отрезка [-3; 3] f (x) принимает наименьшее значение?

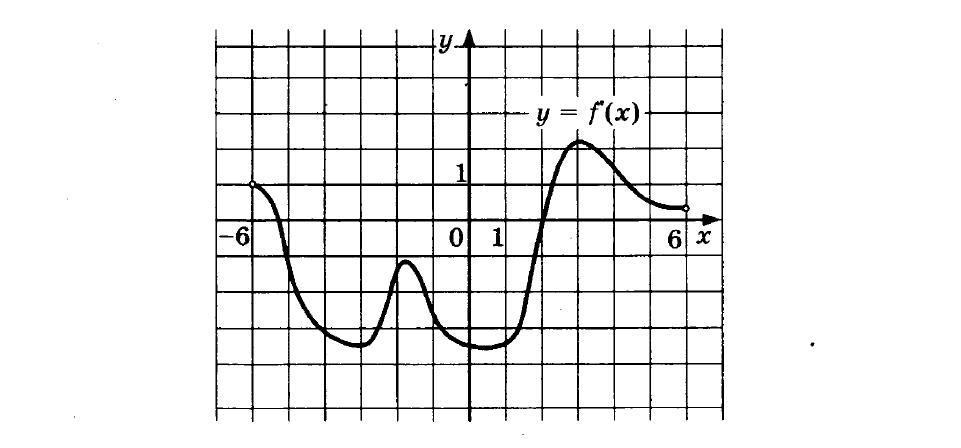
Итак, для начала следует выделить указанный отрезок. На нем функция один раз принимает нулевое значение и меняет свой знак – это точка экстремума. Так как производная из отрицательной становится положительной, значит, это точка минимума функции. Этой точке соответствует значение аргумента 2.

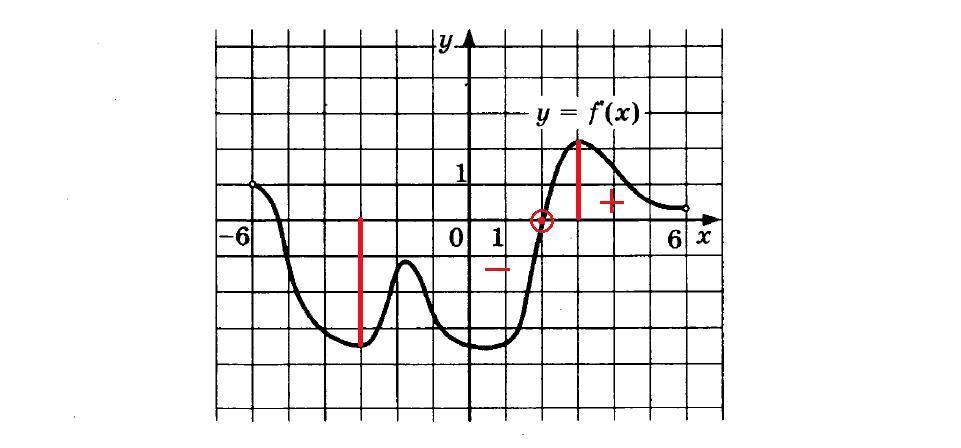
Ответ: 2.

Продолжаем рассматривать примеры. Задание: найти наибольшее и наименьшее значение функции на отрезке.

Найдите наименьшее значение функции y = (x — ex-7 на отрезке [6; 8].

1. Взять производную от сложной функции.

y’ (x) = (x — ex-7 = (x — 8)’ (ex-7) + (x — (ex-7)’ = 1 * (ex-7) + (x — (ex-7) = (1 + x — (ex-7) = (x — 7) (ex-7)

2. Приравнять полученную производную к нулю и решить уравнение.

y’ (x) = 0

(x — 7) (ex-7) = 0

x — 7 = 0, или ex-7 = 0

x = 7; ex-7 ≠ 0, нет корней

3. Подставить в функцию значение крайних точек, а также полученные корни уравнения.

y (6) = (6 — e6-7 = -2e-1

y (7) = (7 — e7-7 = -1 * e0 = -1 * 1 = -1

y (8) = (8 — e8-7 = 0 * e1 = 0

Ответ: -1.

Итак, в этой статье была рассмотрена основная теория о том, как найти наименьшее значение функции на отрезке, необходимая для успешного решения заданий ЕГЭ по профильной математике. Также элементы математического анализа применяются при решении заданий из части С экзамена, но очевидно, они представляют иной уровень сложности, и алгоритмы их решений сложно уместить в рамки одного материала.

Как найти наибольшее и наименьшее значения функции на отрезке?

Для этого мы следуем известному алгоритму:

1. Находим ОДЗ функции.

2. Находим  производную функции

3. Приравниваем производную  к нулю

4. Находим промежутки, на которых производная сохраняет знак,  и по ним определяем промежутки возрастания и убывания функции:

Если на промежутке I производная функции , то функция возрастает на этом  промежутке.

Если на промежутке I производная функции , то функция убывает на этом промежутке.

5. Находим точки максимума и минимума функции.

В точке максимума функции производная меняет знак с «+» на «-«.

В точке минимума функции производная меняет знак с «-» на «+».

6. Находим значение функции в концах отрезка,

• затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
• или   сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции

Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.

Рассмотрим функцию . График этой функции выглядит так:

В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.

1. Рассмотрим функцию на отрезке

Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: , а наименьшее — в левом: .

2. Рассмотрим функцию на отрезке

Очевидно, что наибольшее значение функция принимает в точке максимума , а наименьшее — в одном из концов отрезка, то есть надо найти значения и и выбрать из них наименьшее.

3. Если мы рассмотрим функцию на отрезке , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть  и .

Чтобы найти наименьшее значение функции,  нам нужно будет сравнить значения функции в точке минимума  и в левом конце отрезка, то есть  и .

Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:

1. ОДЗ функции  — множество действительных чисел.

2. 

3. , если  или

Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание — убывание, можно схематично изобразить ее график:

Рассмотрим несколько примеров решения задач из  Открытого банка заданий для подготовки к ЕГЭ  по математике

1. Задание B15 (№ 26695)

Найдите наибольшее значение функции   на отрезке .

1. Функция определена при всех действительных значениях х

2.

3. 

Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция  возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.

y(0)=5

Ответ: 5.

2. Задание B15 (№ 26702)

Найдите наибольшее значение функции   на отрезке [].

1. ОДЗ функции  

2. 

Производная равна нулю при , однако, в этих точках она не меняет знак:

, следовательно, , значит, , то есть производная при всех допустимых значених х неотрицательна, следовательно, функция  возрастает и принимает наибольшее значение в правом конце промежутка, при .

Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:

у(0)=5

Ответ: 5.

3. Задание B15 (№ 26708)

Найдите наименьшее значение функции   на отрезке [].

1.  ОДЗ функции :

2. 

3.

, 

Расположим корни этого уравнения на тригонометрической окружности.

Промежутку  принадлежат два числа:  и 

Расставим знаки. Для этого определим знак производной в точке х=0: . При переходе через точки  и  производная меняет знак.

Изобразим смену знаков производной функции  на координатной прямой:

Очевидно, что точка  является точкой минимума ( в ней производная меняет знак с «-» на «+»), и чтобы найти наименьшее значение функции  на отрезке , нужно сравнить значения функции в точке минимума и в левом конце отрезка, .

Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а  таковым на является, следовательно подставим в уравнение функции 

Ответ: -1

И.В. Фельдман, репетитор по математике.

Наибольшее и наименьшее значение функции

Как найти?

Постановка задачи

Найти наибольшее и наименьшее значение функции $ f(x) $ на отрезке $ [a,b] $

План решения

Наибольшее и наименьшее значение непрерывной функции $ f(x) $ на промежутке $ [a,b] $ достигаются в критических точках, то есть в точках в которых производная функции равна нулю $ f'(x) = 0 $, бесконечности $ f'(x) = pm infty $, не существует, либо на концах отрезка $ [a,b] $

1. Проверяем на непрерывность функцию $ f(x) $ на заданном отрезке
2. Если функция непрерывная, то находим производную $ f'(x) $ и приравниваем её к нулю
3. Решая уравнение $ f'(x) = 0 $ получаем корни, являющиеся критическими точками
4. Выбираем критические точки, принадлежащие отрезку $ [a,b] $
5. Вычисляем значения функции $ f(x) $ в оставшихся критических точках, а так же на концах промежутка $ [a,b] $. Затем выбираем из них наибольшее $ M $ и наименьшее $ m $

Примеры решений

Пример 1

Найти наибольшее и наименьшее значение функции $ y = 2x^3 — 3x^2 — 4 $ на отрезке $ [0;2] $

Решение

Функция представляет собой кубический многочлен. Точек разрыва нет, значит функция непрерывна на отрезке $ [0;2] $. Находим производную: $$ y’ = (2x^3 — 3x^2 — 4)’ = 6x^2 — 6x $$ Приравниваем производную к нулю. Решаем уравнение и получаем критические точки: $$ 6x^2 — 6x = 0 $$ $$ 6x(x — 1) = 0 $$ $$ x_1 = 0, x_2 = 1 $$ Проверяем принадлежность полученных точек отрезку $ [0;2] $: $$ x_1 in [0;2], x_2 in [0;2] $$ Так как обе точки принадлежат отрезку, то вычисляем в них значение функции $ f(x) $, так же значение этой функции на концах интервала $ [0;2] $: $$ y(x_1) = y(a) = f(0) = 2 cdot 0^3 — 3 cdot 0^2 — 4 = -4 $$ $$ y(x_2) = y(1) = 2 cdot 1^3 — 3 cdot 1^2 — 4 = -5 $$ $$ y(b) = y(2) = 2 cdot 2^3 — 3 cdot 2^2 — 4 = 0 $$ Среди полученных значений наибольшее $ M = 0 $, наименьшее $ m = -5 $ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ M = 0, m = -5 $$

Пример 2

Найти наименьшее и наибольшее значение функции $ y = frac{4x^2}{3+x^2} $ на $ [-1;1] $

Решение

Функция непрерывна на $ x in [-1;1] $ так как знаменатель не обращается в ноль ни при каком $ x $. Выполняем нахождение производной: $$ y’ = (frac{4x^2}{3+x^2})’ = frac{(4x^2)'(3+x^2)-(4x^2)(3+x^2)’}{(3+x^2)^2} = $$ $$ = frac{8x(3+x^2)-(4x^2)(2x)}{(3+x^2)^2} = frac{24x+8x^3-8x^3}{3+x^2)^2} = frac{24x}{(3+x^2)^2} $$ Приравниваем полученную производную к нулю и вычисляем критические точки: $$ frac{24x}{(3+x^2)^2} = 0 $$ $$ 24x = 0, 3+x^2 neq 0 $$ $$ x = 0 $$ Получена единственная критическая точка $ x = 0 $, которая принадлежит $ [-1; 1] $. Вычисляем значение функции $ f(x) $ в критической точке и на концах интервала $ [-1;1] $: $$ y(-1) = frac{4cdot (-1)^2}{3+(-1)^2} = frac{4}{4}=1 $$ $$ y(0) = frac{0}{3} = 0 $$ $$ y(1) = frac{4cdot 1^2}{3+1^2} = frac{4}{4} = 1 $$ Из полученных значений видно, что максимальное значение $ M = 1 $ и минимальное значение $ m = 0 $.

Ответ

$$ m = 0, M = 1 $$

Наибольшее и наименьшее значение функции на отрезке.

Пусть
функция у =
f
(х) непрерывна
на отрезке [a,
b]. Как
известно, такая функция на этом отрезке
достигает наибольшего и наименьшего
значений. Эти значения функция может
принять либо во внутренней точке отрезка
[a, b],
либо на границе отрезка.

Для
нахождения наибольшего и наименьшего
значений функции на отрезке [a,
b] необходимо:

1)найти
критические точки функции в интервале
(a, b);

2)вычислить
значения функции в найденных критических
точках;

3)
вычислить значения функции на концах
отрезка, то есть при x=
а и х =
b;

4)из
всех вычисленных значений функции
выбрать наибольшее и наименьшее.

Пример.
Найти наибольшее и наименьшее значения
функции

на
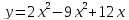
отрезке [0; 3].

Находим
критические точки:

Эти
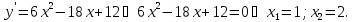
точки лежат внутри отрезка [0; 3]; y(1)
= ‒ 3; y(2)
= ‒ 4; y(0)
= ‒ 8; y(3)
= 1;

в
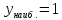
точке x =
3 и
в точкеx =
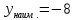
0.

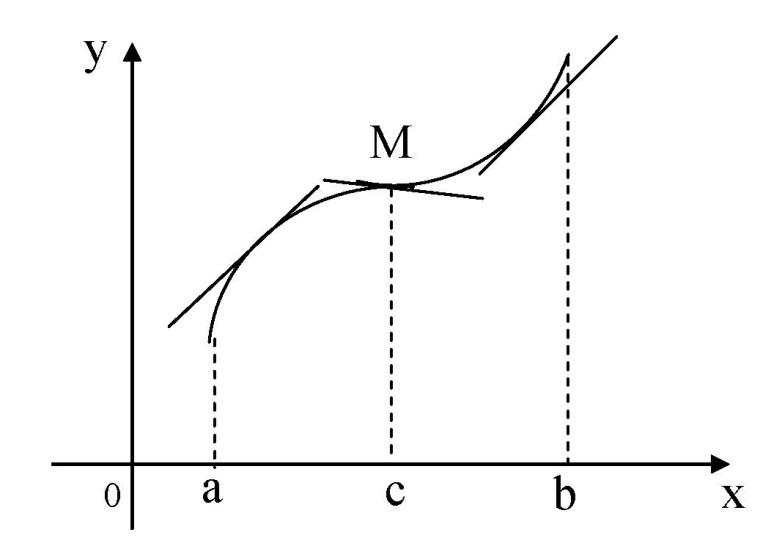
Исследование функции на выпуклость и точку перегиба.

Функция
y
= f
(x)
называется
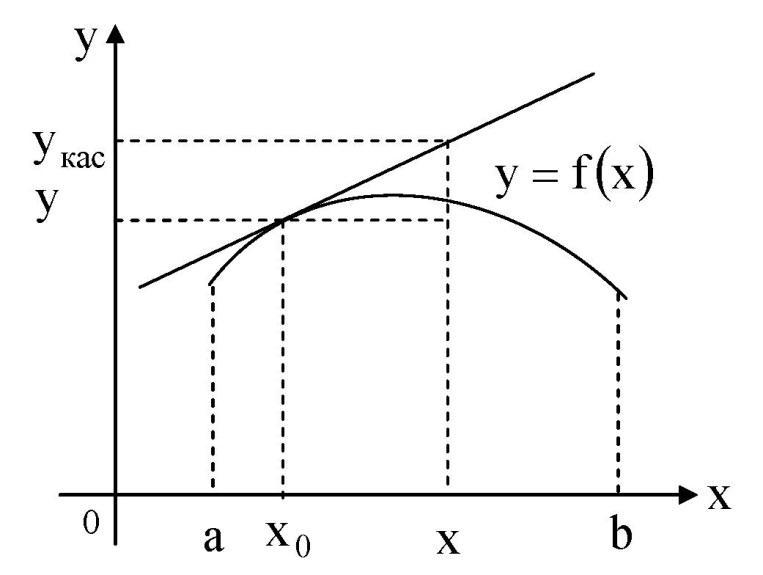
выпуклойвверх
на промежутке (a,
b),
если ее график лежит под касательной,
проведенной в любой точке этого
промежутка, и называется выпуклой
вниз (вогнутой),
если ее график лежит над касательной.

Точка,
при переходе через которую выпуклость
сменяется вогнутостью или наоборот,
называется точкой
перегиба.

Алгоритм
исследования на выпуклость и точку
перегиба:

1.
Найдем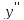и критические точки второго рода, то
есть точки в которых вторая производная
равна нулю или не существует.

2.
Нанести критические точки на числовую
прямую, разбивая ее на промежутки. Найти
знак второй производной на каждом
промежутке; если
,
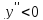
то функция выпуклая вверх, если,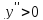
то функция выпуклая вниз.

3.
Если при переходе через критическую
точку второго рода
поменяет знак и в этой точке вторая
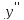
производная равна нулю, то эта точка ‒
абсцисса точки перегиба. Найти ее
ординату.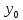

Рис.13

Рис.14

Асимптоты графика функции. Исследование функции на асимптоты.

Определение.
Асимптотой
графика функции называется прямая,
обладающая тем свойством, что расстояние
от любой точки графика до этой прямой
стремится к нулю при неограниченном
удалении точки графика от начала
координат.

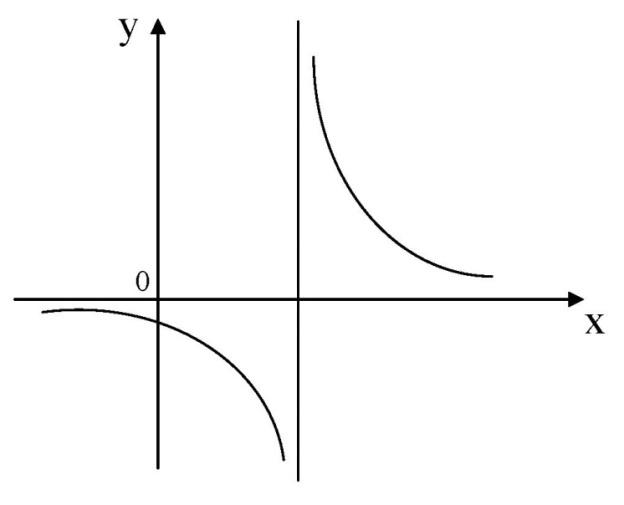
Рис.15

Существуют
три вида асимптот: вертикальные,
горизонтальные и наклонные.

Определение.
Прямая
называетсявертикальной
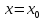
асимптотой графика
функции у =
f (х), если
хотя бы один из односторонних пределов
функции в этой точке равен бесконечности,
то есть

где

‒ точка разрыва функции, то естьне принадлежит области определения.

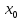
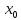
Пример.

D
(y)
= (‒ ∞; 2)
(2; + ∞)

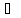
x=
2 ‒ точка разрыва.

Определение.
Прямая у
= A
называется горизонтальной
асимптотой
графика функции у
= f(х) при
,
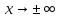
если

Пример.

x	0	3	1
y		1	‒ 1

Определение.
Прямая у
= kх
+ b
(k≠
0) называется наклонной
асимптотой
графика функции у
= f (х) при
,
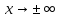
где

Общая схема исследования функций и построения графиков.

Алгоритм
исследования функции у
= f (х):

1.
Найти область определения функцииD
(y).

2.
Найти (если это можно) точки пересечения
графика с осями координат (при x
= 0 и при y
= 0).

3.
Исследовать на четность и нечетность
функции(y
(‒x)
= y
(x)
‒четность;
y(‒x)
= ‒y
(x)
‒нечетность).

4.
Найти асимптоты графика функции.

5.
Найти интервалы монотонности функции.

6.
Найти экстремумы функции.

7.
Найти интервалы выпуклости (вогнутости)
и точки перегиба графика функции.

8.
На основании проведенных исследований
построить график функции.

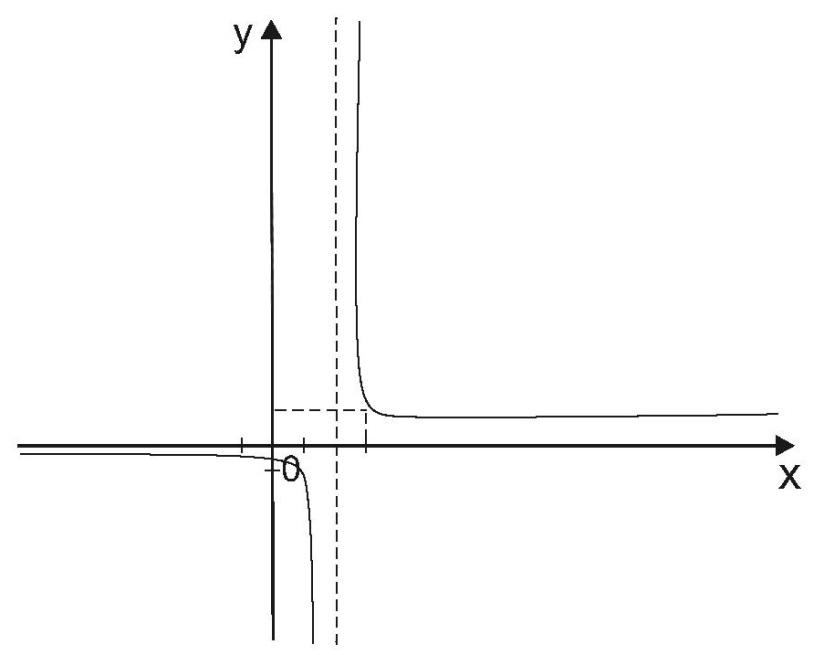
Пример.
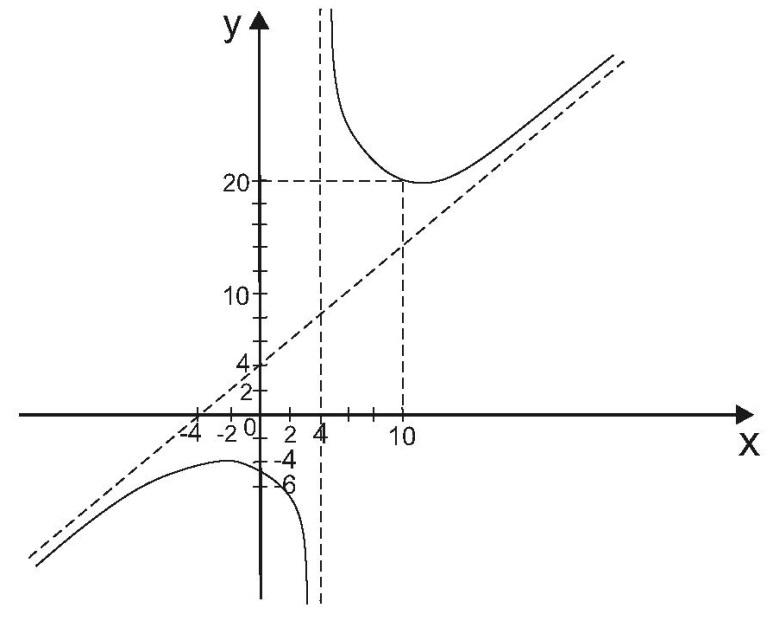
Исследовать
функцию и построить ее график.

1)
D
(y)
=

x
= 4 ‒ точка разрыва.

2)
При x
= 0,

(0;
‒ 5) ‒ точка пересечения с oy.

При
y
= 0,

3)
y(‒
x)=

функция общего вида (ни четная, ни
нечетная).

4)
Исследуем на асимптоты.

а)
вертикальные

б)
горизонтальные

в)
найдем наклонные асимптоты
где

‒уравнение
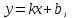
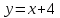
наклонной асимптоты

5)
В данном уравнении не требуется найти
интервалы монотонности функции.

6)

Эти
критические точки разбивают всю область
определения функции на интервале (˗∞;
˗2), (˗2; 4), (4; 10)и (10; +∞). Полученные результаты
удобно представить в виде следующей
таблицы:

x	(˗∞; ˗2)	˗2	(˗2; 4)	4	(4; 10)	10	(10; +∞)
	+	0	˗	0	˗	0	+
y		max		нет экстр.		min

Из
таблицы видно, что точках
= ‒2‒точка
максимума, в точкех
= 4‒нет экстремума, х
= 10 ‒точка минимума.

Подставим
значение (‒ 3) в уравнение:

9
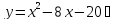
+ 24 ‒ 20 > 0

0
‒ 20 < 0

25
‒ 40 ‒ 20 < 0

121
‒ 88 ‒ 20 > 0

Максимум
этой функции равен

(‒
2; ‒ 4) ‒ экстремум максимальный.

Минимум
этой функции равен

(10;
20) ‒ экстремум минимальный.

7)
исследуем на выпуклость и точку перегиба
графика функции

x	0	4
y	4	8

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Математики и Data Science-специалисты должны хорошо разбираться в функциях. Предлагаем попрактиковаться в решении задач на обнаружение максимальных и минимальных значений у заданных функций.

Максимум

Задумываясь над тем, как найти максимальное значение функции, нужно четко понимать, с чем предстоит иметь дело. Для этого нужно запомнить такое определение:

Наибольшее значение функции y = f(x) на промежутке x – это max y = f(x₀). Оно будет при любом значении x€ X, x≠x₀ делает справедливым неравенство: f(x)≤f(x₀).

Максимальное значение (максимум) – это точка на функции, в которой значение функции больше, чем в соседних «отметках».

Минимум

Наименьшее значение функции находить так же легко, как и наибольшее. Но сначала нужно понимать, что это такое.

Значение функции на отрезке будет считаться минимумом, если оно меньше, чем в соседних «отметках». Здесь действует такое определение:

Наименьшее значение функции y=f(x) на промежутке x – это miny=f(x₀), которое при любом значении x€ X, x≠x₀ делает справедливым неравенство f(x)≥f(x₀).

Соответствующие определения являются достаточными и очевидными. Если говорить простыми словами, то максимум функции – это ее самое большое значение на заданном промежутке (участке) при абсциссе x₀, а минимум – самое маленькое.

Стационарные точки

При решении вопроса о том, как найти наибольшее или наименьшее значение функции, стоит обратить внимание на так называемые «стационарные точки». Это – значения аргумента функции, при которых ее производная будет равняться нулю.

Стационарная точка – это «отметка», в которой расположен экстремум дифференцируемой функции. А именно – локальный минимум или максимум. В одной из таких «отметок» записанное выражение будет достигать своих предельных параметров.

Здесь рекомендуется запомнить следующее:

1. Экстремум функции – это минимумы и максимумы.
2. Если определить производную в точках экстремумов, она будет равно 0.
3. Когда говорят «экстремумы», подразумевается значение функции. Если же речь идет об «отметках» экстремумов, рассматривать стоит x, в которых достигаются соответствующие пределы.

 Этого достаточно для того, чтобы разобраться, как найти наибольшее на заданном отрезке у выражения. Для реализации поставленной задачи вовсе не обязательно составлять график. Поэтому сначала воспользуемся записями формул и вычислений.

План действий

Пример – дана функция f(x) на отрезке [a, b]. Наибольшее и наименьшее значение такой непрерывной функции достигаются в определенных местах. Это – критические точки. Там, где производная записанного выражения будет равно нулю.

Для того, чтобы найти наибольшие значения уравнения, потребуется придерживаться следующего алгоритма:

1. Узнайте, какая перед вами функция. Для этого нужно проверить ее на непрерывность. В расчет обязательно берется заданный отрезок.
2. Если запись непрерывная – ищем производную.
3. После того, как найдем производную, приравниваем ее к нулю. Это поможет найти точки экстремумов. В результате получаются корни.
4. Образовавшиеся корни – это критические точки. Нужно выбрать те «параметры», что относятся к промежутку [a, b].
5. Вычислить значения функции на концах отрезка [a, b].
6. Определить значения имеющегося выражения в критических «отметках».

Теперь понятно, как найти наибольшие функции на заданном отрезке. После произведенных подсчетов остается выбрать из результатов M (максимум) и m (минимум).

На отрезке

Разобравшись в тем, как найти наибольшие «параметры» выражения «на бумаге», стоит рассмотреть соответствующий процесс на графиках. Определять максимумы/минимумы в данном случае будет проще.

Первый график указывает на выражение, у которого точка минимума и максимума находятся в стационарных точках на промежутке [-6;6]. Соответствующие «пределы» обозначены жирным.

Второй график указывает на изменение отрезка. Теперь он будет [1;6]. Минимальное значение останется прежним. А вот максимальное – изменится. Оно образуется в правой части в точке с абсциссой. Поиск минимального «параметра» окажется в критической точке.

Задумываясь, как найти наименьшие или «самые крупные» параметры выражения на графике, можно также рассмотреть третий рисунок. Здесь функция принадлежала промежутку [-3;2]. Чтобы найти наибольшее и наименьшее в таком случае, предстоит учитывать абсциссы. В них достигаются соответствующие пределы.

Открытый интервал

Если промежуток задан конкретным числом, определить экстремумы будет не так сложно. Иначе происходит, если интервал открыт.

Здесь:

1. Функция будет принимать максимум/минимум по значению в стационарных точках на открытом интервале от -6 до 6. Ответ – на 4 рисунке.
2. Если взять отрезок [1;6), минимум будет достигнут в стационарной точке. А вот максимум – неизвестен. Связано это с тем, что 6 не принадлежит к заданному интервалу. Если бы «шестерка» относилась к соответствующему промежутку, ответ на вопрос относительно определения максимума оказался понятным. Максимальный параметр был бы в точке с абсциссой 6.
3. На рисунке 6, задумываясь, как найти наименьшие «параметры», нужно обратить внимание на заданный интервал. Он равен (-3;2]. Минимум будет достигнут в правой границе. А вот максимум – не определен.

Найти значения на графиках обычно проще, чем «в чистых формулах». Соответствующие задания можно отыскать тут.

Бесконечность

Иногда значения функций нужно найти на бесконечном промежутке. Графически возможны такие ситуации:

На 7 рисунке функция достигает максимума в стационарной точке с абсциссой 1. Минимум окажется на границе интервала справа. На минус бесконечности значения приближаются к y=3 асимптотически.

Если взять интервал от 2-х до «плюс бесконечности», заданная функция не будет иметь ни максимумов, ни минимумов. Значения здесь стремятся к бесконечности. Связано это с тем, что x=2 является вертикальной асимптотой. Если абсцисса стремится к плюс бесконечности, значения будут асимптотически подходить к y=3. Соответствующий пример показан на рисунке 8.

Чтобы не приходилось долго разбираться с тем, как найти наименьшее у заданной функции, не путаться с тем, какие знаки производной использовать, а также легко строить графики, можно воспользоваться специальными онлайн калькуляторами. А еще – закончить тематические дистанционные онлайн курсы.