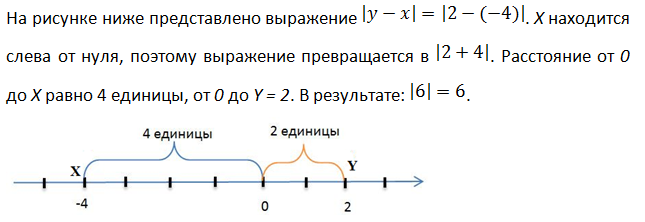
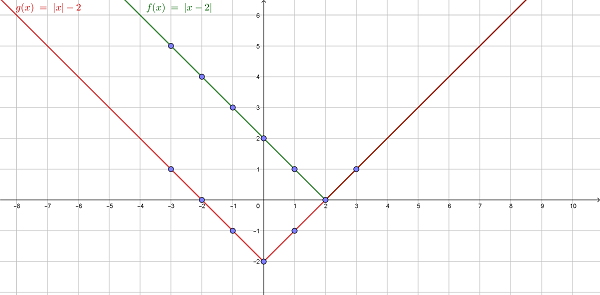
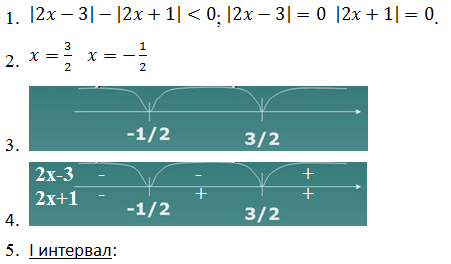
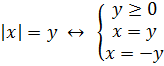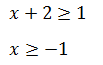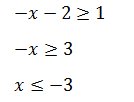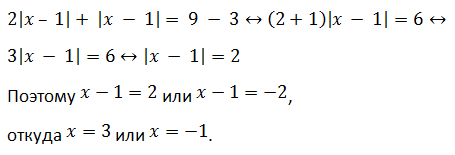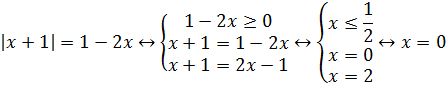Модуль
В этой статье введем и очень подробно разберем такое важное понятие, как модуль числа. Разберемся, откуда модуль взялся, какими свойствами обладает. Научимся решать уравнения и неравенства с модулем.
«Величина» числа
Сначала попытаемся сформулировать понятие о «величине» числа. Из этого понятия естественным образом получим понимание, откуда взялся и как определить модуль.
Геометрический смысл
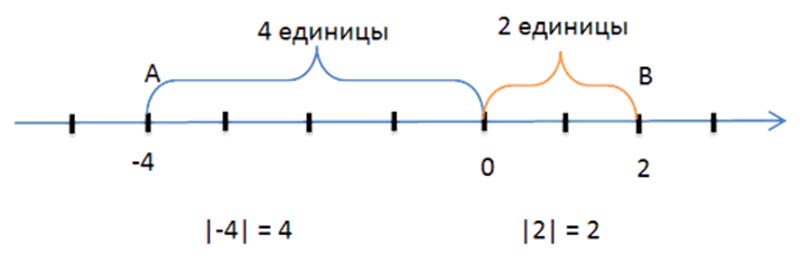
Представьте, что вы стоите в точке 0 на числовой оси. Слева от вас, в точке − 1 0 0 , находится школа. Справа, в точке 5 0 , находится ваш дом. Математически число − 1 0 0 меньше, чем 5 0 . Но вот идти до школы 1 0 0 метров влево гораздо дольше, чем пройти 5 0 метров до дома вправо. В этом смысле «величина» пройденного расстояния в − 1 0 0 метров больше, чем 5 0 метров.
Пусть теперь школа находится в точке − 1 0 , а дом в точке 1 0 . Математически вновь получаем, что − 1 0 меньше 1 0 . Но вот нам, находящимся в 0 , совершенно нет разницы: идти − 1 0 метров влево или 1 0 метров вправо. В обоих случаях мы пройдем 1 0 метров. То есть, по «величине» числа − 1 0 и 1 0 равны.
Количественный смысл
Рассмотрим числа 5 0 и − 1 0 0 . В математическом смысле − 1 0 0 гораздо меньше 5 0 . А давайте посмотрим на эти числа под другим углом. У вас есть всего 5 0 рублей и вы задолжали другу. Ваш долг составляет − 1 0 0 рублей. В этом смысле «величина» вашего долга в − 1 0 0 рублей гораздо больше имеющихся у вас 5 0 рублей. Получается, что математически − 1 0 0 меньше 5 0 , но по «величине» − 1 0 0 больше 5 0 .
Теперь рассмотрим числа − 1 0 и 1 0 . Математически, опять же, − 1 0 меньше 1 0 . Но, пользуясь нашей аналогией с долгом, своими 1 0 рублями вы полностью покроете долг в − 1 0 рублей. То есть, по «величине» число − 1 0 равно числу 1 0 .
Понятие величины
Мы поняли, что каждое число имеет свою «величину». Причем эта величина не зависит от того, положительным или отрицательным является число. Можно даже сказать, что «величина» числа это и есть само число, от которого «отбросили» его знак.
Модуль числа
Сформулируем на строгом языке математики наше интуитивное представление о «величине» числа, которое мы сформировали в предыдущем разделе.
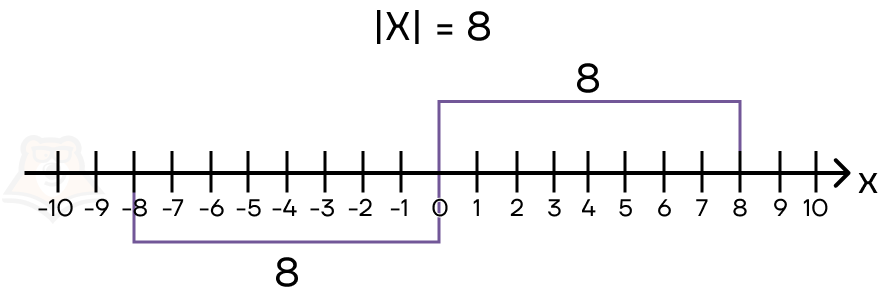
Модуль или абсолютная величина вещественного числа x — само число x , если оно неотрицательно, иначе − x .
Допустим, мы хотим найти модуль какого-то числа a . Согласно определению, нам надо провести элементарную проверку. Если число a положительное или равно 0 , то модулем a и является само a . Если же a меньше 0 , то результатом модуля будет − a .
∣ 5 ∣ = 5 ∣ 0 ∣ = 0 ∣ − 1 2 ∣ = − ( − 1 2 ) = 1 2
Легко убедиться, что модуль числа полностью соответсвует по смыслу «величине» числа, рассмотренной в предыдущем разделе. Там мы утверждали, что по «величине» − 1 0 0 больше 5 0 , а − 1 0 равно 1 0 . И действительно:
∣ − 1 0 0 ∣ = 1 0 0 ∣ − 1 0 ∣ = 1 0 ∣ 5 0 ∣ = 5 0 ∣ − 1 0 0 ∣ > ∣ 5 0 ∣ ∣ 1 0 ∣ = 1 0 ∣ − 1 0 ∣ = ∣ 1 0 ∣
Положение знака нестрогого неравенства в определении модуля не имеет значения:
Обозначим второе определение модуля числа x как ∣ x ∣ ′ . Покажем, что какой x не возьми, будет выполняться ∣ x ∣ = ∣ x ∣ ′ .
Пусть x > 0 . По классическому определению ∣ x ∣ = x . По второму: ∣ x ∣ ′ = x . То есть ∣ x ∣ = ∣ x ∣ ′ .
Пусть x = 0 . По классическому определению ∣ 0 ∣ = 0 . А вот во втором определении 0 попадает уже под второе условие, то есть ∣ 0 ∣ ′ = − 0 = 0 . Опять имеем ∣ 0 ∣ = ∣ 0 ∣ ′ .
Наконец, пусть x < 0 . По классическому определению ∣ x ∣ = − x . У второго определения та же ситуация: ∣ x ∣ ′ = − x . Получается, что и в этом случае ∣ x ∣ = ∣ x ∣ ′ .
Итак, мы рассмотрели все возможные значения для x и во всех случаях ∣ x ∣ = ∣ x ∣ ′ . Это и означает, что между двумя определениями нет никакой разницы ■
Такое определение иногда бывает полезно. Например, если x лежит в следующих пределах: − 1 0 ≤ x ≤ 0 , то можно сразу сказать, что ∣ x ∣ = − x , даже несмотря на то, что для x = 0 так выражаться будет некорректно, ведь ∣ 0 ∣ = 0 , а не − 0 .
Свойства модуля
У модуля есть очень много полезных свойств, которые сильно помогают при решении уравнений, неравенств, доказательстве теорем и так далее. Рассмотрим самые полезные из них. Все свойства ниже формулируем для любых вещественных чисел x и y .
Очевидные свойства
Наиболее очевидные свойства модуля напрямую вытекают из рассмотренного ранее понятия о «величине» числа. Например, мы определили «величину» числа как само число с «отброшенным» знаком. Это означает, что «величина» не может быть отрицательной.
Модуль числа — теория и решение задач
А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.
Ситуация первая
В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.
Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.
Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.
Ситуация вторая
Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.
И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?
Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.
Ситуация третья
В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.
А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.
Ну вот, ты уже почти все знаешь. Давай теперь подробнее…
Модуль числа — коротко о главном
Модуль (абсолютная величина) числа ( displaystyle x) — это само число ( displaystyle x), если ( displaystyle xge 0), и число ( displaystyle -x), если ( displaystyle x<0):
- Модуль числа есть число неотрицательное: ( left| x right|ge 0,textleft| x right|=0Leftrightarrow x=0);
- Модули противоположных чисел равны: ( left| -x right|=left| x right|);
- Модуль произведения двух (и более) чисел равен произведению их модулей: ( left| xcdot yright|=left| x right|cdot left|yright|);
- Модуль частного двух чисел равен частному их модулей: ( displaystyle left| fracright|=frac,textne text);
- Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:( left| x+y right|le left| x right|+left| y right|);
- Постоянный положительный множитель можно выносить за знак модуля: ( left| cx right|=ccdot left| x right|) при ( displaystyle c>0);
- Квадрат модуля числа равен квадрату этого числа: ( ^>=^>).
Кстати, в продолжение этой темы у нас есть отличная статья: «Уравнения с модулем«. Когда прочитаешь эту статью, обязательно ознакомься и со второй.
И просто чтобы ты знал, модуль часто попадается при решении квадратных уравнений или иррациональных.
Что же такое модуль числа?
Представь, что это ты.
Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления ( 0).
Итак, ты делаешь ( 3) шага вперёд и оказываешься в точке с координатой ( 3).
Это означает, что ты удалился от места, где стоял на (3) шага (( 3) единичных отрезка).
То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно ( 3).
Но ведь ты же можешь двигаться и назад!
Если от отправной точки с координатой ( 0) сделать ( 3) шага в обратную сторону, то окажешься в точке с координатой ( -3).
Какое расстояние было пройдено в первом и во втором случае?
Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки (( 3) и ( -3)), в которых ты оказался одинаково удалены от точки, из которой было начато движение (( 0)).
Таким образом, мы приблизились к понятию модуля.
Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.
Так, модулем числа ( 5) будет ( 5). Модуль числа ( -5) также равен ( 5).
Потому что расстояние не может быть отрицательным! Модуль – это абсолютная величина.
Обозначается модуль просто:
Итак, найдём модуль числа ( 3) и ( -3):
( left| mathbf right|=mathbf)
Основные свойства модуля
Первое свойство модуля
Если ( a) – отрицательное число, то его модуль равен противоположному числу.
А если ( a=0)? Ну, конечно! Его модуль также равен ( 0):
Из этого следует, что модули противоположных чисел равны, то есть:
( left| -4 right|text=textleft| 4 right|text=text4;)
( left| -7 right|text=textleft| 7 right|text=text7.)
А теперь потренируйся:
- ( left| 9 right|text=text?;)
- ( left| -3 right|text=text?;)
- ( left| 16 right|text=text?;)
- ( left| 8 right|text=text?;)
- ( left| -17 right|text=text?.)
Ответы: 9; 3; 16; 8; 17.
Довольно легко, правда? А если перед тобой вот такое число: ( left| 2-sqrt right|=?)
Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.
Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль:
- если значение выражения больше нуля, то просто выносим его из-под знака модуля,
- если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.
Ну что, попробуем? Оценим ( 2-sqrt):
( 2<sqrt) (Забыл, что такое корень? Бегом повторять!)
Если ( 2<sqrt), то какой знак имеет ( 2-sqrt)? Ну конечно, ( 2-sqrt<0)!
А, значит, знак модуля раскрываем, меняя знак у выражения:
( left| 2-sqrt right|=-left( 2-sqrt right)=-2+sqrt=sqrt-2)
Разобрался? Тогда попробуй сам:
- ( left| sqrt-1 right|=?)
- ( left| 3-sqrt right|=?)
- ( left| 2-sqrt right|=?)
- ( left| sqrt-4 right|=?)
Ответы:
Какими же ещё свойствами обладает модуль?
Во-первых, если нам нужно перемножить числа внутри знака модуля, мы спокойно можем перемножить модули этих чисел.
То есть: ( |acdot bleft| text=text right|aleft| cdot right|b|)
Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.
( left| mathbfcdot mathbf right|text=textleft| mathbf right|cdot left| mathbf right|text=textmathbfcdot mathbftext=textmathbf;)
( left| mathbfcdot left( -mathbf right) right|text=textleft| mathbf right|cdot left| -mathbf right|text=textmathbfcdot mathbftext=textmathbf.)
А что, если нам нужно разделить два числа (выражения) под знаком модуля? Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:
Еще одно свойство модуля…
Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел.
( |a+bleft| textle text right|aleft| + right|b|)
Почему так? Всё очень просто! Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное.
Допустим, что числа ( a) и ( b) оба положительные. Тогда левое выражение будет равно правому выражению. Рассмотрим на примере:
| ( left| mathbf+mathbf right|text=textleft| mathbf right|text=textmathbf) | ( left| mathbf right|+left| mathbf right|text=textmathbf+mathbftext=textmathbf) |
Выражения также равны, если оба числа отрицательны:
Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:
| ( left| -mathbf+mathbf right|text=textleft| mathbf right|text=textmathbf) | ( |-mathbfleft| + right|mathbf|text=textmathbf+mathbftext=textmathbf) |
| ( left| mathbf+left( -mathbf right) right|text=textleft| -mathbf right|text=textmathbf) | ( left| mathbf right|+left| -mathbf right|text=textmathbf+mathbftext=textmathbf) |
( mathbf<mathbf)
Рассмотрим еще парочку полезных свойств модуля
Что если перед нами такое выражение:
( left| 7x right|)
Что мы можем сделать с этим выражением?
Значение x нам неизвестно, но зато мы уже знаем, что ( |acdot bleft| text=text right|aleft| cdot right|b|), а значит ( left| 7x right|=left| 7 right|cdot left| x right|). Число ( 7) больше нуля, а значит можно просто записать:
( left| 7x right|=left| 7 right|cdot left| x right|=7left| x right|)
Вот мы и пришли к другому свойству, которое в общем виде можно представить так:
( left| cx right|=ccdot left| x right|,) при ( c>0)
А чему равно такое выражение:
Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?
Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему степень и ее свойства.
И что же получается? А вот что:
Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:
Ну, и почему сомнения? Действуем смело!
Во всем разобрался? Тогда вперед тренироваться на примерах!
Тренировка на примерах
1. Найдите значение выражения ( |xleft| text+text right|y|), если ( x=text-7,5text,y=text12.)
2. У каких чисел модуль равен ( 5)?
3. Найдите значение выражений:
в) ( |15left| cdot right|-3|;)
Если не все пока ясно и есть затруднения в решениях, то давай разбираться:
Решение 1:
Итак, подставим значения ( x) и ( y) в выражение ( |mathbfleft| text-text right|mathbf|.) Получим:
Решение 2:
Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное ( 5) имеют два числа: ( 5) и ( -5).
Решение 3:
Все уловил? Тогда пора перейти к более сложному!
Решение более сложных примеров
Попробуем упростить выражение ( left| sqrt-2 right|+left| sqrt+5 right|)
Решение:
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.
Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
( displaystyle sqrt approx 1,7). Получается, значение первого выражения под модулем ( displaystyle sqrt-2approx 1,7-2approx -0,3text).
( -0,3<0), следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:
Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Модуль числа и его свойства (строгие определения и доказательства)
Модуль (абсолютная величина) числа ( x) — это само число ( x), если ( xge 0), и число ( -x), если ( x<0):
Например: ( left| 4 right|=4;textleft| 0 right|=0;textleft| -3 right|=-left( -3 right)=3.)
Пример:
Упростите выражение ( left| sqrt-3 right|+left| sqrt+1 right|).
Решение:
( sqrt-3<0Rightarrow left| sqrt-3 right|=-left( sqrt-3 right)=3-sqrt;)
( sqrt+1>0Rightarrow left| sqrt+1 right|=sqrt+1;)
( left| sqrt-3 right|+left| sqrt+1 right|=3-sqrt+sqrt+1=4.)
Основные свойства модуля (итог)
Для всех ( x,yin mathbb):
- ( left| x right|ge 0,textleft| x right|=0Leftrightarrow x=0;)
- ( left| -x right|=left| x right|;)
- ( left| xcdot y right|=left| x right|cdot left| y right|;)
- ( left| fracright|=frac,textne text;)
- ( left| x+y right|le left| x right|+left| y right|)
- ( left| cx right|=ccdot left| x right|, при textc>0)
- ( ^>=^>)
Докажите свойство модуля: ( left| x+y right|le left| x right|+left| y right|)
Доказательство:
Предположим, что существуют такие ( x;yin mathbb), что ( left| x+y right|>left| x right|+left| y right|.) Возведем левую и правую части неравенства в квадрат (это можно сделать, т.к. обе части неравенства всегда неотрицательны):
( displaystyle beginleft| x+y right|>left| x right|+left| y right|Leftrightarrow \^>>^>Leftrightarrow \^>+2xy+^>>^>+2cdot left| x right|cdot left| y right|+^>Leftrightarrow \xy>left| x right|cdot left| y right|Leftrightarrow \xy>left| xy right|,end)
а это противоречит определению модуля.
Следовательно, таких ( x;yin mathbb) не существует, а значит, при всех ( x,textyin mathbb) выполняется неравенство ( left| x+y right|le left| x right|+left| y right|.)
А теперь самостоятельно…
Докажите свойство модуля: ( left| cx right|=ccdot left| x right|, при textc>0)
Воспользуемся свойством №3: ( left| ccdot x right|=left| c right|cdot left| x right|), а поскольку ( c>0textRightarrow textleft| c right|=c), тогда
( left| cx right|=ccdot left| x right|), ч.т.д.
Упростите выражение ( left| frac-sqrt right|+left| frac-sqrt right|)
Чтобы упростить, нужно раскрыть модули. А чтобы раскрыть модули, нужно узнать, положительны или отрицательны выражения под модулем:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
Наши курсы по подготовке к ЕГЭ по математике, информатике и физике
Марафон «ЕГЭ — год за месяц»
Весь май каждый день, кроме выходных
Алексей Шевчук — ведущий курсов
Твой ход!
Теперь ты знаешь все о модуле! Я уверен, что ты справишься с любой задачей! И я очень горжусь тобой.
Это было не так сложно, правда? Особенно, когда разбираешь все подробно и поэтапно.
А сейчас мы хотим услышать тебя! Как тебе статья? Понравился разбор понятия модуля?
Напиши в комментариях свое мнение об этой статье!
Мы читаем все. И ответим на любые твои вопросы.
Добавить комментарий Отменить ответ
11 комментариев
Лилия :
Здравствуйте, ещё раз. Пока писала Вам отзыв вставки с предложением зарегистрироваться исчезли. И теперь я могу прочитать статью полностью! Вот Спасибо!
С уважением Лилия.
Александр Кель :
Ну вот и славно! )
Лилия :
Здравствуйте, Александр.
Изумительная статья! Восхитительная! ВСЁ очень-очень доходчиво и понятно.
Большое спасибо за неё.
Но, изучая её, я наткнулась на вставочки, которые прерывают рассуждения автора. В этих вставках предлагается зарегистрироваться. Я это сделала.
Попав на страницы учебника, я не нашла этой статьи о модулях. И вообще не нашла ничего про модули.
Подскажите, пожалуйста, возможно ли так изменить статью, чтобы в ней не было вставок, а был текст полностью?
С огромным уважением к автору статьи Лилия
Александр Кель :
Спасибо, Лилия!
В другом комментарии я вижу, что вы уже разобрались, но просто на будущее, вот здесь содержание всего учебника: https://youclever.org/book/
По нему можно найти любую тему по подготовке к ОГЭ и ЕГЭ по математике.
Ольга Карасева :
Спасибо! Все очень доходчиво
Александр Кель :
И вам спасибо! Заходите ещё)
Матвеева Ксения :
Спасибо, я 7 -ой класс, как-то модуль в школе прошел тихо, незаметно, а сейчас столкнулась и поняла, что «0». Проработав Вашу статью все стало в голове на место.
Александр Кель :
Ксения — ты супер! Самостоятельно разобраться с модулем дорогого стоит. Приходи в ЭТО воскресенье 26 сентября на бесплатный вебинар, где Алексей будет разбирать как решать уравнения с модулем. Он для ЕГЭшников, но раз ты сама модуль разобрала, справишься и будешь по модулям совсем крутышка. ) Вот ссылка на доступ к вебинару: https://app.livewebinar.com/991-815-000
Pretty :
Спасибо большое, сидела психовала из за этой темы. А сейчас всё понятно.
Александр Кель :
Спасибо, Pretty. Заходи еще, мы сейчас улучшаем каждую статью — будет еще понятнее )
Александр Кель :
Некоторые комментарии прошлых лет к этой статье:
Виктория
27 мая 2018
Спасибо!
Александр (админ)
27 мая 2018
Пожалуйста, Виктория!
Мария
13 ноября 2018
огромное спасибо, многое вспомнила
Александр (админ)
13 ноября 2018
Пожалуйста, Мария!
Денис
17 февраля 2019
Спасибо большое за эту статью, многое вспомнил))
Александр (админ)
17 февраля 2019
Денис! Рады слышать! И тебе спасибо! )
Анастасия
13 мая 2019
Спасибо большое! Очень понятно рассмотрен материал!
Александр (админ)
13 мая 2019
Пожалуйста, Анастасия! Удачи на экзаменах!
Иван
25 мая 2019
В самом начале рассматриваются не все случаи выражения ∣√5 — 3∣ + ∣√5 + 1∣. Пропущен случай, когда √5 < 0, в этом случае выражение будет иметь вид 2√5 — 2 или 2(√5 — 1), а не 4.
Алексей Шевчук
29 мая 2019
Иван, √5 не может быть меньше нуля, это ведь вполне конкретное число (равное приблизительно 2,24, поэтому мы и пишем, что √5 — 30). И вообще, квадратный корень по определению не может быть отрицательным, какое бы число под ним не стояло.
МАРИЯ
31 июля 2019
Огромное спасибо, очень помогло!
Александр (админ)
31 июля 2019
Приятно слышать, Мария! Успехов!
Анастасия
15 февраля 2020
Большое спасибо! Все просто и понятно. Я вообще учусь в 6 классе и впервые сталкиваюсь с таким понятием как модуль. Ни учебник по математике, ни учитель не мог мне понятно объяснить! Я зашла сюда и удивилась : -это же легко!! Большое спасибо администратору.
Александр (админ)
15 февраля 2020
О, как круто! Спасибо, Анастасия. Ты молодец, что сама разобралась в такой теме. Хоть и с помощью нашего учебника, но все равно молодец! Так держать!
Модуль числа знак, свойства, действия, как найти, примеры графиков
Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.
Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам.
Что такое модуль в математике
Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.
Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.
Свойства модуля
Важно помнить о следующих свойствах:
- Правило раскрытия: абсолютная величина любого числа больше или равна нулю:
- Если абсолютные значения содержат выражения противоположных значений, они равны:
- Значение числа не превышает величину его модуля:
- Правило раскрытия при произведении:
- Правило, применимое при делении:
- При возведении в степень:
- Сумма величин:
- Двойной модуль:
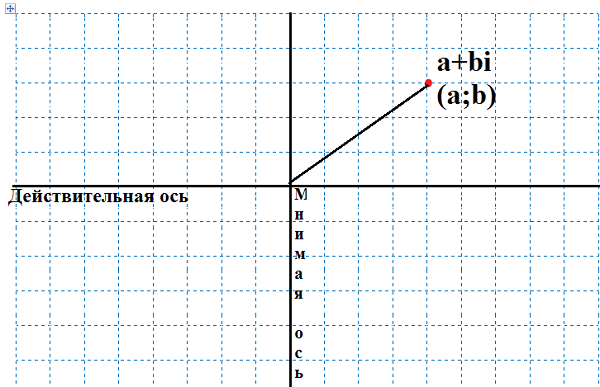
Модуль комплексного числа
Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).
Этот направленный отрезок также является вектором, представляющим комплексное число a + bi, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi.
Как решать уравнения с модулем
Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.
Уравнения типа |x| = a
Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.
Равенство с абсолютной величиной не имеет решения, если величина отрицательная.
Если |x| <, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.
Уравнения типа |x| = |y|
Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.
Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).
Далее простая арифметика − нужно решить два равенства относительно x.
Уравнения типа |x| = y
Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.
Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:
Решение неравенств с модулем
Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.
Уравнения вида |x| = a
Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.
Решение.
Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.
После перемещения константы вправо получено: |x| = 2.
Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.
Ответ: 2 и −2.
Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.
Решение.
Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.
Это означает, что –2 – поворотная точка.
Далее определяется знак на интервалах: на промежутке величина будет отрицательной, а на интервале будет положительной.
Разделим интервал на 2 части:
- для x + 2 ≥ 0
Общим ответом для этих двух неравенств является интервал [−1, + ∞).
- для х + 2 <, 0
Общим ответом для этих двух неравенств является интервал (−∞, –3].
Окончательное решение – объединение ответов отдельных частей:
Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).
Уравнения вида |x| = |y|
Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.
Решение:
Ответ: x1 = 3, x2 = − 1.
Пример 2 (алгебра 8 класс). Решить неравенство:
Решение:
Уравнения вида |x| = y
Пример 1 (алгебра 10 класс). Найти x:
Решение:
Очень важно провести проверку правой части, иначе можно написать в ответ ошибочные корни. Из системы видно, что не лежит в промежутке .
Ответ: x = 0.
Модуль суммы
Модуль разности
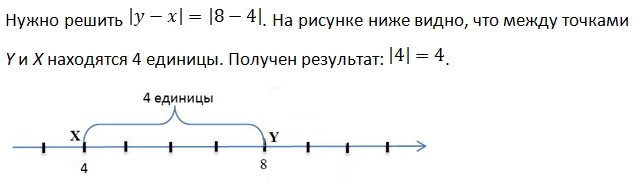
Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.
Пример 1.
Пример 2.
Модуль отрицательного числа
Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,
Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.
Модуль нуля
Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.
Модуль в квадрате
Модуль в квадрате всегда равен выражению в квадрате:
Примеры графиков с модулем
Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.
Пример 1.
Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.
Решение:
Объяснение: из рисунка видно, что график симметричен относительно оси Y.
Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.
Решение:
Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).
Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.
Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.
Метод интервалов в задачах с модулем
Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.
Для использования метода нужно совершить следующие действия:
- Приравнять каждое выражение к нулю.
- Найти значения переменных.
- Нанести на числовую прямую точки, полученные в пункте 2.
- Определить на промежутках знак выражений (отрицательное или положительное значение) и нарисовать символ – или + соответственно. Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка).
- Решить неравенства с полученными знаками.
Пример 1. Решить методом интервалов.
Решение:
Результатом будет сумма всех подходящих интервалов.
Модуль в модуле
Среди примеров часто встречаются уравнения, где нужно найти корни равенств такого вида: ||ax – b| – c| = kx + m.
Лучше всего понять принцип на примере.
Пример 1. Решить
Решение:
Первым делом нужно раскрыть внутренний модуль. Для этого рассматривается два варианта:
В первом случае выражение положительное, а во втором отрицательное. Исходя из этого, получаем:
Нужно упростить два уравнения:
Далее каждое из равенств разделяется еще на два:
Получено четыре результата:
Заключение
Самое важное, что нужно знать: модуль не может быть отрицательным.
Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.
В качестве итогов, напомним все свойства, которые помогут в решении задач:
- когда положительное число находится внутри модуля, достаточно просто избавиться от него,
- если есть выражение, нужно его упростить, прежде чем найти абсолютное значение,
- если равенство содержит две переменные, нужно решать его с помощью системы уравнений и за основу брать методы решения выражений с абсолютными величинами.
Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.
Как найти число по модулю?
- Знак модуля: |a| = OA.
- Модуль числа — это расстояние, а расстояние не может быть отрицательным. …
- Модуль положительного числа равен самому числу.
- Модуль отрицательного числа равен противоположному числу.
- Модуль нуля равен нулю.
- Противоположные числа имеют равные модули.
Как решить модуль числа?
1:105:30Рекомендуемый клип · 55 сек.Модуль числа. Математика 6 класс. — YouTubeYouTubeНачало рекомендуемого клипаКонец рекомендуемого клипа
В каком случае модуль отрицательный?
Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу. Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Как делить числа по модулю?
На практике считается, что делить можно только в поле по простому модулю. Деление по модулю определяется через умножение следующим образом: abmodb=(a∗1b)modm=ab−1modm. Ключевую роль играет значение b−1, называющееся обратный элемент в поле по модулю.
Как называется целое число?
Це́лые чи́сла — расширение множества натуральных чисел, получаемое добавлением к нему нуля и отрицательных чисел. Необходимость рассмотрения целых чисел продиктована невозможностью в общем случае вычесть из одного натурального числа другое — можно вычитать только меньшее число из большего.
Какие числа имеют одинаковый модуль?
Противоположные числа имеют одинаковый модуль.
Как правильно сложить модуль?
Чтобы сложить положительное и отрицательное число, нужно:
- Найти модули слагаемых — то есть этих чисел.
- Сравнить полученные числа. …
- Из большего модуля вычесть меньший.
- Перед полученным числом поставить знак того слагаемого, модуль которого больше.
29 дек. 2020 г.
Как найти модуль положительного числа или 0?
Модуль положительного числа равен самому числу. Модуль отрицательного числа равен противоположному числу. Модуль нуля равен нулю.
Можно ли вынести минус из модуля?
Модулем рационального числа называют расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу. Так как расстояние (длина отрезка) может выражаться только положительным числом или нулём, можно сказать, что модуль числа не может быть отрицательным.
Когда можно убрать знак модуля?
1) Модуль всегда равен положительному числу. 2) Если под знаком модуля положительное число, то знак модуля просто снимается. 3) Если под знаком модуля отрицательное число, то у него меняется знак на противоположный, и оно становится положительным.
Что такое деление по модулю?
Деление по модулю — арифметическая операция, результатом которой является остаток от деления целого числа на другое целое число.
Как поделить без остатка в Питоне?
Деление без остатка Чтобы выполнить деление на цело в Python, можно воспользоваться целочисленным делением. В этом случае результатом будет целое число, без остатка. Целочисленное деление в Python обозначается двумя косыми чертами «//».
Какие числа называются целыми пример?
Что такое целое число — это натуральное число, а также противоположное ему число и нуль. Примеры целых чисел: -7, 222, 0, 569321, -12345 и др. Что важно знать о целых числах: Сумма, разность и произведение целых чисел в результате дают целые числа.
Какие числа называют Неположительными?
Неположительные числа — это все отрицательные числа и число 0. Пример: выбери из чисел: -45; 10,1; -1,2; 0; 8,6; -0,0759; 4028 — неположительные числа.
Что такое модуль приведите примеры?
Модуль числа – это расстояние от нуля до данного числа. Например, |-5| = 5. То есть расстояние от точки -5 до нуля равно 5.
Как сложить два модуля?
Чтобы сложить числа с разными знаками:
- из большего модуля вычесть меньший модуль;
- в результате поставить знак слагаемого с большим модулем.
29 дек. 2020 г.
Что такое модуль в программе?
Модуль (программирование) — функционально законченный фрагмент программы, оформленный в виде отдельного файла с исходным кодом или поименованной непрерывной её части. Исполнимый модуль — файл, содержащий программу в виде, в котором она может быть исполнена компьютером.
Модуль числа — теория и решение задач
Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности 🙂
А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.
Вот смотри…
Ситуация первая
В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.
Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.
Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.
Ситуация вторая
Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.
И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?
Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.
Ситуация третья
В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.
А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.
Ну вот, ты уже почти все знаешь. Давай теперь подробнее…
Модуль числа — коротко о главном
Определение модуля:
Модуль (абсолютная величина) числа ( displaystyle x) — это само число ( displaystyle x), если ( displaystyle xge 0), и число ( displaystyle -x), если ( displaystyle x<0):
( displaystyle left| x right|=left{ begin{array}{l}x, xge 0\-x, x<0end{array} right.)
Свойства модуля:
- Модуль числа есть число неотрицательное: ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0);
- Модули противоположных чисел равны: ( left| -x right|=left| x right|);
- Модуль произведения двух (и более) чисел равен произведению их модулей: ( left| xcdot yright|=left| x right|cdot left|yright|);
- Модуль частного двух чисел равен частному их модулей: ( displaystyle left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0});
- Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:( left| x+y right|le left| x right|+left| y right|);
- Постоянный положительный множитель можно выносить за знак модуля: ( left| cx right|=ccdot left| x right|) при ( displaystyle c>0);
- Квадрат модуля числа равен квадрату этого числа: ( {{left| x right|}^{2}}={{x}^{2}}).
Кстати, в продолжение этой темы у нас есть отличная статья: «Уравнения с модулем«. Когда прочитаешь эту статью, обязательно ознакомься и со второй.
И просто чтобы ты знал, модуль часто попадается при решении квадратных уравнений или иррациональных.
Что же такое модуль числа?
Представь, что это ты.
Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления ( 0).
Итак, ты делаешь ( 3) шага вперёд и оказываешься в точке с координатой ( 3).
Это означает, что ты удалился от места, где стоял на (3) шага (( 3) единичных отрезка).
То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно ( 3).
Но ведь ты же можешь двигаться и назад!
Если от отправной точки с координатой ( 0) сделать ( 3) шага в обратную сторону, то окажешься в точке с координатой ( -3).
Какое расстояние было пройдено в первом и во втором случае?
Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки (( 3) и ( -3)), в которых ты оказался одинаково удалены от точки, из которой было начато движение (( 0)).
Таким образом, мы приблизились к понятию модуля.
Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.
Так, модулем числа ( 5) будет ( 5). Модуль числа ( -5) также равен ( 5).
Потому что расстояние не может быть отрицательным! Модуль – это абсолютная величина.
Обозначается модуль просто:
( |mathbf{a}|,) (( a) — любое число).
Итак, найдём модуль числа ( 3) и ( -3):
( left| mathbf{3} right|=mathbf{3})
( left| -mathbf{3} right|=mathbf{3}.)
Основные свойства модуля
Первое свойство модуля
Модуль не может быть выражен отрицательным числом ( |mathbf{a}|text{ }ge text{ }mathbf{0})
То есть, если ( mathbf{a}) – число положительное, то его модуль будет равен этому же числу.
Если ( mathbf{a}text{ }>text{ }mathbf{0},) то ( displaystyle left| a right|=a).
Если ( a) – отрицательное число, то его модуль равен противоположному числу.
Если ( atext{ }<text{ }mathbf{0},) то ( |mathbf{a}|text{ }=text{ }-mathbf{a})
А если ( a=0)? Ну, конечно! Его модуль также равен ( 0):
Если ( a=0), то ( |mathbf{a}|=mathbf{a}), или ( displaystyle left| 0 right|=0).
Из этого следует, что модули противоположных чисел равны, то есть:
( left| -4 right|text{ }=text{ }left| 4 right|text{ }=text{ }4;)
( left| -7 right|text{ }=text{ }left| 7 right|text{ }=text{ }7.)
А теперь потренируйся:
- ( left| 9 right|text{ }=text{ }?;)
- ( left| -3 right|text{ }=text{ }?;)
- ( left| 16 right|text{ }=text{ }?;)
- ( left| 8 right|text{ }=text{ }?;)
- ( left| -17 right|text{ }=text{ }?.)
Ответы: 9; 3; 16; 8; 17.
Довольно легко, правда? А если перед тобой вот такое число: ( left| 2-sqrt{5} right|=?)
Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.
Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль:
- если значение выражения больше нуля, то просто выносим его из-под знака модуля,
- если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.
Ну что, попробуем? Оценим ( 2-sqrt{5}):
( 2<sqrt{5}) (Забыл, что такое корень? Бегом повторять!)
Если ( 2<sqrt{5}), то какой знак имеет ( 2-sqrt{5})? Ну конечно, ( 2-sqrt{5}<0)!
А, значит, знак модуля раскрываем, меняя знак у выражения:
( left| 2-sqrt{5} right|=-left( 2-sqrt{5} right)=-2+sqrt{5}=sqrt{5}-2)
Разобрался? Тогда попробуй сам:
- ( left| sqrt{3}-1 right|=?)
- ( left| 3-sqrt{7} right|=?)
- ( left| 2-sqrt{7} right|=?)
- ( left| sqrt{13}-4 right|=?)
Ответы:
( sqrt{3}-1; 3-sqrt{7}; sqrt{7}-2; 4-sqrt{13.})
Какими же ещё свойствами обладает модуль?
Во-первых, если нам нужно перемножить числа внутри знака модуля, мы спокойно можем перемножить модули этих чисел.
То есть: ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|)
Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.
Например:
( left| mathbf{5}cdot mathbf{7} right|text{ }=text{ }left| mathbf{5} right|cdot left| mathbf{7} right|text{ }=text{ }mathbf{5}cdot mathbf{7}text{ }=text{ }mathbf{35};)
( left| mathbf{3}cdot left( -mathbf{2} right) right|text{ }=text{ }left| mathbf{3} right|cdot left| -mathbf{2} right|text{ }=text{ }mathbf{3}cdot mathbf{2}text{ }=text{ }mathbf{6}.)
А что, если нам нужно разделить два числа (выражения) под знаком модуля? Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:
( displaystyle |frac{a}{b}|=frac{|a|}{|b|}) при условии, что ( mathbf{b}ne mathbf{0}) (так как на ноль делить нельзя).
Еще одно свойство модуля…
Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел.
( |a+bleft| text{ }le text{ } right|aleft| + right|b|)
Почему так? Всё очень просто! Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное.
Допустим, что числа ( a) и ( b) оба положительные. Тогда левое выражение будет равно правому выражению. Рассмотрим на примере:
| ( left| mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{10} right|text{ }=text{ }mathbf{10}) | ( left| mathbf{3} right|+left| mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
Выражения также равны, если оба числа отрицательны:
| ( displaystyle |-3+(-7)|~=~|-3-7|~)( displaystyle=|-10|=10) | ( |-mathbf{3}left| + right|-mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:
| ( left| -mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{4} right|text{ }=text{ }mathbf{4}) | ( |-mathbf{3}left| + right|mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
или
| ( left| mathbf{3}+left( -mathbf{7} right) right|text{ }=text{ }left| -mathbf{4} right|text{ }=text{ }mathbf{4}) | ( left| mathbf{3} right|+left| -mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
( mathbf{4}<mathbf{10})
Рассмотрим еще парочку полезных свойств модуля
Что если перед нами такое выражение:
( left| 7x right|)
Что мы можем сделать с этим выражением?
Значение x нам неизвестно, но зато мы уже знаем, что ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|), а значит ( left| 7x right|=left| 7 right|cdot left| x right|). Число ( 7) больше нуля, а значит можно просто записать:
( left| 7x right|=left| 7 right|cdot left| x right|=7left| x right|)
Вот мы и пришли к другому свойству, которое в общем виде можно представить так:
( left| cx right|=ccdot left| x right|,) при ( c>0)
А чему равно такое выражение:
( {{left| x right|}^{2}}=?)
Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?
Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему степень и ее свойства.
И что же получается? А вот что:
( {{left| x right|}^{2}}={{x}^{2}})
Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:
( {{left| 5 right|}^{2}}={{5}^{2}}=25)
( {{left| -5 right|}^{2}}=?)
Ну, и почему сомнения? Действуем смело!
( {{left| -5 right|}^{2}}={{5}^{2}}=25)
Во всем разобрался? Тогда вперед тренироваться на примерах!
Тренировка на примерах
1. Найдите значение выражения ( |xleft| text{ }+text{ } right|y|), если ( x=text{ }-7,5text{ },y=text{ }12.)
2. У каких чисел модуль равен ( 5)?
3. Найдите значение выражений:
а) ( |3|text{ }+text{ }|-9|;)
б) ( |-5|text{ }-text{ }|6|;)
в) ( |15left| cdot right|-3|;)
г) ( displaystyle frac{|8|}{|-2|}).
Если не все пока ясно и есть затруднения в решениях, то давай разбираться:
Решение 1:
Итак, подставим значения ( x) и ( y) в выражение ( |mathbf{x}left| text{ }-text{ } right|mathbf{y}|.) Получим:
( |-7,5|text{ }+text{ }|12|text{ }=7,5text{ }+text{ }12text{ }=text{ }19,5.)
Решение 2:
Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное ( 5) имеют два числа: ( 5) и ( -5).
Решение 3:
а) ( |3|text{ }+text{ }|-9|=text{ }3+9=text{ }12;)
б) ( |-5|-text{ }left| 6 right|text{ }=text{ }5-6=text{ }-1;)
в) ( |15left| cdot right|-3|text{ }=text{ }15cdot 3=text{ }45;)
г) ( frac{|8|}{|-2|}=frac{8}{2}=4.)
Все уловил? Тогда пора перейти к более сложному!
Решение более сложных примеров
Попробуем упростить выражение ( left| sqrt{3}-2 right|+left| sqrt{3}+5 right|)
Решение:
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.
Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
( displaystyle sqrt{3} approx 1,7). Получается, значение первого выражения под модулем ( displaystyle sqrt{3}-2approx 1,7-2approx -0,3text{ }).
( -0,3<0), следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:
Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:
Модуль числа и его свойства (строгие определения и доказательства)
Модуль (абсолютная величина) числа ( x) — это само число ( x), если ( xge 0), и число ( -x), если ( x<0):
( left| x right|=left{ begin{array}{l}x,text{ }xge 0\-x,text{ }x<0end{array} right.)
Например: ( left| 4 right|=4;text{ }left| 0 right|=0;text{ }left| -3 right|=-left( -3 right)=3.)
Пример:
Упростите выражение ( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|).
Решение:
( sqrt{5}-3<0Rightarrow left| sqrt{5}-3 right|=-left( sqrt{5}-3 right)=3-sqrt{5};)
( sqrt{5}+1>0Rightarrow left| sqrt{5}+1 right|=sqrt{5}+1;)
( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|=3-sqrt{5}+sqrt{5}+1=4.)
Основные свойства модуля (итог)
Для всех ( x,yin mathbb{R}):
- ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0;)
- ( left| -x right|=left| x right|;)
- ( left| xcdot y right|=left| x right|cdot left| y right|;)
- ( left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0};)
- ( left| x+y right|le left| x right|+left| y right|)
- ( left| cx right|=ccdot left| x right|, при text{ }c>0)
- ( {{left| x right|}^{2}}={{x}^{2}})
Докажите свойство модуля: ( left| x+y right|le left| x right|+left| y right|)
Доказательство:
Предположим, что существуют такие ( x;yin mathbb{R}), что ( left| x+y right|>left| x right|+left| y right|.) Возведем левую и правую части неравенства в квадрат (это можно сделать, т.к. обе части неравенства всегда неотрицательны):
( displaystyle begin{array}{l}left| x+y right|>left| x right|+left| y right|Leftrightarrow \{{left( x+y right)}^{2}}>{{left( left| x right|+left| y right| right)}^{2}}Leftrightarrow \{{x}^{2}}+2xy+{{y}^{2}}>{{x}^{2}}+2cdot left| x right|cdot left| y right|+{{y}^{2}}Leftrightarrow \xy>left| x right|cdot left| y right|Leftrightarrow \xy>left| xy right|,end{array})
а это противоречит определению модуля.
Следовательно, таких ( x;yin mathbb{R}) не существует, а значит, при всех ( x,text{ }yin mathbb{R}) выполняется неравенство ( left| x+y right|le left| x right|+left| y right|.)
А теперь самостоятельно…
Докажите свойство модуля: ( left| cx right|=ccdot left| x right|, при text{ }c>0)
Воспользуемся свойством №3: ( left| ccdot x right|=left| c right|cdot left| x right|), а поскольку ( c>0text{ }Rightarrow text{ }left| c right|=c), тогда
( left| cx right|=ccdot left| x right|), ч.т.д.
Упростите выражение ( left| frac{31}{8}-sqrt{15} right|+left| frac{15}{4}-sqrt{15} right|)
Чтобы упростить, нужно раскрыть модули. А чтобы раскрыть модули, нужно узнать, положительны или отрицательны выражения под модулем:
Подготовка к ЕГЭ на 90+ в мини-группах
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
На этой странице вы узнаете
- Как перевернуть график модуля?
- Одной ногой тут, другой там: к какому промежутку относить граничные точки?
- Может ли решением квадратного неравенства быть любое число, если дискриминант меньше 0?
Модуль числа — это великая математическая мудрость, которая показывает дружбу и соперничество противоположных знаков: минуса и плюса. О том, что держит число в рамках, узнаем в статье.
Модуль
Мы легко можем найти расстояние от точки до точки, достаточно просто измерить его линейкой. Но можно ли найти расстояние от 0 до любого числа?
Представим, что наш дом находится посередине между школой и магазином. И до школы, и до магазина 500 метров, но они стоят по разные стороны от дома.
Расположим их на координатной прямой. Поскольку и школа, и магазин располагаются на одинаковом расстоянии, то от дома до них мы будем идти 500 метров. Но на координатной прямой до школы мы пройдем −500 метров, поскольку движемся против направления оси, а до магазина 500 метров.

Будет ли являться полученный результат противоречием? Нет, поскольку когда мы ищем расстояние, нам неважно направление движения и знак. В математике существует специальное определение — это модуль, или абсолютная величина.
Модуль — расстояние от любой точки на координатной прямой до начала координат.
Поскольку на координатной прямой мы можем отложить расстояние в две стороны, то такое расстояние можно найти и с отрицательными точками, и с положительными. Расстояние измеряет длину отрезка, то есть оно всегда будет положительно.
Можно сказать, что от любого числа модуль берет только цифры, а на знаки не обращает внимания. Например, |−8| = 8 и |8| = 8.
Может возникнуть вопрос: куда исчезает минус? Чтобы избавиться от минуса, достаточно умножить число на −1: (-8) * (-1) = 8. Значит, модуль просто умножает число на -1.
Отсюда получается, что модулем числа а называют выражение:

Возьмем два случая: a = 8 и a = -8. Для первого получаем |8| = 8, а для второго |-8| = -(-8) = 8, то есть определение выполняется.
Можно ли взять модуль функции? Да. Модулем произвольной функции называют выражение:
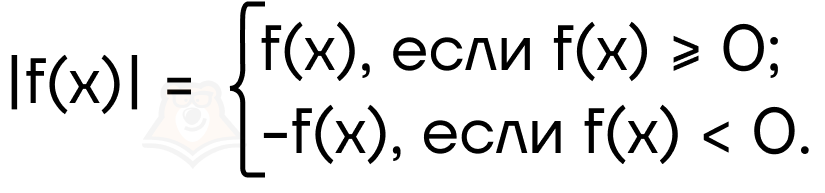
Свойства модуля
Модуль, как и все понятия в математике, обладает своими свойствами.
Свойство 1. |a| >= 0.
Как мы уже говорили, модуль всегда будет положительным числом, поскольку он не обращает внимания на знак числа.

Свойство 2. |a| = |-a|.
Это свойство также подтверждает рассуждения выше. Модули противоположных чисел, то есть чисел с разными знаками, равны.
Свойство 3. |a| >= a.
Если число а будет положительным, например, 5, то неравенство |5| >= 5 (rightarrow) 5 >= 5 выполняется, поскольку знак неравенства нестрогий.
Если число а будет отрицательным, например, -5, то неравенство |-5| >= -5 (rightarrow) 5 >= -5 выполняется, поскольку положительное число всегда больше отрицательного.
Свойство 4. |a * b| = |a| * |b|.
Пусть a = 5, b = -2, тогда |5 * (-2) | = |-10| = 10, и |5| * |-2| = 5 * 2 = 10, то есть выражения равны между собой.
Свойство 5. (|frac{a}{b}| = frac{|a|}{|b|}).
Рассуждения такие же, как и в предыдущем свойстве. Пусть a = 10, b = -5, тогда (|frac{10}{(-5)}| = |-2| = 2 и frac{|10|}{|-5|} = frac{10}{5} = 2).
Свойство 6. |a + b| <= |a| + |b|.
Почему появилось неравенство, а не уравнение, как в предыдущих двух свойствах? Разберем два примера.
Пусть a = 1, b = 2, тогда |1 + 2| = |3| = 3 и |1| + |2| = 1 + 2 = 3 — неравенство выполняется, поскольку знак нестрогий.
Но если a = -1, b = 2, тогда |-1 +2| = |1| = 1 и |-1| + |2| = 1 + 2 = 3, откуда получаем 1 < 3.
Свойство 7. (sqrt{a^2} = |a|).
Докажем это свойство. Пусть (sqrt{a^2} = x), тогда x0, поскольку квадратный «Корень» не может быть отрицательным. Возведем полученное уравнение в квадрат: a2 = x2
a2 — x2 = 0
(a — x)(a + x) = 0
Из уравнения x = a, из-за ограничений на x получаем a >= 0.
И x = -a, из-за ограничений на x получаем a < 0.
То есть получается выражение модуля.
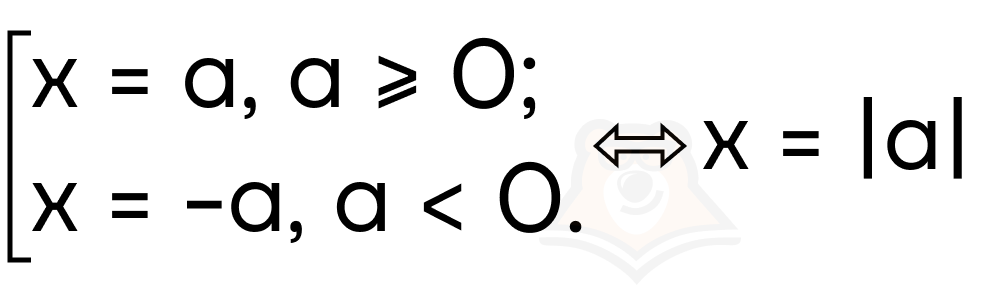
Свойство 8. |a|2 = a2.
Поскольку и модуль, и квадрат числа дают положительный результат, модуль в квадрате можно заменить просто квадратом числа.
График модуля
Как изобразить функцию с модулем? Для начала разберемся, что делает модуль с графиком функции.
Рассмотрим функцию y = x — это прямая. При этом у может быть и положительным, и отрицательным.
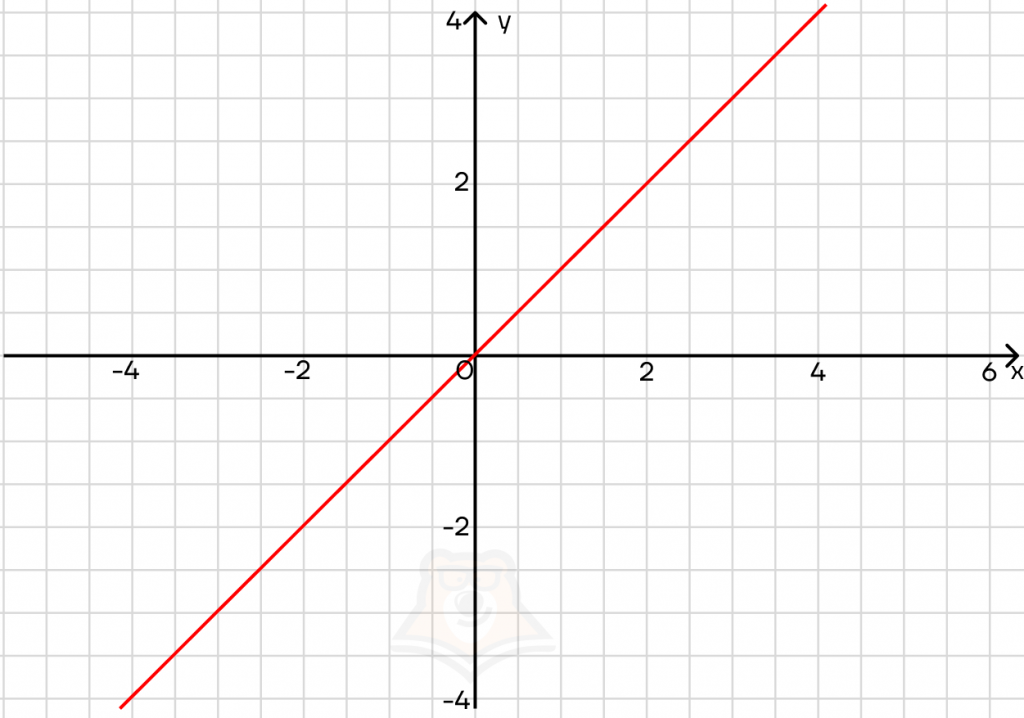
Занесем х под знак модуля: y = |x|. Теперь у может быть только положительным. Что происходит с частью графика, которая лежит ниже оси х? Она зеркально отражается. В итоге мы получаем галочку:
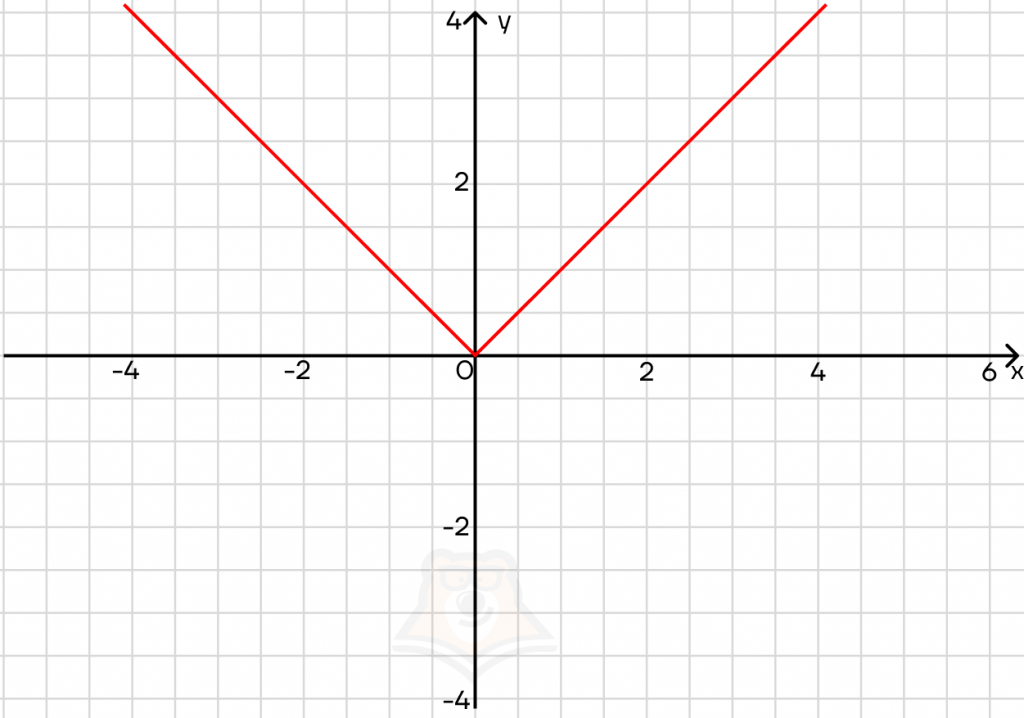
Модуль отражает любой график относительно оси х.
Что будет, если перед х будет стоять коэффициент? Построим графики:
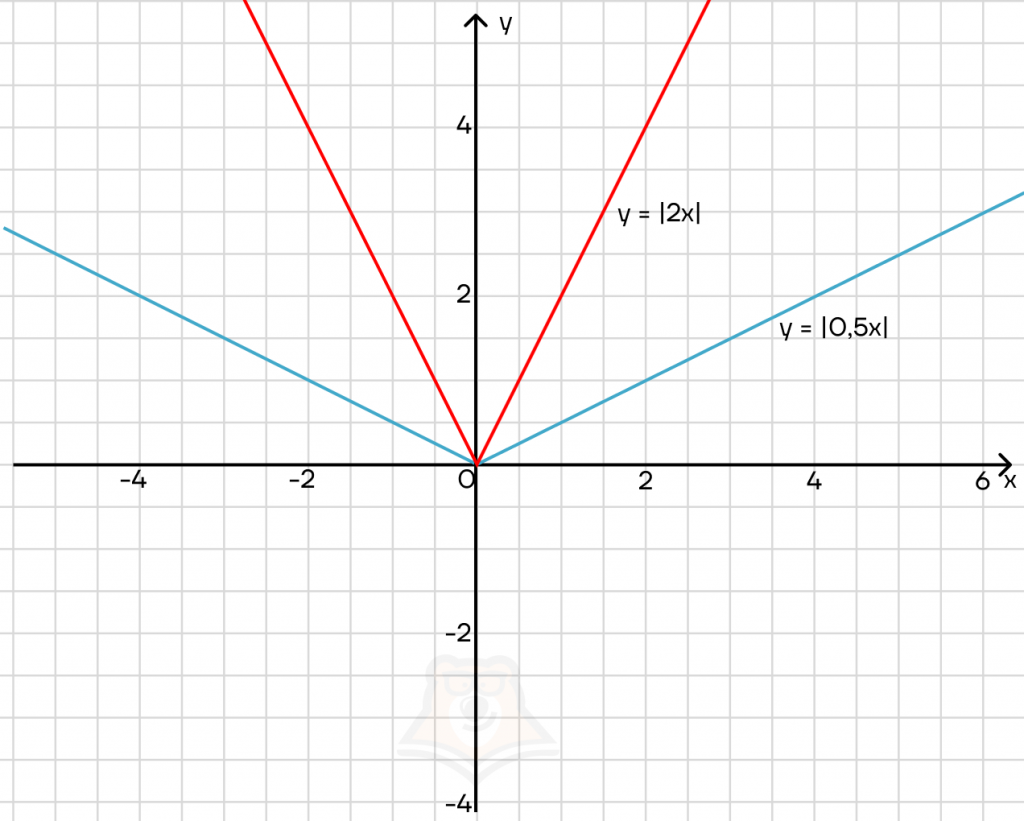
Галочка будет сужаться и расширяться. Причем чем больше коэффициент перед х, тем ýже будет галочка.
Попробуем добавить слагаемое к подмодульному выражению.
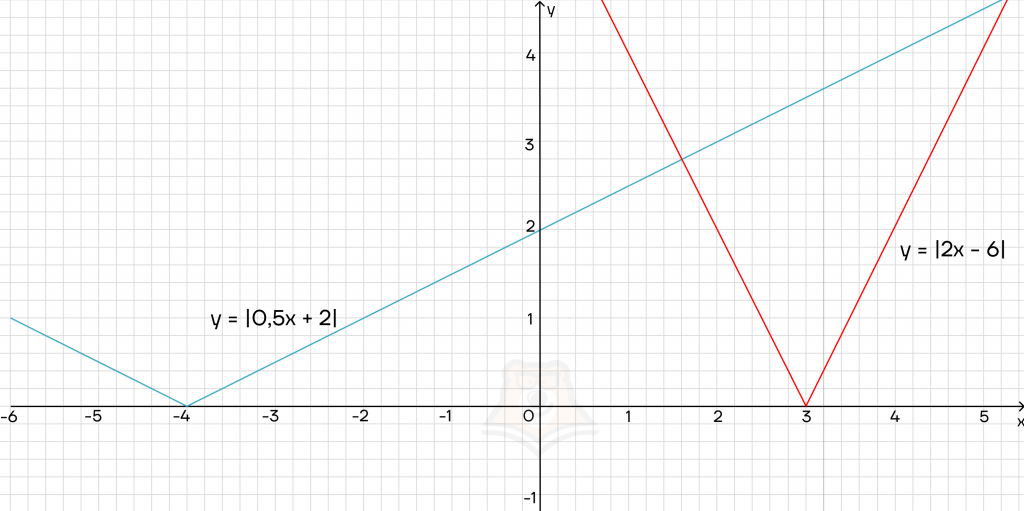
График модуля будет двигаться вдоль оси х. Причем:
- если мы прибавляем число, то график сдвигается влево;
- если мы вычитаем число, то график сдвигается вправо.
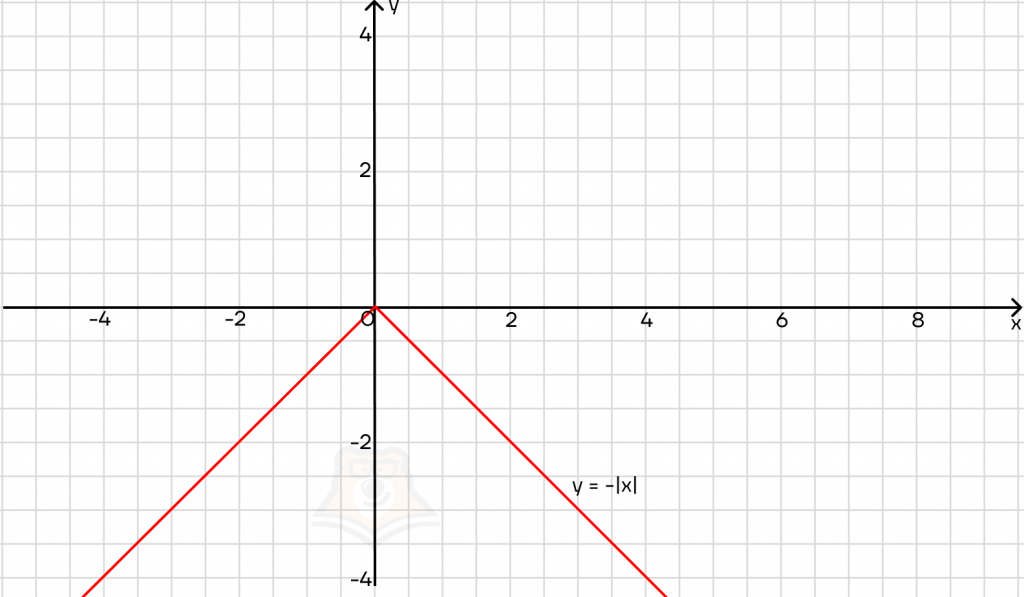
Добавим число к модулю, а не подмодульному выражению:
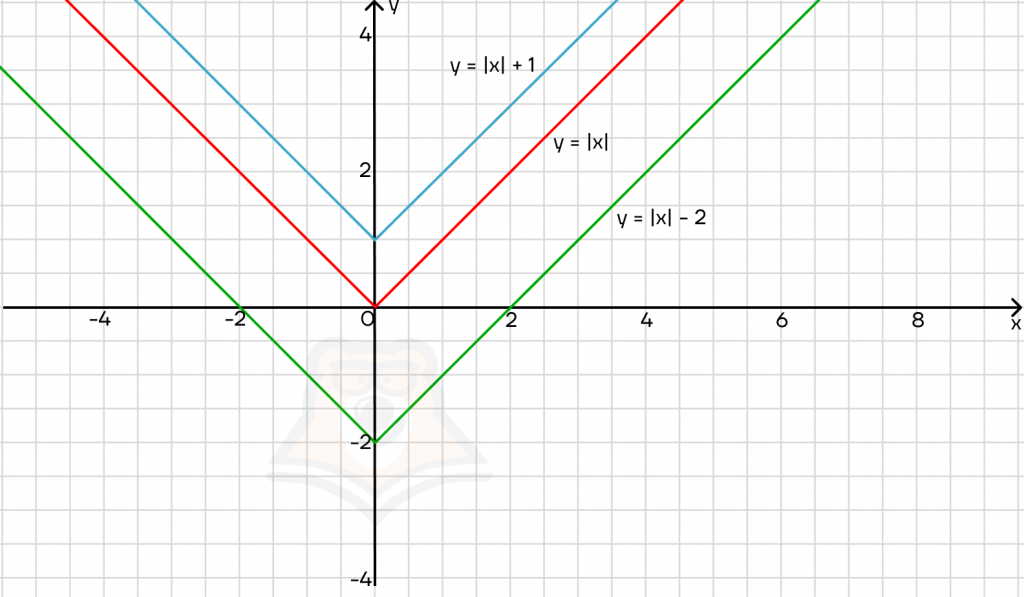
График будет двигаться вдоль оси у.
Для этого достаточно добавить перед модулем минус. Важно, чтобы минус стоял именно перед модулем, а не внутри него. Тогда график будет отзеркален относительно оси х и лежать только ниже нее.
Это легко проследить с помощью уравнений: если y = -|x|, то, при x = 3 получаем:
y = -|3| = -3
Уравнения с модулем
1. Возьмем уравнение вида |f(x)| = a. Поскольку модуль не может быть отрицательным, то и а не может быть отрицательным. Получаем следующий переход:
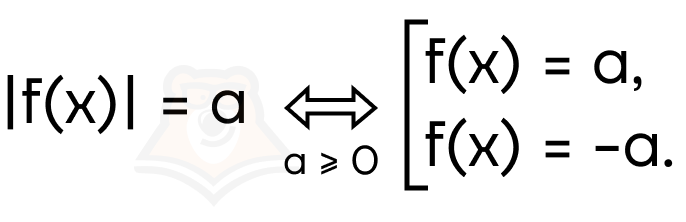
Пример 1. Решите уравнение |4x + 5| = 7.
Решение. В уравнении f(x) = 4x + 5, a = 7. Воспользуемся переходом:
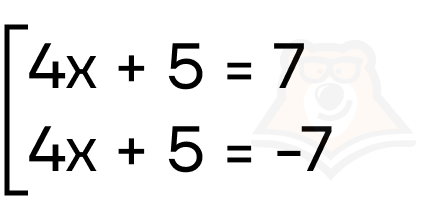
Из первого уравнения x = 0,5, а из второго уравнения x = -3.
Ответ: 0,5: -3.
2. В уравнениях и неравенствах можно встретить два разных модуля. Как быть в этом случае?
Шаг 1. Находим нули подмодульных выражений.
Шаг 2. Чертим числовую прямую и ищем знаки на промежутках для каждого модуля. Если подмодульное выражение отрицательно на промежутке, то ставится минус, если положительно — ставится плюс.
Шаг 3. Для каждого промежутка раскрываем модули. Если подмодульное выражение на промежутке отрицательно, то модуль раскрывается со знаком минус. Если положительно — модуль раскрывается со знаком плюс. Важно: полученные корни должны принадлежать промежуткам, на которых раскрывается модуль, иначе они не будут решениями уравнения.
Шаг 4. Записать все полученные корни в ответ.
Пример 2. Решите уравнение |x — 2| — |x + 2| = 4x — 5.
Решение. Найдем, в каких точках модули будут равны 0. Для этого подмодульное выражение также должно быть равно 0:
x — 2 = 0 (rightarrow) x = 2
x + 2 = 0 (rightarrow) x = -2
Нарисуем числовую прямую с этими точками:
У нас получилось три промежутка:
- (-(infty);-2)
- [-2;2)
- [2;+(infty))
Обратим внимание, какие знаки имеет первый модуль на промежутках: x — 2 > 0 при x > 2. Следовательно, на первых двух промежутках модуль будет отрицательным, а на третьем положительным. Расставим его знаки красным цветом.
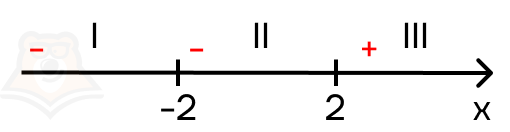
Проанализируем второй модуль: x + 2 > 0 (rightarrow) x>-2. Получается, подмодульное выражение будет положительно на втором и третьем промежутке, и отрицательным на первом промежутке. Расставим его знаки синим цветом.
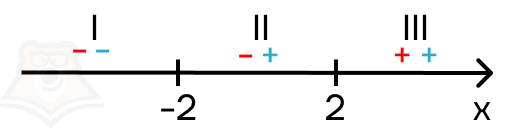
Теперь мы можем рассмотреть уравнение на всех трех промежутках. Однако для этого обязательно ввести ограничения: полученные точки должны принадлежать только этому промежутку, поскольку на следующем модули будут раскрываться уже по-другому.
2. Рассмотрим первый промежуток: x<-2. Оба модуля раскрываются с отрицательным знаком, и мы получаем следующее уравнение:
-(x — 2) — (-(x + 2)) = 4x — 5
-x + 2 + x + 2 = 4x — 5
4 = 4x — 5
4x = 9
x = 2,25
Точка не удовлетворяет ограничению, поскольку не лежит в промежутке (-(infty);-2):
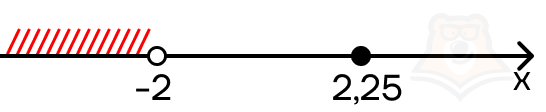
Рассмотрим второй промежуток: [-2;2). Первый модуль раскрывается с минусом, а второй с плюсом:
-(x — 2) — (x + 2) = 4x — 5
-x + 2 — x — 2 = 4x — 5
-2x = 4x — 5
6x = 5
(x = frac{5}{6})
Эта точка лежит в заданном промежутке и является решением уравнения.
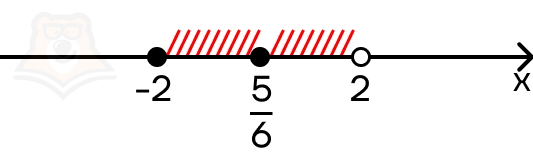
Рассмотрим третий промежуток [2;+(infty)). Оба модуля раскрываются со знаком плюс, мы получаем уравнение:
(x — 2) — (x + 2) = 4x — 5
x — 2 — x — 2 = 4x — 5
-4 = 4x — 5
4x = 1
x = 0,25 — эта точка не лежит в промежутке, то есть не является решением уравнения.
Решением уравнения будет только (x = frac{5}{6}).
Ответ: (frac{5}{6})
Разбивая прямую на промежутки, может возникнуть вопрос: а что делать с точками, в которых модуль равен 0? Их обязательно нужно проверять. Можно сделать это как отдельно, подставив точки в уравнение, так и сразу включить их в условие раскрытия модуля.
Если точки включаются в условие раскрытия модуля, то достаточно включить их только в один из двух промежутков. Включать их в два промежутка нецелесообразно: одна и та же точка будет проверяться дважды.

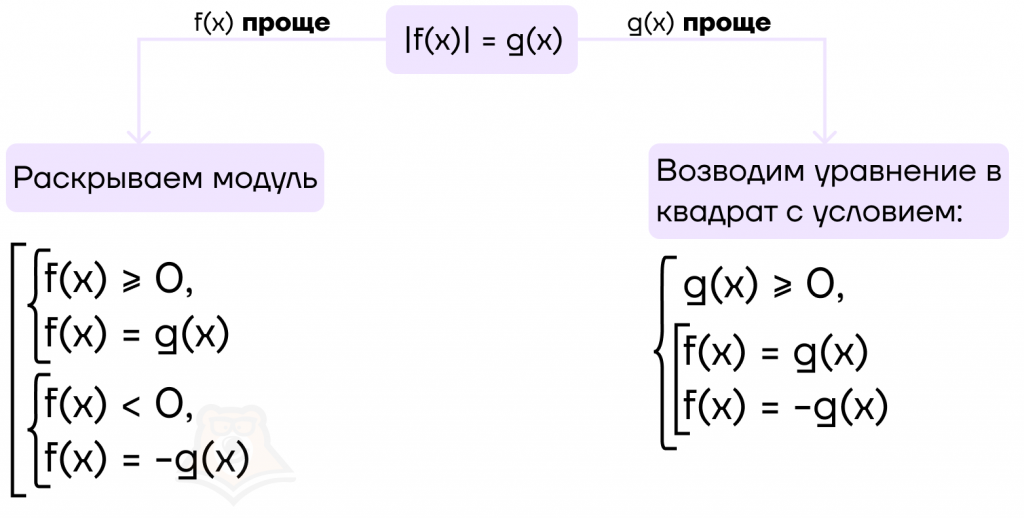
3. Уравнения вида |f(x)| = g(x)
Поскольку вместо функций могут стоять любые выражения, раскрыть модуль можно двумя способами. Выбор одного из них зависит от того, какая функция проще: f(x) или g(x).
Как можно раскрыть модуль?
- Можно раскрыть его в зависимости от знаков подмодульного выражения: если подмодульное выражение отрицательное, то модуль раскрывается с минусом, если положительное, то с плюсом.
- Можно возвести уравнение в квадрат. Но здесь необходимо ввести ограничения на g(x) — поскольку функция равна модулю, она не может быть отрицательной.
Для удобства можно пользоваться следующей схемой:
Пример 3. Решите уравнение |8 — x| = x2 — 5x + 11.
Решение. Заметим, что подмодульное выражение значительно проще функции справа, в этом случае удобнее будет раскрыть модуль. Получаем совокупность двух систем:
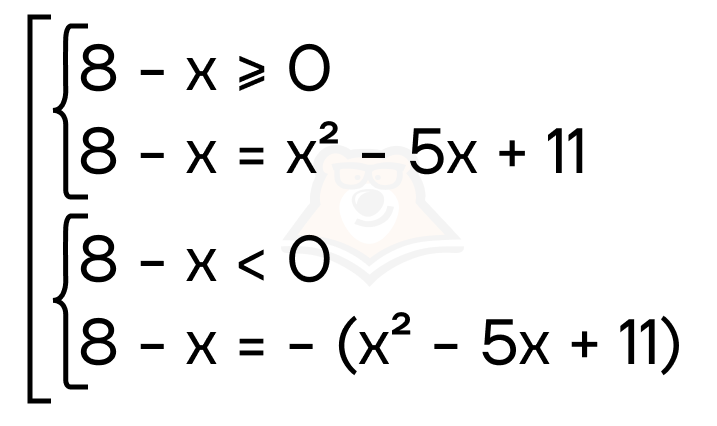
Рассмотрим первую систему.
8 — x >= 0 (rightarrow) x <= 8
Решим уравнение:
8 — x = x2 — 5x + 11
x2 — 4x + 3 = 0
D = 16 — 12 = 4
(x_1 = frac{4 + 2}{2} = 3)
(x_2 = frac{4 — 2}{2} = 1)
Оба корня уравнения удовлетворяют условию x <= 8, значит, решением системы будут 1 и 3.
Рассмотрим вторую систему.
8 — x < 0 (rightarrow) x > 8
Решим уравнение:
8 — x = -x2 + 5x — 11
x2 — 6x + 19 = 0
D = 36 — 76 = -40 — при отрицательном дискриминанте решения уравнений нет.
Решением всего уравнения будут x = 1 и x = 3.
Ответ: 1, 3
4. Разберем еще один тип уравнений, когда модуль равен модулю. Неужели придется рассматривать целых 4 случая раскрытия модуля? Нет, достаточно будет возвести в квадрат обе части уравнения. Таким образом, мы получаем следующий переход:
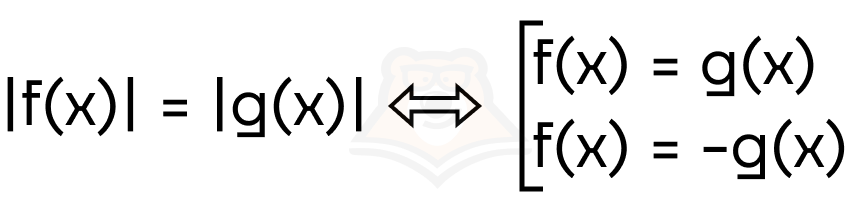
Пример 4. Решите уравнение |x — 2| = |2x + 8|.
Решение. Возведем обе части уравнения в квадрат. Для этого воспользуемся свойством 8.
(x — 2)2 = (2x + 
(x — 2)2 — (2x + 
Воспользуемся формулой сокращенного умножения:
((x — 2) — (2x + 8))((x — 2) + (2x + 
Если произведение множителей равно 0, то каждый множитель равен 0. Тогда:
x — 2 — (2x + 
x — 2 + (2x + 

Получаем совокупность:
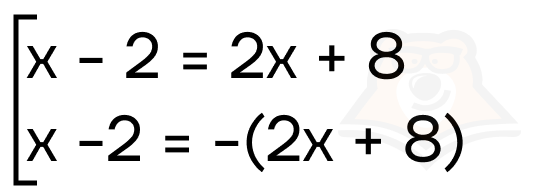
Решим первое уравнение совокупности:
x — 2 = 2x + 8
x = -10
Решим второе уравнение совокупности:
x — 2 = -2x — 8
3x = -6
x = -2
Решением уравнения будут x = -10 и x = -2
Ответ: -2, -10
Неравенства с модулем
Разобравшись, как решаются уравнения с модулем, можно приступать к неравенствам.
Пример 5. Решите неравенство x2 — |3x — 7| + 7 >= 0.
Решение. Найдем, при каких значениях х модуль равен 0. Получаем 3x = 7 (rightarrow) (x = frac{7}{3}).
Определим, с какими знаками модуль будет раскрываться на каждом промежутке.
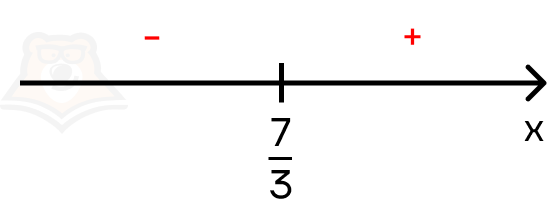
Осталось рассмотреть неравенство на двух промежутках.
1. (x leq frac{7}{3}), тогда
x2 — (-(3x — 7)) + 7 >= 0
x2 + 3x — 7 + 7 >= 0
x2 + 3x >= 0
x(x + 3) >= 0
Решим это неравенство «Методом интервалов». Сразу учтем ограничение (x leq frac{7}{3}).
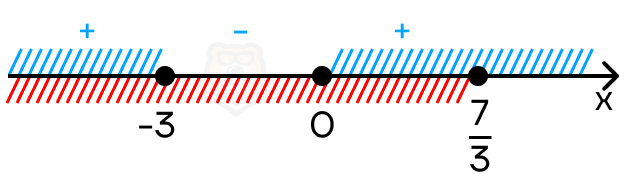
Получаем, что решением неравенства на заданном промежутке будет (x in (-infty; -3] U[0; frac{7}{3}]).
2. (x > frac{7}{3}), тогда
x2 — 3x + 7 + 7 >= 0
x2 — 3x + 14 >= 0
x2 — 3x + 14 = 0
D = 9 — 56 = -47 — корней на заданном отрезке не будет.
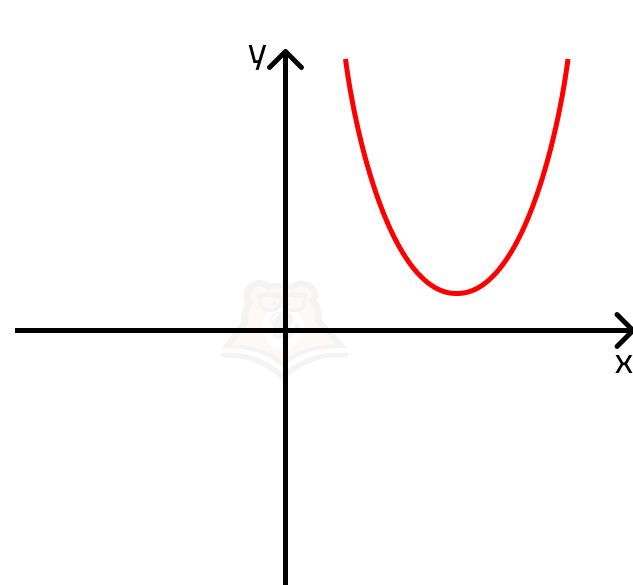
Вспомним, что корни квадратного уравнения — это точки пересечения параболы и оси х. Если парабола не пересекает ось х, то неизбежно лежит выше или ниже ее. Поскольку в нашем случае ветви параболы направлены вверх, мы можем нарисовать ее примерный график.
Так как парабола задается функцией y = x2 — 3x + 14, то неравенство будет выполняться при всех y >= 0. Парабола целиком попадает в эту область, а решением неравенства будет любое х.
Однако не стоит забывать про ограничение (x > frac{7}{3}). Накладывая его, получаем решение ((frac{7}{3}; + infty)).
Осталось только объединить полученные на промежутках решения:
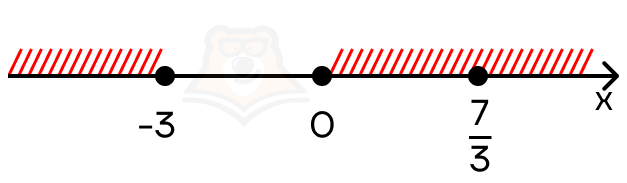
Получаем, что (x in (-infty;- 3] U [0; +infty)).
Ответ: (x in (-infty;- 3] U [0; +infty))
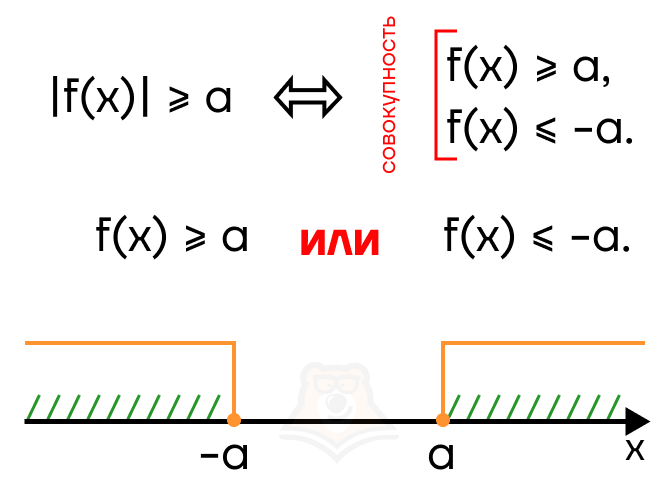
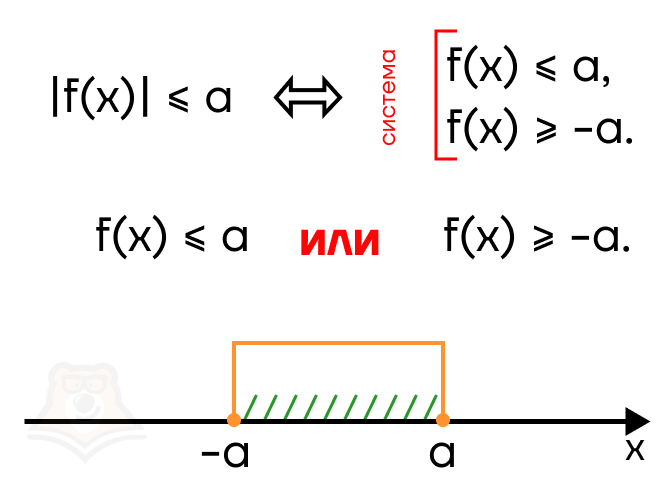
Рассмотрим неравенства вида |f(x)| > a и |f(x)| < a, где а — некоторое число и a >= 0. Модуль можно раскрыть двумя способами и получить два неравенства. Но будет это совокупность или система?
Это зависит от знака. Разберем случай |f(x)| > a. Заметим, что строгость знака может быть любой. Тогда модуль раскрывается как:
f(x) > a и -f(x) > a (rightarrow) f(x) < -a.
Отметим эти промежутки на числовой прямой:
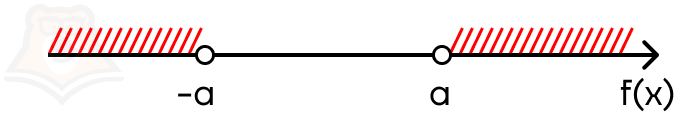
В ответе должны оказаться оба промежутка — их нужно объединить. В этом случае модуль раскрывается в совокупности.
Рассмотрим случай |f(x)| < a, здесь строгость знака также может быть любой. Раскроем модуль: f(x) < 0 и -f(x) < a (rightarrow) f(x) > -a. На числовой прямой это будет выглядеть следующим образом:

В в ответе должен оказаться промежуток от —а до а. Следовательно, необходимо воспользоваться системой, чтобы “отсечь” лишние промежутки.
Можно ли обойтись в этом случае без раскрытия модуля? Да, но необходимо возвести неравенство в квадрат.
|f(x)| ⋁ a | (uparrow) 2 — вместо ⋁ может стоять любой знак неравенства.
f2(x) ⋁ a2
f2(x) — a2 ⋁ 0
Воспользуемся формулой сокращенного умножения:
(f(x) — a)(f(x) + a) ⋁ 0
Однако стоит помнить, что обе части неравенства можно возвести в квадрат только в том случае, если они неотрицательны. То есть обязательно должно выполняться условие a0.
Мы получили равносильный переход. Но существуют ли равносильные переходы, если вместо числа а стоит другая функция или даже модуль? Да. Они выводятся таким же способом, как и переход для неравенства с числом. Получаем еще два равносильных перехода:
- |f(x)| ⋁ g(x) (rightarrow) (f(x) — g(x))(f(x) + g(x)) ⋁ 0
g(x) обязательно должно быть неотрицательным, чтобы можно было возвести неравенства в квадрат.
- |f(x)| ⋁ |g(x)| (rightarrow) (f(x) — g(x))(f(x) + g(x)) ⋁ 0
Разберем на примере, как можно использовать равносильный переход. Для этого возьмем то же неравенство, что и в примере 5, но решим его по-другому.
Пример 6. Решите неравенство x2 — |3x — 7| + 7 >= 0.
Решение. Перенесем модуль в другую часть неравенства:
|3x — 7| <= x2 + 7. Модуль всегда неотрицателен. Правая часть неравенства неотрицательна, поскольку число в квадрате всегда положительно.
Повторим действия, чтобы прийти к равносильному переходу:
(3x — 7)2 <= (x2+7)2
(3x-7)2 — (x2 + 7)2 <= 0
(3x — 7 — (x2 + 7))(3x — 7 + x2 + 7) <= 0
(3x — 7 — x2 — 7)(3x + x2) <= 0
(-x2 + 3x — 14) * x(3 + x) <= 0
-(x2 — 3x + 14) * x(3 + x) <= 0
(x2 — 3x + 14) * x(3 + x) <= 0
Рассмотрим первую скобку:
x2 — 3x + 14 = 0
D = 9 — 56 = -47 — корней нет. Выражение всегда будет положительно, то есть на него можно разделить все неравенство. Получаем:
x(3 + x) <= 0

Тогда (x in (-infty;- 3] U [0; +infty))
Ответ: (x in (-infty;- 3] U [0; +infty))
При решении можно сразу использовать равносильный переход, не расписывая его.
Итак, неравенства с модулем можно решить двумя способами: раскрывать модуль и воспользоваться равносильным переходом. Выбор способа зависит от личных предпочтений и удобства решения.
Фактчек
- Модуль — расстояние от любой точки на координатной прямой до начала координат. Модуль обозначается двумя вертикальными черточками: |a| = a и |-a| = a.
- Модулем числа называют выражение:

- График модуля представляет собой “галочку”, которая лежит выше оси х. Модуль отражает график любой функции зеркально оси х так, что значения у всегда больше 0.
- Модуль можно раскрыть двумя способами. Этим свойством можно пользоваться при решении уравнений с модулем.
- При решении неравенств с модулем можно раскрывать его, либо воспользоваться равносильным переходом, если в неравенстве выполняются все условия для него.
Проверь себя
Задание 1.
Чему равно выражение |-16 * 2|?
- 32
- −32
- −16
- 16
Задание 2.
Какой график имеет функция y = |x|?
- Парабола
- Гипербола
- Прямая
- Галочка
Задание 3.
Решите уравнение |x| = -3.
- 3
- −3
- Решений нет
- 3 и −3
Задание 4.
Решите уравнение |x + 2| = 15.
- −13
- 17
- 13 и -17
- Решений нет
Задание 5.
Какой равносильный переход можно использовать для неравенства вида |f(x) |⋁ |g(x)|?
- f(x) ⋁ g(x)
- f(x) ⋀ g(x)
- f2(x) — 2 * f(x) * g(x) + g2(x) ⋁ 0
- (f(x) — g(x))(f(x) + g(x)) ⋁ 0
Ответы: 1. — 1 2. — 4 3. — 3 4. — 3 5. — 4
оксана николаевна кузнецова
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Модуль числа
Модуль числа а обозначают $|a|$. Вертикальные черточки справа и слева от числа образуют знак модуля.
Например, модуль любого числа (натурального, целого, рационального или иррационального) записывается так: $|5|$, $|-11|$, $|2,345|$, $|sqrt[4]{45}|$.
Определение 1
Модуль числа a равен самому числу $a$, если $a$ является положительным, числу $−a$, если $a$ является отрицательным, или $0$, если $a=0$.
Данное определение модуля числа можно записать следующим образом:
$|a|= begin{cases} a, & a > 0, \ 0, & a=0,\ -a, &a
Можно использовать более краткую запись:
$|a|=begin{cases} a, & a geq 0 \ -a, & a
Пример 1
Вычислить модуль чисел $23$ и $-3,45$.
Решение.
Найдем модуль числа $23$.
Число $23$ – положительное, следовательно, по определению модуль положительного числа равен этому числу:
$|23|=23$.
Найдем модуль числа $–3,45$.
Число $–3,45$ – отрицательное число, следовательно согласно определению модуль отрицательного числа равен числу, противоположному данному:
$|-3,45|=3,45$.
Ответ: $|23|=23$, $|-3,45|=3,45$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 2
Модуль числа является абсолютной величиной числа.
Таким образом, модуль числа – число под знаком модуля без учета его знака.
Модуль числа как расстояние
Геометрическое значение модуля числа: модуль числа – это расстояние.
Определение 3
Модуль числа a – это расстояние от точки отсчета (нуля) на числовой прямой до точки, которая соответствует числу $a$.
Пример 2
Например, модуль числа $12$ равен $12$, т.к. расстояние от точки отсчета до точки с координатой $12$ равно двенадцати:
$|12|=12$.
Точка с координатой $−8,46$ расположена от начала отсчета на расстоянии $8,46$, поэтому $|-8,46|=8,46$.
«Модуль числа, сравнение чисел» 👇
Модуль числа как арифметический квадратный корень
Определение 4
Модуль числа a является арифметическим квадратным корнем из $a^2$:
$|a|=sqrt{a^2}$.
Пример 3
Вычислить модуль числа $–14$ с помощью определения модуля числа через квадратный корень.
Решение.
$|-14|=sqrt{((-14)^2}=sqrt{(-14) cdot (-14)}=sqrt{14 cdot 14}=sqrt{(14)^2}=14$.
Ответ: $|-14|=14$.
Сравнение отрицательных чисел
Сравнение отрицательных чисел основывается на сравнении модулей этих чисел.
Замечание 1
Правило сравнения отрицательных чисел:
- Если модуль одного из отрицательных чисел больше, то такое число является меньшим;
- если модуль одного из отрицательных чисел меньше, то такое число является большим;
- если модули чисел равны, то отрицательные числа равны.
Замечание 2
На числовой прямой меньшее отрицательное число располагается левее большего отрицательного числа.
Пример 4
Сравнить отрицательные числа $−27$ и $−4$.
Решение.
Согласно правилу сравнения отрицательных чисел найдем сначала модули чисел $–27$ и $–4$, а затем сравним полученные положительные числа.
$|-27|=27$
$|-4|=4$
Сравним полученные натуральные числа:
$27 > 4$.
Таким образом, получаем, что $–27 |-4|$.
Ответ: $–27
При сравнении отрицательных рациональных чисел необходимо преобразовать оба числа к виду обыкновенных дробей или десятичных дробей.
Сравнение чисел с противоположными знаками
Замечание 3
Правило сравнения чисел с противоположными знаками:
Положительное число всегда больше отрицательного, а отрицательное число всегда меньше положительного.
Пример 5
Сравнить целые числа $−53$ и $8$.
Решение.
Числа имеют противоположные знаки. Согласно правилу сравнения чисел с противоположными знаками получаем, что отрицательное число $−53$ меньше положительного числа $8$.
Ответ: $−53
Пример 6
Сравнить числа $3 frac{11}{13}$ и $–5,(123)$.
Решение.
Согласно правилу сравнения чисел с противоположными знаками отрицательное число всегда меньше положительного. Следовательно, $–5,(123)
Ответ: $–5,(123)
По данному правилу можно сравнивать также и действительные числа с противоположными знаками.
Если числа заданы как числовые выражения, то сразу невозможно определить какие они имеют знаки. В таком случае нужно вычислить значение этих выражений и затем определить, какое из правил сравнения можно применить.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме