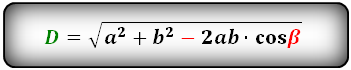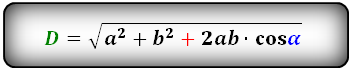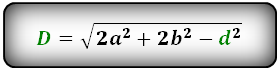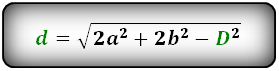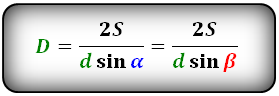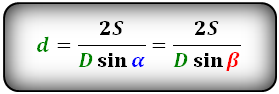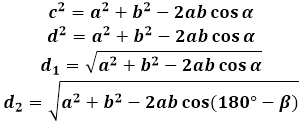Диагональ параллелограмма можно найти, точнее её половину, как сторону треугольника. Значит нужно знать по крайней мере еще две величины (если получается прямоугольный треугольник) или три (2 стороны и угол).
Вот формулы для определения длины меньшей диагонали d:
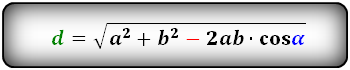
d = √a^2 + b^2 + 2ab·cosβ, d = √a^2 + b^2 — 2ab·cosα, где a и b — стороны параллелограмма, а β больший угол, α — меньший угол, D — длина большей диагонали.
1
Как найти меньшую диагональ параллелограмма?
Как найти меньшую диагональ параллелограмма?
1 ответ:
0
0
Диагональ параллелограмма можно найти, точнее её половину, как сторону треугольника. Значит нужно знать по крайней мере еще две величины (если получается прямоугольный треугольник) или три (2 стороны и угол).
Вот формулы для определения длины меньшей диагонали d:
d = √a^2 + b^2 + 2ab·cosβ, d = √a^2 + b^2 — 2ab·cosα, где a и b — стороны параллелограмма, а β больший угол, α — меньший угол, D — длина большей диагонали.
Читайте также
- Да, биссектрисы смежных углов параллелограмма перпендикулярны. Объяснение: сумма смежных углов параллелограмма равна 180 градусам, значит сумма их половинок равна 90 градусов. Это значит, что третий угол треугольника,образов<wbr />анного пересечением биссектрис равна тоже 90 градусам, то есть они перпендикулярны.
- Если ВК = 2, и сторона АВ тоже равна 2, так как биссектрисы перпендикулярны и они при пересечении со сторонами ВС м АD образуется ромб. Так как CL=CD+DL, то DL=6-4=2 DL=KC. Значит ВС=6, тогда периметр равен 2*(4+6)=20.
- Да, диагональ АС=7. Объяснение. Высота ВН равна 3V3/2, так как АН равна 1,5 (как сторона лежащая против угла в 30 градусов). Если опустить перпендикуляр СМ=ВН на сторону АД, то получим прямоугольный треугольник АСМ. AM=AC+CM=5+1,5=6,5. АС гипотенуза, по теореме Пифагора АС^2=AM^2+CM^2=169/4 + 27/4 = 196/4=49. Поэтому АС=7.
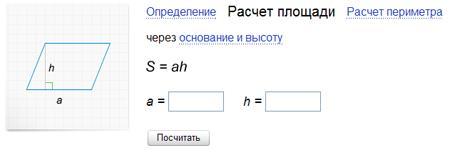
Так как площадь параллелограмма вычисляется по формуле
<h2>S = |a |*|b | * sin (a)/ (b) </h2>
где в формуле использованы модули векторов a , b и угол между этими векторами.
А эта формула есть не что иное , как векторное произведение двух векторов.
То есть площадь параллелограмма , построенного на двух векторах не что иное , как векторное произведение этих векторов.
Площадь параллелограмма находится через произведение длины основания a на высоту h. S = a * h.
Если это школьная задачка, в которой высота не известна, то должен быть известен какой-то другой параметр, через который можно вычислить высоту.
Если будет более конкретный вопрос, то тогда можно будет дать более конкретный ответ.
При известных длинах двух смежных сторон и угле между ними площадь параллелограмма находится очень просто. Вот формула:
S = a * b * sin (alfa)
где
S — площадь параллелограмма (искомая);
a, b — длины двух смежных, то есть соседних, соприкасающихся сторон. Обычно буквой a обозначают бо́льшую сторону, буквой b — меньшую;
alfa — величина угла между сторонами a и b.
Пример. Стороны параллелограмма равны 7 см и 6 см, а угол между ними равен 30°. Тогда площадь нашей фигуры будет равна: S = 7 см * 6 см * sin 30° = 21 (см^2).
<h2>Площадь параллелограмма</h2>
Простые геометрические расчеты, такие как нахождение площади параллелограмма, можно производить при помощи Яндекса. Наберите в Яндексе:
площадь параллелограмма
Яндекс предложит следующий интерфейс, в который нужно будет подставить значения:
<h2>Формула площади параллелограмма</h2>
S=ah
где «a» — основание, «h» — высота.
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
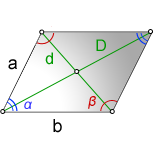
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α, β — углы параллелограмма
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (D, d):
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
S — площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 03 ноября 2011
-
Обновлено: 13 августа 2021
Вычислите длины диагоналей параллелограмма, построенного на векторах a = 2m + n и b = m — 2n , где m и n ― единичные векторы, угол между которыми o 60 ?
Математика | 10 — 11 классы
Вычислите длины диагоналей параллелограмма, построенного на векторах a = 2m + n и b = m — 2n , где m и n ― единичные векторы, угол между которыми o 60 .
d1 = 2m + n + m — 2n = 3m — n
|d1|² = (3m — n)(3m — n) = 9m² — 6mn + n² = 9|m|² — 6|m||n|cosa + |n|² = 9 * 1 — 6 * 1 * 1 * 1 / 2 + 1 = 9 — 3 + 1 = 7
d2 = 2m + n — m + 2n = m + 3n
|d2|² = (m + 3n(m + 3n) = m² + 6mn + 9n² = |m|² + 6|m||n|cosa + 9|n|² = 1 + 6 * 1 * 1 * 1 / 2 + 9 * 1 = 1 + 3 + 9 = 13.
Вычислить длины диагоналей и площадь параллелограмма, построенного на векторах : Полное решение?
Вычислить длины диагоналей и площадь параллелограмма, построенного на векторах : Полное решение.
Параллелограмм построен на векторах а = (1 ; 2 ; — 3) b = (2 ; — 1 ; — 1), нужно определить косинус угла между диагоналями и найти длину высоты, опущенной на вектор а?
Параллелограмм построен на векторах а = (1 ; 2 ; — 3) b = (2 ; — 1 ; — 1), нужно определить косинус угла между диагоналями и найти длину высоты, опущенной на вектор а.
Найдите координаты вектора единичной длины, коллинеарного прямой 3x — 2y + 1 = 0?
Найдите координаты вектора единичной длины, коллинеарного прямой 3x — 2y + 1 = 0.
Дан параллелограмм ABCD?
Дан параллелограмм ABCD.
Найдите сумму векторов вектор АВи АD.
Вычислить длину вектора а?
Вычислить длину вектора а.
Найдите а вектор * в вектор если угол между векторами равен 45° ?
Найдите а вектор * в вектор если угол между векторами равен 45° .
Вектор а = √2, вектор в = 6.
Четырехугольник АВСD — параллелограмм , О — точка пересечения его диагоналей?
Четырехугольник АВСD — параллелограмм , О — точка пересечения его диагоналей.
Назовите вектор с началом О , равный вектору — OD.
Дана система координат Oe1e2 , причем |e1| = 2, |e2| = корень из 3 , угол между ними равен 5pi / 6 ?
Дана система координат Oe1e2 , причем |e1| = 2, |e2| = корень из 3 , угол между ними равен 5pi / 6 .
Найти угол между векторами a(1 ; 2) и b(2 ; 2) и площадь параллелограмма, построенного на векторах a и b.
Найдите угол между диагоналями параллелограмма построенного на векторах p = 2a — b b q = a + b как на сторонах если a и b единичные векторы и угол между векторами a и b = 60°?
Найдите угол между диагоналями параллелограмма построенного на векторах p = 2a — b b q = a + b как на сторонах если a и b единичные векторы и угол между векторами a и b = 60°.
Дан параллелограмм ABCD?
Дан параллелограмм ABCD.
Выразите вектор ba через векторы bc и ac.
На этой странице сайта размещен вопрос Вычислите длины диагоналей параллелограмма, построенного на векторах a = 2m + n и b = m — 2n , где m и n ― единичные векторы, угол между которыми o 60 ? из категории Математика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.
От 39 до 1 с шагом 2 будет 20 слагаемых. Их можно поделить по парам как : (39 — 37) + (35 — 33) + (31 — 29) + (27 — 25) + . + (11 — 9) + (7 — 5) + (3 — 1) Откуда видно, что каждое из слагаемых в скобках будет равно 2. Т. е. Всего будет 20 слагаем..
80х — 40 = 160 + 40х 80х — 40х = 40 + 160 20х = 200 х = 200 : 20 х = 10.
НОД (72 ; 120) = 2×2×2×3 = 24 120 = 2×2×2×3×5 72 = 2×2×2×3 НОД (792 ; 1188) = 2×2×3×3×11 = 396 792 = 2×2×2×3×3×11 1188 = 2×2×3×3×3×11 НОД (924 ; 396) = 2×2×3×11 = 132 396 = 2×2×3×3×11 924 = 2×2×7×3×11 НОД (116 ; 111) = 1 111 = 3×37 116 = 2×2×29 — — -..
Пусть х — площадь поля. 45% = 0, 45 х — 0, 45х = 165 0, 55х = 165 х = 165 : 0, 55 х = 16500 : 55 х = 300 (га) площадь поля. Ответ : 300 га.
45% = 0, 45 1)100% — 45% = 55% — 165га 55% = 0, 55 2)165 : 0, 55 = 300(га) — осталось вспахать Ответ : 300га.
(34 + 40) — c = 19 74 — c = 19 c = 74 — 19 c = 55 Ответ : 55.
74 — с = 19 с = 74 — 19 с = 55.
12•4 + 16 = 64(р. ) Ответ : 64 ребёнка смотрели цирковое представление.
4 * 12 = 48 48 + 16 = 64 ответ : 64 детей смотрело представление.
Диагонали параллелограмма
Параллелограмм — это четырехугольник, у которого по определению противоположные стороны параллельны и равны. Как следствие, противоположные углы параллелограмма также будут между собой равны, а так как сумма всех углов в четырехугольнике равна 360 градусам, то можно сделать вывод, что сумма двух последовательных углов будет равна 180 градусам. Данное свойство будет играть существенную роль для нахождения диагоналей параллелограмма, с учетом того, что они разной длины.
Так как каждая диагональ параллелограмма делит его на два равновеликих треугольника, именно их свойства и будут использованы для выведения формулы диагонали параллелограмма.
В любом треугольнике угол и сторона, лежащие напротив, пропорциональны друг другу. Для параллелограмма это будет значить, что более длинная диагональ будет лежать напротив тупого угла, а более короткая диагональ — напротив острого.С учетом того, что стороны треугольников, полученных в результате проведения диагоналей, одинаковы — это стороны параллелограмма, значение градусной меры угла между данными сторонами определяет чему будет равна длина диагонали,вычисленной по формуле. Другими словами, если в формулудиагонали подставить значение острого угла параллелограмма, то калькулятор вычислит длину короткой диагонали, а если подставить значение тупого угла — то длинной.
Для того чтобы перейти от одного угла к другому, используется разность 180 градусов и заданного угла, таким образом калькулятор одновременно может вычислить обе диагонали.
Чтобы вывести формулу диагонали параллелограмма, используется теорема косинусов в треугольнике, который диагональ образует со сторонами. В любом из подобных треугольников, диагональ является стороной, противолежащей углу параллелограмма и, соответственно, ее квадрат равен сумме квадратов двух других сторон треугольника (сторон параллелограмма, в данном случае) за вычетом удвоенного произведения тех же сторон на косинус приведенного угла. Чтобы найти длину диагонали параллелограмма, калькулятор вычисляет квадратный корень из данного выражения.
Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
- Векторная алгебра.
- Скалярное произведение векторов, свойства. Длина вектора. Угол между векторами.
Скалярное произведение векторов, свойства. Длина векторов. Угол между векторами.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Длина вектора.
Пусть вектор $overline a=(x, y, z)$ представлен своими координатами в прямоугольном базисе. Тогда его длину можно вычислить по формуле $$|overline a|=sqrt.$$
Скалярное произведение векторов.
Если заданы координаты точек $A(x_1, y_1, z_1) $ и $B(x_2, y_2, z_2),$ то координаты вектора $overline$ можно найти по формулам $$overline=(x_2-x_1, y_2-y_1, z_2-z_1).$$ Скалярным произведением ненулевых векторов $a_1$ и $a_2$ называется число $$(a_1, a_2)=|a_1||a_2|cos(widehat).$$
Для скалярного произведения наряду с обозначением $(a_1,a_2)$ используется также обозначение $a_1a_2.$
Геометрические свойства скалярного произведения:
1) $a_1perp a_2Leftrightarrow a_1a_2=0$ (условие перпендикулярности векторов).
2) Если $varphi=(widehat),$ то $$0leqvarphi 0; qquadqquad frac <pi>
Алгебраические свойства скалярного произведения:
2) $(lambda a_1)a_2=lambda (a_1 a_2);$
Если векторы $a_1(X_1, Y_1, Z_1)$ и $a_2(X_2, Y_2, Z_2)$ представлены своими координатами в прямоугольном базисе, то скалярное произведение равно $$a_1a_2=X_1X_2+Y_1Y_2+Z_1Z_2. $$
Из этой формулы, в частности, следует формула для определения косинуса угла между векторами:
Решение.
а) $$a_1^2=(a_1, a_1)=|a_1||a_1|cos(widehat)=|a_1|^2=3^2=9.$$
б) $(3a_1-2a_2)(a_1+2a_2);$
Поскольку скалярное произведение зависит от длин векторов и угла между ними, то заданные векторы можно выбрать произвольно учитывая эти характеристики. Пусть $a_1=(3; 0). $ Тогда вектор $a_2,$ имея длину $|a_2|=4,$ и, образуя угол $frac<2pi><3>$ с положительной полуосью оси $OX,$ имеет координаты $x=|a_2|cosfrac<2pi><3>=-frac<4><2>=-2; $
$3a_1-2a_2=3(3;0)-2(-2;2sqrt 3)=(9;0)-(-4; 4sqrt 3)=(13;-4sqrt 3);$
$a_1+2a_2=(3; 0)+2(-2;2sqrt 3) = (3; 0)+ (-4; 4sqrt 3)= (-1; 4sqrt 3).$
$(3a_1-2a_2)(a_1+2a_2)=(13; -4sqrt 3)(-1; 4sqrt 3) =-13-48=-61.$
в) $(a_1+a_2)^2.$
$a_1+a_2$=$(3; 0)+(-2; 2sqrt 3)=(1; 2sqrt 3).$
$(a_1+a_2)^2=(1; 2sqrt3) (1; 2sqrt 3)=1+12=13.$
Ответ: a) 9; б) -61; в) 13.
2.67. Вычислить длину диагоналей параллелограмма, построенного на векторах $a=p-3q, $ $b=5p+2q,$ если известно, что $|p|=2sqrt<2>, |q|=3, (widehat)=frac<pi><4>.$
Решение.
Способ 1.
Из треугольника $ABC$ имеем $AC=AB+BC=a+b=p-3q+5p+2q=6p-q.$
Зная длину векторов $p$ b $q$ и угол между этими векторами, можно найти длину вектора $AC$ по теореме косинусов:
Из треугольника $ABD$ имеем: $BD=AD-AB=b-a=5p+2q-p+3q=4p+5q.$
По теореме косинусов находим длину вектора $BD:$
$|BD|^2=|4p|^2+|5q|^2-8p5qcos widehat<(6p, q)>=$ $128+225+240=593.$
Пусть $q=(3; 0). $ Тогда вектор $p,$ имея длину $|p|=2sqrt 2,$ и образуя угол $frac<pi><4>$ с положительной полуосью оси $OX$ имеет координаты
Из треугольника $ABC$ имеем
Из треугольника $ABD$ имеем
$BD=AD-AB=b-a=5p+2q-p+3q=4p+5q=$ $=4(2; 2)+5(3;0)=(8; 8)+(15; 0)=(23; 8).$
Ответ: $15, sqrt <593>.$
2.68. Определить угол между векторами $a$ и $b$ если известно, что $(a-b)^2+(a+2b)^2=20$ и $|a|=1, |b|=2.$
Ответ: $2pi/3$
$|a_1|=3; |a_2|=5. $ Определить, при каком значении $alpha$ векторы $a_1+alpha a_2$ и $a_1-alpha a_2$ будут перпендикулярны.
Ответ: $alpha=pmfrac<3><5>$
В треугольнике $ABC$ $overline=3e_1-4e_2;$ $overline=e_1+5e_2.$ Вычислить длину его высоты $overline,$ если известно, что $e_1$ и $e_2$ взаимно перпендикулярные орты.
http://allcalc.ru/node/981
http://mathportal.net/index.php/vektornaya-algebra/skalyarnoe-proizvedenie-vektorov-svojstva-dlina-vektora-ugol-mezhdu-vektorami
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Найти меньшую диагональ параллелограмма
|
|||
|
Стороны параллелограмма равны 10 см и 13 см, высота, проведенная к меньшей стороне, равна 12 см. Найти меньшую диагональ параллелограмма. Можете помочь с проверкой задания. Я думаю, она легковата, так что извиняюсь за неё.
|
||
| Вернуться к началу |
|
||
|
issa |
Заголовок сообщения: Re: Найти меньшую диагональ параллелограмма
|
|
michel писал(а): а почему Вы так не уверены? Потому что я глупый, спасибо за ответ
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Вторая диагональ параллелограмма
в форуме Геометрия |
Elwoo |
2 |
661 |
02 июн 2016, 20:01 |
|
Как найти углы между диагоналями, зная диагональ и сторону?
в форуме Геометрия |
Senior Strateg |
11 |
1253 |
03 фев 2014, 16:12 |
|
Найти две вершины параллелограмма ABCD
в форуме Аналитическая геометрия и Векторная алгебра |
MarkusGronholm |
2 |
889 |
09 янв 2014, 18:56 |
|
Найти уравнения сторон параллелограмма
в форуме Аналитическая геометрия и Векторная алгебра |
lanvandance |
3 |
495 |
05 ноя 2018, 18:17 |
|
Найти длины диагоналей параллелограмма
в форуме Аналитическая геометрия и Векторная алгебра |
hard01 |
1 |
484 |
04 ноя 2014, 19:36 |
|
Найти координаты четвертой вершины параллелограмма
в форуме Аналитическая геометрия и Векторная алгебра |
ibelousov |
4 |
1359 |
28 янв 2015, 13:29 |
|
Диагональ четырёхугольника
в форуме Геометрия |
sfanter |
3 |
531 |
20 июл 2014, 07:29 |
|
Диагональ четырехугольника
в форуме Геометрия |
Shuna |
3 |
427 |
22 июл 2014, 15:08 |
|
Диагональ четырёхугольника по сторонам и площади
в форуме Геометрия |
aliakseika |
26 |
2806 |
21 фев 2017, 09:37 |
|
Диагональ ромба, Захар VS Пифагор
в форуме Палата №6 |
3axap |
295 |
5723 |
09 янв 2017, 18:55 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 2 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |