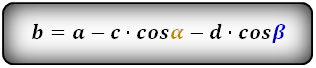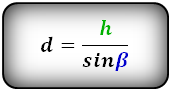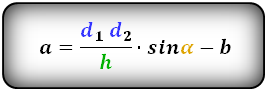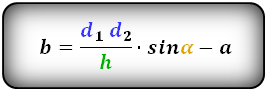Трапеция — это выпуклый четырехугольник с двумя параллельными основами и двумя непараллельными
боковыми сторонами.
Иногда фигура определяется как четырёхугольник, у которого пара противолежащих сторон параллельна,
поэтому параллелограмм и прямоугольник являются частными случаями трапеции. Также это
четырехугольник, у которого одна пара противоположных сторон параллельна, а остальные стороны не
равны между собой.
Параллельные стороны называются основами, а остальные боковыми.
Вычисление стороны необходимо для нахождения периметра, площади трапеции, ее диагоналей и других
значимых параметров.
- Длина основания через среднию линию и другое известное
основание - Нижнее основание через верхнее основание, высоту и углы при
нижнем основании - Верхнее основание через нижнее основание, высоту и углы при
нижнем основании - Нижнее основание через боковые стороны, верхнее основание и
углы при нижнем основании - Верхнее основание через боковые стороны, нижнее основание и
углы при нижнем основании - Боковую сторону через высоту и угол при нижнем
основании
Длина основания через среднюю линию и известное основание
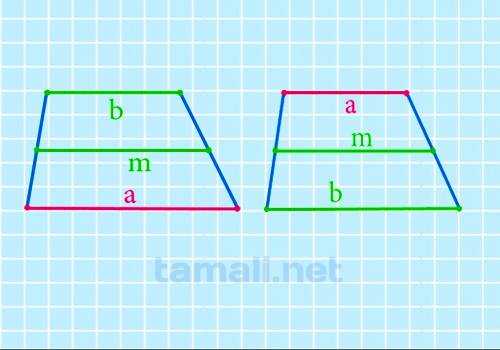
Средняя линия — отрезок, соединяющий середины боковых сторон фигуры. Через её значение
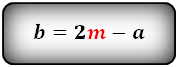
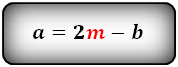
вычисляется одна из основ. Нужно умножить ее на два и вычесть известную:
a = 2m – b
Цифр после
запятой:
Результат в:
Например, средняя линия MN равна 6, а основание а – 9. Соответственно, значения, подставленные в
формулу, показывают, что b = 2*6 – 9 = 3.
Нижнее основание через верхнее основание, высоту и углы при нижнем основании
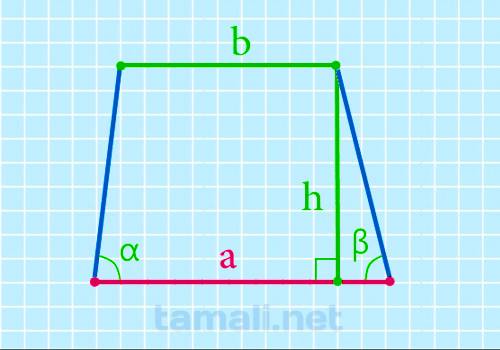
Высота h или BK – перпендикуляр, проведенный от одной основы к другой. Высота проводится в любой их
точке, но удобнее всего это делать из вершины углов при меньшей основе. Чтобы найти нижнее
основание, надо к верхнему прибавить произведение высоты на сумму котангенсов углов при нижнем:
a = b + h*(ctga + ctgb)
Цифр после
запятой:
Результат в:
Дано верхнее основание 10, высота 6 и углы 30 и 45. По формуле а = 10 + 6*(3+1) = 10 + 63 + 6 = 16+63.
Для равнобедренного четырёхугольника выведены две формулы. В первой (a = 2S/h – b) основа выражена с
помощью формулы площади. Пример: Площадь равнобедренной трапеции ABCD = 18, высота = 6, а AD = 5.
Найти BC. BC = 2*18/6 – 5 = 6 – 5 = 1
Второе выражение сформулировано следующим образом: (a = b + 2h*ctga). Высота АН в трапеции ADEF =
10, DE = 4, а DAF = 45 градусам. Найти AF: AF = 4 + 10*2*1 = 24
Верхнее основание через нижнее основание, высоту и углы при нижнем основании
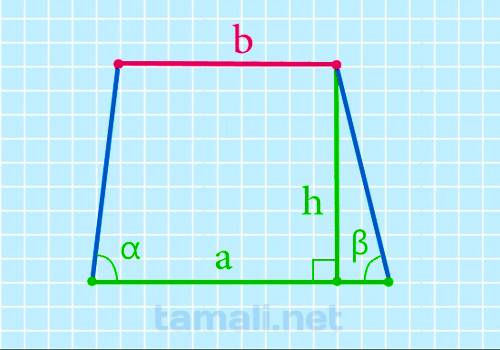
Чтобы найти верхнюю основу, надо из нижней вычесть произведение высоты на сумму котангенсов углов при
ней:
b = a – h*(ctg α + ctg β)
Цифр после
запятой:
Результат в:
Дана трапеция с нижним основанием 15, высотой 8 и углами в 45 градусов. По формуле а = 15 + 8*(1+1) =
15 + 16 = 31
Формулы для равнобедренного четырёхугольника: b = 2S/h – a и b = a – 2h*ctga.
- Площадь трапеции KLMN = 44, KL=MN, высота равна 8, KN = 5. Найти LM: LM = 44*2/8 – 5 = 6
- Высота трапеции DEFG = 15, DG= 5, а EDG = 45 градусам. Найти EF: EF = 5 + 15*2*1 = 35
Нижнее основание через боковые стороны, верхнее основание и углы при нижнем основании
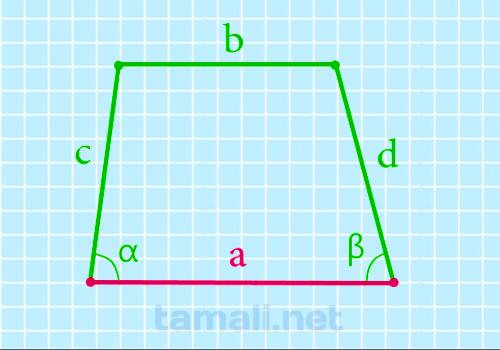
Для нахождения основы а нужно к основе b прибавить произведение одной и другой стороны и косинусов
углов при них
a = b + c * cos α + d * cos β
Цифр после
запятой:
Результат в:
Дана равнобокая трапеция с верхним основанием 6, боковыми сторонами 5 и 11 и углами в 45 градусов.
Найти нижнее основание: а = 6 + 5*2/2 + 11*2/2 = 6 + 162/2 = 6 + 82
Отдельно для подобного типа фигур было выведено два выражения: a = (d1^2 – c^2)/b и a = b +
2c*cosa.
- трапеции ABCD AB = CD = 8, диагональ AC = 12, а BC = 4. Вычислить AD: AD = (12*12 – 8*8)/4
= (144 – 64)/4 = 20 - В трапеции KLMN KL = MN = 4, LM = 7, а LKN равен 30 градусам. Вычислить KN: KN = 7 +
4*2*3/2 = 7 + 43
Верхнее основание через боковые стороны, нижнее основание и углы при нем
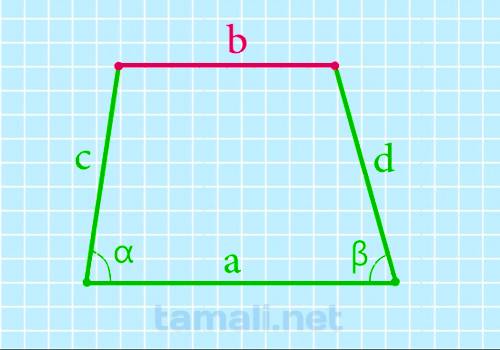
Для нахождения основы b нужно из основы а вычесть произведение одной и другой боковой стороны и углов
при них
b = a – c * cos α – d * cos β
Цифр после
запятой:
Результат в:
Дана трапеция с нижним основанием 27, боковыми сторонами 20 и 14 и углами в 30 и 60 градусов. Найти
верхнее основание: b = 27 — 20*3/2 — 14*1/2 = 27 — 103 — 7 = 20 —
103. Формулы для равнобедренного типа: b = (d1^2 — c^2)/a и b = a — 2c*cosa.
- В трапеции DEFG DE и FG = 11, диагональ АС = 13, а EF = 12. Вычислить DG: DG = (13*13 –
11*11)/12= (169 – 121)/12 = 4 - Боковые стороны трапеции BCDE BC и DE = 25, BE = 10, а CBE равен 60 градусам. Вычислить CD:
CD = 25 – 10*2*1/2 = 15
Боковая сторона через высоту и угол при нижнем основании
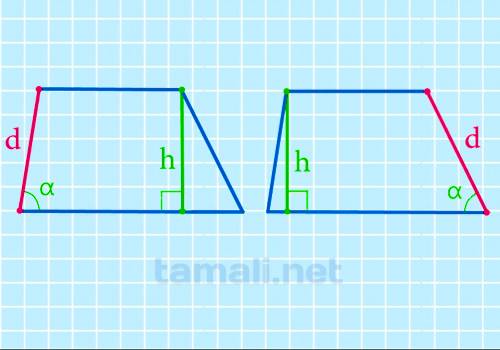
Чтобы найти боковую сторону, надо разделить высоту на синус угла при ней
d = h / sin α
Цифр после
запятой:
Результат в:
Дана трапеция с высотой 12 и углами в 30 и 60 градусов. Найти боковые стороны: c = 12/0,5 =
24, d = 12/3/2 = 243
Для прямоугольного типа формулы несколько отличаются. Самая простая из них связывает высоту и меньшую
боковую сторону: c = h.
Для нее существует еще несколько формул: с = d*sina; c = (a – b)*tga; c
= (d^2 – (a – b)^2)
- В прямоугольной трапеции CDEF сторона EF равна 22, а прилежащий угол = 45. Найти CD. CD =
22*2/2 = 112 - Прямоугольная трапеция MNOP имеет основания MP и NO, равные 32 и 19 соответственно. NMP равен 60
градусам. Найти MP: MP = (32 – 19)*3 = 133 - В прямоугольной трапеции ABCD AD и BC равны 35 и 15 соответственно. Диагональ АС = 26. Найти AB.
AB = (26^2 – (35 – 15)^2) = 676 – 400 = 276 = 269
Первая вытекает из прямоугольного треугольника и свидетельствует о том, что отношение катета к
гипотенузе равно синусу противолежащего угла. В этом треугольнике второй катет равен разности двух
оснований. Отсюда возникает утверждение, приравнивающее тангенс угла к отношению катетов. Третья
формула выведена на основании теоремы Пифагора.
Для второй боковой стороны выведено и записано три выражения: d = (a — b)/cosa; d = c/sina; d =
(c^2 — (a — b)^2). Первое и второе получаются из соотношения сторон в прямоугольном
треугольнике, а третье выводится из теоремы Пифагора.
- В прямоугольной трапеции KLMN KN = 28, LM = 13 а прилежащий угол = 30. Найти KL: KL = (28 –
13)/3/2 = 103 - В прямоугольной трапеции EFGH EF равна 45. FEH равен 30 градусам. Найти GH: GH = 45/0,5 =
90 - В прямоугольной трапеции NOPQ NQ и OP =.36 и 17. Диагональ равна 29. Найти NO: NO = (29^2 –
(36 – 17)^2) = 841 – 361= 480 = 430
Для равнобокой трапеции существуют формулы c = d1^2 – ab; c = (a – b)/2cosa; c = S/m*sina; c =
2S/(a+b)*sina.
- В трапеции LMNO LM = NO. LO = 16, MN = 6, диагональ равна 10. Найти LM: LM = 10^2 – 16*6 =
100 – 96 = 4 - Трапеция ABCD – равнобокая, AB = CD. AD = 18, BC = 4, а прилежащий угол равен 45 градусам. Найти
AB: AB = (18 – 4)/2/2 = 14/2/2 = 14/2 - В трапеции BCDE BC=DE. Площадь фигуры равна 48, BE = 17, CD = 7, а CBE равен 30 градусам.
Вычислить BC: m = (17 – 7)/2 = 5, BC = 48/5*1/2 = 96/5 = 19,2 - Площадь равнобедренной трапеции KLMN = 90, основания KN и LM = 32 и 18 соответственно, а LKN =
60 градусов. Вычислить KL: KL = 2*90/(32 + 18)*3/2 = 360/503 = 129600/7500 = 17,28
Виды трапеций
Существуют следующие виды трапеций:
- Равнобедренная трапеция — фигура, у которой боковые стороны и углы при основании равны.
Диагонали также равны. Треугольники, образованные диагоналями и основой, являются
равнобедренными. Если диагонали взаимно перпендикулярны, то площадь равна квадрату высоты. Если
разделить обе основы пополам и повести через эти точки линию, то она будет осью геометрической
фигуры. Отрезки, последовательно соединяющие середины смежных сторон, образуют ромб. - Прямоугольная трапеция — фигура, у которой одна из боковых сторон перпендикулярна основам
и равна высоте. Два угла будут равны 90 градусам, и они всегда принадлежат смежным вершинам, а
другие всегда острый и тупой, их сумма всегда будет равна 180 градусам. Каждая диагональ
образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из
вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, другая прямоугольный
треугольник. - Разносторонняя трапеция — фигура, боковые стороны которой не равны и углы при основании не
являются прямыми. Ее диагонали делят фигуру на четыре треугольника, два из которых подобны, а
остальные — равновелики, то есть имеют одинаковые площади. Сумма углов при боковой стороне 180
градусов.
Свойства трапеции
- Средняя линия параллельна основаниям и равна их полусумме.
- Любая биссектриса, выведенная из угла четырёхугольника, отсекает на основании (продолжении)
отрезок с длиной боковой стороны. - Треугольники AOD и COD, образованные отрезками диагоналей и основами, подобны.
Коэффициент
подобия – k = AD/BC.
Отношение площадей треугольников — k^2. - Треугольники ABO и DCO, образованные отрезками диагоналей и боковыми сторонами, имеют одинаковую
площадь. - В трапецию можно вписать окружность, если сумма оснований равняется сумме её боковых сторон.
- Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений
боковых сторон лежат на одной прямой. - Отрезок, соединяющий середины диагоналей, равняется половине разности основ и лежит на средней
линии.
Как найти меньшую сторону трапеции
Меньшим основанием трапеции является одна из ее параллельных сторон, имеющая минимальную длину. Рассчитать эту величину можно несколькими способами, используя те или иные данные.
Вам понадобится
- — калькулятор.
Инструкция
Если известны две длины — большого основания трапеции и средней линии — используйте для расчета наименьшего основания свойство трапеции. Согласно нему, средняя линия трапеции тождественна полусумме оснований. В этом случае наименьшее основание будет равно разности удвоенной длины средней линии и длины большого основания данной фигуры.
Если известны такие параметры трапеции, как площадь, высота, длина большого основания, то расчет наименьшего основания данной фигуры ведите на основе формулы площади трапеции. В этом случае конечный результат получите путем вычитания из разности частного удвоенной площади и высоты такого параметра, как длина большого основания трапеции.
Длину наименьшей боковой стороны в прямоугольной трапеции высчитывайте по другой методике. Этот параметр будет равен произведению длины второй боковой стороны и синуса острого угла, прилежащего к ней. В тех же случаях, когда величина угла неизвестна, наименьшую боковую сторону приравнивайте к высоте трапеции и высчитывайте по теореме Пифагора. Наименьшую боковую сторону в прямоугольной трапеции находите с помощью теоремы косинусов: с²=a²+b²-2ab*cosα; где а, b, с представляют собой стороны треугольника; α является углом между сторонами а и b.
Видео по теме
Обратите внимание
Чтобы не ошибиться в вычислениях, значения синусов и косинусов берите из тригонометрических таблиц.
Полезный совет
Если трапеция является остроугольной фигурой, то ее наименьшее основание высчитывайте путем вычитания из разности длины большого основания такой величины, как произведение высоты на сумму котангенсов углов при большом основании.
Для тупоугольной фигуры малое основание высчитывайте путем вычитания из разности длины большого основания такой величины, как произведение высоты на сумму разность котангенсов острого и тупого углов при большом основании.
Источники:
- Трапеция (задачи про основания)
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти меньшую сторону трапеции
Меньшим основанием трапеции является одна из ее параллельных сторон, имеющая минимальную длину. Рассчитать эту величину можно несколькими способами, используя те или иные данные.
Если известны две длины — большого основания трапеции и средней линии — используйте для расчета наименьшего основания свойство трапеции. Согласно нему, средняя линия трапеции тождественна полусумме оснований. В этом случае наименьшее основание будет равно разности удвоенной длины средней линии и длины большого основания данной фигуры.
Если известны такие параметры трапеции, как площадь, высота, длина большого основания, то расчет наименьшего основания данной фигуры ведите на основе формулы площади трапеции. В этом случае конечный результат получите путем вычитания из разности частного удвоенной площади и высоты такого параметра, как длина большого основания трапеции.
Длину наименьшей боковой стороны в прямоугольной трапеции высчитывайте по другой методике. Этот параметр будет равен произведению длины второй боковой стороны и синуса острого угла, прилежащего к ней. В тех же случаях, когда величина угла неизвестна, наименьшую боковую сторону приравнивайте к высоте трапеции и высчитывайте по теореме Пифагора. Наименьшую боковую сторону в прямоугольной трапеции находите с помощью теоремы косинусов: с²=a²+b²-2ab*cosα; где а, b, с представляют собой стороны треугольника; α является углом между сторонами а и b.
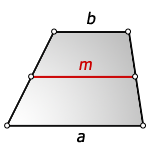
1. Формула длины основания трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :
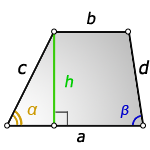
2. Формулы длины сторон через высоту и углы при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
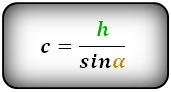
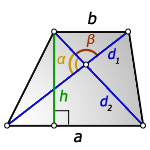
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 21 сентября 2013
-
Обновлено: 13 августа 2021
Как найти боковую сторону трапеции
Геометрия – наука, которую начинают изучать еще в школе. Ошибочно думать, что она никак не пригодится в жизни. Иногда необходимы точные размеры фигур, чтобы сделать, к примеру, WEB-дизайн помещения. А фигуры встречаются разные, в том числе и трапеции. Часто надо найти значения их боковых сторон или основания. Давайте в подробностях рассмотрим, как найти боковую сторону данного четырехугольника различной формы, если известны его углы, основания, диагонали, площадь и т.п.
1
Как найти боковую сторону трапеции, если известны основания?
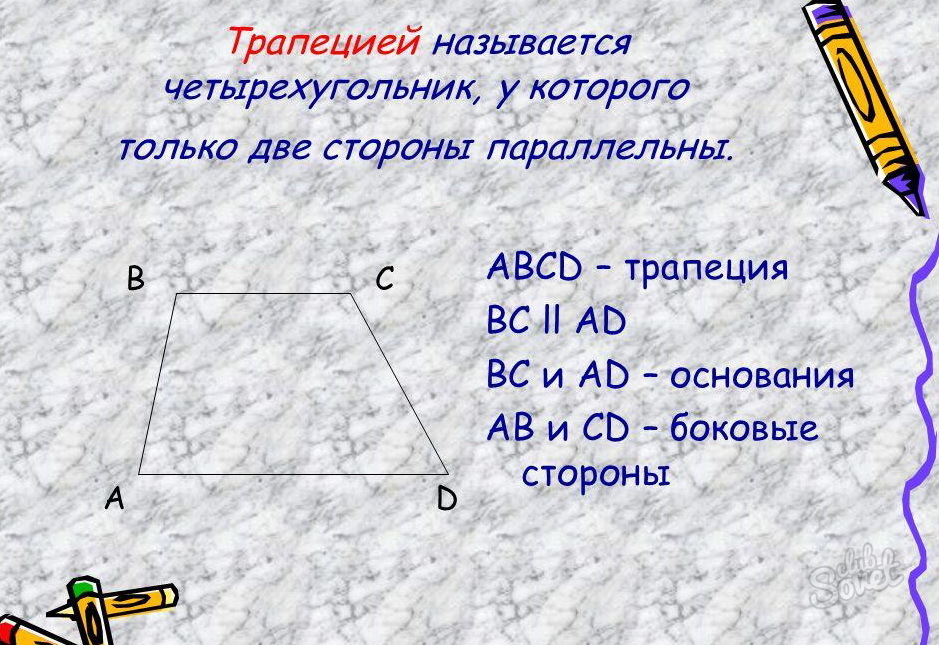
Трапеция – это четырёхугольник, у которого параллельны лишь две стороны. И эти не пересекающиеся отрезки называются основаниями данной фигуры. Трапеции бывают различных вариантов:
- Равнобокие – это те, у которых боковые стороны равны.
- Прямоугольные – имеют у основания один прямой угол.
- Остроугольные, разносторонние – с двумя острыми углами у основания.
- Тупоугольные, разносторонние – с одним тупым углом у основания.
Рассмотрим вариант нахождения боковой стороны (высоты) прямоугольной трапеции, если вам даны значения оснований.
Чтобы решить данную задачу, вам понадобится сделать следующее:
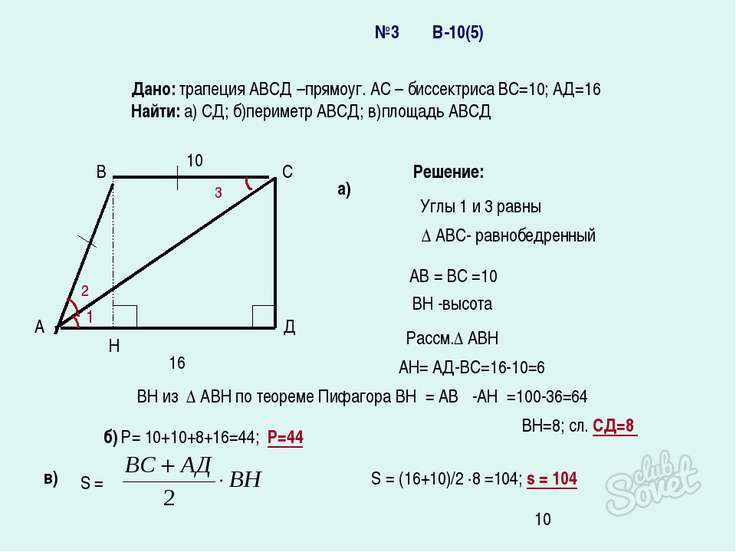
- Проведите вторую высоту – ВН в четырехугольнике.
- Получившийся отрезок ВН = СД, так как основание ВС параллельно АД.
- Образовавшийся треугольник АВС – равнобедренный, ведь АС – биссектриса, соответственно углы у основания равны и АВ = СВ = 10 см.
- Рассмотрим треугольник АВН, фактически у нас известны две стороны его: ВА и АН. АН = АД – CD = 16 – 10 = 6 см.
- Отсюда по теореме Пифагора: ВН² = АВ² – НА² = 64; ВН = 8 см, соответственно и СД тоже равно 8 сантиметров.
Кроме того, если вам известен угол ВАД, то СД = (АД – ВС) • tg α либо СД = АВ • sin α.
Большая боковая сторона рассчитывается по следующим формулам:
- АВ² = СД² + (АД – ВС)²
- АВ = (АД – ВС)/cos ∠ВАН
- АВ = CД/sin ∠ВАН
2
Как найти боковую сторону прямоугольной трапеции, если известны диагонали, площадь, средняя линия?
Если обозначить высоту трапеции – b, большую боковую сторону – c, основания – a и к, диагонали – d1 и d2. Больший угол между ними β, меньший – α, то высоту (боковую сторону трапеции) можно найти по следующим формулам:
b = d2 • d1/ (a + к) • sin α;
или же b = d2 • d1/ (a + к) • sin β
Для того чтоб определить b – меньшую сторону прямоугольной трапеции, с – большую сторону фигуры, с известными данными S – площадью, n – средней линией, применяйте следующие расчеты:
b = S/n = 2S/ (a + к)
с = S/n • sin α = 2S/ (a + к) • sin α
3
Как найти боковые стороны равнобедренной трапеции?
Итак, у равнобокой трапеции АВ = DC. Если вам даны различные величины, то боковые стороны можно найти по нижеприведенным формулам:
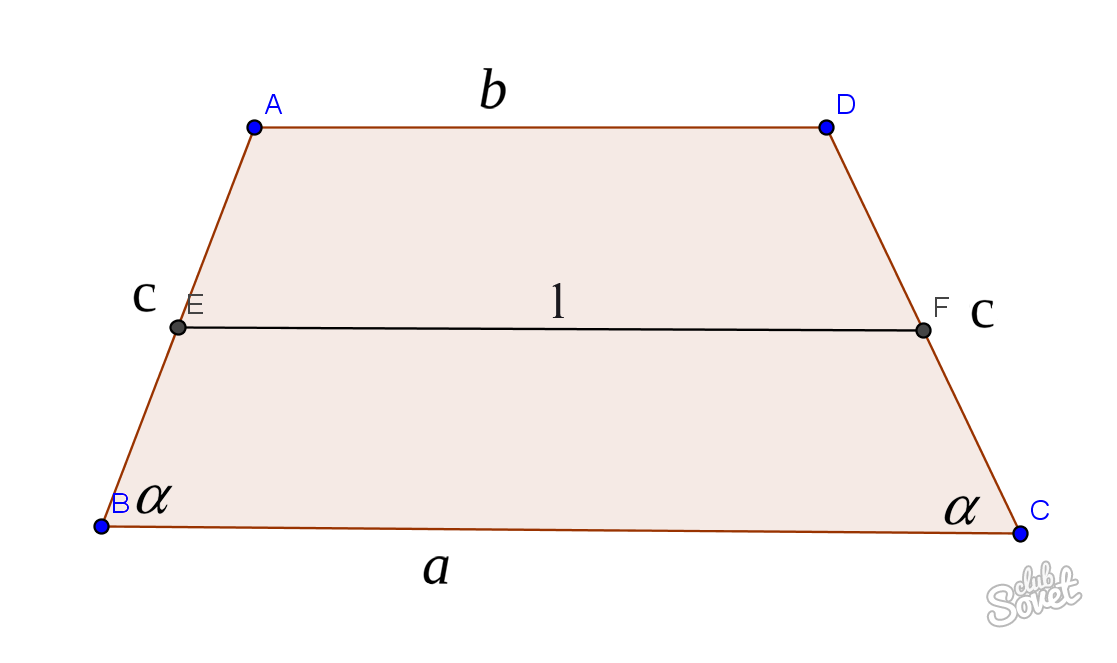
- если известны высота – h и угол – α, то АВ = DC = h/ sin α;
- если даны значения оснований и угол – α , то АВ = DC = (a – b)/ cos α;
- если даны диагонали d и основания, то АВ² = DC² = d² – b • a;
- если известны значения средней линии – l, площадь – S, углы – α либо – β (вверху возле основания b, то АВ = DC = S/ l • sin α = S/ l • sin α.
или же:
АВ = DC = S/ (b + a) • sin α = S/ (b + a) • sin β
В дальнейшем, если вы выучите формулы и научитесь верно рисовать чертежи данных фигур, то решить задачку по геометрии вам не составит труда. Ведь по правильной картинке ответ задачи практически виден сразу.