Как найти меньшую высоту параллелепипеда

Параллелепипед — это частный случай призмы, у которой основание и грани представляют собой параллелограмм.

Различают несколько разновидностей этой геометрической фигуры — прямой / прямоугольный параллелепипед, наклонный параллелепипед.

Высота параллелепипеда — это отрезок, который соединяет плоскости верхнего основания и нижнего основания параллелепипеда.

Высота перпендикулярна плоскости нижнего основания.

---

Для того, чтобы найти высоту параллелепипеда, можно воспользоваться традиционной формулой:

H = V / S.

H — высота параллелепипеда, V — объём параллелепипеда, S — площадь основания.

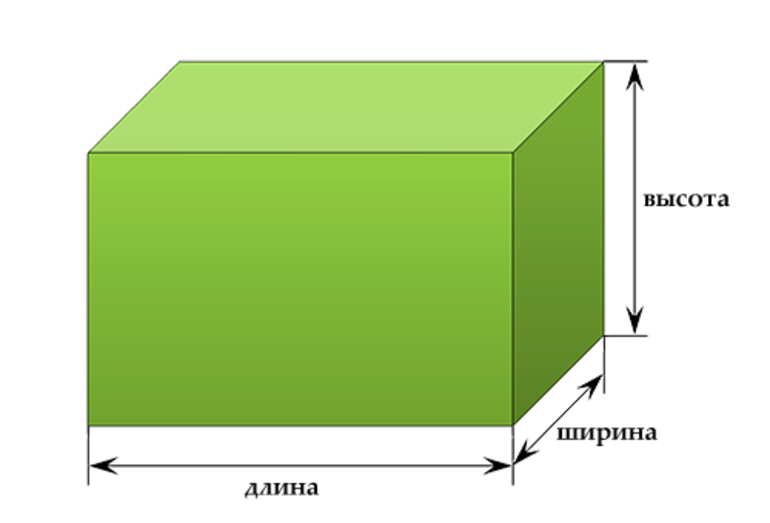
При этом объём параллелепипеда вычисляется по формуле: S = a * b * c, где a,b и c — это длины 3 измерений.

Что касается площади основания, то здесь может быть несколько случаев.

Если основание представляет собой параллелограмм, то S = a * b * sin(ab) — произведение 2 сторон на синус угла между ними.

Если мы имеем дело с прямоугольным параллелепипедом, то S = a * b — произведение 2 сторон.

Пример:

Боковое ребро наклонного параллелепипеда равно 10 см. Стороны основания равны 4 и 6 см, а угол между ними равен 30 градусов. Нужно найти высоту параллелепипеда.

1) V = 4 * 6 * 10 = 240 см3.

2) S = 4 * 6 * sin30° = 24 * 0,5 = 12 см.

3) H = V / S = 240 / 12 = 20 см.

Значит, высота параллелепипеда будет равна 20 см.

_

В случае с прямоугольным параллелепипедом всё немного проще.

Здесь высота будет совпадать с длиной грани (ребром) данной фигуры. Поэтому для нахождения высоты достаточно вычислить, чему равно боковое ребро.

Прямоугольный параллелепипед

Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

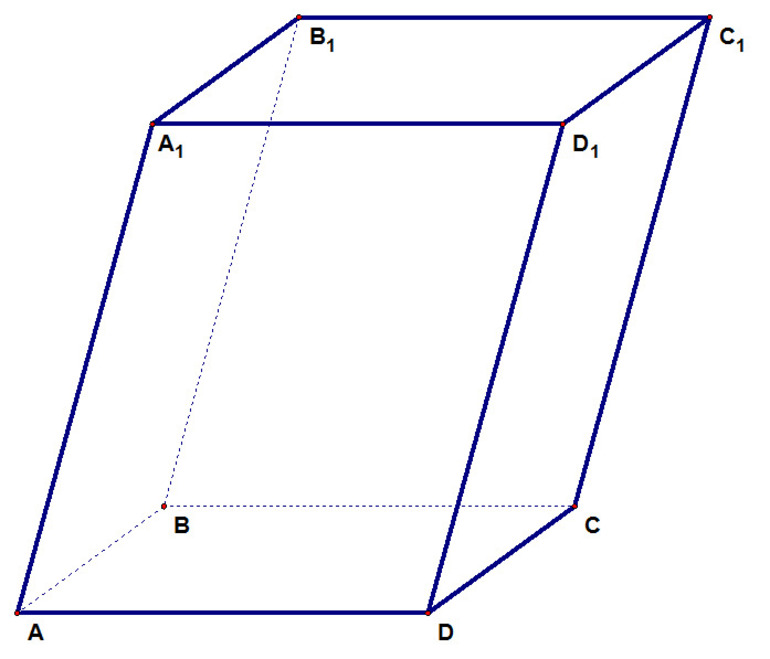
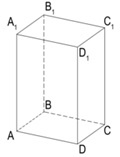
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.

Свойства прямоугольного параллелепипеда:

1. В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
2. Противоположные грани попарно равны и параллельны.
3. Все двугранные углы прямоугольного параллелепипеда – прямые.
4. Диагонали прямоугольного параллелепипеда равны.
5. Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

$с$ — высота(она же боковое ребро);

$P_<осн>$ — периметр основания;

$S_<осн>$ — площадь основания;

$S_<бок>$ — площадь боковой поверхности;

$S_<п.п>$ — площадь полной поверхности;

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

$S_<бок>=P_<осн>·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.

Дополнительные сведения, которые пригодятся для решения задач:

$а$ — длина стороны.

$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.

Пирамида

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Объем любой пирамиды равен трети произведения основания и высоты.

В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.

В основании лежит треугольник.

• $S=/<2>$, где $h_a$ — высота, проведенная к стороне $а$.
• $S=/<2>$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
• Формула Герона $S=√$, где $р$ — это полупериметр $p=/<2>$.
• $S=p·r$, где $r$ — радиус вписанной окружности.
• $S=/<4R>$, где $R$ — радиус описанной окружности.
• Для прямоугольного треугольника $S=/<2>$, где $а$ и $b$ — катеты прямоугольного треугольника.
• Для равностороннего треугольника $S=/<4>$, где $а$ — длина стороны.

В основании лежит четырехугольник.

1. Прямоугольник.
   $S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб.
   $S=/<2>$, где $d_1$ и $d_2$ — диагонали ромба.
   $S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
3. Трапеция.
   $S=<(a+b)·h>/<2>$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
4. Квадрат.
   $S=a^2$, где $а$ — сторона квадрата.

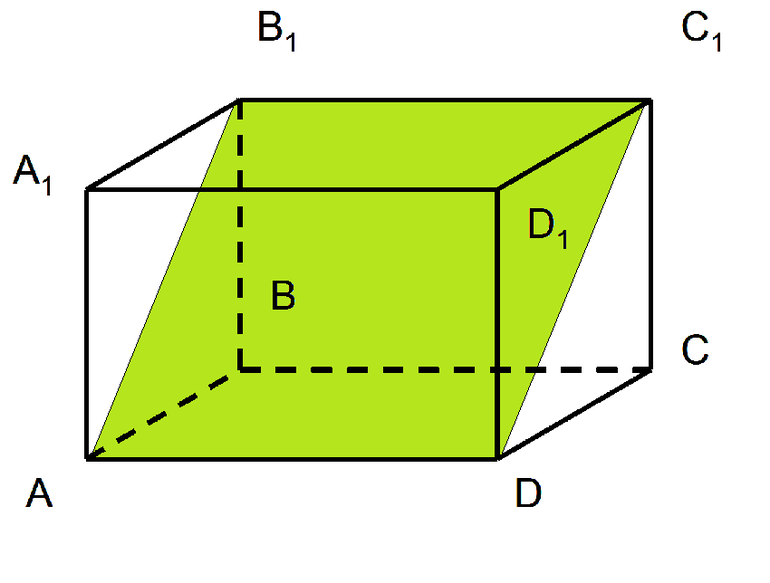
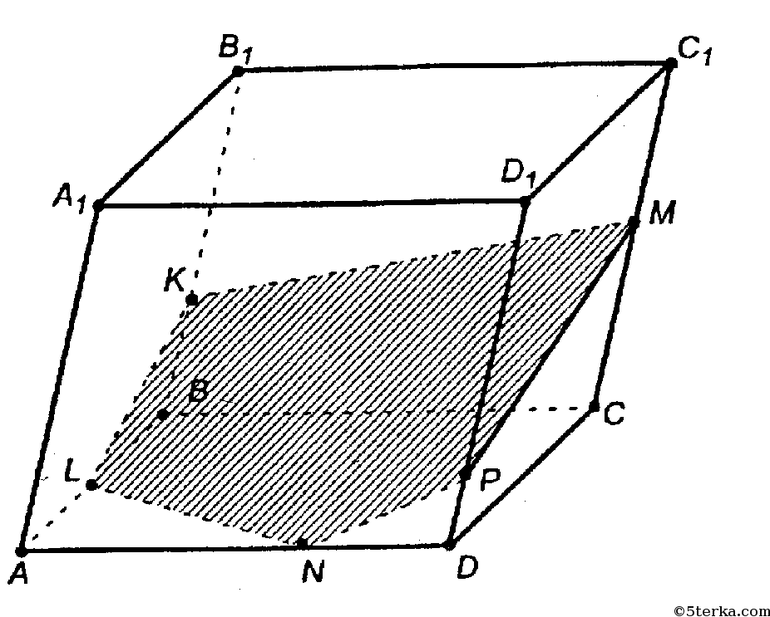
Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.

Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.

Объем пирамиды, в основании которой лежит прямоугольник

Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.

В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.

Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Прямоугольный параллелепипед. Что это такое?

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

1. Противолежащие грани параллелепипеда равны и параллельны друг другу.
2. Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
3. Параллелепипед симметричен относительно середины его диагонали.
4. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

1. Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
2. Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
3. Высота прямого параллелепипеда равна длине бокового ребра.
4. Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
5. Диагонали прямого параллелепипеда точкой пересечения делятся пополам.

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

• Площадь боковой поверхности прямого параллелепипеда
  Sб = Ро*h
  Ро — периметр основания
  h — высота
• Площадь полной поверхности прямого параллелепипеда
  Sп = Sб+2Sо
  Sо — площадь основания
• Объем прямого параллелепипеда
  V = Sо*h

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

1. Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
2. Противолежащие грани параллелепипеда попарно параллельны и равны.
3. Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
4. Диагонали прямоугольного параллелепипеда равны.
5. В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7. Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы прямоугольного параллелепипеда:

• Объем прямоугольного параллелепипеда
  V = a · b · h
  a — длина, b — ширина, h — высота
• Площадь боковой поверхности
  Sбок = Pосн·c=2(a+b)·c
  Pосн — периметр основания, с — боковое ребро
• Площадь поверхности
  Sп.п = 2(ab+bc+ac)

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

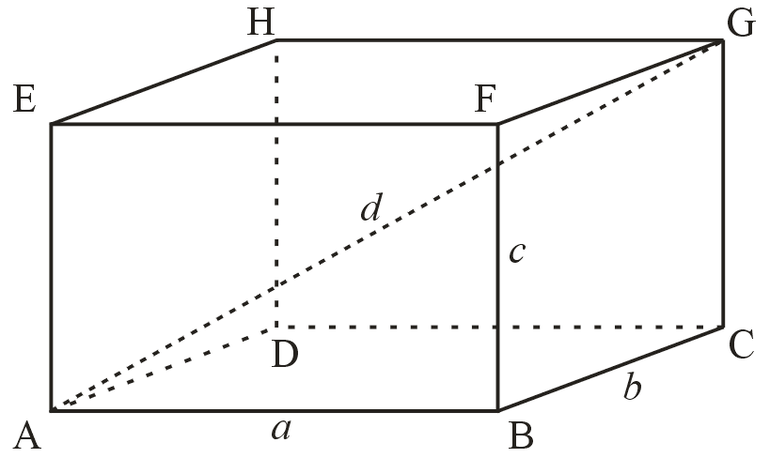
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = d₁² + c² = a² + b² + c²

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

1. В кубе 6 граней, каждая грань куба — квадрат.
2. Противолежащие грани параллельны друг другу.
3. Все углы куба, образованные двумя гранями, равны 90°.
4. У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
5. Диагонали куба равны.
6. Диагональ куба в √3 раз больше его ребра.
7. Диагональ грани куба в √2 раза больше длины ребра.

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

• Объем куба через длину ребра a
  V = a3
• Площадь поверхности куба
  S = 6a2
• Периметр куба
  P = 12a

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a — длина, b — ширина, c — высота. Тогда a = 10, b = 5, c = 8.

Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) — сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) — суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) — сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) — сумма длин всех ребер прямоугольного параллелепипеда.

Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X — сумма длин ребер).

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°.

По теореме Пифагора:
BD₁ 2 = DD₁ 2 + BD 2
BD 2 = BD₁ 2 – DD₁ 2
BD 2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD 2 = AD 2 + AB 2
AB 2 = BD 2 — AD 2 = (√17)2 — 4 2 = 1
A₁B₁ = AB = 1.

Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77
BD₁ = √77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

• прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
• параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
• основание прямоугольного параллелепипеда — прямоугольник;
• три измерения прямоугольного параллелепипеда: длина, ширина, высота;
• диагональ параллелепипеда равна сумме квадратов его измерений.

Параллелепипед — определение, свойства и измерение фигуры

Общая характеристика

В мире имеется множество предметов с формой параллелепипеда. Люди обычно не задумываются об этом, но архитектура и различные массивные строения состоят из нескольких граней. Выглядеть параллелепипед может по-разному в зависимости от типа.

Основные понятия и классификация

Определение параллелепипеда, пирамиды, куба и других многогранников было известно с древнейших времен. Основными характеристиками являются простота и значимость.

Выведенные формулы V и S значимы для решения различных задач с практическим содержанием и доказательства теорем (по чертежам). Виды параллелепипеда:

1. Прямой. Четыре боковые грани имеют углы по 90 градусов.
2. Прямоугольный. Каждая сторона фигуры является прямоугольной.
3. Наклонный.
4. Двугранный, трехгранный. Состоит из нескольких граней под углом 90 градусов.
5. Наклонный, диагональный. Боковые грани не перпендикулярны основаниям.
6. Ромбоэдр. Стороны являются одинаковыми ромбами.
7. Куб. Параллелепипед с равными (квадратными) сторонами.

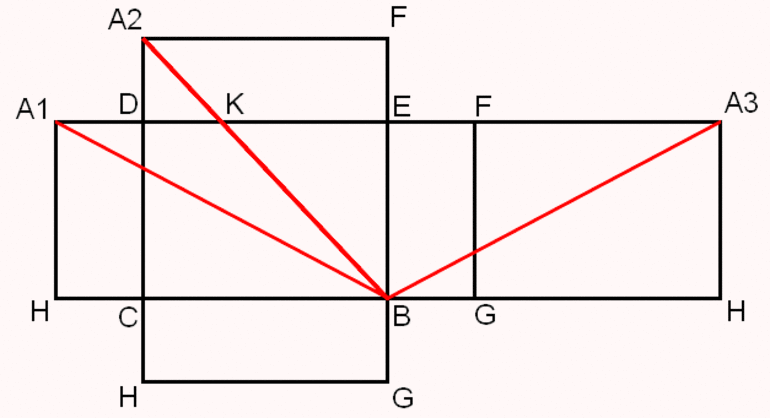
В 6 классе на уроке геометрии изучают планиметрию (плоские фигуры). Здесь представлена развертка плоскостей.

Две стороны параллелепипеда, не имеющие общего ребра, называются противоположными, а содержащие единую линию — смежными. С точки зрения плоскостей, расположенных параллельно, внутри пересекаются три их пары. Эти вершины соединяет отрезок — диагональ. Длина трех ребер правильного многогранника называется измерением. Главным условием является общая вершина.

При решении задач важно понятие высоты — перпендикуляра, опущенного из любой вершины на обратную сторону. Грань, на которую опускается высота, считается основанием. Свойства параллелепипеда:

• любые стороны являются параллелограммами (с симметрией);
• стороны, расположенные друг против друга, будут параллельными и равными.

Кирпич — отличный пример прямоугольного параллелепипеда (ПП). Также его форму имеют девятиэтажные панельные дома, шифоньеры, шкафы-купе, контейнеры для хранения продуктов и прочие предметы быта.

Диагонали поверхности пересекаются и этой центральной точкой делятся на несколько частей. Они равны d2=a2+b2+c2

Грани параллелепипеда спереди и сзади равнозначны, также как верхняя и нижняя стороны, но не равны, поскольку не противоположные, а смежные.

Формулы и анализ

Для ПП верно мнение, что его объем равен величине тройного произведения векторов трех сторон, исходящих из единой вершины. Формулы для ПП:

Расшифровка обозначений: V — объем фигуры, S — площадь поверхности, a — длина, b — ширина, c — высота.

Особым случаем параллелепипеда, в котором все стороны квадраты, является куб. Если любую из сторон обозначить буквой a, то для поверхности и объема используются формулы: S=6*a*2, V=3*а. В них V — объем фигуры, a — длина грани.

Последняя разновидность параллелепипеда — прямой тип. Его основанием будет параллелограмм, а основанием ПП — прямоугольник. Формулы, используемые в математике и геометрии: Sб=Ро*h, Sп=Sб+2Sо, V=Sо*h.

Для нахождения ответов недостаточно знать только свойства геометрической фигуры. Могут пригодиться формулы для вычисления S и V.

Диагональ ПП равна сложению квадратов его измерений: d2 = a2 + b2 + c2. Эта формула получается из теоремы Пифагора.

∆BAD — прямоугольный, поэтому BD2 = AB2 + AD2 = b2 + c2.

∆BDD1 является прямоугольным, значит, BD12 = BD2 + DD12. Нужно подставить значение: d2 = a2 + b2 + c2.

Стандартная формула: V= Sосн*h. Расшифровка обозначений: V — объем параллелепипеда, Sосн — площадь основания, h — высота.

S находится так же, как показатель параллелограмма или прямоугольника. При решении тестов и экзаменационных задач легче вычислять показатели призмы, в основе которой находится прямой угол. Также может пригодиться формула расчета стороны параллелепипеда Sбок = P*h, где:

• Sбок — площадь параллелепипеда;
• Р — периметр;
• h — высота, перпендикулярная основанию.

Объем фигуры равен величине смешанного произведения нескольких векторов, выпущенных из единой точки.

Практическое применение

Для вычисления объема, высоты и прочих характеристик фигуры нужно знать теоретические основы и формулы. Решение задач входит в программу сдачи ЕГЭ и билеты при поступлении в вуз.

Доказательство теорем

Теоретически S боковой поверхности ПП равна S б. п. = 2 (a+b)c. S полной поверхности равна Sполн. поверхности ПП=2 (ab+ac+bc).

Объем ПП равен произведению трех его боковых частей, выходящих из единой вершины (три измерения ПП): abc.

Доказательство: так как у ПП боковые ребра перпендикулярны основанию, то они являются и его высотами — h=AA1=c. Если в основании лежит прямоугольник, то Sосн=AB ⋅ AD=ab. Диагональ d ПП можно найти по формуле d2=a2+b2+c2, где a, b, c — измерения ПП.

Если в основании расположен прямоугольник, то △ ABD прямоугольный, значит, по теореме Пифагора BD2=AB2+AD2=a2+b2. Если все боковые грани перпендикулярны основной линии, то BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD.

Когда △ BB1D прямоугольный, то по теореме Пифагора B1D=BB12+BD2.

Решение задач

Задача 1: известны ПП: 3, 4, 12 см, необходимо найти длину главной диагонали фигуры.

Поиск ответа на вопрос начинается с выстраивания схематического изображения, на котором означаются величины. Используется формула B1D2 = AB2 + AD2 + AA12. После вычислений получается выражение b2=169, b=13.

Задача 2: ребра ПП, выходящие из общей точки, равны 3 и 4, общая S — 94. Нужно найти третье ребро, выходящее из той же вершины.

Ребра обозначаются а1 и а2, а неизвестное — а3. Площадь поверхности выражается S = 2 (a1a2 + a1a3 + a2a3).

Далее получаем a3 (a1 + a2) = S/2 — a1a2. Неизвестное ребро: a3 = S/2 — a1a2/a1 + a2 = 47−12/7 = 5.

Задача 3: два ребра прямоугольного параллелепипеда, выходящие из общей точки, составляют 72 и 18, диагональ равна 78. Нужно определить объем фигуры.

Для решения требуется найти диагональ по формуле вычисления квадратного корня из суммы (a2 + b2 + c2), где a, b, c — ребра фигуры. 78 — корень из суммы 722 + 182 + c2. Решение:

• 78 = корень из суммы 5508+с2
• 782 = 5508 + с2
• с2 = 6084 — 5508.
• С2 = 576.

Ответ: объем составляет 576.

Задача 4: ребро наклонного параллелепипеда составляет 10 см, прямоугольник KLNM с измерениями 5 и 7 см является сечением фигуры, параллельным ребру. Нужно определить площадь боковой поверхности призмы.

KL и AD не являются равными, как пара ML и DC. Боковая S фигуры эквивалентна S сечения, умноженной на AA1, так как ребро перпендикулярно сечению. Ответ: 240 см².

Задача 5: ABCDA1B1C1D1 = 3, 4 см, боковое ребро — 12 см. Нужно определить диагональ ПП.

В основании лежит прямоугольник со сторонами АВ 3 см и AD 4 см. Боковое ребро составляет 3 см. BB1 является высотой ПП и равняется 12 см. Диагональ B1D2 = AB2 + BB1 2 += 9+16+144 = 169. B1D= 13 см.

Задача 6: основанием ПП служит квадрат, одна из вершин его верхнего основания одинаково удалена от всех вершин нижней части. Нужно найти высоту фигуры, если диагональ основания равна 8 см, а боковое ребро — 5 см.

Одна из вершин основания (F) равнозначно удалена от всех вершин нижнего основания параллелепипеда. Вместе с диагональю нижней части (AC) она образует равнобедренный ∆AFC. AF = AC по условию. AF является ребром фигуры.

В равнобедренном ∆AFC стороны одинаковы: AF=FC=5 см, AC=8 см. Высота ∆AFC будет являться высотой параллелепипеда.

Высота треугольника делит его основание пополам. По теореме Пифагора она равна:

• FK2 + (AC/2)2 = FC2;
• FK2 + 16 = 25;
• FK2 =25−16 = 9;
• FK = 3 см.

Высота фигуры составляет 3 см.

Установленные теоремы, доказательства, а также выведенные формулы помогают вычислить различные значения для фигуры.

Геометрические фигуры. Прямоугольный параллелепипед.

Прямоугольный параллелепипед — прямой параллелепипед с прямоугольником в основании. У прямоугольного параллелепипеда каждая из шести граней является прямоугольником.

Примерами прямоугольного параллелепипеда являются спортивный зал, коробок спичек или системный блок компьютера.

Формулы прямоугольного параллелепипеда.

Прямоугольный параллелепипед с одинаковыми измерениями является кубом. Все 6 граней куба являются равными квадратами.

Обозначим длину ребра куба как n, тогда площадь 1-ой грани:

Площадь поверхности куба:

У прямоугольного параллелепипеда есть еще одно измерение – объем параллелепипеда (обозначается как V).

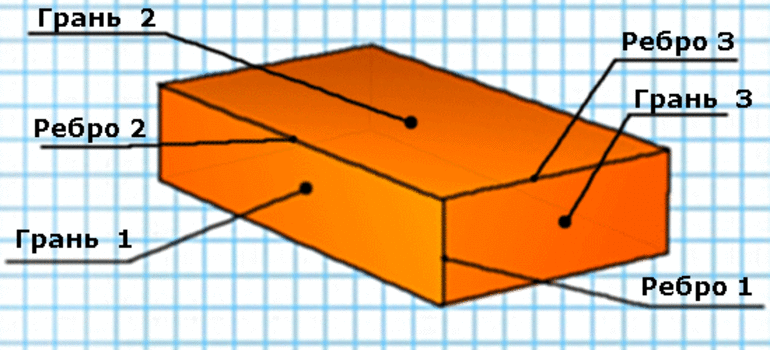
Прямоугольники, которые составляют поверхность параллелепипеда, являются гранями параллелепипеда.

Прямоугольный параллелепипед определяют 3-мя измерениями:

Высота (обозначают как h) равняется длине ребра № 1.

Длина (обозначают как m) равняется длине ребра № 2.

Ширина (обозначают как n) равняется длине ребра № 3.

Площадь всей поверхности параллелепипеда обозначают как S:

В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трех его измерений.

Прямоугольный параллелепипед

Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.

Свойства прямоугольного параллелепипеда:

1. В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
2. Противоположные грани попарно равны и параллельны.
3. Все двугранные углы прямоугольного параллелепипеда – прямые.
4. Диагонали прямоугольного параллелепипеда равны.
5. Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

$с$ — высота(она же боковое ребро);

$P_$ — периметр основания;

$S_$ — площадь основания;

$S_$ — площадь боковой поверхности;

$S_$ — площадь полной поверхности;

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

$S_=P_·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.

Дополнительные сведения, которые пригодятся для решения задач:

$а$ — длина стороны.

$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.

Пирамида

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Объем любой пирамиды равен трети произведения основания и высоты.

В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.

В основании лежит треугольник.

• $S=/$, где $h_a$ — высота, проведенная к стороне $а$.
• $S=/$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
• Формула Герона $S=√

  $, где $р$ — это полупериметр $p=/$.

• $S=p·r$, где $r$ — радиус вписанной окружности.
• $S=/$, где $R$ — радиус описанной окружности.
• Для прямоугольного треугольника $S=/$, где $а$ и $b$ — катеты прямоугольного треугольника.
• Для равностороннего треугольника $S=/$, где $а$ — длина стороны.

В основании лежит четырехугольник.

1. Прямоугольник.
   $S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб.
   $S=/$, где $d_1$ и $d_2$ — диагонали ромба.
   $S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
3. Трапеция.
   $S=/$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
4. Квадрат.
   $S=a^2$, где $а$ — сторона квадрата.

Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.

Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.

Объем пирамиды, в основании которой лежит прямоугольник

Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.

В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.

Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Измерения прямоугольного параллелепипеда и его свойства

Что такое прямоугольный параллелепипед — определение

Параллелепипед — это призма с шестью гранями, в основании которой лежит параллелограмм.

Согласно другому определению, это многогранник, состоящий из шести сторон-параллелограммов.

В математике в целом, и в геометрии в частности, выделяют несколько основных видов параллелепипеда:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

• прямоугольный;
• прямой — параллелепипед, у которого 4 боковые грани являются прямоугольниками;
• наклонный — боковые грани объемной фигуры не перпендикулярны основаниям;
• ромбоэдр — шестигранная призма, грани которой — это ромбы;
• куб — состоит из квадратных граней.

Прямоугольный параллелепипед — это шестигранная призма, каждая из сторон которой в общем случае является прямоугольником. Также это — многогранник, в основании которого лежит прямоугольник, а боковые грани перпендикулярны основанию.

Прямоугольных параллелепипедов в окружающем человека мире множество: комната, закрытая книга, системный блок компьютера, закрытая коробка для подарка, спичечный коробок и т. д.

Прямоугольный параллелепипед, как и любой другой, состоит из:

• основания;
• граней — противоположных, т. е. не имеющих общего ребра, и смежных — тех, которые имеют общее ребро;
• ребер — отрезков, соединяющих соседние вершины объемной шестигранной фигуры;
• диагоналей — отрезков, соединяющих противоположные вершины;
• диагоналей граней;
• высоты — отрезка, соединяющего верхнее и нижнее основания шестигранной призмы.

В некоторых базовых задачах просят найти количество составляющих элементов шестигранной призмы. Эти числа можно запомнить: объемная фигура состоит из 8 вершин, 12 ребер и 6 граней.

Измерениями прямоугольного параллелепипеда называют его длину, ширину и высоту.

Свойства параллелепипеда, какими обладают противолежащие грани

Вне зависимости от вида параллелепипеда, все они обладают 4 свойствами:

1. Противолежащие грани равны друг другу и попарно параллельны.
2. Все 4 диагонали шестигранника пересекаются в одной точке, которой делятся пополам. Любой отрезок, проходящий через середину диагонали, и концы которого принадлежат поверхности, также делится пополам.
3. Фигура симметрична относительно середины диагонали.
4. Квадрат длины диагонали равен сумме квадратов трех измерений.

Прямоугольный параллелепипед обладает всеми этими свойствами и несколькими специфичными, свойственными только ему.

1. Все стороны — прямоугольники.
2. Все углы, состоящие из двух граней, равны 90°.
3. Любую сторону можно принять за основание.
4. Если все ребра равны и перпендикулярны, то такой шестигранник считается кубом.

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда

Объем прямоугольного параллелепипеда равен длине, умноженной на ширину и высоту.

где V — объем, a — длина, b — ширина, h — высота.

Площадь боковой поверхности равна сумме площадей боковых граней.

Площадь полной поверхности равна сумме площадей боковых граней и оснований.

Как найти диагональ и ширину прямоугольного параллелепипеда

В соответствии с одним из основных свойств параллелепипеда, квадрат длины диагонали равен сумме квадратов трех измерений. Запишем в виде формулы:

Следовательно, длина диагонали равна квадратному корню из суммы трех измерений фигуры:

Длина, ширина и высота, как правило, вычисляются через формулу объема:

Существует и второй вариант, как возможно найти одно из измерений. Если известно смежное ему измерение и диагональ общей стороны шестигранника, то можно вычислить вторую сторону через теорему Пифагора или по свойствам диагонали.